可视化图解算法60:矩阵最长递增路径
原创可视化图解算法60:矩阵最长递增路径
原创用户11589437
发布于 2025-09-11 16:57:58
发布于 2025-09-11 16:57:58
牛客网 面试笔试 TOP101
可视化图解算法60:矩阵最长递增路径
1. 题目
描述
给定一个 n 行 m 列矩阵 matrix ,矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径,使这条路径上的元素是递增的。并输出这条最长路径的长度。
这个路径必须满足以下条件:
- 对于每个单元格,你可以往上,下,左,右四个方向移动。 你不能在对角线方向上移动或移动到边界外。
- 你不能走重复的单元格。即每个格子最多只能走一次。
数据范围:1≤n,m≤1000,0 ≤matrix [i] [j]≤1000
进阶:空间复杂度 O(nm) ,时间复杂度 O(nm)
例如:当输入为[[1,2,3],[4,5,6],[7,8,9]]时,对应的输出为5,
其中的一条最长递增路径如下图所示:

示例1
输入:
[[1,2,3],[4,5,6],[7,8,9]]
返回值:
5
说明:
1->2->3->6->9即可。当然这种递增路径不是唯一的。
示例2
输入:
[[1,2],[4,3]]
返回值:
4
说明:
1->2->3->4
备注:
矩阵的长和宽均不大于1000,矩阵内每个数不大于1000
2. 解题思路
首先,我们需要明确题目的要求:
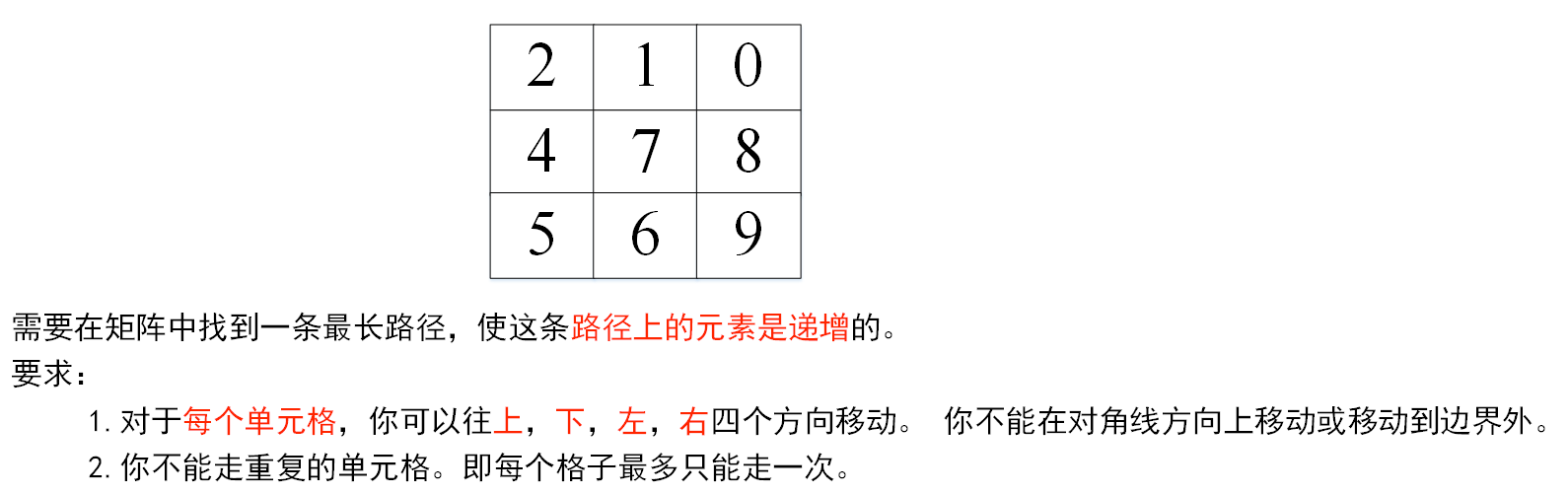
对应的思路如下:
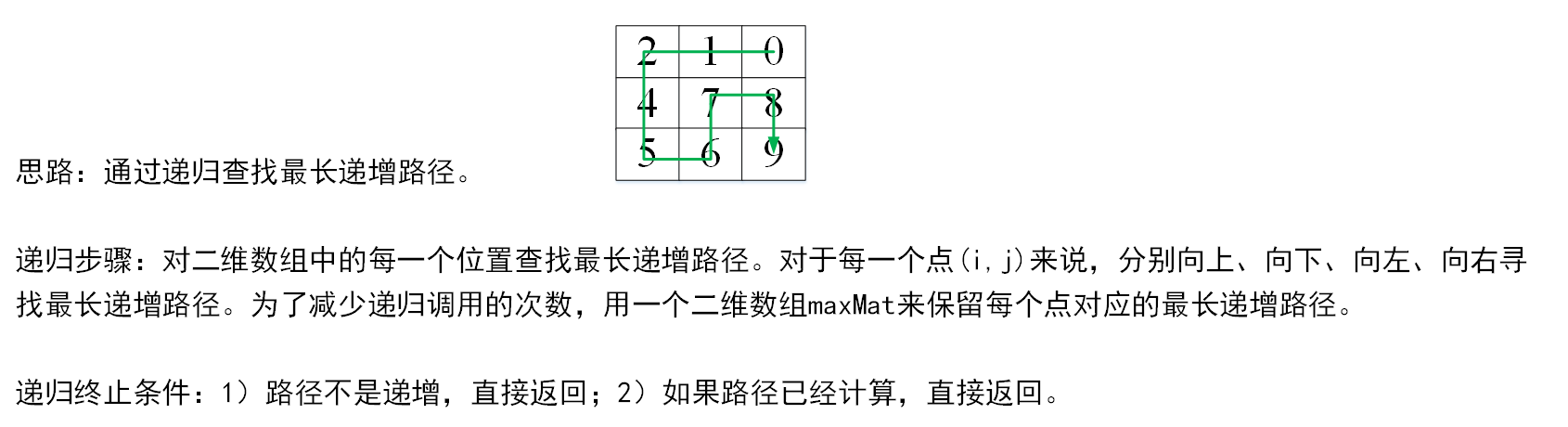
如果文字描述的不太清楚,你可以参考视频的详细讲解:B站@好易学数据结构
3. 编码实现
核心代码如下:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 递增路径的最大长度
* @param matrix int整型二维数组 描述矩阵的每个数
* @return int整型
*/
func solve(matrix [][]int) int {
// write code here
maxMat = newArray(len(matrix), len(matrix[0]))
maxValue := 0 //最长路径
for i := 0; i < len(matrix); i++ {
for j := 0; j < len(matrix[i]); j++ {
//二维数组中的每一个点都可能是最大路径的起始点
preMax := dfs(matrix, i, j, -1)
maxValue = max(maxValue, preMax)
}
}
return maxValue
}
var (
// 如果我们已经知道以该点为头的最长递增路径长度,那么在dfs查找时可以直接使用这个长度,而无需再次计算.
// 用一个矩阵将已经计算得到的最长递增路径进行存储
maxMat [][]int
)
// 以坐标(i,j)为起始点的最长路径
func dfs(mat [][]int, i int, j int, pre int) int {
//2.递归终止条件:不是递增,直接返回
if mat[i][j] <= pre {
return 0
}
//3.剪枝:如果该点已经计算过,直接返回,不用再重新计算
if maxMat[i][j] != 0 {
return maxMat[i][j]
}
maxVal := 0
// 1. 递归步骤
//1.1 向左
if i > 0 {
//用 mat[i][j] 作为 pre,去比较其左侧的数据
perMax := dfs(mat, i-1, j, mat[i][j])
maxVal = max(maxVal, perMax)
}
//1.2 向右
if i < len(mat)-1 {
//用 mat[i][j] 作为 pre,去比较其右侧的数据
perMax := dfs(mat, i+1, j, mat[i][j])
maxVal = max(maxVal, perMax)
}
//1.3 向上
if j > 0 {
//用 mat[i][j] 作为 pre,去比较其上侧的数据
perMax := dfs(mat, i, j-1, mat[i][j])
maxVal = max(maxVal, perMax)
}
//1.4 向下
if j < len(mat[i])-1 {
//用 mat[i][j] 作为 pre,去比较其下侧的数据
perMax := dfs(mat, i, j+1, mat[i][j])
maxVal = max(maxVal, perMax)
}
maxMat[i][j] = maxVal + 1 //最长路径:上下左右最长的路径+1(当前的点)
return maxMat[i][j]
}
func max(a, b int) int {
if a >= b {
return a
}
return b
}
func newArray(row, column int) [][]int {
arr := make([][]int, row)
for i := 0; i < row; i++ {
arr[i] = make([]int, column)
}
return arr
}具体完整代码你可以参考下面视频的详细讲解。
- Python编码:B站@好易学数据结构
- Java编码:B站@好易学数据结构
- Golang编码:B站@好易学数据结构
4.小结
矩阵的最长递增路径通过遍历+递归的思想完成。对二维数组中的每一个位置查找最长递增路径。对于每一个点(i,j)来说,分别向上、向下、向左、向右寻找最长递增路径。为了减少递归调用的次数,用一个二维数组maxMat来保留每个点对应的最长递增路径。

《数据结构与算法》深度精讲课程正式上线啦!7 大核心算法模块全解析:
✅ 链表
✅ 二叉树
✅ 二分查找、排序
✅ 堆、栈、队列
✅ 回溯算法
✅ 哈希算法
✅ 动态规划
无论你是备战笔试面试、提升代码效率,还是突破技术瓶颈,这套课程都将为你构建扎实的算法思维底座。🔥立即加入学习打卡,与千名开发者共同进阶!
- Python编码实现:B站@好易学数据结构
- Java编码实现:B站@好易学数据结构
- Golang编码实现:B站@好易学数据结构
对于LeetCode数据结构与算法,我们总结了一套【可视化+图解】方法,依据此方法来解决相关问题,算法变得易于理解,写出来的代码可读性高也不容易出错。具体也可以参考视频详细讲解。
今日佳句:奇文共欣赏,疑义相与析。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
评论
登录后参与评论
推荐阅读
目录

