《算法闯关指南：优选算法--二分查找》--17.二分查找(附二分查找算法简介)，18. 在排序数组中查找元素的第一个和最后一个位置

🔥草莓熊Lotso：个人主页

❄️个人专栏：《C++知识分享》《Linux 入门到实践：零基础也能懂》

✨生活是默默的坚持，毅力是永久的享受。

🎬博主简介：

前言：

聚焦算法题实战，系统讲解三大核心板块：优选算法：剖析动态规划、二分法等高效策略，学会寻找“最优解”。 递归与回溯：掌握问题分解与状态回退，攻克组合、排列等难题。 贪心算法：理解“局部最优”到“全局最优”的思路，解决区间调度等问题 内容以题带点，讲解思路与代码实现，帮助大家快速提升代码能力。

二分查找算法简介：

二分查找（Binary Search），也称为折半查找，是一种高效的有序数组查找算法。其核心思想是通过不断将搜索区间减半，快速缩小目标值的可能范围，最终找到目标值或确定其不存在。该算法的时间复杂度为 O(log n)，远优于顺序查找的 O (n)，在处理大规模有序数据时优势显著

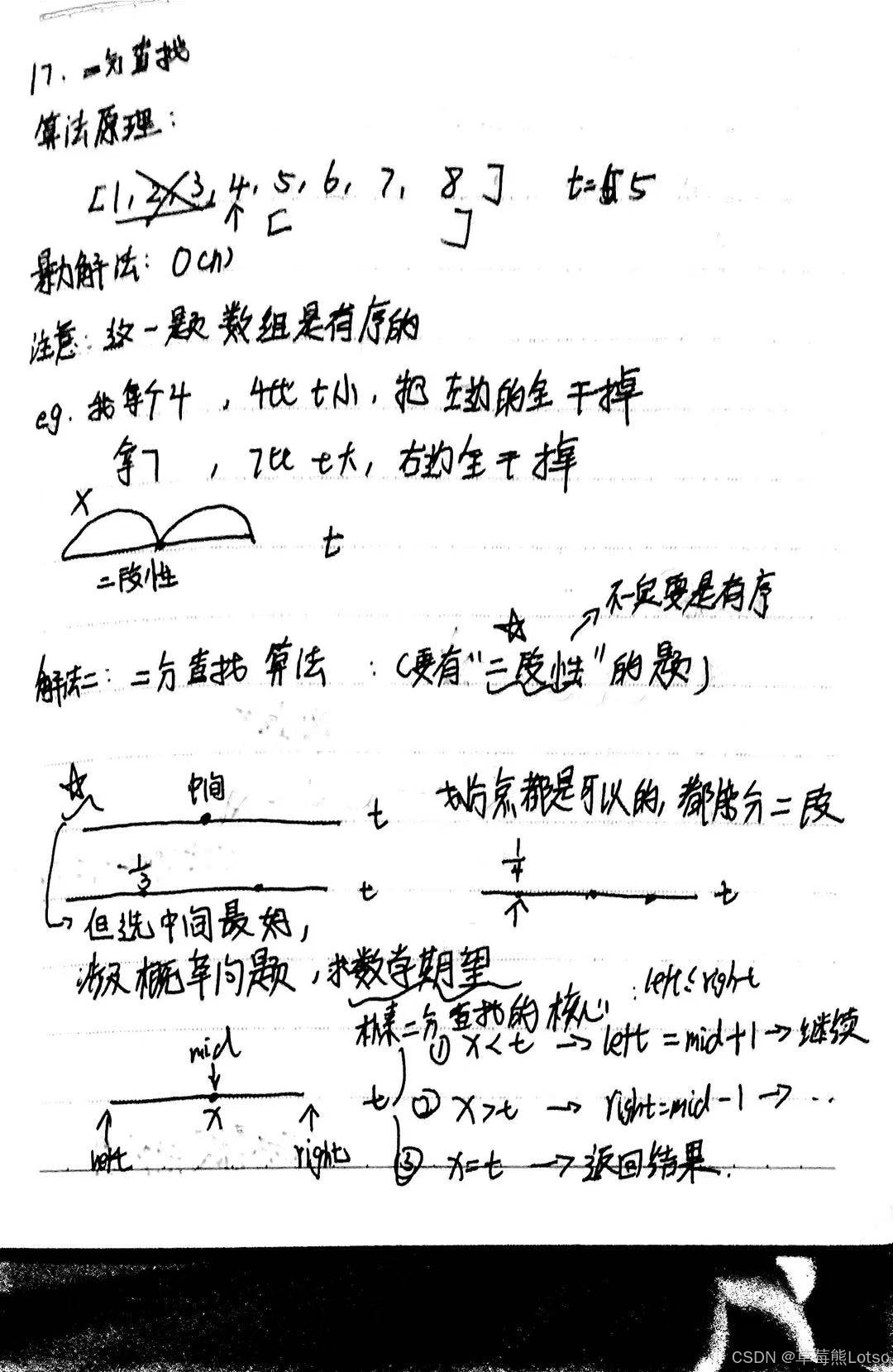
17. 二分查找

题目链接：

704. 二分查找 - 力扣（LeetCode）

题目描述：

题目示例：

解法：

算法流程：

定义 left，right指针，分别指向数组的左右区间。

找到待查找区间的中间点 mid ，找到之后分三种情况讨论：

• arr[mid]==target 说明正好找到，返回 mid 的值；
• arr[mid]>target 说明 [mid，right] 这段区间都是大于 target 的。因此舍去右边区间，往左边[left，mid-1] 的区间继续查找，既让 right=mid-1，然后重复 2 过程
• arr[mid]<target 说明[left，mid]这段区间的值都是小于 target 的。因此舍去左边区间，在右边][mid+1，right] 区间继续查找，即让 left=mid-1，然后重复 2 过程

当 left 与 right 错开时，说明整个区间都没有这个数，返回 -1；

C++算法代码：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+(right-left)/2;//防止数据溢出
            if(nums[mid]<target) left=mid+1;
            else if(nums[mid]>target) right=mid-1;
            else return mid;
        }
        return -1;
    }
};

朴素二分查找算法模板：

        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+(right-left)/2;//防止数据溢出
            if(……………………) 
                    left=mid+1;
            else if(…………………………)
                     right=mid-1;
            else return …………………………;
        }

算法总结&&笔记展示：

笔记字有点丑，大家见谅：

18. 在排序数组中查找元素的第一个和最后一个位置

题目链接：

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

题目描述：

题目示例：

解法：

算法思路：

用的还是二分思想，就是根据数据的性质，在某种判断条件下将区间一分为二，然后舍去其中一个区间，然后再另一个区间内查找；

方便叙述，用 x 表示该元素，resleft 表示左边界，resright 表示右边界。

寻找左边界思路：

寻找左边界：我们需要注意到以左边界划分的两个区间的特点

• 左边区间 [left, resLeft - 1] 都是小于 x 的；
• 右边区间（包括左边界） [resLeft, right] 都是大于等于 x 的；

因此，关于 mid 的落点，我们可以分为下面两种情况：

• 当我们的 mid 落在 [left, resLeft - 1] 区间的时候，也就是 arr[mid] < target 。说明 [left, mid] 都是可以舍去的，此时更新 left 到 mid + 1 的位置， 继续在 [mid + 1, right] 上寻找左边界；
• 当 mid 落在 [resLeft， right] 的区间的时候，也就是 arr[mid] >= target 。 说明 [mid + 1, right] （因为 mid 可能是最终结果，不能舍去）是可以舍去的，此时更新 right 到 mid 的位置，继续在 [left, mid] 上寻找左边界；

由此，就可以通过⼆分，来快速寻找左边界；

注意：这里找中间元素需要向下取整。

因为后续移动左右指针的时候：

• 左指针： left = mid + 1 ，是会向后移动的，因此区间是会缩小的；
• 右指针： right = mid ，可能会原地踏步（比如：如果向上取整的话，如果剩下 1,2 两个元素， left == 1 ， right == 2 ， mid == 2 。更新区间之后， left，right，mid 的值没有改变，就会陷入死循环）。

因此⼀定要注意，当 right = mid 的时候，要向下取整。

寻找右边界思路：

寻右右边界： 用resRight 表示 右边界， 我们注意到右边界的特点：

• 左边区间 （包括右边界） [left, resRight] 都是小于等于 x 的；
• 右边区间 [resRight+ 1, right] 都是大于 x 的；

因此，关于 mid 的落点，我们可以分为下面两种情况：

• 当我们的 mid 落在 [left, resRight] 区间的时候，说明 [left, mid - 1] （ mid 不可以舍去，因为有可能是最终结果） 都是可以舍去的，此时更新 left 到 mid的位置；
• 当 mid 落在 [resRight+ 1, right] 的区间的时候，说明 [mid, right] 内的元素是可以舍去的，此时更新 right 到 mid - 1 的位置；

由此，就可以通过⼆分，来快速寻找右边界；

注意：这里找中间元素需要向上取整。

因为后续移动左右指针的时候：

• 左指针： left = mid ，可能会原地踏步（比如：如果向下取整的话，如果剩下 1,2 两个元素， left == 1， right == 2，mid == 1 。更新区间之后， left，right，mid 的值没有改变，就会陷入死循环）。
• 右指针： right = mid - 1 ，是会向前移动的，因此区间是会缩小的；

因此⼀定要注意，当 right = mid 的时候，要向下取整。

C++算法代码：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int begin=0,end=0,mid=0;
        if (nums.empty()) 
        {
            return {-1, -1};
        }
        //1.查找区间左端点
        int left=0,right=nums.size()-1;
        while(left<right)
        {
           mid=left+(right-left)/2;
            if(nums[mid]<target) left=mid+1;
            else right=mid;
        }
        if(nums[left]==target) begin=left;
        else return{-1,-1};

        //2.查找区间右端点
         left=0,right=nums.size()-1;
         while(left<right)
         {
            mid=left+(right-left+1)/2;
            if(nums[mid]<=target) left=mid;
            else right=mid-1;
         }
         if(nums[right]==target) end=right;
         else return{-1,-1};

         return{begin,end};
    }
};

算法总结&&笔记展示：

笔记字有点丑，大家见谅：

二分查找算法总结：

请大家⼀定不要觉得背下模板就能解决所有⼆分问题。⼆分问题最重要的就是要分析题意，然后定

要搜索的区间，根据分析问题来写出二分查找算法的代码。 要分析题意，确定搜索区间，不要死记模板，不要看左闭右开什么乱七⼋糟的题解

模板记忆技巧：

• 关于什么时候用三段式，还是二段式中的某⼀个，⼀定不要强行去用，而是通过具体的问题分析情况，根据查找区间的变化确定指针的转移过程，从⽽选择⼀个模板。
• 当选择两段式的模板时： 在求 mid 的时候，只有 right - 1 的情况下，才会向上取整（也就是 +1 取中间数）

结尾：

往期回顾：

《算法闯关指南：优选算法--滑动窗口》--15.串联所有单词的子串，16.最小覆盖子串

结语：本文系统讲解了二分查找算法及其应用。首先介绍了二分查找的基本原理，即通过不断对半缩小搜索范围，在有序数组中高效查找元素，时间复杂度为O(logn)。接着以LeetCode 704题为例，详细解析了标准二分查找的实现步骤和代码模板。然后进阶讲解了34题中查找元素边界位置的二分变种，重点分析了左边界和右边界查找的不同策略及注意事项，包括mid取整方式的差异。

✨把这些内容吃透超牛的！放松下吧✨ ʕ˘ᴥ˘ʔ づきらど