【数据结构与算法】数据结构初阶：详解二叉树（二）——堆

艾莉丝努力练剑

发布于 2025-11-12 19:02:11

220

文章被收录于专栏：C / C++C / C++

重要提醒：为什么我们要学那么多的数据结构？这是因为没有一种数据结构能够去应对所有场景。我们在不同的场景需要选择不同的数据结构，所以数据结构没有谁好谁坏之分，而评估数据结构的好坏要针对场景，如果在一种场景下我们需要频繁地对头部进行插入删除操作，那么这个时候我们用链表；但是如果对尾部进行插入删除操作比较频繁，那我们用顺序表比较好。因此，不同的场景我们选择不同的数据结构。

前言：本篇文章，我们继续来看二叉树相关的知识点，在初阶的数据结构与算法阶段，我们把知识点分成三部分，复杂度作为第一部分，顺序表和链表、栈和队列、二叉树为第二部分，排序为第二部分，我们之前已经介绍完了第一部分：算法复杂度，本文我们将正式开始学习第二部分中的二叉树部分内容啦。注意，二叉树的学习需要一定的基础，涉及到【函数栈帧的创建与销毁】，而且二叉树尤其是链式结构二叉树基本上是递归算法的暴力美学。

链接：【深入详解】函数栈帧的创建与销毁：寄存器、压栈、出栈、调用、回收空间

正文

三、二叉树的顺序结构：堆

（一）堆——顺序结构

1、堆的概念

根节点最大的堆就叫最大堆（大根堆），根节点最小的堆就叫最小堆（小根堆）。

下面是小根堆和大根堆的图片示例：

小根堆：

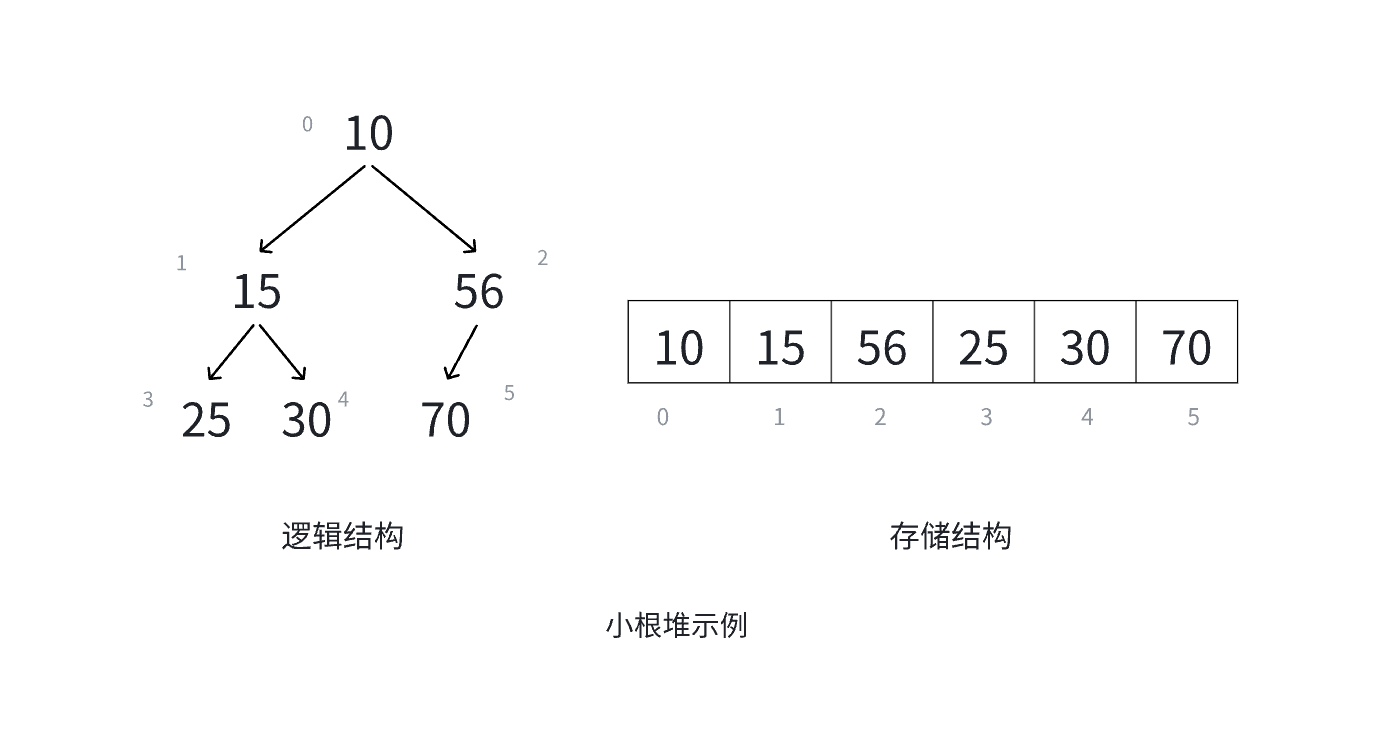
大根堆：

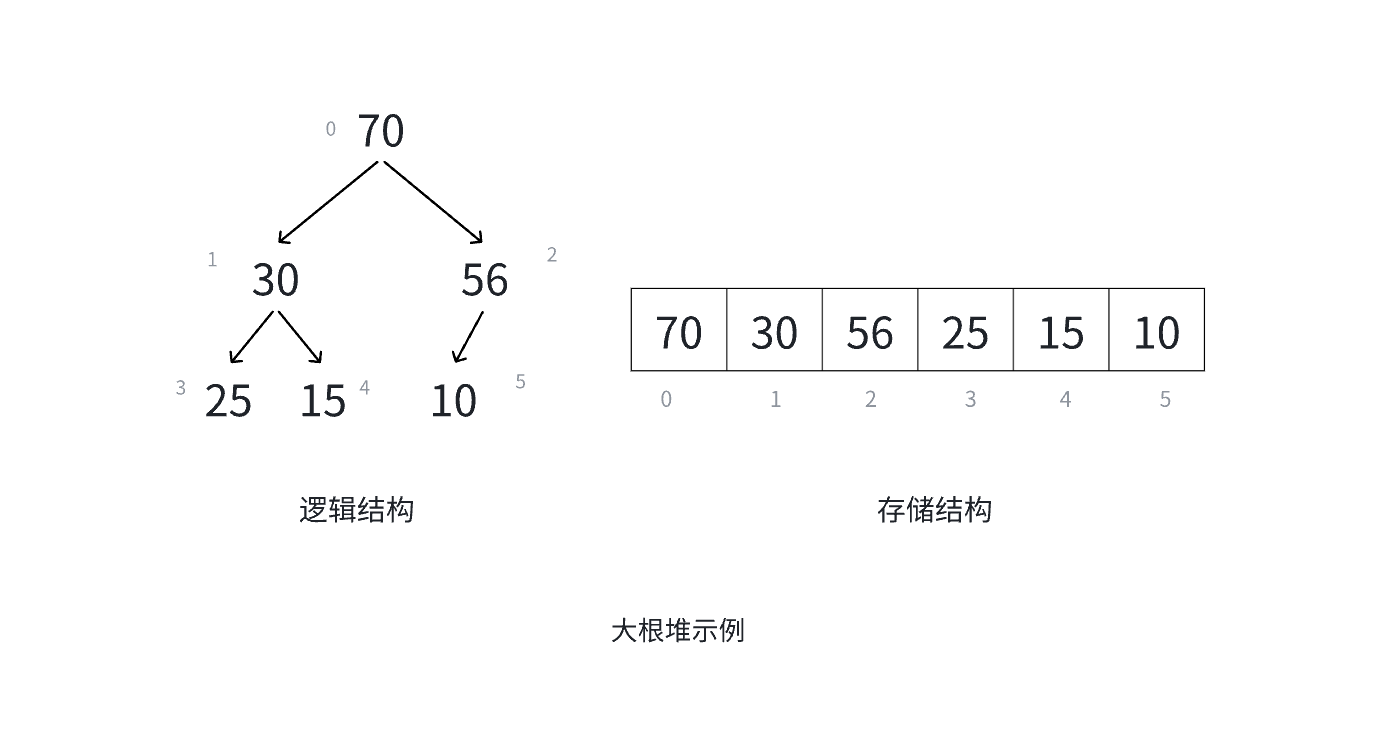
2、堆的性质

性质：

1、堆是一种完全二叉树； 2、堆中某个结点的值总是不大于或不小于其父结点的值。

二叉树性质：

对于具有 n 个结点的完全二叉树，如果按照从上到下、从左到右的数组顺序对所有结点从 0 开始编号，则对于序号为 i 的结点有：

1.若 i > 0，i位置结点的双亲序号： (i - 1)/2 ； i = 0 ，i 为根结点编号，无双亲结点； 2.若2i +1，左孩子序号： 2i + 1，2i + 1 >= n否则没有左孩子； 3.若2i+2，右孩子序号：2i+2，2i + 2 >= n否则没有右孩子。

（二）堆结构各种方法的实现

1、各种方法的实现

（1）堆结构的定义

Heap.h：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

//定义堆结构
typedef int HPDatatype;
typedef struct Heap {
	HPDatatype* arr;
	int size;//有效数据个数
	int capacity;//空间大小
}HP;

（2）初始化

Heap.c：

//初始化
void HPInit(HP* php)
{
	//断言，不能传NULL，为了提高代码的健壮性
	assert(php);

	php->arr = NULL;
	php->capacity = php->size = 0;
}

test.c：

#include"Heap.h"

void test01()
{
	HP hp;
	HPInit(&hp);
}

int main()
{
	test01();
	return 0;
}

（3）销毁

Heap.c：

//销毁
void HPDestory(HP* php)
{
	assert(php);
	if (php)
		frree(php->arr);
	php->arr = NULL;//堆的底层就是数组
	php->size = php->capacity = 0;
}

test.c：

#include"Heap.h"

void test01()
{
	HP hp;
	HPInit(&hp);

    HPDesTroy(&hp);
}

int main()
{
	test01();
	return 0;
}

（4）打印

Heap.c：

void HPPrint(HP* php)
{
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->arr[i]);
	}
	printf("\n");
}

（5）交换——Swap方法

Heap.c：

void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

（6）向上调整算法

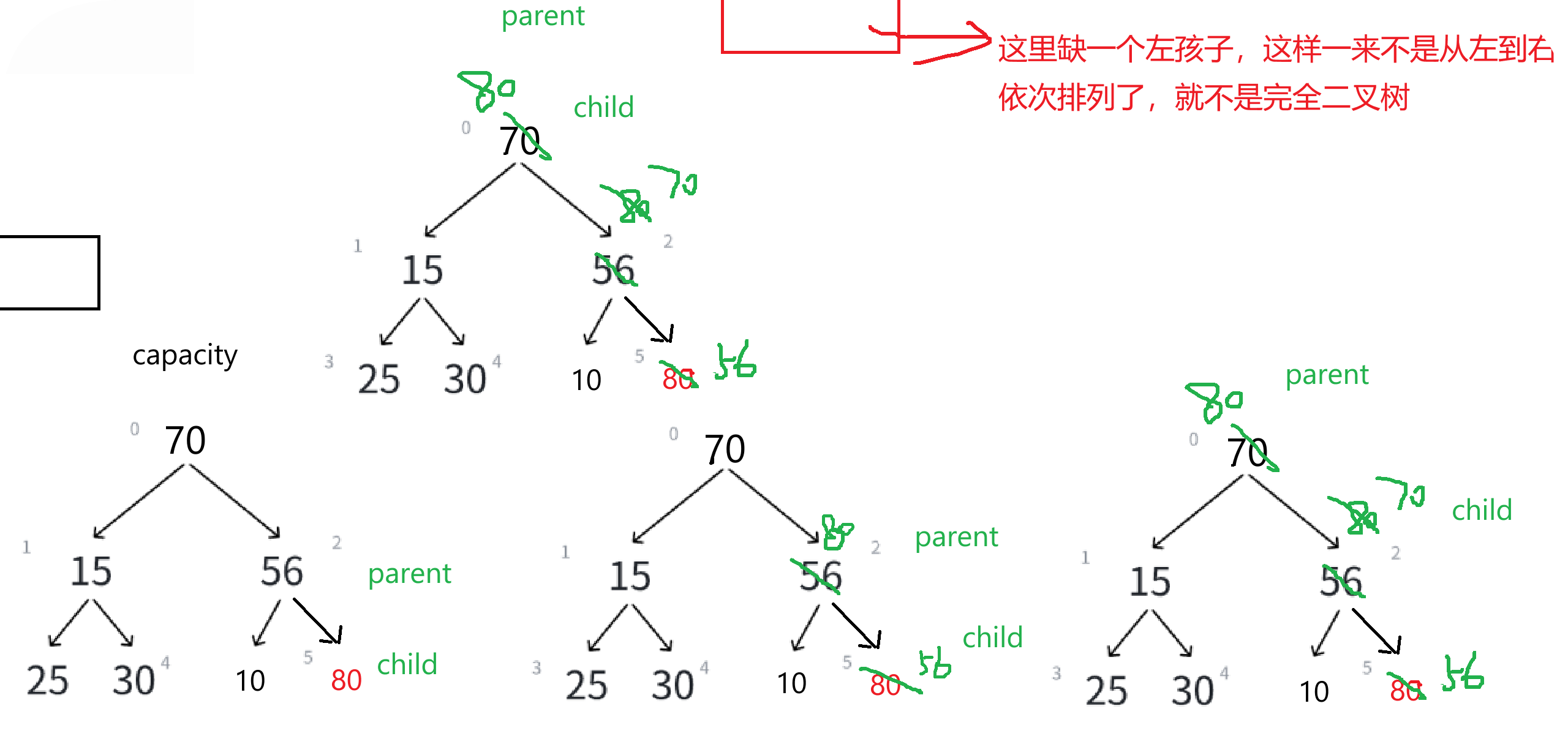
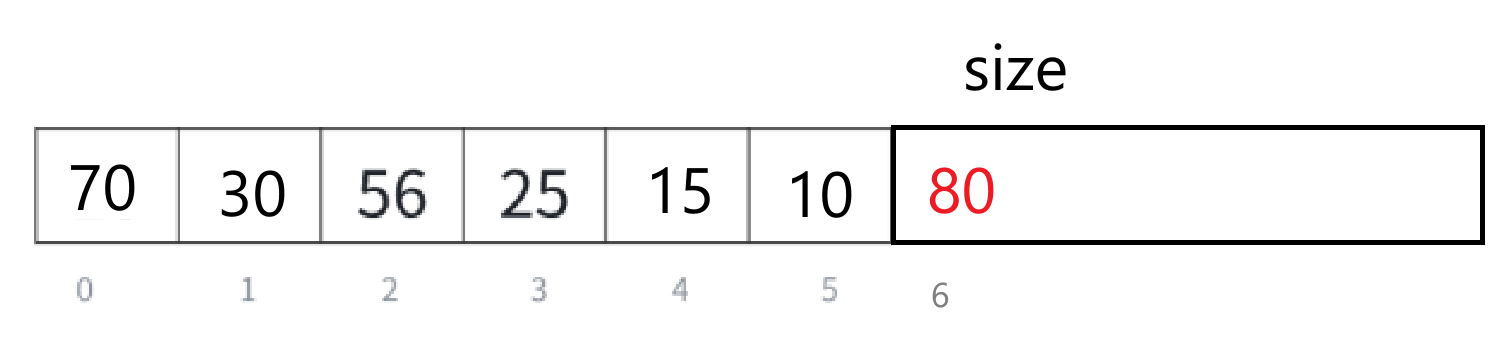
如果存储结构修改一下，改成这样——

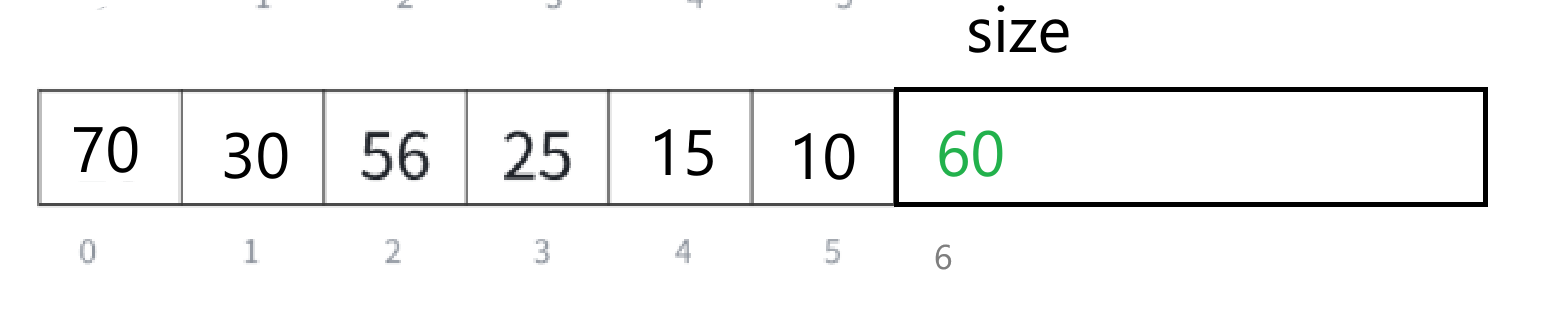
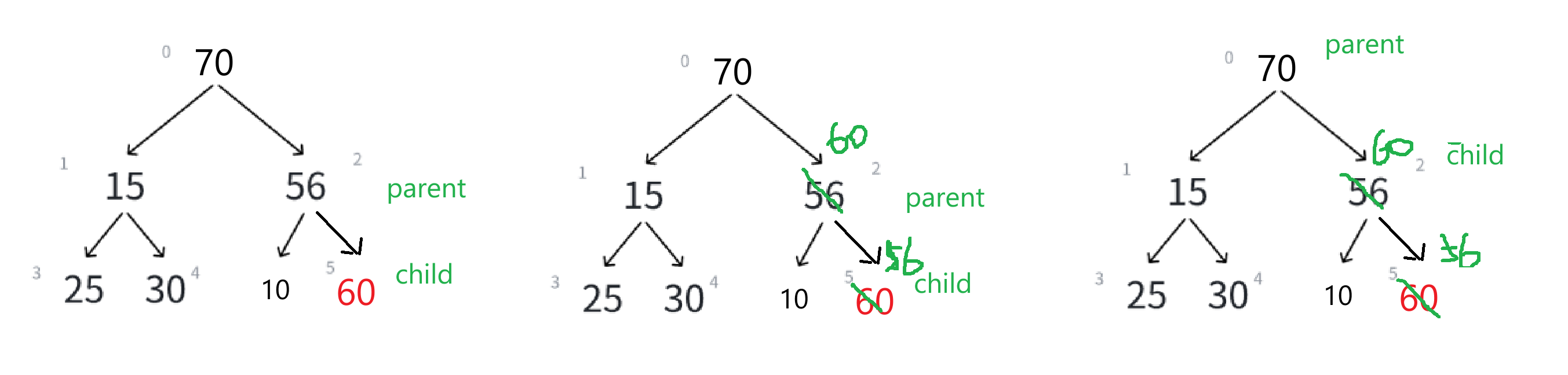
我们理解清楚向上调整之后，就来写一个向上调整算法的代码——

Heap.c：

//向上调整算法
void AdjustUp(HPDataType* arr, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//建大堆：>
		//建小堆: <
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else {
			break;
		}
	}
}

（7）向下调整算法

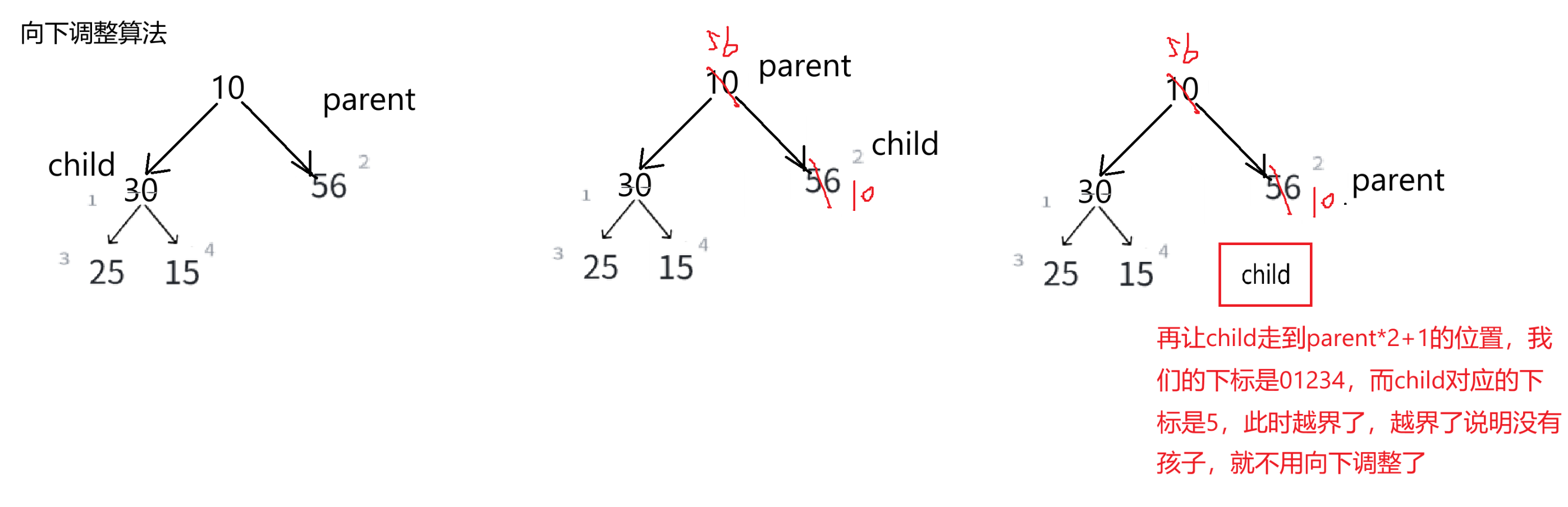
再让child走到parent*2+1的位置，我们的下标是01234，而child对应的下标是5，此时越界了，越界了说明没有孩子，就不用向下调整了
再举一个大根堆的例子——

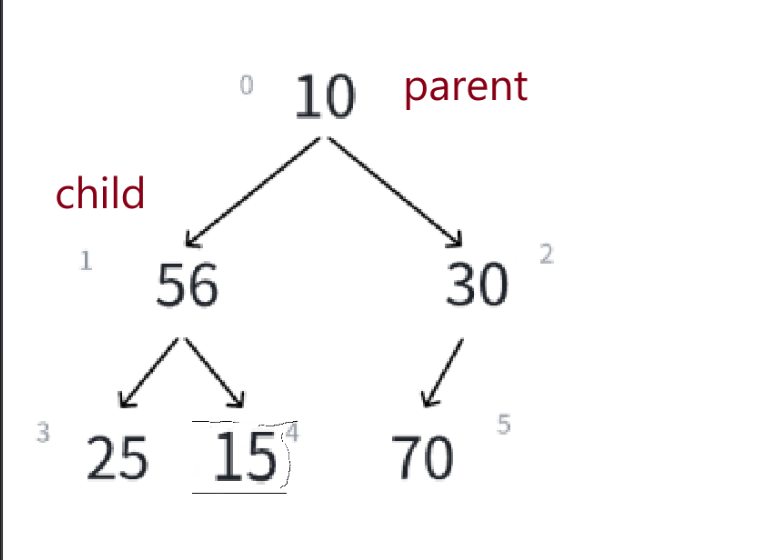
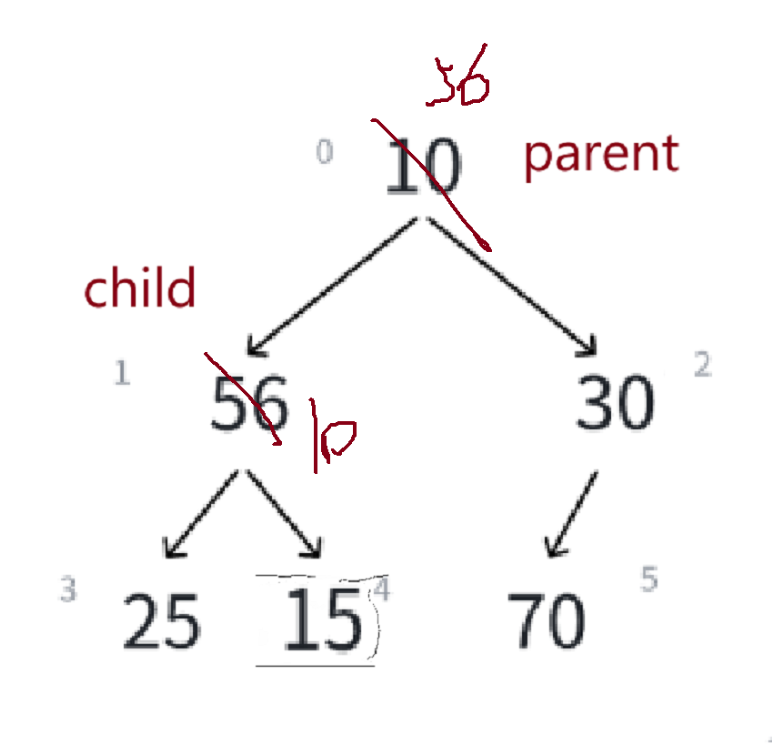
每次交换完，child = parent*2+1，parent挪到child的位置，比较左右孩子，左孩子大，child位置不动，比较子与父大小，大的往上放——

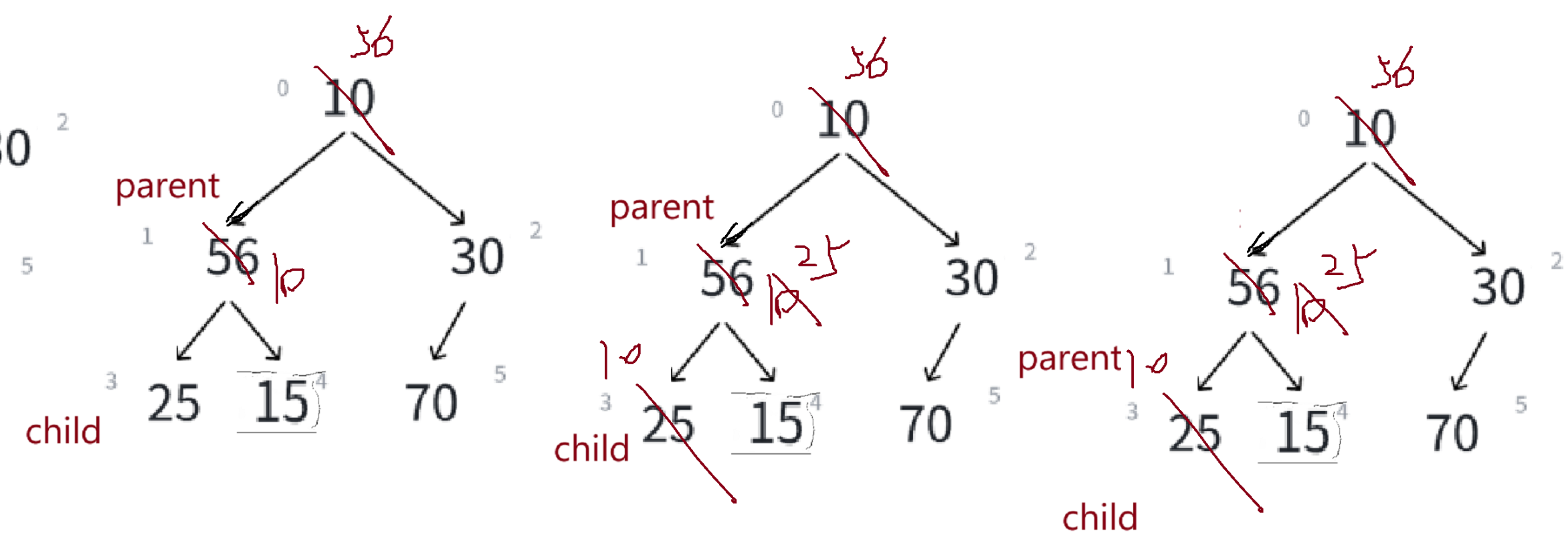
		//找最大的孩子
		if (arr[child] < arr[child + 1]);
		{
			child++;
		}

这个代码感觉有问题吗？

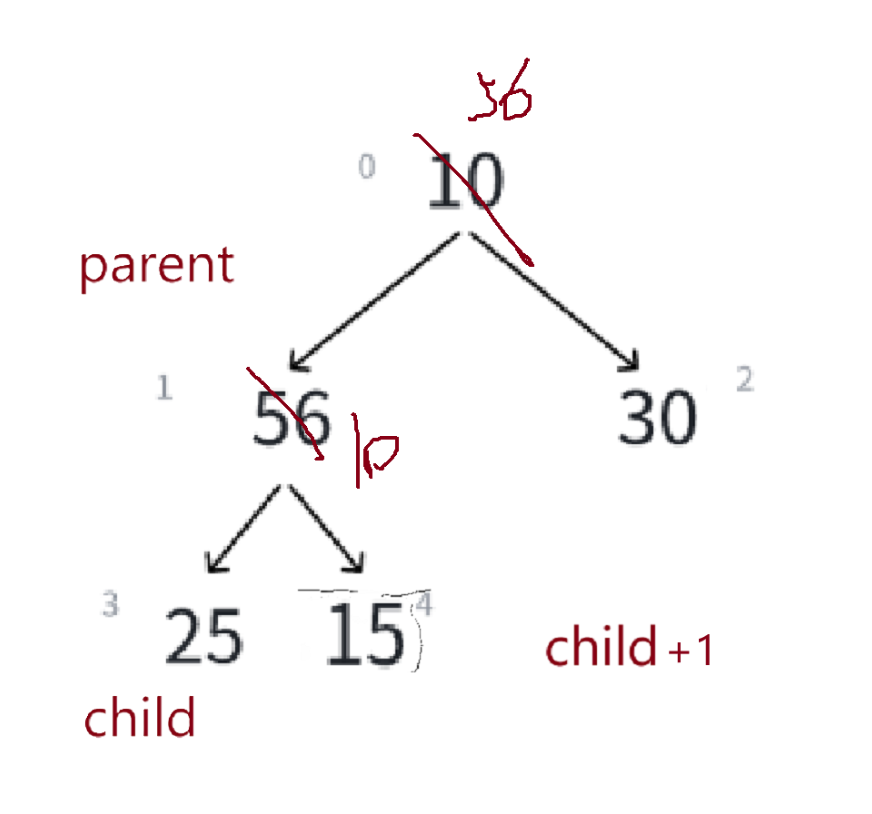
child+1可能越界了，我们改一下——

		//找最大的孩子
		if (child + 1 < n && arr[child] < arr[child + 1]);
		{
			child++;
		}

这样我们便修复了一个BUG！

Heap.c：

//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//建大堆：<
		//建小堆: >
		if (child + 1 < n && arr[child] > arr[child + 1])
		{
			child++;
		}
		//孩子和父亲比较
		//建大堆：>
		//建小堆:<
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else {
			break;
		}
	}
}

（8）入堆——数据插入

Heap.c：

void HPPush(HP* php, HPDataType x)
{
	assert(php);
	//空间不够要增容
	if (php->size == php->capaicty)
	{
		//增容
		int newCapacity = php->capaicty == 0 ? 4 : 2 * php->capaicty;
		HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapacity * sizeof(HPDataType));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);
		}
		php->arr = tmp;
		php->capaicty = newCapacity;
	}
	//空间足够
	php->arr[php->size] = x;
	//向上调整
	AdjustUp(php->arr, php->size);
	++php->size;
}

test.c：

#include"Heap.h"

void test01()
{
	HP hp;
	HPInit(&hp);
	HPPush(&hp, 25);
	HPPush(&hp, 15);
	HPPush(&hp, 10);
	HPPush(&hp, 56);
	HPPush(&hp, 70);
	HPPush(&hp, 30);
	HPPrint(&hp);

	HPDesTroy(&hp);
}

int main()
{
	test01();
	return 0;
}

（9）判断是否为空

Heap.c：

bool HPEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

（10）出堆——数据删除

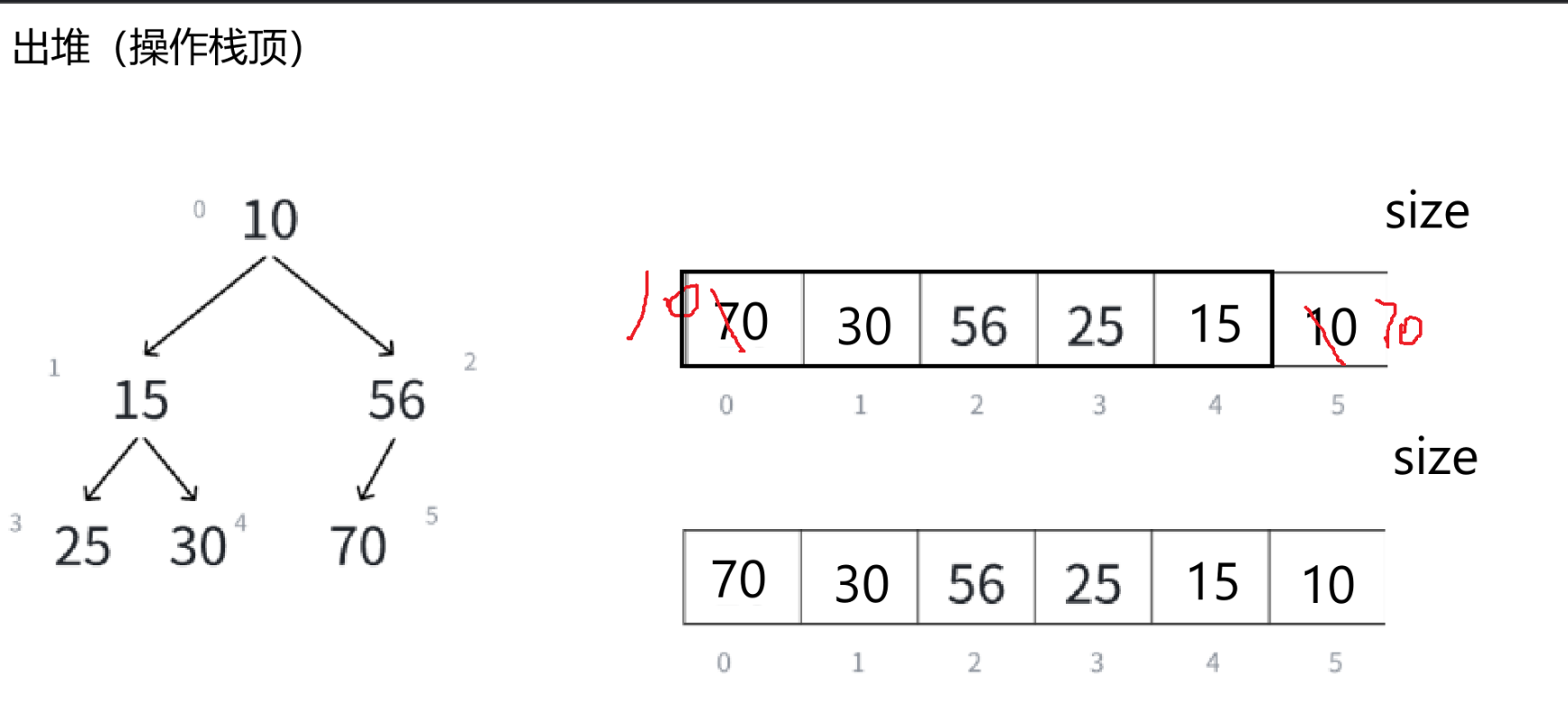
Heap.c：

void HPPop(HP* php)
{
	assert(!HPEmpty(php));
	Swap(&php->arr[0], &php->arr[php->size - 1]);
	--php->size;
	//堆顶数据需要向下调整
	AdjustDown(php->arr, 0, php->size);
}

test.c：

#include"Heap.h"

void test01()
{
	HP hp;
	HPInit(&hp);
	HPPush(&hp, 25);
	HPPush(&hp, 15);
	HPPush(&hp, 10);
	HPPush(&hp, 56);
	HPPush(&hp, 70);
	HPPush(&hp, 30);
	HPPrint(&hp);

	HPPop(&hp);
	HPPrint(&hp);
	HPPop(&hp);
	HPPrint(&hp);
	HPPop(&hp);
	HPPrint(&hp);
	HPPop(&hp);
	HPPrint(&hp);
	HPPop(&hp);
	HPPrint(&hp);

	HPDesTroy(&hp);
}
int main()
{
	test01();
	return 0;
}

先删除一次——

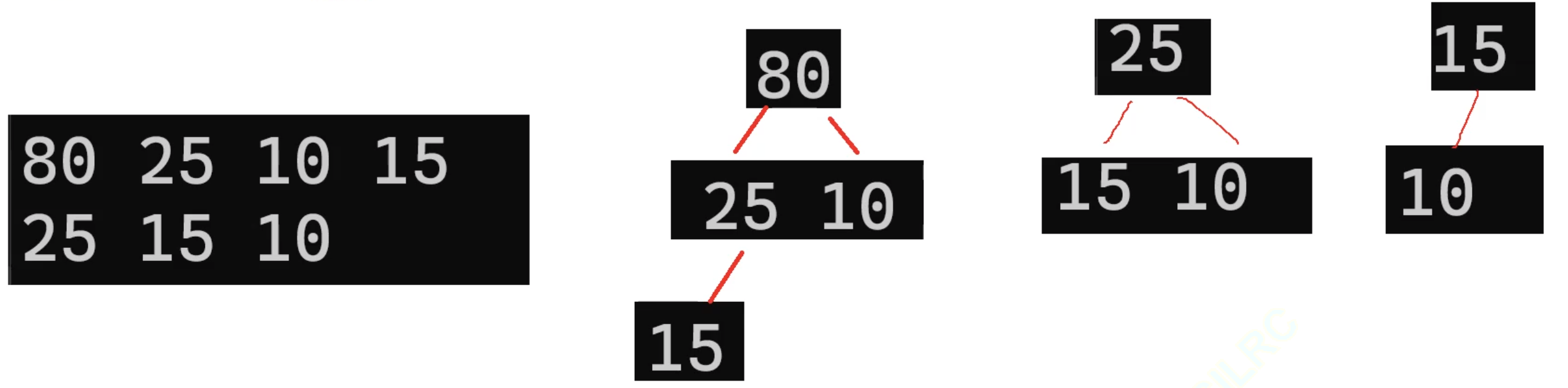
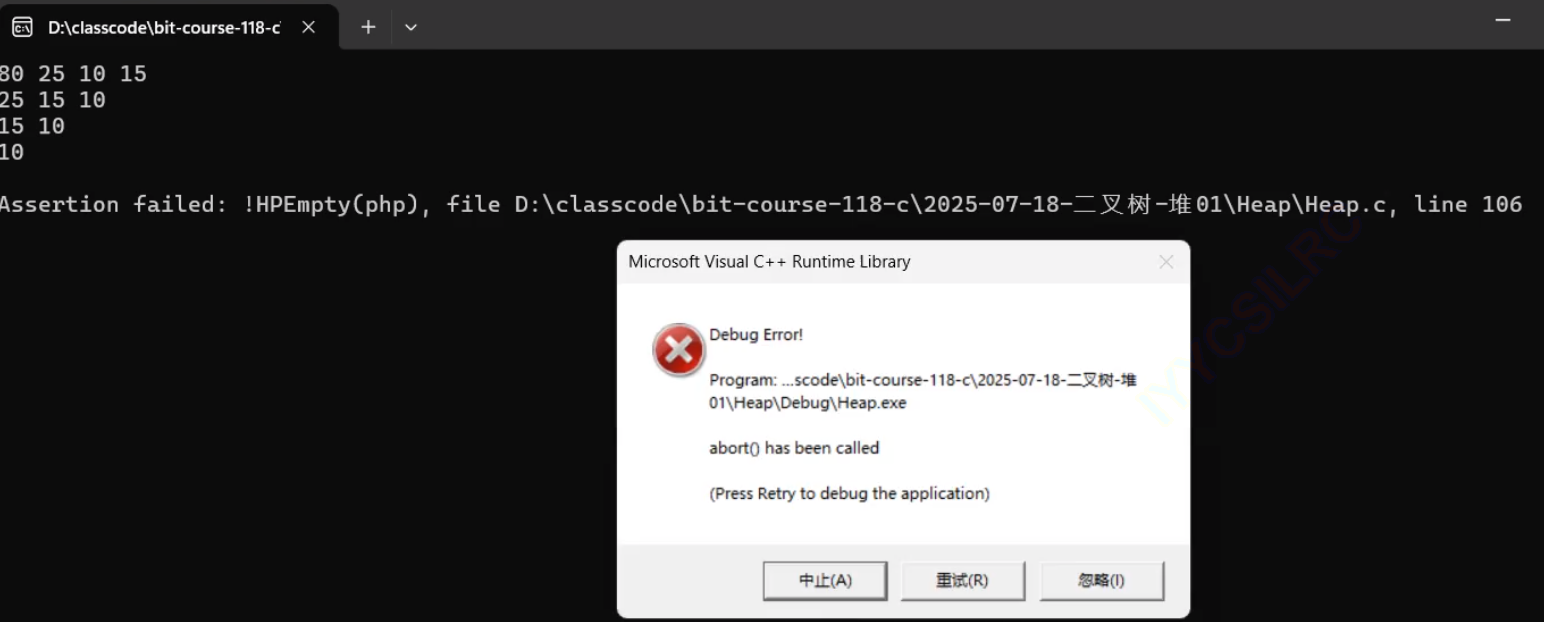
我们期望断言报错，事实上确实如此，那么出堆的代码就写好了。

（11）取堆顶元素

Heap.c：

HPDataType HPTop(HP* php)
{
	assert(!HPEmpty(php));
	return php->arr[0];
}

test.c：

#include"Heap.h"

void test01()
{
	HP hp;
	HPInit(&hp);
	HPPush(&hp, 25);
	HPPush(&hp, 15);
	HPPush(&hp, 10);
	HPPush(&hp, 56);
	HPPush(&hp, 70);
	HPPush(&hp, 30);
	HPPrint(&hp);

	while (!HPEmpty(&hp))
	{
		int top = HPTop(&hp);
		printf("%d ", top);
		HPPop(&hp);
	}

	HPDesTroy(&hp);
}
int main()
{
	test01();
	return 0;
}

（12）循环判断堆为不为空

test.c：

	while (!HPEmpty(&hp))
	{
		int top = HPTop(&hp);
		printf("%d ", top);
		HPPop(&hp);
	}

不断循环地判断堆顶为不为空，不为空，出堆顶——

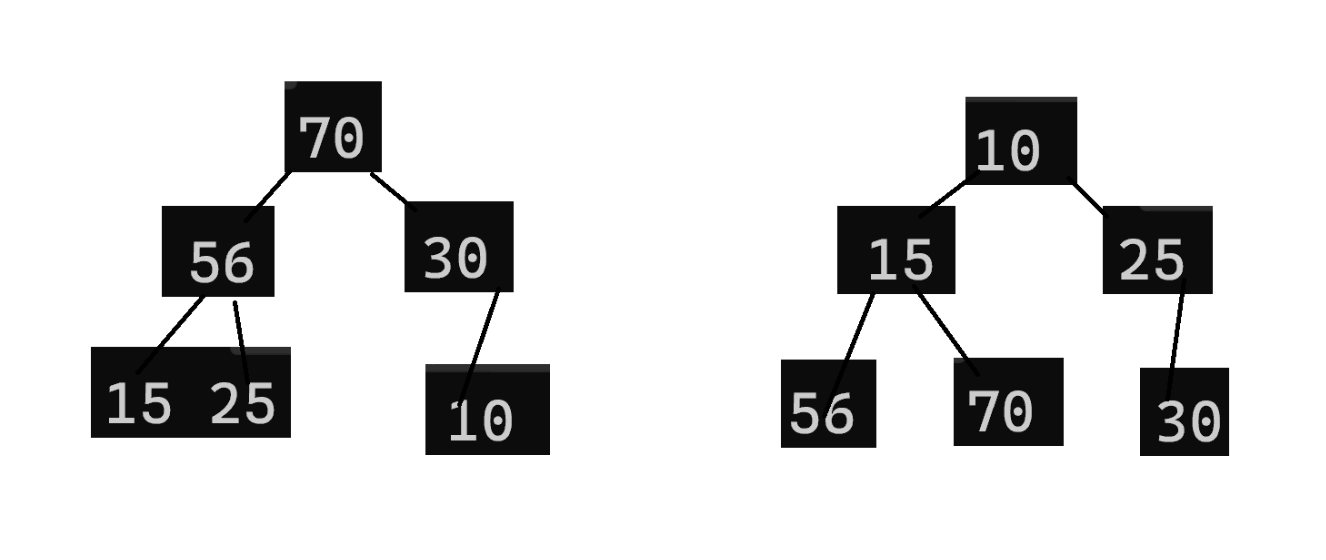
2、完整代码

（1）Heap.h：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

//定义堆结构
typedef int HPDataType;
typedef struct Heap {
	HPDataType* arr;
	int size;    //有效数据个数
	int capaicty;//空间大小
}HP;

void HPInit(HP* php);
void HPDesTroy(HP* php);

void HPPrint(HP* php);
void Swap(int* x, int* y);
//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n);
//向上调整算法
void AdjustUp(HPDataType* arr, int child);

void HPPush(HP* php, HPDataType x);
void HPPop(HP* php);
HPDataType HPTop(HP* php);

bool HPEmpty(HP* php);

（2）Heap.c：

#define  _CRT_SECURE_NO_WARNINGS  1

#include"Heap.h"

void HPInit(HP* php)
{
	assert(php);

	php->arr = NULL;
	php->size = php->capaicty = 0;
}
void HPDesTroy(HP* php)
{
	assert(php);
	if (php->arr)
		free(php->arr);
	php->arr = NULL;
	php->size = php->capaicty = 0;
}
void HPPrint(HP* php)
{
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->arr[i]);
	}
	printf("\n");
}
void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

//向上调整算法
void AdjustUp(HPDataType* arr, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//建大堆：>
		//建小堆: <
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else {
			break;
		}
	}
}
//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//建大堆：<
		//建小堆: >
		if (child + 1 < n && arr[child] > arr[child + 1])
		{
			child++;
		}
		//孩子和父亲比较
		//建大堆：>
		//建小堆:<
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else {
			break;
		}
	}
}

void HPPush(HP* php, HPDataType x)
{
	assert(php);
	//空间不够要增容
	if (php->size == php->capaicty)
	{
		//增容
		int newCapacity = php->capaicty == 0 ? 4 : 2 * php->capaicty;
		HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapacity * sizeof(HPDataType));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);
		}
		php->arr = tmp;
		php->capaicty = newCapacity;
	}
	//空间足够
	php->arr[php->size] = x;
	//向上调整
	AdjustUp(php->arr, php->size);
	++php->size;
}

bool HPEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

void HPPop(HP* php)
{
	assert(!HPEmpty(php));
	Swap(&php->arr[0], &php->arr[php->size - 1]);
	--php->size;
	//堆顶数据需要向下调整
	AdjustDown(php->arr, 0, php->size);
}

HPDataType HPTop(HP* php)
{
	assert(!HPEmpty(php));
	return php->arr[0];
}

（3）test.c：

#define  _CRT_SECURE_NO_WARNINGS  1

#include"Heap.h"

void test01()
{
	HP hp;
	HPInit(&hp);
	HPPush(&hp, 25);
	HPPush(&hp, 15);
	HPPush(&hp, 10);
	HPPush(&hp, 56);
	HPPush(&hp, 70);
	HPPush(&hp, 30);
	HPPrint(&hp);

	while (!HPEmpty(&hp))
	{
		int top = HPTop(&hp);
		printf("%d ", top);
		HPPop(&hp);
	}

	//HPPop(&hp);
	//HPPrint(&hp);
	//HPPop(&hp);
	//HPPrint(&hp);
	//HPPop(&hp);
	//HPPrint(&hp);
	//HPPop(&hp);
	//HPPrint(&hp);
	//HPPop(&hp);
	//HPPrint(&hp);

	HPDesTroy(&hp);

}

int main()
{
	test01();
	return 0;
}

（三）堆的应用——“堆排序”、堆排序和冒泡排序的比较与实现

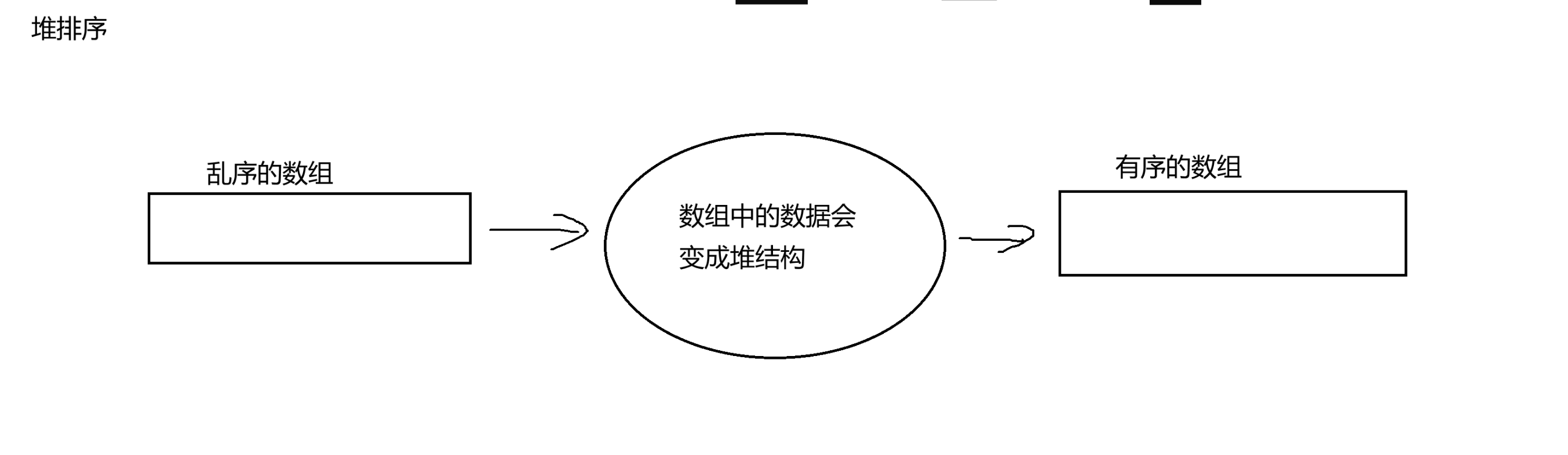
1、冒泡排序

冒泡排序是我们在C语言阶段就介绍过的排序方法——

test.c：

//冒泡排序
void BubbleSort(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n - i - 1; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				Swap(&arr[j], &arr[j + 1]);
			}
		}
	}
}

int main()
{
	//test01();
	int arr[6] = { 30,56,25,15,70,10 };

	printf("排序之前：\n");
	for (int i = 0; i < 6; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");

	//HeapSort(arr, 6);
	BubbleSort(arr, 6);

	printf("排序之后：\n");
	for (int i = 0; i < 6; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
	return 0;
}

2、“堆排序”

“堆排序“”——这不是实际的堆排序，调用了堆的结构。

test.c：

//堆排序----这不是实际的堆排序
void HeapSort01(int* arr, int n)
{
	HP hp;//-----使用数据结构-堆
	HPInit(&hp);
	//调用push将数组中的数据放入到堆中
	for (int i = 0; i < n; i++)
	{
		HPPush(&hp, arr[i]);
	}
	int i = 0;
	while (!HPEmpty(&hp))
	{
		int top = HPTop(&hp);
		arr[i++] = top;
		HPPop(&hp);
	}
	HPDesTroy(&hp);
}

3、堆排序

这个才是堆排序————使用的是堆结构的思想，而不是调用堆的结构。

排升序——建大堆；排降序——建小堆。

（1）降序

test.c：

//堆排序————使用的是堆结构的思想
void HeapSort(int* arr, int n)
{
	//乱序数组————建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(arr, i, n);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&arr[0], &arr[end]);
		AdjustDown(arr, 0, end);
		end--;
	}
}

int main()
{
	//test01();
	int arr[6] = { 30,56,25,15,70,10 };

	printf("排序之前：\n");
	for (int i = 0; i < 6; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");

	HeapSort(arr, 6);
	//BubbleSort(arr, 6);

	printf("排序之后：\n");
	for (int i = 0; i < 6; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
	return 0;
}

这里我们打印出来结果是降序的——

（2）升序

也可以是升序的——

test.c：

//堆排序————使用的是堆结构的思想
void HeapSort(int* arr, int n)
{
	//乱序数组————建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(arr, i, n);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&arr[0], &arr[end]);
		AdjustDown(arr, 0, end);
		end--;
	}
}
int main()
{
	//test01();
	int arr[6] = { 30,56,25,15,70,10 };

	printf("排序之前：\n");
	for (int i = 0; i < 6; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");

	HeapSort(arr, 6);
	//BubbleSort(arr, 6);

	printf("排序之后：\n");
	for (int i = 5; i >= 0; i--)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
	return 0;
}

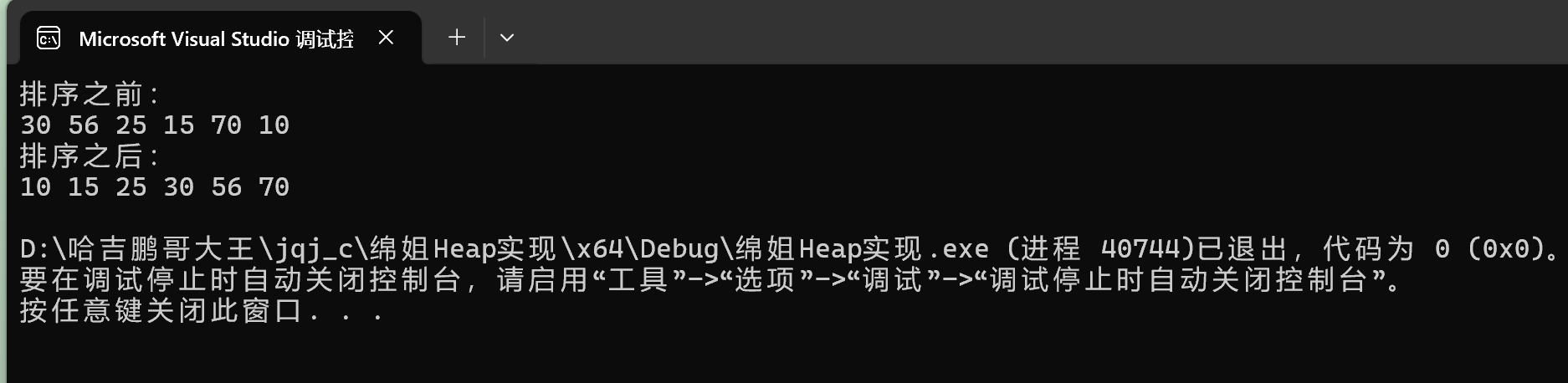
现在就是升序的了。

结尾

函数栈帧的创建与销毁相关博客的链接，博主已经放在正文前面了，有需要的友友自取。

往期回顾：

【数据结构与算法】数据结构初阶：详解二叉树（一）

【数据结构与算法】数据结构初阶：详解栈和队列（下）——队列

【数据结构与算法】数据结构初阶：详解栈和队列（上）——栈

【数据结构与算法】数据结构初阶：详解顺序表和链表（五）——双向链表

【数据结构与算法】数据结构初阶：详解顺序表和链表（四）——单链表（下）

【数据结构与算法】数据结构初阶：详解顺序表和链表（三）——单链表（上）

本期内容需要回顾的C语言知识如下面的截图中所示（指针博主写了6篇，列出来有水字数嫌疑了，就只放指针第六篇的网址，博主在指针（六）把指针部分的前五篇的网址都放在【往期回顾】了，点击【传送门】就可以看了）。大家如果对前面部分的知识点印象不深，可以去上一篇文章的结尾部分看看，博主把需要回顾的知识点相关的博客的链接都放在上一篇文章了，上一篇文章的链接博主放在下面了：

【数据结构与算法】数据结构初阶：详解顺序表和链表（三）——单链表（上）

结语：本篇文章到这里就结束了，对数据结构的二叉树知识感兴趣的友友们可以在评论区留言，博主创作时可能存在笔误，或者知识点不严谨的地方，大家多担待，如果大家在阅读的时候发现了行文有什么错误欢迎在评论区斧正，再次感谢友友们的关注和支持！

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-11-12，如有侵权请联系 cloudcommunity@tencent.com 删除

数据结构与算法

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度