【优选算法必刷100题】第029~30题（前缀和算法）：寻找数组的中心下标、除自身以外数组的乘积

艾莉丝努力练剑

发布于 2025-11-16 20:24:04

290

文章被收录于专栏：C / C++C / C++

029 和为 K 的子数组

力扣链接：560. 和为 K 的子数组

力扣题解链接：前缀和 + 哈希表解决【和为 K 的子数组】问题

题目描述：

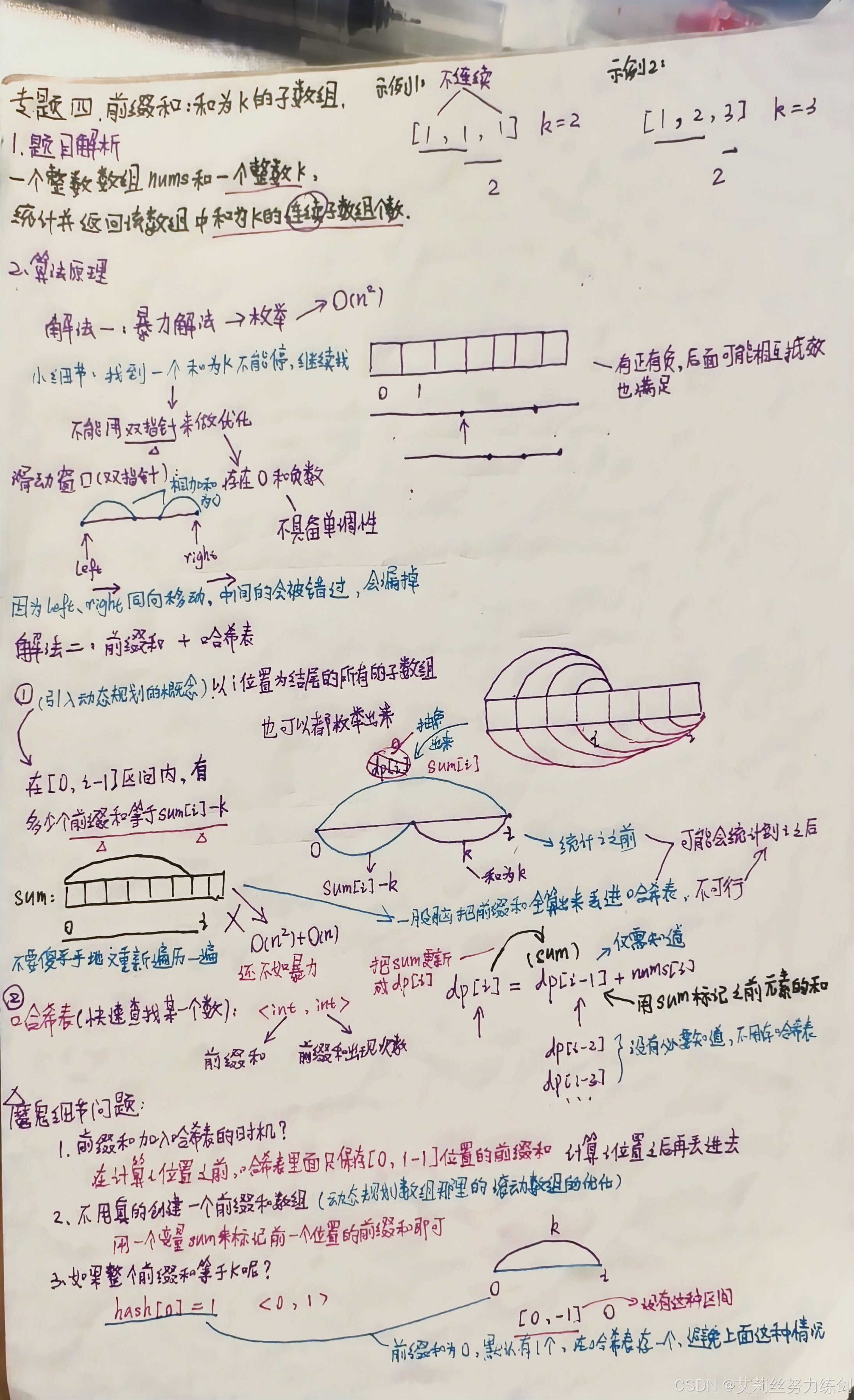
1.1 算法思路：前缀和+哈希表~>将前缀和存在哈希表中

参考下图：

设为数组中的任意位置，用sum[ i ]表示[0 , i]区间内所有元素的和。

如果想知道有多少个【以为结尾的和为的子数组】，就要找到有多少个起始位置为x1，x2，x3...使得[x , i]区间内的所有元素的和为k。那么[0 , x]区间内的和是不是就是sum[ i ] - k了。于是问题就变成——

找到在[0 , i - 1]区间内，有多少前缀和等于sum[ i ] - k的即可。我们不需要真的去初始化一个前缀和数组，因为我们只关心在 i 位置之前，有多少个前缀和会等于sum[ i ] - k。因此，我们仅需用一个哈希表，一边求当前位置的前缀和，一边存下之前每一种前缀和出现的次数。

1.2 算法实现

1.2.1 C++实现

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map <int,int> hash; // 统计前缀和出现的次数
        // 细节
        hash[0] = 1;
        // 用一个变量标记一下前缀和
        int sum = 0,ret = 0;
        for(auto x : nums)
        {
            sum += x; // 计算当前位置的前缀和
            if(hash.count(sum - k)) ret += hash[sum - k];
            hash[sum]++;
        }
        return ret;
    }
};

时间复杂度：O(n)，空间复杂度：O(1)。

1.2.2 Java实现

// Java写法
class Solution {
	public int subarraySum(int[] nums, int k) {
		Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
		hash.put(0, 1);
		int sum = 0, ret = 0;
		for (int x : nums)
		{
			sum += x; // 计算当前位置的前缀和 
			ret += hash.getOrDefault(sum - k, 0); // 统计结果 
			hash.put(sum, hash.getOrDefault(sum, 0) + 1); // 把当前的前缀和丢到哈希表里面
		}
		return ret;
	}
}

时间复杂度：O(n)，空间复杂度：O(1)。

1.3 博主手记

本题整个的思路、算法原理、解题过程博主在纸上推导了一遍，大家可以参考一下手记的推导过程！最好做题的过程中自己也推导一遍！！！自己能够推导很重要！

030 和可被K整除的子数组

本题是某一年的蓝桥杯竞赛原题哦！桀桀桀，大家做做看吧！

力扣链接：974. 和可被 K 整除的子数组

力扣题解链接：前缀和 + 哈希表解决【和可被K整除的子数组】问题

题目描述：

2.1 解法一：暴力枚举

暴力解法就是枚举出所有的子数组的和，这里不再赘述。

2.2 解法二：前缀和（余数）存在哈希表中

2.2.1 补充知识

2.2.1.1 （数学公式）同余定理

如果(a - b）% n == 0，那么我们可以得到一个结论：a % n == b % n。用文字叙述就是，如果两个数相减的差能被n整除，那么这两个数对n取模的结果相同。

例如：(26 - 2) %12 == 0，那么26 %12 == 2 % 12 == 2。

2.2.1.2 c++中负数取模的结果，以及如何修正【负数取模】的结果

（1）c++中关于负数的取模运算，结果是【把负数当成正数，取模之后的结果加上一个负号】。

例如：-1 % 3 = (-1 % 3) = -1

（2）因为有负数，为了防止发生【出现负数】的结果，以（a%n+n）%n的形式输出保证为正。

例如：-1 % 3 =（-1 % 3 + 3） % 3 = 2

2.2.2 算法思路

思路与560.和为K的子数组这道题的思路相似。

还是用这张图——

设为数组中的任意位置，用sum[ i ]表示[0，i]区间内所有元素的和。

1、想知道有多少个「以i为结尾的可被k整除的子数组」，就要找到有多少个起始位置为x1，x2，x3...使得[x，i]区间内的所有元素的和可被k整除。

2、设[0，x - 1]区间内所有元素之和等于a，[0，i]区间内所有元素的和等于，可得(b - a) % k == 0。

3、由同余定理可得，[0，x - 1]区间与[0，i]区间内的前缀和同余。于是问题就变成——

（1）找到在[0，i－1]区间内，有多少前缀和的余数等于sum[ i ] % k的即可。

我们不用真的初始化一个前缀和数组，因为我们只关心在 i 位置之前，有多少个前缀和等于sum[ i ] - k。因此，我们仅需用一个哈希表，一边求当前位置的前缀和，一边存下之前每一种前缀和出现的次数。

2.3 算法实现

2.3.1 C++实现

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) {
        unordered_map<int,int> hash; // 统计前缀和出现的次数
        // 处理细节
       hash[0] = 1; // 这里存的依旧是余数，只不过0 % k还是0，所以这里存的是0这个数的余数
        int sum = 0,ret = 0;
        for(auto x : nums)
        {
            sum += x; // 算出当前位置的前缀和
            // 求出修正后的余数
            int r = (sum % k + k) % k;
            if(hash.count(r))
                ret += hash[r]; // 统计结果
                hash[r]++; // 继续遍历
        }
        return ret;
    }
};

时间复杂度：O(n)，空间复杂度：O(1)。

2.3.2 Java实现

// Java写法
class Solution {
	public int subarraysDivByK(int[] nums, int k) {
		Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
		hash.put(0 % k, 1);
		int sum = 0, ret = 0;
		for (int x : nums)
		{
			sum += x; // 计算当前位置的前缀和 
			int r = (sum % k + k) % k;
			ret += hash.getOrDefault(r, 0); // 统计结果 
			hash.put(r, hash.getOrDefault(r, 0) + 1);
		}
		return ret;
	}
};