[Java数据结构与算法]深入理解优先级队列与堆

木井巳

发布于 2025-12-16 09:35:01

1470

一、引言

在计算机科学中，队列是一种常见的数据结构，遵循先进先出（FIFO）的原则。

然而，在实际应用中，我们经常会遇到需要根据优先级处理元素的场景。

比如操作系统中进程调度、游戏中的事件处理、数据流中的高频元素统计等，这些场景都需要优先级高的元素能够优先被处理。

优先级队列（Priority Queue）就是为解决这类问题而设计的数据结构。它不同于普通队列的FIFO特性，而是根据元素的优先级进行出队操作，优先级最高的元素总是最先出队。

本文将深入探讨优先级队列的底层实现——堆（Heap），从基本概念到具体实现，从理论分析到实际应用，帮助读者全面掌握这一重要数据结构。

二、什么是优先级队列？

2.1 基本概念

优先级队列是一种抽象数据类型，它支持以下两个基本操作：

插入（Insert）：添加一个带有优先级的元素
提取最高优先级（Extract-Max/Min）：移除并返回优先级最高或最低的元素

与普通队列相比，优先级队列的出队顺序不是由元素的入队时间决定，而是由元素的优先级决定。

三、堆：优先级队列的底层实现

3.1 堆的基本概念

3.1.1 堆的定义

堆是一种特殊的完全二叉树，它满足以下性质：

对于大根堆：每个节点的值都大于或等于其子节点的值
对于小根堆：每个节点的值都小于或等于其子节点的值

比如一组数据：27，15，19，18，28，34，65，49，25，37

根据这组数据建立的小根堆和大根堆如下图：

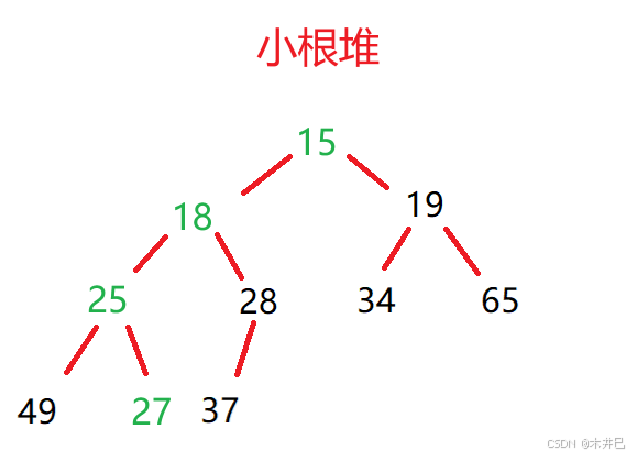
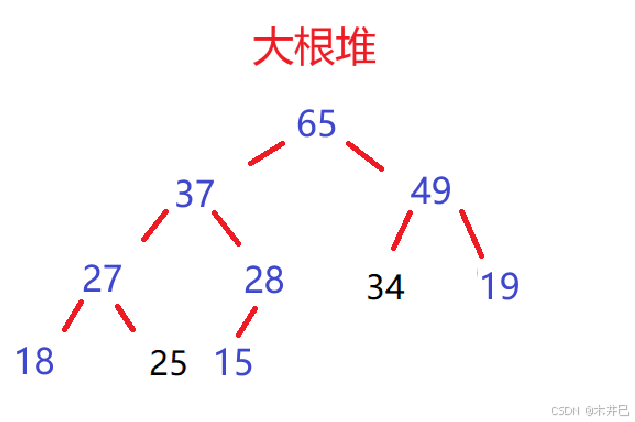
3.1.2 堆的存储

由于堆是完全二叉树，我们可以使用数组来高效存储，不需要使用指针。

这种存储方式既节省空间，又能快速定位任意节点的父节点和子节点。

public class Heap {
    public int[] elem;    // 用数组存储数据
    public int usedSize;  // 记录堆的大小

    public Heap() {
        this.elem = new int[10];
    }
}

3.2 堆的核心操作

3.2.1 向下调整（Shift Down）

向下调整是堆的核心操作之一，用于维护堆的性质。

当某个节点的值发生变化（通常是变小在大根堆中或变大在小根堆中），可能需要向下调整。

向下调整建大根堆的思路：

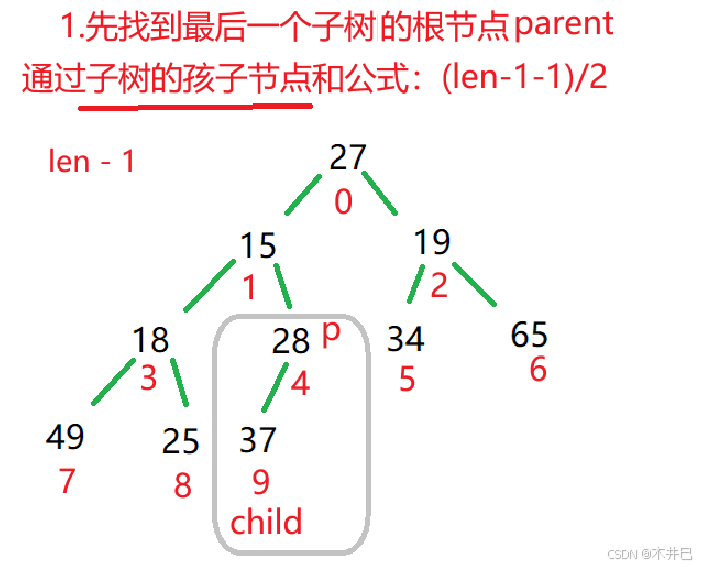
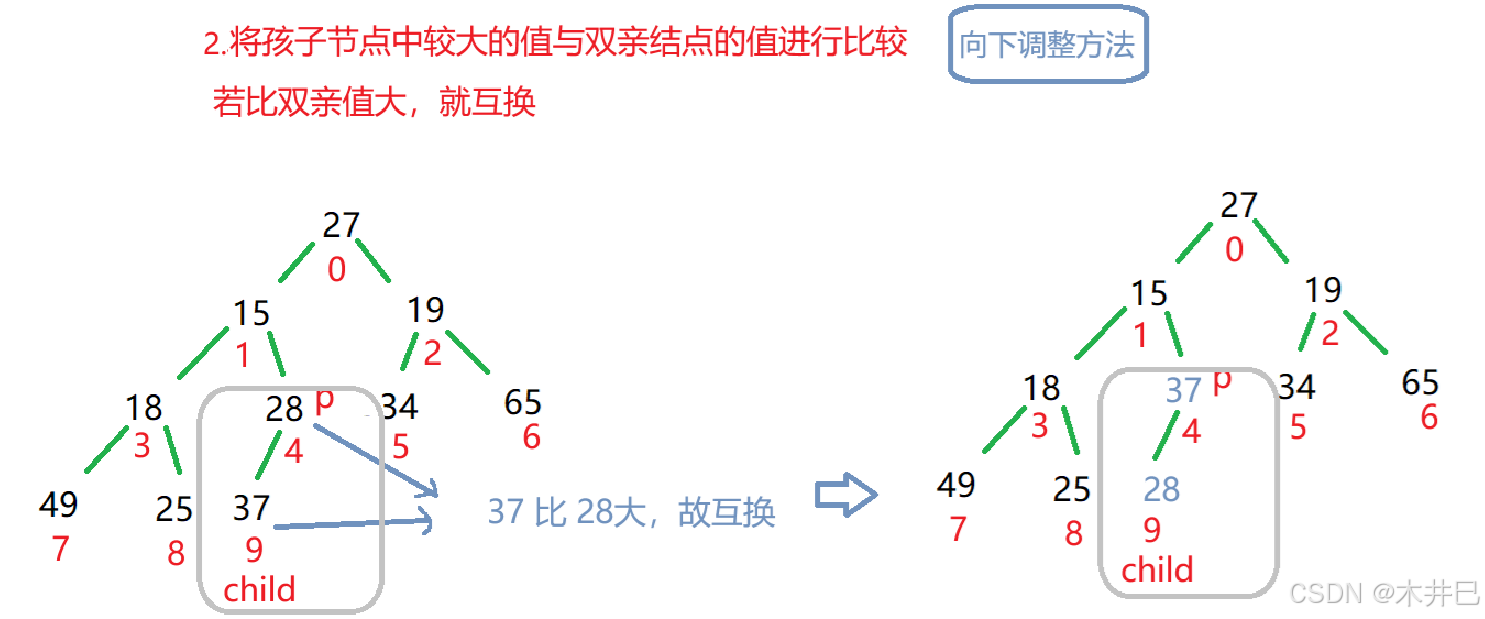
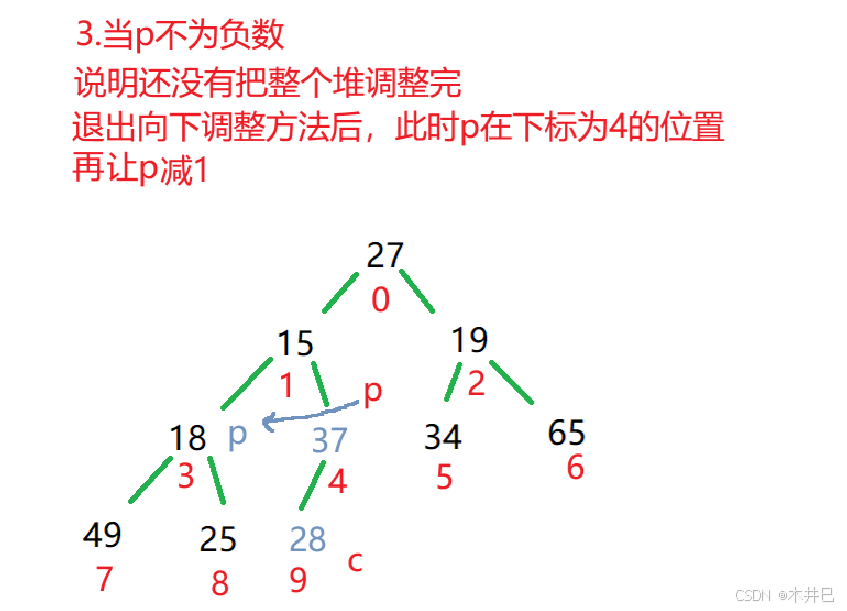
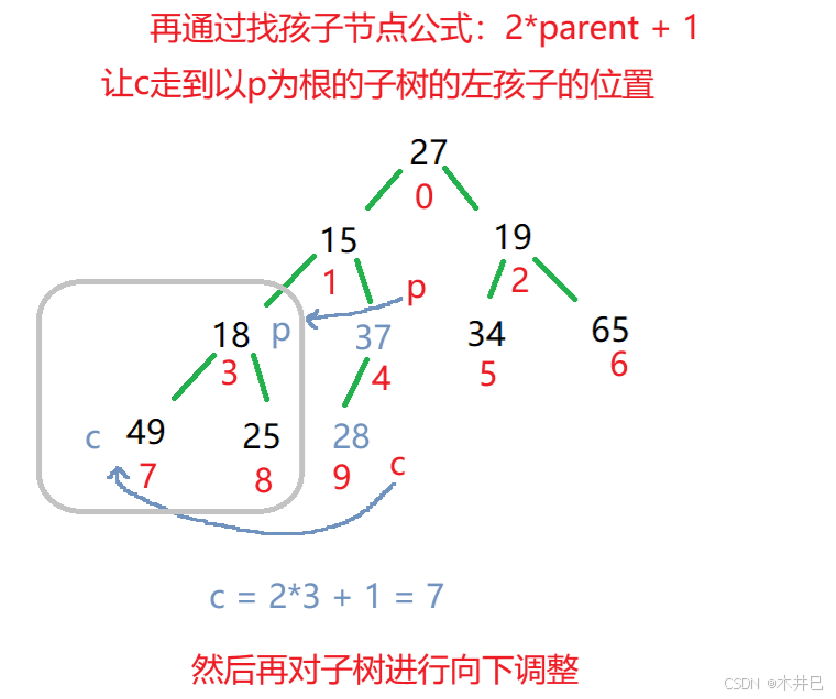
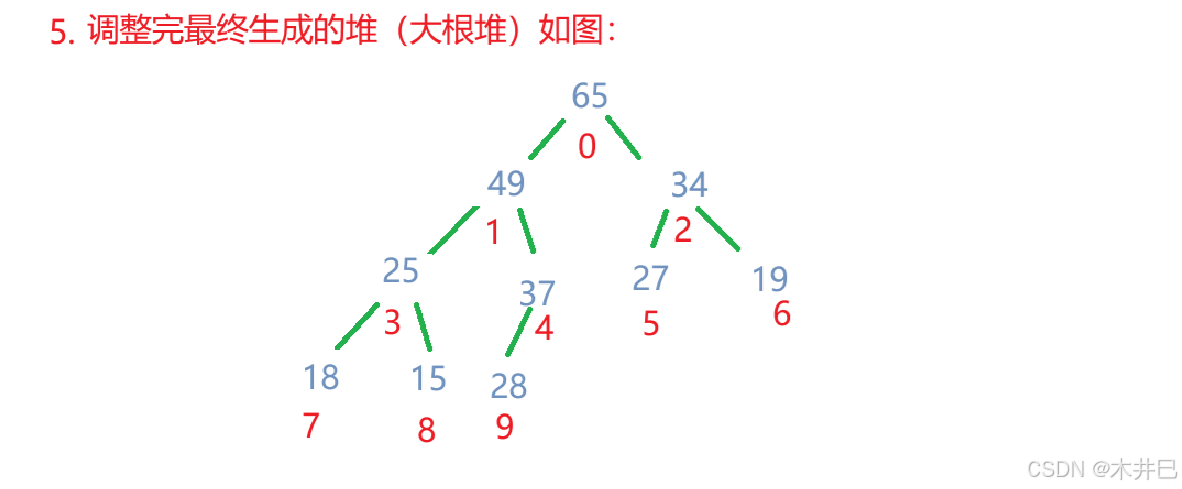
算法实现如下：

// 向下调整建立大根堆
public void createHeap() {
    for (int parent = (this.usedSize-1-1)/2; parent >= 0; parent--) {
        shiftDown(parent,this.usedSize);
    }
}

// 向下调整方法
private void shiftDown(int parent, int usedSize) {  //param: 起始位置和结束位置
    int child = 2*parent + 1;
    // 当还没有将所有的子树改成大根堆时
    while (child < this.usedSize) {
        // 找到孩子节点中的最大值
        if ((child+1)<this.usedSize && elem[child]<elem[child+1]) {
            child++;
        }
        // 将找到的最大值与双亲的值进行比较
        if (elem[child] > elem[parent]) {
            // 若比双亲的值大，进行交换
            swap(elem,child,parent);
            // 然后往子树走
            parent = child;
            child = 2*parent + 1;
        } else {
            // 若比双亲的值小，就直接退出
            break;
        }
    }
}

向下调整方法的时间复杂度：最坏情况下，需要从根节点调整到叶子节点，调整路径的长度为树的高度，因此时间复杂度为 O ( logN )。

而向下调整建堆的时间复杂度是 O ( NlogN )，通常N是很小的数字，故可近似为 O ( N )。

3.2.2 向上调整（Shift Up）

向上调整用于在堆中插入新元素时维护堆的性质。新元素通常放在堆的末尾，然后通过向上调整找到其合适位置。

向上调整方法的思路：

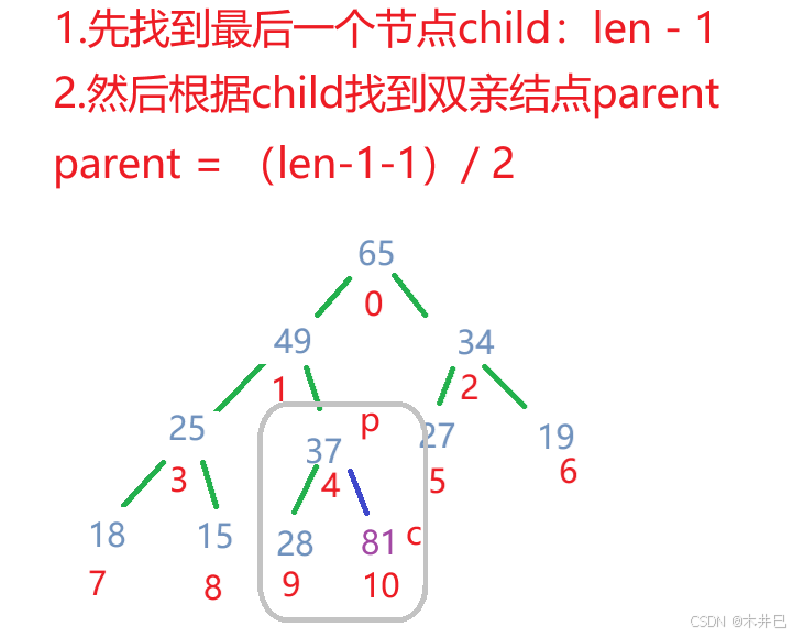
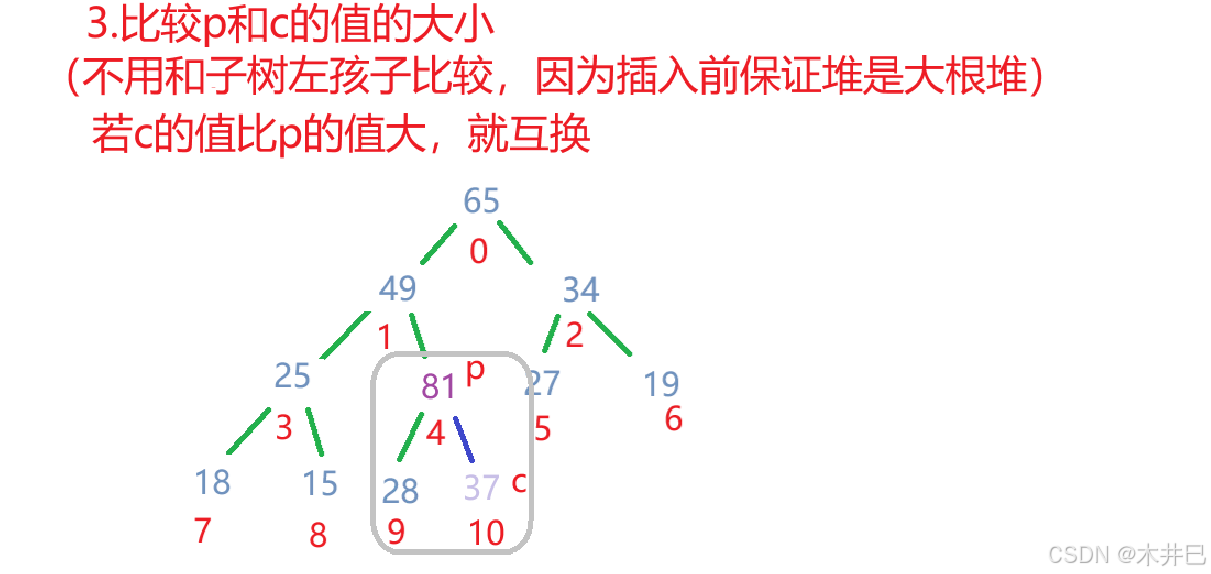
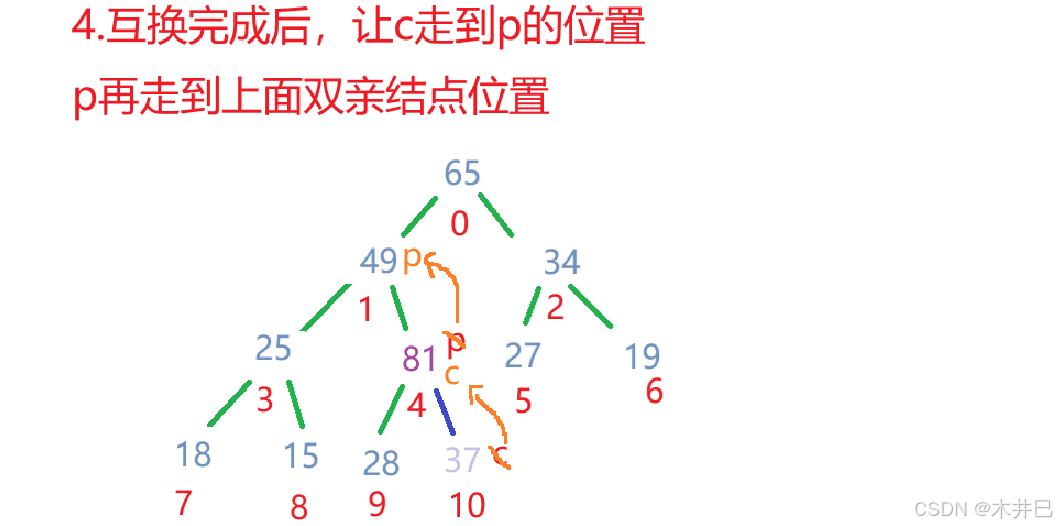
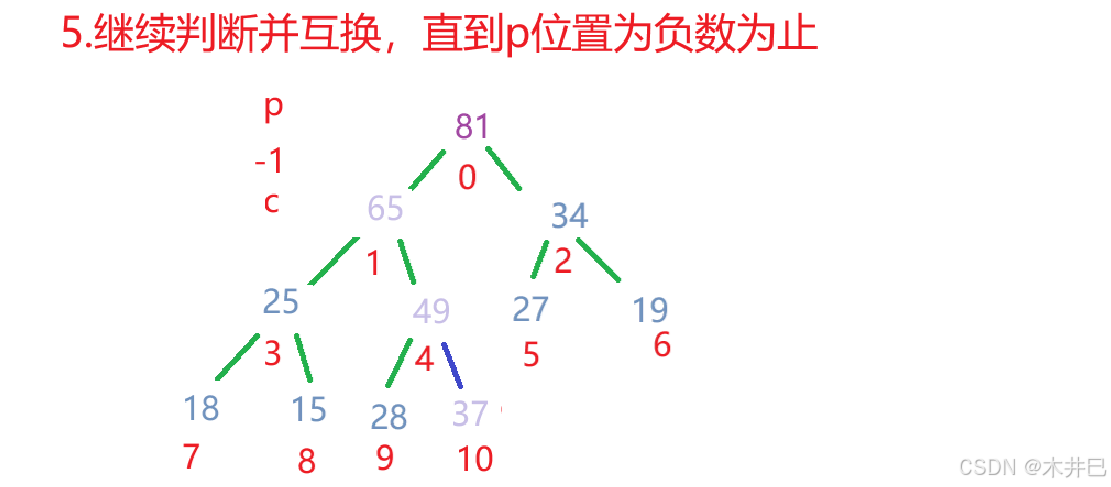
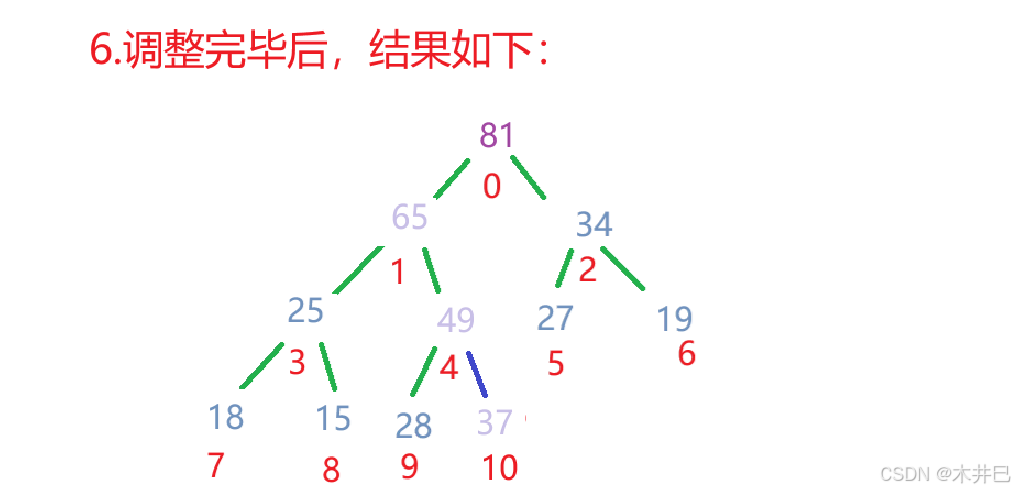
算法实现如下：

// 向上调整方法
private void shiftUp(int child) {
    int parent = (child-1) / 2;
    while (parent >= 0) {
        // 将新元素与双亲的值比较
        if (elem[child] > elem[parent]) {
            // 若比双亲的值大，进行交换
            swap(elem,child,parent);
            // 然后往父树走
            child = parent;
            parent = (child-1) / 2;
        } else {
            // 若比双亲的值小，就直接退出
            break;
        }
    }
}

3.2.3 插入与删除操作

堆的插入：

将新元素放入堆的末尾
对新元素执行向上调整

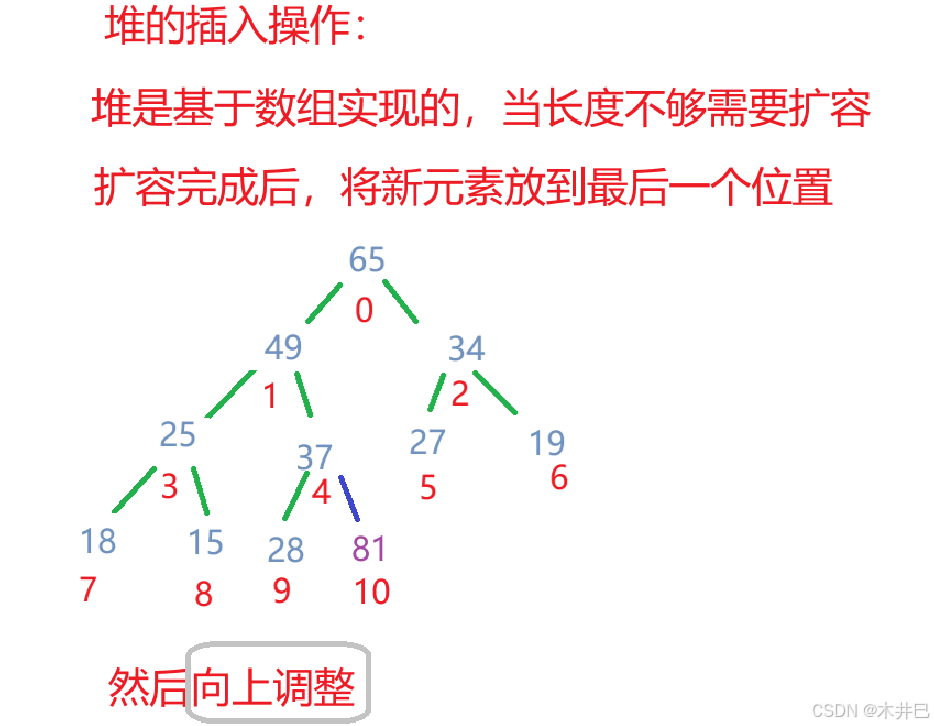
算法实现如下：

// 插入操作
public void offer(int val) {
    // 判断是否已满，若满就扩容
    if (isFull()) {
        this.elem = Arrays.copyOf(this.elem,2*this.elem.length);
    }
    // 把新元素放入最后一个节点
    elem[usedSize] = val;
    // 向上扩容调整大根堆
    shiftUp(usedSize++);
}

private boolean isFull() {
    return this.usedSize == this.elem.length;
}

// 向上调整方法
private void shiftUp(int child) {
    int parent = (child-1) / 2;
    while (parent >= 0) {
        // 将新元素与双亲的值比较
        if (elem[child] > elem[parent]) {
            // 若比双亲的值大，进行交换
            swap(elem,child,parent);
            // 然后往父树走
            child = parent;
            parent = (child-1) / 2;
        } else {
            // 若比双亲的值小，就直接退出
            break;
        }
    }
}

堆的删除：

将堆顶元素与最后一个元素交换
减少堆的大小
对新的堆顶元素执行向下调整

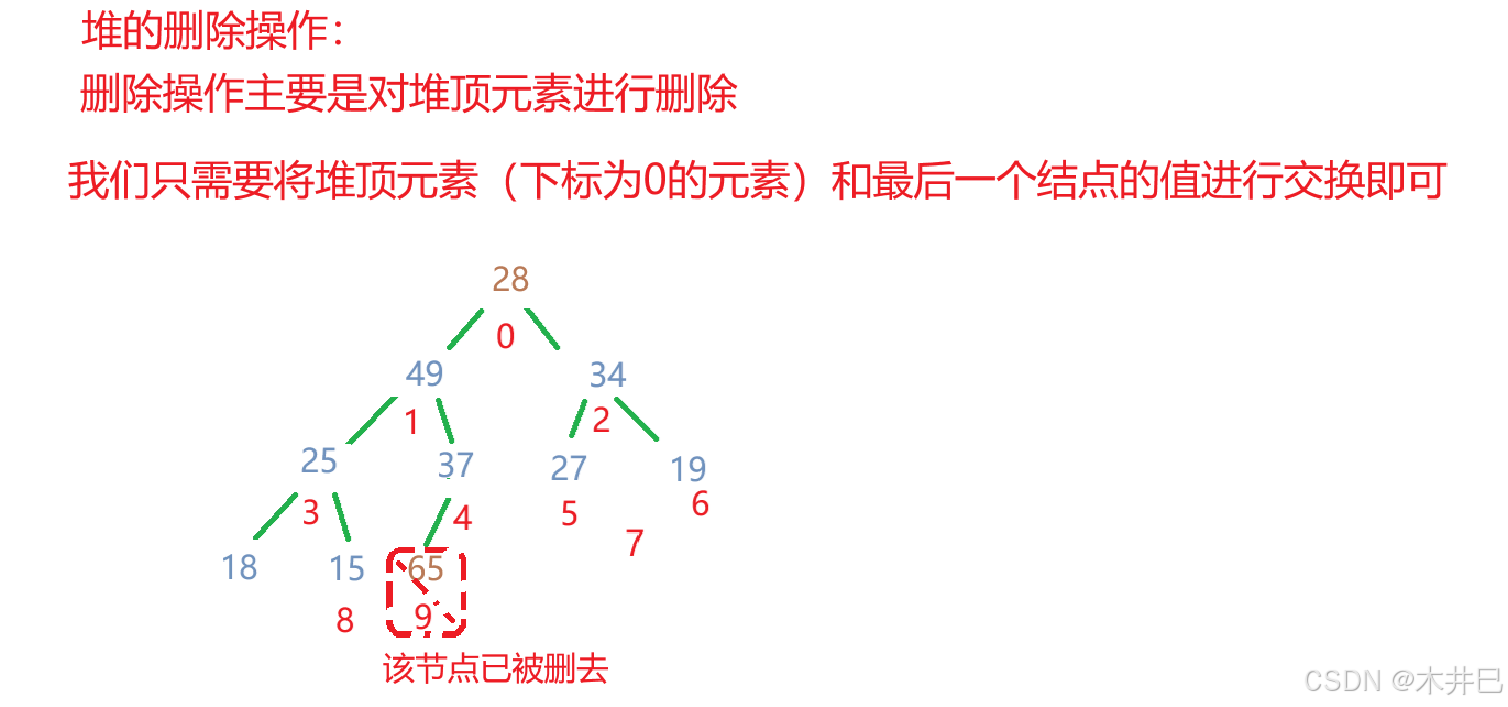
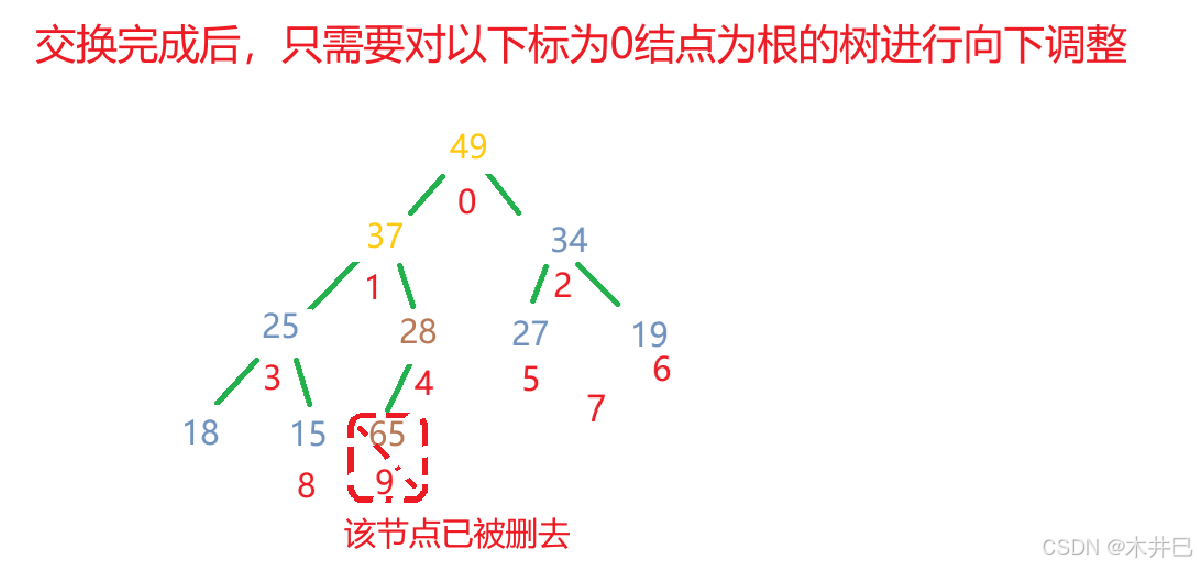
算法实现如下：

// 删除操作
public int poll() {
    // 如果堆为空，返回-1
    if (isEmpty())
        return -1;

    int end = this.usedSize - 1;
    int val = elem[0];

    // 把堆顶元素和最后元素交换
    swap(elem,0,end);

    // 向下调整以堆顶元素为根的树即可
    shiftDown(0,end);

    this.usedSize--;
    return val;
}

private boolean isEmpty() {
    return this.usedSize == 0;
}

public void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// 向下调整方法
private void shiftDown(int parent, int usedSize) {  //param: 起始位置和结束位置
    int child = 2*parent + 1;
    // 当还没有将所有的子树改成大根堆时
    while (child < this.usedSize) {
        // 找到孩子节点中的最大值
        if ((child+1)<this.usedSize && elem[child]<elem[child+1]) {
            child++;
        }
        // 将找到的最大值与双亲的值进行比较
        if (elem[child] > elem[parent]) {
            // 若比双亲的值大，进行交换
            swap(elem,child,parent);
            // 然后往子树走
            parent = child;
            child = 2*parent + 1;
        } else {
            // 若比双亲的值小，就直接退出
            break;
        }
    }
}

四、Java中的PriorityQueue

4.1 基本特性

Java提供了 PriorityQueue类作为优先级队列的实现：

线程不安全
不允许null元素
元素必须实现Comparable接口或提供Comparator
默认是小根堆

4.2 构造方法

// 1. 默认构造方法（小根堆，初始容量11）
PriorityQueue<Integer> pq1 = new PriorityQueue<>();

// 2. 指定初始容量
PriorityQueue<Integer> pq2 = new PriorityQueue<>(100);

// 3. 使用集合初始化
List<Integer> list = Arrays.asList(5, 3, 8, 1, 2);
PriorityQueue<Integer> pq3 = new PriorityQueue<>(list);

// 4. 使用自定义比较器（大根堆）
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);

4.3 自定义比较器

// 大根堆比较器
class DescComparator implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2.compareTo(o1); // 降序排列
    }
}

// 使用示例
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new DescComparator());

4.4 扩容机制

Java的PriorityQueue有自动扩容机制：

当容量小于64时，按当前容量的2倍扩容
当容量大于等于64时，按当前容量的1.5倍扩容
最大容量为Integer.MAX_VALUE - 8

五、堆的实战

5.1 堆排序

从小到大升序——>大根堆从大到小降序——>小根堆

算法实现思路（升序，使用大根堆）：

将堆顶元素即下标为0的元素和堆底最后一个元素end交换，交换完成后end--
向下调整，每一次调整end都要减一
堆从后往前就逐渐由大到小排序了
当end大于0时才进行以上操作，否则结束循环

算法实现如下：

// 堆排序
public void heapSort() {
    int end = this.usedSize - 1;    // end表示最后的元素

    // 遍历数据，当最后元素下标不为负数就一直排序
    while (end > 0) {
        // 堆顶元素和下标为end的元素进行交换
        swap(elem,0,end);

        // 向下调整
        shiftDown(0, end--);
    }
}

public void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// 向下调整方法
private void shiftDown(int parent, int usedSize) {  //param: 起始位置和结束位置
    int child = 2*parent + 1;
    // 当还没有将所有的子树改成大根堆时
    while (child < this.usedSize) {
        // 找到孩子节点中的最大值
        if ((child+1)<this.usedSize && elem[child]<elem[child+1]) {
            child++;
        }
        // 将找到的最大值与双亲的值进行比较
        if (elem[child] > elem[parent]) {
            // 若比双亲的值大，进行交换
            swap(elem,child,parent);
            // 然后往子树走
            parent = child;
            child = 2*parent + 1;
        } else {
            // 若比双亲的值小，就直接退出
            break;
        }
    }
}

5.2 Top-K

返回最小的K个数

思路一：整体排序；
思路二：建立一个大小为K的小根堆；
思路三：把前K个元素创建为大小为K的大根堆，遍历剩下的N-K个元素并依次与堆顶元素比较大小，若比堆顶元素小就调换

我们这里采用思路三：

假设数据是：12，5，7，9，3

要返回前3个最小的数

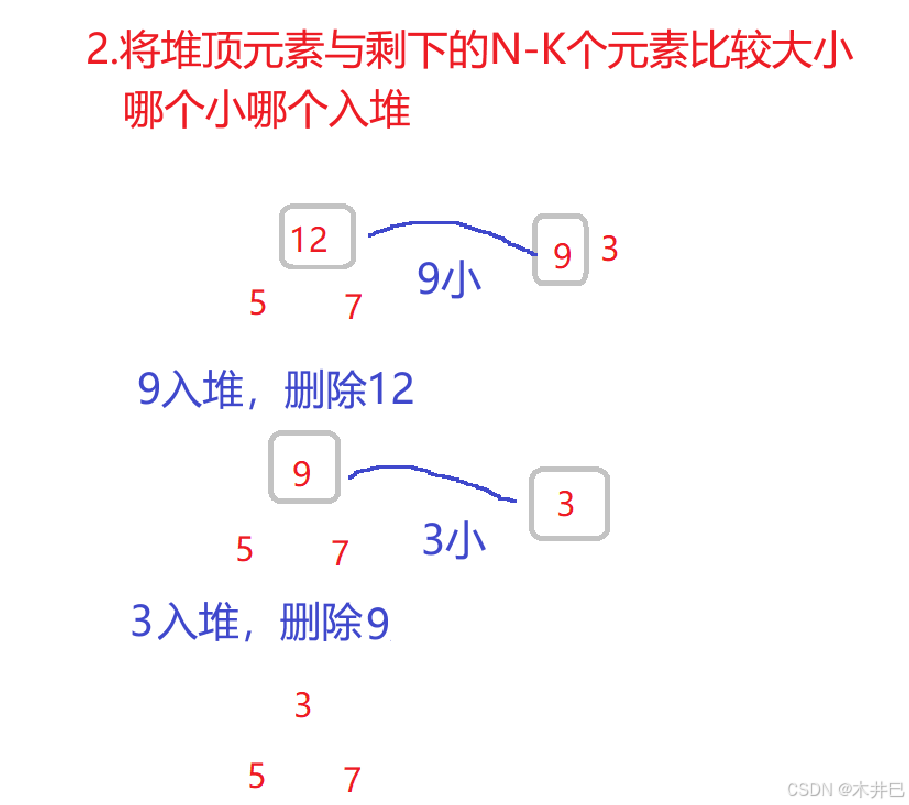
我们这里采用Java内置的PriorityQueue，它会自动进行调整
在进行实例化优先级队列的时候，我们采用自定义比较器，保证建立的是大根堆

算法实现如下：

// 自定义比较器
class Intcmp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2.compareTo(o1);
    }
}

public int[] smallestK(int[] arr, int k) {
    int[] ret = new int[k];
    if (arr==null || k==0)
        return ret;

    // 创建大小为K的大根堆
    PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(k,new Intcmp());
    for (int i = 0; i < k; i++) {
        priorityQueue.offer(arr[i]);
    }

    // 比较堆顶元素
    for (int i = k; i < arr.length; i++) {
        int val = priorityQueue.peek();
        if (arr[i] < val) {
            priorityQueue.poll();
            priorityQueue.offer(arr[i]);
        }
    }

    // 将大根堆存入数组
    for (int i = 0; i < k; i++) {
        ret[i] = priorityQueue.poll();
    }
    return ret;
}

希望读者看到这里，能够掌握以上的基本知识并熟练运用。

完

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-10-19，如有侵权请联系 cloudcommunity@tencent.com 删除

算法