C语言实战:高效计算2-100之间的质数(附两种经典算法)
C语言实战:高效计算2-100之间的质数(附两种经典算法)
用户11944663
发布于 2025-12-22 11:16:38
发布于 2025-12-22 11:16:38
C语言实战:高效计算2-100之间的质数(附两种经典算法)
质数(素数)是指大于1且除了1和自身外不能被其他数整除的自然数,在密码学、数论等领域有重要应用。今天我们通过C语言实现2-100之间质数的计算,对比两种经典算法的效率差异,帮你理解质数判断的核心逻辑与优化思路。
方法一:逐个判断法(基础高效版)
在这里插入图片描述
这种方法的思路很直接:遍历2-100的所有数字,对每个数字单独判断是否为质数,最后统计总数。
完整代码实现
#include <stdio.h>
#include <math.h>
// 素数判断函数(高效版)
int isPrime(int num) {
if (num <= 1) return 0; // 小于等于1的数不是质数
if (num == 2) return 1; // 2是质数(唯一的偶数质数)
if (num % 2 == 0) return 0; // 偶数一定不是质数
int sqrt_num = sqrt(num); // 计算平方根,减少循环次数
for (int i = 3; i <= sqrt_num; i += 2) { // 只判断奇数除数
if (num % i == 0) return 0; // 能被整除则不是质数
}
return 1; // 是质数
}
int main() {
int count = 0; // 统计质数的数量
printf("2-100 之间的质数有:\n");
// 遍历2到100的所有数
for (int num = 2; num <= 100; num++) {
if (isPrime(num)) {
printf("%d ", num); // 输出质数
count++; // 数量加1
}
}
printf("\n2-100 之间共有 %d 个质数\n", count);
return 0;
}代码优化点解析
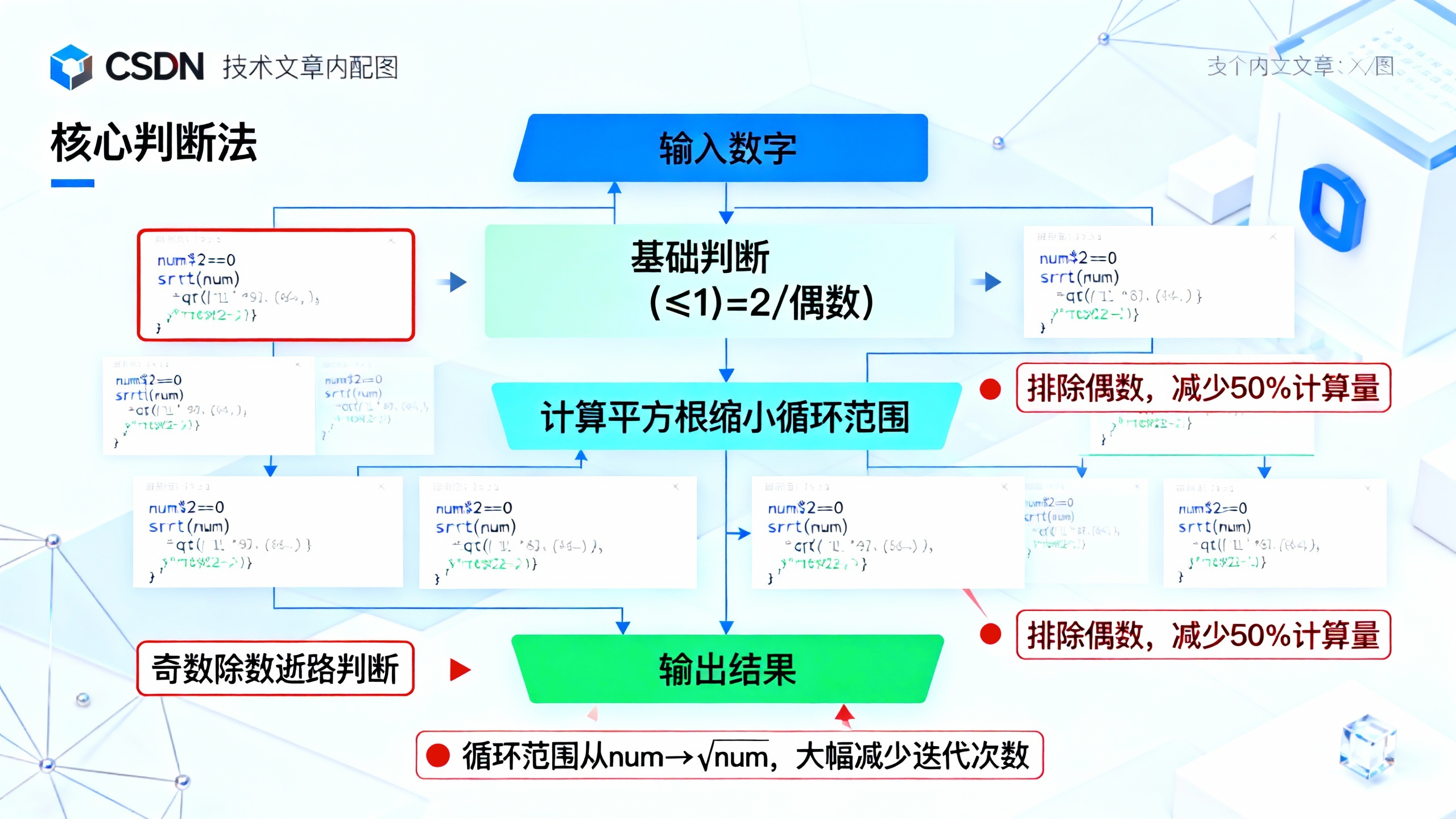
这个实现比最基础的判断方法效率提升明显,关键优化点在isPrime函数:
- 排除偶数:除了2之外,所有偶数都不是质数,因此直接判断
num%2==0即可排除大部分非质数,后续只需判断奇数除数。 - 减少循环范围:一个数如果不是质数,一定有一个小于等于其平方根的因数。例如判断37是否为质数,只需验证到6(√37≈6.08)即可,无需遍历到36,大幅减少循环次数。
- 除数步进优化:除数从3开始,每次+2(只判断奇数),再次减少一半的计算量。
运行结果
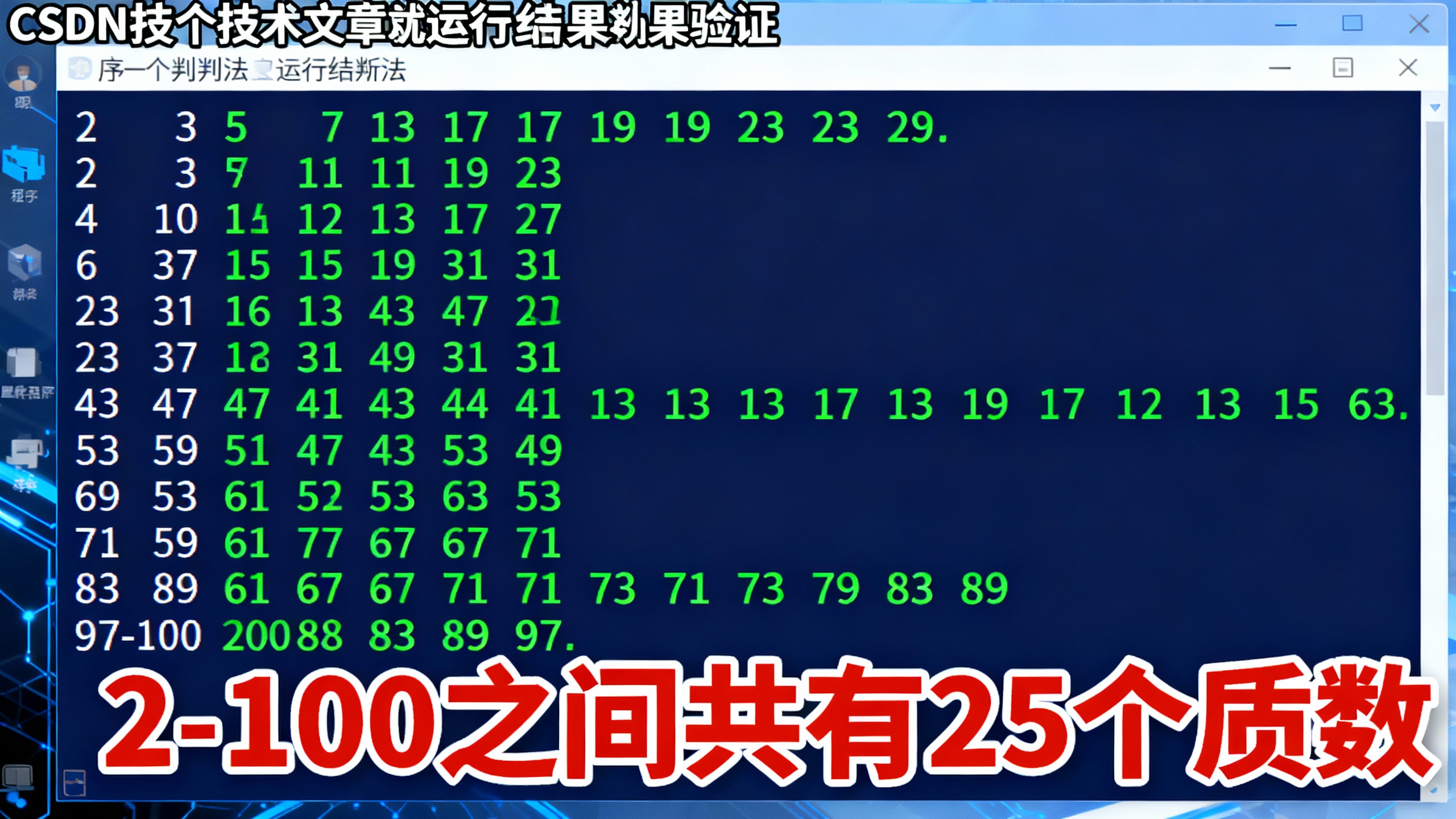
在这里插入图片描述
2-100 之间的质数有:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
2-100 之间共有 25 个质数方法二:埃拉托斯特尼筛法(高效批量计算)
在这里插入图片描述
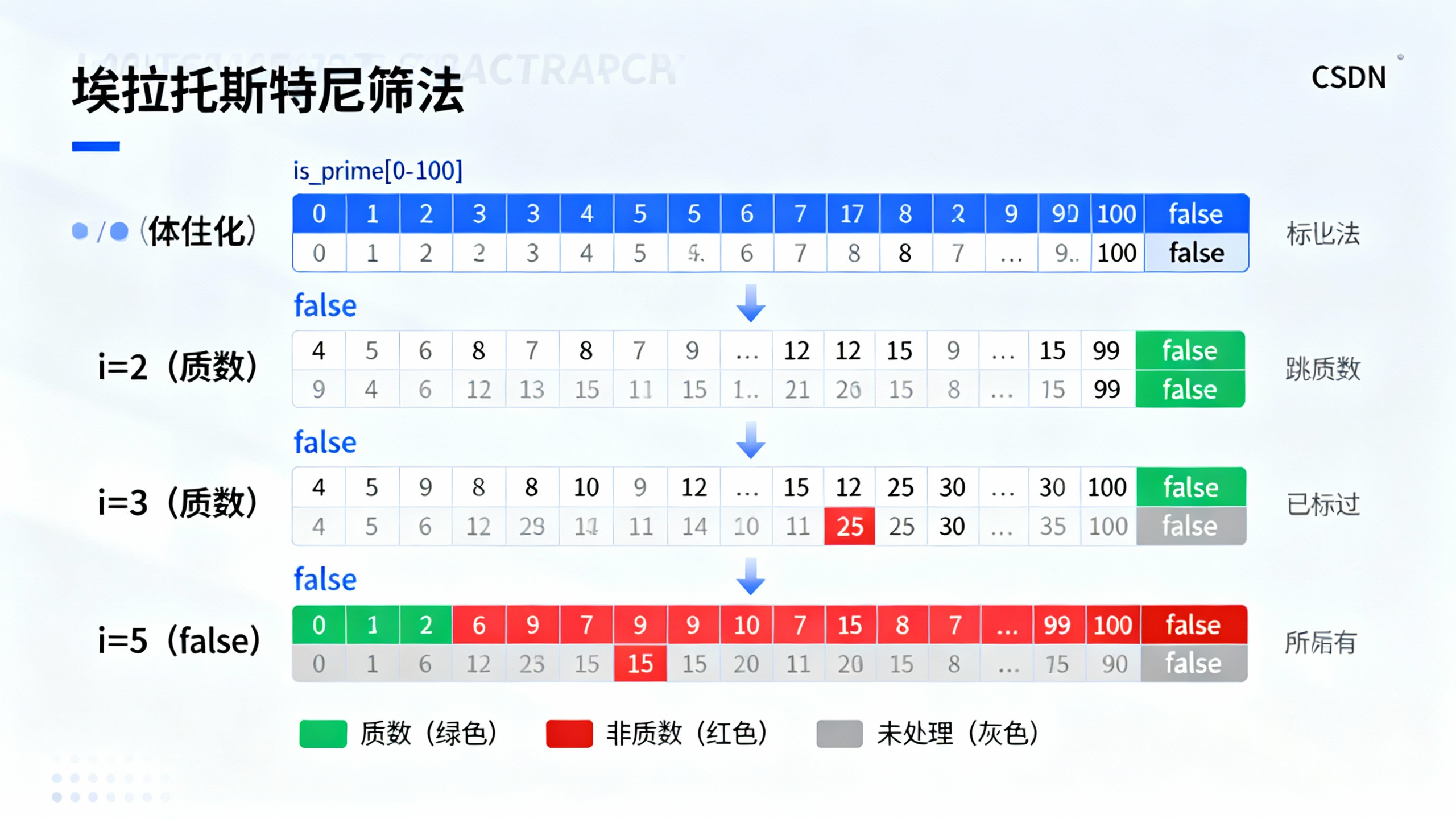
当需要判断的范围扩大(比如2-100万),逐个判断法的效率会明显下降。此时推荐使用埃拉托斯特尼筛法——一种通过"标记非质数"来快速筛选质数的算法,时间复杂度为O(n log log n),远优于逐个判断法。
筛法实现代码(2-100示例)
#include <stdio.h>
#include <stdbool.h> // 用于bool类型
int main() {
bool is_prime[101]; // 数组下标对应数字,值为true表示是质数
int count = 0;
// 初始化:默认所有数都是质数
for (int i = 0; i <= 100; i++) {
is_prime[i] = true;
}
is_prime[0] = is_prime[1] = false; // 0和1不是质数
// 筛法核心:标记非质数
for (int i = 2; i * i <= 100; i++) {
if (is_prime[i]) { // 如果i是质数,标记i的倍数为非质数
for (int j = i * i; j <= 100; j += i) {
is_prime[j] = false;
}
}
}
// 统计并输出质数
printf("2-100 之间的质数有:\n");
for (int i = 2; i <= 100; i++) {
if (is_prime[i]) {
printf("%d ", i);
count++;
}
}
printf("\n2-100 之间共有 %d 个质数\n", count);
return 0;
}筛法核心逻辑拆解
- 初始化标记数组:创建一个布尔数组
is_prime,下标代表数字,初始值全部设为true(默认都是质数),再手动将0和1标记为false(非质数)。 - 标记非质数:从2开始遍历到√100(即10):
- 如果当前数字
i是质数(is_prime[i]为true),则将i的所有倍数(从i*i开始,因为更小的倍数已经被之前的质数标记过)标记为false。 - 例如
i=2时,标记4、6、8…100为非质数;i=3时,标记9、12、15…99为非质数,以此类推。
- 如果当前数字
- 收集结果:遍历数组,所有仍为
true的下标就是质数。
筛法优势直观感受
以100为例可能看不出明显差异,但如果计算100万以内的质数:
- 逐个判断法需要对每个数执行多次取余运算,耗时较长;
- 筛法只需一次遍历标记,后续直接读取结果,效率提升几十倍甚至上百倍。
两种方法的适用场景对比

在这里插入图片描述
算法 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|
逐个判断法 | 实现简单,内存占用小(无需数组) | 大范围计算时效率低 | 小范围(如1000以内)质数判断,或偶尔需要判断单个质数 |
埃拉托斯特尼筛法 | 批量计算效率极高,时间复杂度低 | 需占用一定内存(存储标记数组) | 大范围(如1万以上)质数批量筛选,或频繁需要查询质数的场景 |
实战拓展:代码可优化方向
- 内存优化:筛法中可使用位运算替代
bool数组(1个字节存储8个标记),进一步减少内存占用。 - 范围扩展:若需要计算更大范围的质数(如1000万),可动态分配内存(
malloc)创建标记数组,避免栈溢出。 - 并行计算:在超大范围(如10亿以上)场景,可结合多线程对筛法进行并行优化,将不同区间分配给多个线程处理。
通过本文的两种算法实现,你不仅能解决"2-100之间有多少个质数"这个具体问题,更能理解质数判断的核心逻辑与效率优化思路。在实际开发中,选择合适的算法往往比盲目编码更重要——这也是编程思维的核心体现。
如果需要进一步理解筛法的执行步骤,或者想尝试更大范围的质数计算,欢迎在评论区交流!
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-12-09,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

