PTA L1-009 满分踩坑笔记,带负数、爆 long、0 分子、测试点一次讲透!
PTA L1-009 满分踩坑笔记,带负数、爆 long、0 分子、测试点一次讲透!

Extreme35
发布于 2025-12-23 18:08:29
发布于 2025-12-23 18:08:29
题目简介及链接:
L1-009 N个数求和
本题的要求很简单,就是求N个数字的和。麻烦的是,这些数字是以有理数分子/分母的形式给出的,你输出的和也必须是有理数的形式。
输入格式:
输入第一行给出一个正整数N(≤100)。随后一行按格式a1/b1 a2/b2 ...给出N个有理数。题目保证所有分子和分母都在长整型范围内。另外,负数的符号一定出现在分子前面。
输出格式:
输出上述数字和的最简形式 —— 即将结果写成整数部分 分数部分,其中分数部分写成分子/分母,要求分子小于分母,且它们没有公因子。如果结果的整数部分为0,则只输出分数部分。
输入样例1:
5
2/5 4/15 1/30 -2/60 8/3输出样例1:
3 1/3题目思考
- 这里看题目可以得到分子分母都不会超过长整型,也就是
long int,但总共会有100个分数,这时候就又有超出范围的风险了,所以写代码时能考虑到的超范围的情况,最好还是顺便处理。 - 要求结果写成
整数部分 分数部分,那在最后输出的时候大概率需要进行条件判断,而且需要约分到最简形式,先有个心里准备。 - 看到样例中分数有负有正,这时候就需要对负数进行额外思考。
- 而且分数中,不明确样例中是否会有分子为0的情况,故也需要进行思考判断。
- 而且每次分数的个数会不一样,这时候如果你想一次性将所有分数存起来然后处理,个人认为不理智,最好就是输入一个处理一个,而且代码好想也好写。
思路
顺着思考现在应该大致就有了一个整体思路:
- 首先,每输入一个分数,就加到最后的输出中,但如果这个分数不合理:
分子为0或者分母为0,那更好了,直接可以跳过然后加下一个分数。 - 每次加到最后的输出时,如果这时候是100个数,那极有可能会超出长整型的范围,所以我们每一步运算的时候都需要进行约分,也就是找最大公约数、最小公倍数。
- 按照最简单的通分运算,每次找到两个分母的最小公倍数,然后分子进行通分相加,防止下一次超出范围,运算完后进行化简。
在有这个最简单的思路后就可以尝试写代码了。
代码实现
main函数流程
- 首先需要定义变量,也就是输入输出的分子分母。
- 随后就是对每一个输入的分数进行相加。
- 完成后对结果进行判断兵输出
这里给出一个示例的伪代码(完整代码在文章最后,可直接运行):
int main()
{
//分数个数
int num = 0;
scanf("%d", &num);
//求和后结果的初始分子分母
long up_sum = 0;
long down_sum = 1;
//初始化输入的分子分母
long up = 0;
long down = 0;
while (num)
{
//接收每一个输入的分数
scanf("%ld%*c%ld", &up, &down);
//这里就是对分数进行相加的流程
//后面部分给出
todo!!!
num--;
}
//对结果输出进行判断
if () {}
else {}
return 0;
}这里可以看到代码实现对输入进行了赋值忽略,示例在输入时是按照 分子/分母 的形式,现在我们只需要分子与分母,故可以采用两种方式:
- 一种是按照格式进行读取,也就是
scanf("%ld/%ld", &up, &down); - 第二种就是我写的这种通用方式,
scanf()提供了⼀个赋值忽略符(assignment suppression character)*。 只要把*加在任何占位符的百分号后⾯,该占位符就不会返回值,解析后将被丢弃。
分数相加函数实现
- 这里就是每次对分数进行相加,最后将结果带回的函数实现。
- 这里有个小细节,每次相加后都会有新的分子分母,这时候是两个值,而C语言除非返回数组的指针,不然不可能实现,但数组又会把这个题搞复杂,所以这里选择将结果的
分子分母地址传入函数,通过指针访问变量地址进行修改,从而将函数内相加后的分子分母进行带出来。 - 在运算时还需考虑负数的情况,且这个题没有明确告诉你
负号在分子还是分母,所以两种情况都需要考虑(之前有的题就遇到过分母带负号)。可以允许分子有负号,但分母有负号是一定需要先进行处理,最多也就这么几种情况:- 分子负,分母正,可以不管。
- 分子正,分母负,交换负号。
- 同时为负,相当于同为正,直接去掉两个负号。
- 在约分寻找最大公约数和最小公倍数的时候,还特别需要考虑是否会超出范围的问题,这里推荐大家学习一下
辗转相除法,非常好用一个算法。
这里给出实现的伪代码:
//对两个分数进行求和,并带出求和后的值供后续使用
void add_sum(long up, long down, long* up_sum, long* down_sum)
{
//处理负号可能在分母的情况
if (up < 0 && down < 0)
{
up = abs(up);
down = abs(down);
}
else if (up > 0 && down < 0)
{
up = (-1) * up;
down = abs(down);
}
long new_down = Lcm(down, *down_sum);//两个分数通分后 未约分的新分母
long new_up = up * (new_down / down) + *up_sum * (new_down / *down_sum);//未约分的新分子
long gcd = Gcd(new_down, abs(new_up));//未约分的新分母分子最大公约数
//结果约分
*up_sum = new_up / gcd;
*down_sum = new_down / gcd;
}此处通分我是采用通分至最小公倍数,而不是直接相乘,这里想简单点可以尝试直接相乘,实现起来都不难。
其中Gcd与Lcm为辗转相除法求最大公约数最小公倍数的函数实现,这里给出具体代码,讲解可以参考解题—求两数的最大公约数与最小公倍数 #辗转相除法这篇文章,代码实现如下:
//两数的最大公约数
long Gcd(long a,long b)
{
//核心逻辑:当b不为0时,循环替换a与b,直至b为0,则m就是最大公约数
while (b != 0)
{
int temp = b;//临时存储b的值,防止后续被覆盖
b = a % b;//a对b取余进行更新
a = temp;//用原来的b更新a
}
return a;//当循环停止时,即计算下去无余数时此时的被除数便为最大公约数
}
//最小公倍数
long Lcm(long a, long b)
{
return ((a / Gcd(a, b)) * b);//防止溢出
}这里怕求最小公倍数时超出范围,故没有使用两数相乘除以最大公约数,而是先约分再进行相乘。
判断逻辑
这部分就比较简单,首先将假分数化成带分数的形式输出,其次将结果为0的直接输出0。实现如下:
if (abs(up_sum) >= down_sum && up_sum % down_sum != 0)
printf("%ld %ld/%ld", abs(up_sum / down_sum), up_sum % down_sum, down_sum);
else if(up_sum % down_sum == 0)
printf("%ld", up_sum / down_sum);
else if(up_sum != 0)
printf("%ld/%ld", up_sum, down_sum);
else
printf("0");以上就是整个题目的全部实现逻辑及代码.
完整代码
#include<stdio.h>
#include<math.h>
//两数的最大公约数
long Gcd(long a,long b)
{
//核心逻辑:当b不为0时,循环替换a与b,直至b为0,则m就是最大公约数
while (b != 0)
{
int temp = b;//临时存储b的值,防止后续被覆盖
b = a % b;//a对b取余进行更新
a = temp;//用原来的b更新a
}
return a;//当循环停止时,即计算下去无余数时此时的被除数便为最大公约数
}
//最小公倍数
long Lcm(long a, long b)
{
return ((a / Gcd(a, b)) * b);//防止溢出
}
//对两个分数进行求和,并带出求和后的值供后续使用
void add_sum(long up, long down, long* up_sum, long* down_sum)
{
if (up < 0 && down < 0)
{
up = abs(up);
down = abs(down);
}
else if (up > 0 && down < 0)
{
up = (-1) * up;
down = abs(down);
}
long new_down = Lcm(down, *down_sum);//两个分数通分后 新分母
long new_up = up * (new_down / down) + *up_sum * (new_down / *down_sum);
long gcd = Gcd(new_down, abs(new_up));
*up_sum = new_up / gcd;
*down_sum = new_down / gcd;
}
int main()
{
//分数个数
int num = 0;
scanf("%d", &num);
//求和的初始分子分母
long up_sum = 0;
long down_sum = 1;
//初始化输入的分子分母
long up = 0;
long down = 0;
while (num)
{
//接收每一个输入的分数
scanf("%ld%*c%ld", &up, &down);
if(up!=0&&down!=0)
add_sum(up, down, &up_sum, &down_sum);
num--;
}
if (abs(up_sum) >= down_sum && up_sum % down_sum != 0)
printf("%ld %ld/%ld", abs(up_sum / down_sum), up_sum % down_sum, down_sum);
else if(up_sum % down_sum == 0)
printf("%ld", up_sum / down_sum);
else if(up_sum != 0)
printf("%ld/%ld", up_sum, down_sum);
else
printf("0");
return 0;
}结果
在PTA N个数求和中提交代码查看结果:
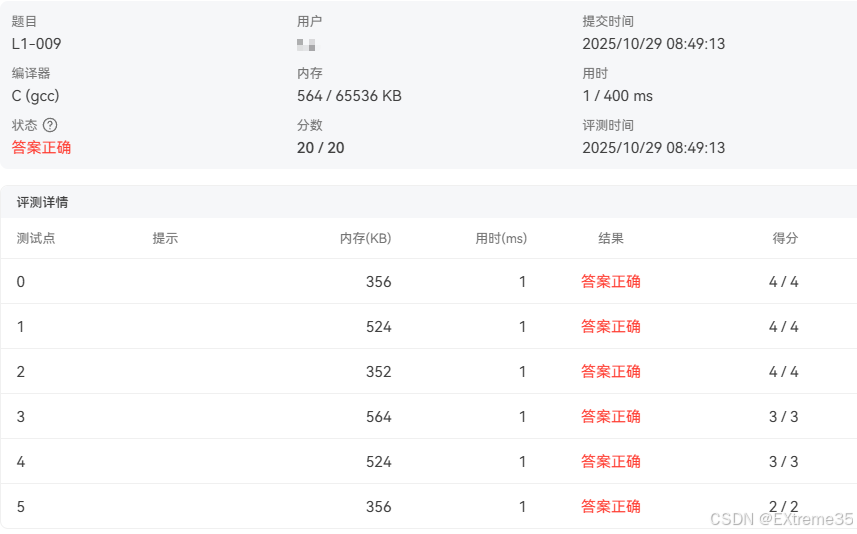
在这里插入图片描述
坑点:这里测试点0、1、2就是三个样例,3、4应该是分母分子混合为负的情况,5就是最后输出为0的情况。
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-10-29,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

