轮转数组——深度解剖逆转算法的奥秘

◆ 博主名称: 小此方-CSDN博客
大家好,欢迎来到小此方的博客。
🔥个人专栏:《C语言》_小此方的博客-CSDN博客
🔥 努力成就未来,代码改变世界,相信我有一天也能成为改变世界的那个人
先看题:
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出:
[5,6,7,1,2,3,4]
解释:
向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]一,暴力解
➤看到这道题目,想必大家第一时间会想到最暴力的方法:
存储最后一个元素,然后将所有元素向后移动一格,最后将这个元素放在数组的第一位。
while(k)
{
int a = nums[numsSize-1];
int i=numsSize-2;
while(i>=0)
{
nums[i+1] = nums[i];
i--;
}
nums[0]=a;
k--;
}但,事实上,这个算法的时间复杂度是O(N),有没有其他更厉害的方法?
二,创建新数组
int arr[numsSize] ;
int i=0;
int j=k;
while(i<k&&j>0)
{
arr[i]=nums[numsSize-j];
i++;
j--;
}
int n=k;
int m=0;
while(m < numsSize-k)
{
arr[n]=nums[m];
n++;
m++;
}
int q=0;
while(q<numsSize)
{
nums[q] = arr[q];
q++;
}➤ 通过观察,我们不难发现,轮转后的数组有两部分组成,以此为例:
4,5,6,7,1,2,3➤ 我们可以将它拆分成5,6,7和1,2,3,4两个部分。因此,我们想到了创建一个新的数组的方法,如图:
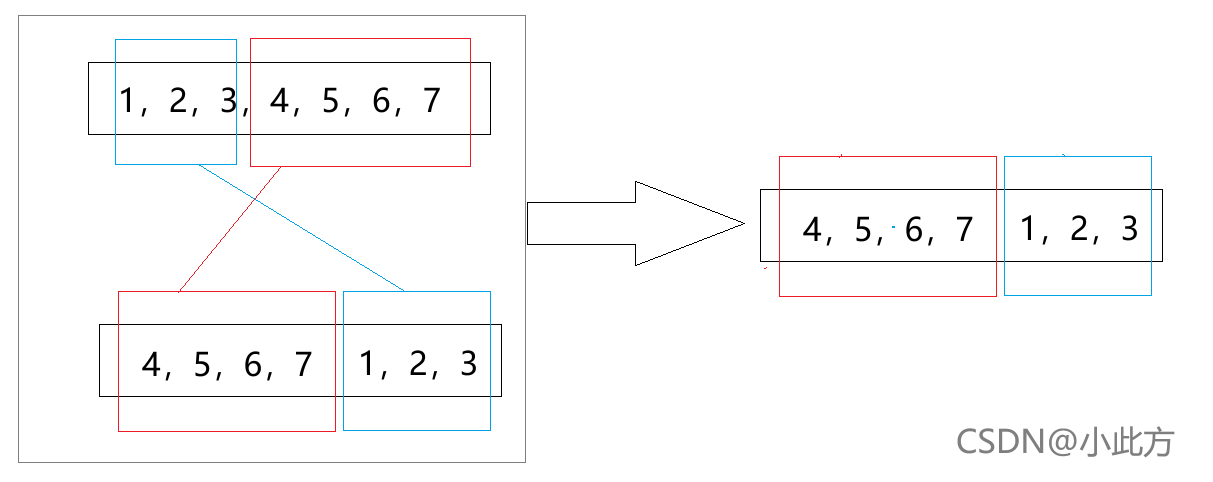
三,翻转算法
//算法二
//先让前n-k个数字反转
//0------k-1
k = k % numsSize; // 关键:处理 k 大于数组长度的情况
if (k == 0)
return; // 如果不需要旋转,直接返回
int front01=0;
int end01 = numsSize-k-1;
while(front01<=end01)
{
int mid01 = nums[front01];
nums[front01] = nums[end01];
nums[end01] = mid01;
front01++;
end01--;
}
//再让后k个数字反转
int front02 = numsSize-k;
int end02 = numsSize-1;
while(front02<=end02)
{
int mid02=nums[front02];
nums[front02]=nums[end02];
nums[end02]=mid02;
front02++;
end02--;
}
//整体再反转
int front = 0;
int end = numsSize-1;
while(front<=end)
{
int mid=nums[front];
nums[front]=nums[end];
nums[end]= mid;
front++;
end--;
}✦ 暴击消耗的时间复杂度高
✦ 创建新数组消耗的空间复杂度高
那么,在“创建新数组的思想”基础之上,有没有能原地修改的办法?
翻转算法能解决这个问题。

一,翻转算法的步骤
✦ 先对前面一部分(前)数据翻转,
✦ 再对后面一部分(后)数据翻转,
✦ 最后在整体翻转。
“我们如何定义一部分?”先不急——,我们先来讲一讲:翻转算法的方向问题:
二,左旋与右旋?
右旋转定义:元素向右移动,右边的元素从尾部回到头部
左旋转定义:元素向左移动,左边的元素从头部回到尾部

如图,如果数组向右旋转,那么数组后面的数字会依次被放置在数组前面,数组前面的元素依次向后移动一位。————即轮转k次,
✦ 先对前面一部分(前)数据翻转, ✦ 再对后面一部分(后)数据翻转,
这里就指一部分(前)=k;一部分(后)=n-k;
反之,左旋:一部分(前)=n-k;一部分(后)=k;
简单来说:
- 如果k表示右旋步数,就反转前 n-k 个
- 如果k表示左旋步数,就反转前 k 个
数学上的重要发现:
右旋k位 = 左旋(n-k)位 左旋k位 = 右旋(n-k)位
三,怎么想到的
这种思路来源于一个已知的数学事实:
对序列
(X Y),想变成(Y X),可以:
- 反转 X → X'
- 反转 Y → Y'
- 反转整体 (X' Y') → Y X
在字符串旋转、链表旋转等问题中都有类似技巧。 它本质上是利用了反转操作的双重应用可以重置部分顺序的性质。
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-11-08,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录


