构建AI智能体:超参数如何影响大模型?通俗讲解原理、作用与实战示例
原创构建AI智能体:超参数如何影响大模型?通俗讲解原理、作用与实战示例
原创
未闻花名
发布于 2025-12-28 10:41:25
发布于 2025-12-28 10:41:25
一、什么是超参数
超参数是机器学习模型在训练开始前需要设定的配置参数,它们不是从数据中学习得到的,而是用来控制学习过程的指导参数,通俗的理解,想象一下,我们在骑自行车时,需要先进行一些调整,比如座椅高度、把手位置和轮胎气压。这些设置不是我们在骑行过程中自动学会的,而是我们在开始前手动调整的。超参数就像这些设置,它们是机器学习模型在训练开始前,由我们人工设定的参数,用来控制模型如何学习。
再比如我们学习烹饪一道新菜,菜谱说明要用适量的盐、中火烹饪、几分钟的时间。这些"适量"、"中火"、"几分钟"就是烹饪中的超参数,它们不是食材本身,但决定了最终菜肴的味道和质量。在机器学习中,超参数就是这些烹饪设置,它们在模型训练开始前由我们手动设定,控制着模型如何从数据中学习。
与超参数相对的是模型参数,它们是模型在训练过程中从数据中自动学到的,比如神经网络的权重。简单来说:
- 超参数:训练前设定,影响学习过程。
- 模型参数:训练中自动学习,决定模型预测能力。
比如教一个孩子认字:
- 超参数:每天学习多长时间、每次学几个字、复习频率
- 模型参数:孩子大脑中形成的汉字记忆和识别能力
二、超参数的基础原理
模型的学习过程,本质上是一个优化问题:模型通过反复调整内部参数,来最小化预测错误。超参数就是这个优化过程的指导手册,控制着学习的速度、方式和稳定性。
核心原理:
- 超参数定义了模型的学习规则。例如,学习率决定了模型每次更新参数的步长。如果步长太大,模型可能跨过最优解;如果步长太小,学习会非常缓慢。
- 没有超参数,模型就像一辆没有方向盘的汽车,它可能永远找不到正确的路径。
三、超参数调优流程
1. 流程图
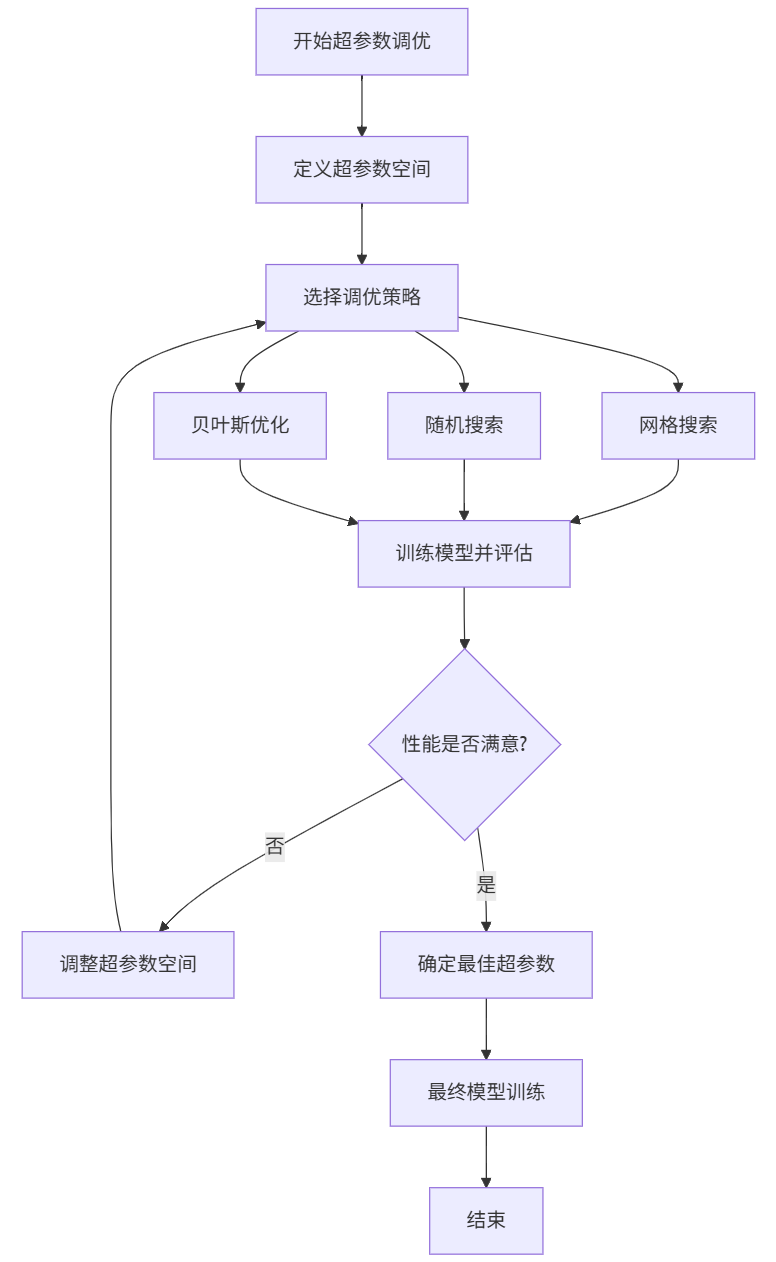
2. 流程说明
- 1. 定义搜索范围
- 确定要调整哪些参数(如学习率、批量大小等)
- 设定每个参数的尝试取值范围
- 2. 选择调优方法
- 网格搜索:尝试所有参数组合(全面但耗时)
- 随机搜索:随机尝试部分组合(快速高效)
- 贝叶斯优化:智能选择下一个尝试组合(最先进)
- 3. 训练与评估循环
- 用选定参数训练模型
- 评估模型性能(准确率、损失值等)
- 4. 性能检查
- 检查当前性能是否满意
- 如果不满意,则调整搜索范围,继续尝试
- 如果满意,则进入下一步
- 5. 确定最佳参数
- 选择性能最好的参数组合
- 用最佳参数重新训练最终模型
流程总结:
- 自动试错,逐步优化,通过系统化的尝试和评估,找到让模型表现最好的参数设置,避免手动调参的盲目性。
- 整个过程就像寻找最佳烹饪配方:尝试不同配料比例 → 品尝效果 → 调整配方 → 直到找到最美味的组合。
四、常见超参数详解
超参数的种类很多,以下以最常见的几种为例,解释它们如何影响模型,尤其是大模型:
1. 学习率
- 作用:学习率控制模型参数更新的步长,即每次更新参数的幅度,是影响训练稳定性和收敛速度的最关键因素。
- 示例:假设我们在下山途中(寻找最低点),学习率就像我们每步的步长:
- 步长太大(高学习率):可能一步跨过山谷,无法收敛。
- 步长太小(低学习率):下山太慢,耗时过长。
- 对大模型的影响:大模型参数巨多,学习率设置不当会导致训练不稳定或资源浪费,模型的训练中,学习率需要精心调整以避免梯度爆炸。
2. 批量大小
- 作用:批量大小决定了每次参数更新时使用的样本数量,影响训练速度、内存使用和模型泛化能力。
- 示例:比如正在背单词。
- 批量小(如每次1个单词):更新频繁,但可能受噪声影响。
- 批量大(如每次100个单词):更稳定,但需要更多内存。
- 对大模型的影响:大模型训练通常使用大规模数据,批量大小会影响训练速度和泛化能力。批量太大会导致内存不足,太小则训练效率低。
3. 迭代次数
- 作用:定义模型遍历整个数据集的次数。
- 示例:复习一本书。
- 次数太少:知识不牢固(欠拟合)。
- 次数太多:浪费时间甚至记混(过拟合)。
- 对大模型的影响:大模型训练成本高,迭代次数需平衡效果和资源。
4. 隐藏层大小
- 作用:控制神经网络的复杂度。
- 示例:大脑的神经元数量。
- 神经元太少:模型简单,无法学习复杂模式。
- 神经元太多:模型复杂,可能过拟合。
- 对大模型的影响:大模型通常有数十亿参数,隐藏层大小直接影响模型能力。
五、超参数的意义
- 效率与性能:大模型训练需要大量计算资源(如GPU)。合适的超参数可以加速训练,提升准确率。例如,谷歌的BERT模型通过超参数调优,在自然语言处理任务中实现了突破。
- 泛化能力:超参数帮助模型避免过拟合,解决在训练数据上表现好,但测试数据上差的问题。这对于大模型尤其重要,因为它们容易记住数据中的噪声。
- 资源优化:错误的超参数可能导致训练失败或资源浪费。例如,学习率过高会使损失值震荡,无法收敛。
六、超参数调优示例
我们以线性回归为例,演示超参数(学习率和迭代次数)对模型训练的影响。我们将使用自定义数据,并绘制损失函数随迭代次数的变化曲线,以及模型参数更新的路径。
示例步骤:
- 1. 生成示例数据:使用一个简单的线性关系,加上一些噪声。
- 2. 定义线性回归模型和损失函数(均方误差)。
- 3. 使用梯度下降法训练模型,并记录每次迭代的损失值。
- 4. 绘制不同学习率下损失函数的变化曲线,以及参数更新的路径。
1. 数据准备
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 设置中文字体,避免中文乱码
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 生成示例数据 - 房价预测问题
np.random.seed(42)
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 2 * X.flatten() + 1 + np.random.normal(0, 2, 100)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
print("数据准备完成!样本数量:", len(X_train))2. 演示学习率对梯度下降的影响
def gradient_descent_visualization():
"""演示不同学习率对梯度下降过程的影响"""
# 模拟梯度下降过程
def simple_gradient_descent(X, y, learning_rate, iterations):
m, b = 0, 0 # 初始参数
n = len(X)
loss_history = []
param_history = []
for i in range(iterations):
# 计算梯度
y_pred = m * X + b
dm = (-2/n) * np.sum(X * (y - y_pred)) # 对m的梯度
db = (-2/n) * np.sum(y - y_pred) # 对b的梯度
# 更新参数
m = m - learning_rate * dm
b = b - learning_rate * db
# 记录损失和参数
loss = np.mean((y - y_pred) ** 2)
loss_history.append(loss)
param_history.append((m, b))
return loss_history, param_history
# 不同学习率的实验
learning_rates = [0.001, 0.01, 0.1, 0.5]
colors = ['blue', 'green', 'orange', 'red']
labels = ['学习率=0.001(过小)', '学习率=0.01(合适)', '学习率=0.1(稍大)', '学习率=0.5(过大)']
plt.figure(figsize=(15, 5))
# 子图1:损失函数下降曲线
plt.subplot(1, 2, 1)
for lr, color, label in zip(learning_rates, colors, labels):
loss_history, _ = simple_gradient_descent(X_train.flatten(), y_train, lr, 100)
plt.plot(loss_history, color=color, label=label, linewidth=2)
plt.xlabel('迭代次数')
plt.ylabel('损失值 (MSE)')
plt.title('不同学习率下的损失函数下降过程')
plt.legend()
plt.grid(True, alpha=0.3)
# 子图2:参数更新路径(等高线图)
plt.subplot(1, 2, 2)
# 生成损失函数的等高线
m_range = np.linspace(0, 4, 100)
b_range = np.linspace(-2, 4, 100)
M, B = np.meshgrid(m_range, b_range)
# 计算每个点的损失
Z = np.zeros_like(M)
for i in range(len(m_range)):
for j in range(len(b_range)):
y_pred = M[j,i] * X_train.flatten() + B[j,i]
Z[j,i] = np.mean((y_train - y_pred) ** 2)
# 绘制等高线
contour = plt.contour(M, B, Z, levels=20, alpha=0.5)
plt.clabel(contour, inline=True, fontsize=8)
# 绘制不同学习率的参数更新路径
for lr, color, label in zip(learning_rates, colors, labels):
_, param_history = simple_gradient_descent(X_train.flatten(), y_train, lr, 20)
m_vals = [p[0] for p in param_history]
b_vals = [p[1] for p in param_history]
plt.plot(m_vals, b_vals, 'o-', color=color, label=label, markersize=4)
plt.xlabel('斜率 (m)')
plt.ylabel('截距 (b)')
plt.title('不同学习率下的参数更新路径')
plt.legend()
plt.tight_layout()
plt.show()
# 运行可视化
print("生成学习率对比图...")
gradient_descent_visualization()输出结果:
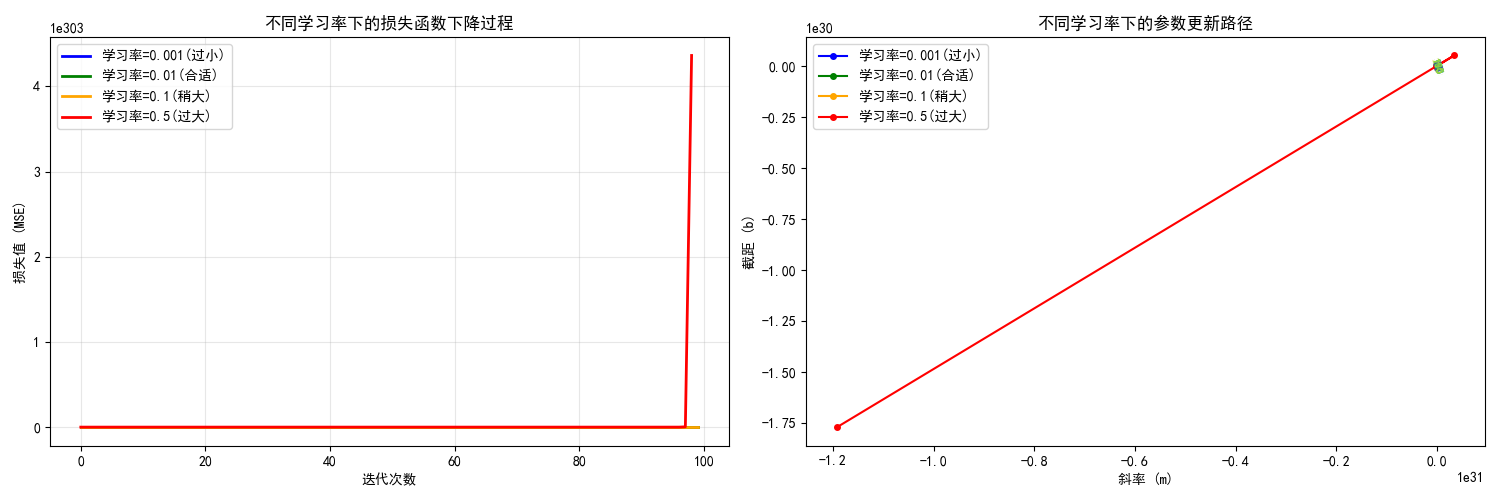
- 图片内容:
- 左图:显示不同学习率下损失函数随迭代次数的下降曲线
- 右图:在参数空间(斜率m vs 截距b)中显示参数更新的路径轨迹
- 图片意义:
- 学习率控制参数更新的步长,直接影响梯度下降的收敛行为
- 通过模拟真实的梯度下降过程,记录每次迭代的损失值和参数值
- 达到的效果:
- 学习率过小(0.001):收敛缓慢,需要很多次迭代才能到达最优点
- 学习率合适(0.01):平稳快速收敛到最优点
- 学习率稍大(0.1):在最优值附近震荡,但最终能收敛
- 学习率过大(0.5):严重震荡甚至发散,无法收敛
3. 批量大小对训练的影响
def batch_size_impact():
"""演示批量大小对训练稳定性和速度的影响"""
def mini_batch_gradient_descent(X, y, batch_size, learning_rate=0.01, epochs=50):
m, b = 0, 0
n = len(X)
loss_history = []
for epoch in range(epochs):
# 随机打乱数据
indices = np.random.permutation(n)
X_shuffled = X[indices]
y_shuffled = y[indices]
epoch_loss = 0
# 小批量处理
for i in range(0, n, batch_size):
X_batch = X_shuffled[i:i+batch_size]
y_batch = y_shuffled[i:i+batch_size]
batch_len = len(X_batch)
# 计算梯度
y_pred = m * X_batch + b
dm = (-2/batch_len) * np.sum(X_batch * (y_batch - y_pred))
db = (-2/batch_len) * np.sum(y_batch - y_pred)
# 更新参数
m = m - learning_rate * dm
b = b - learning_rate * db
epoch_loss += np.mean((y_batch - y_pred) ** 2)
loss_history.append(epoch_loss / (n // batch_size))
return loss_history
# 不同批量大小的实验
batch_sizes = [1, 10, 50, 100] # 批量大小从1(随机梯度下降)到100(批量梯度下降)
colors = ['red', 'orange', 'green', 'blue']
labels = ['批量大小=1(SGD)', '批量大小=10', '批量大小=50', '批量大小=100(BGD)']
plt.figure(figsize=(12, 5))
for bs, color, label in zip(batch_sizes, colors, labels):
loss_history = mini_batch_gradient_descent(X_train.flatten(), y_train, bs)
plt.plot(loss_history, color=color, label=label, linewidth=2)
plt.xlabel('训练轮次 (Epoch)')
plt.ylabel('损失值 (MSE)')
plt.title('不同批量大小对训练稳定性的影响')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print("生成批量大小对比图...")
batch_size_impact()输出结果:
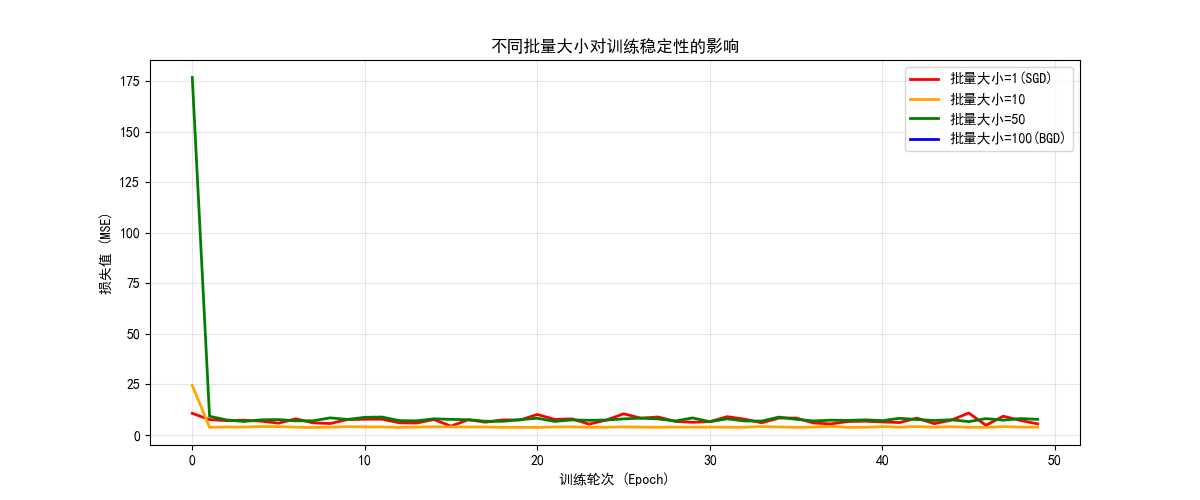
- 图片内容:
- 显示不同批量大小下,损失函数随训练轮次的变化趋势
- 图片意义:
- 批量大小决定了每次参数更新时使用的样本数量
- 小批量带来更多的噪声但更新频繁,大批量更稳定但更新缓慢
- 达到的效果:
- 批量大小=1(随机梯度下降):波动很大,但收敛速度快
- 批量大小=10:相对稳定,收敛良好
- 批量大小=50:更加平滑,收敛稳定
- 批量大小=100(批量梯度下降):最平滑但可能陷入局部最优
4. 模型复杂度对模型拟合的影响
def model_complexity_demo():
"""演示模型复杂度(多项式次数)对拟合效果的影响"""
degrees = [1, 3, 10, 15] # 不同的多项式次数
colors = ['blue', 'green', 'orange', 'red']
plt.figure(figsize=(15, 10))
train_errors = []
test_errors = []
for i, degree in enumerate(degrees):
plt.subplot(2, 2, i+1)
# 创建多项式回归模型
poly_features = PolynomialFeatures(degree=degree, include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([
("poly_features", poly_features),
("lin_reg", linear_regression),
])
# 训练模型
pipeline.fit(X_train, y_train)
# 预测
X_range = np.linspace(0, 10, 300).reshape(-1, 1)
y_range_pred = pipeline.predict(X_range)
# 计算误差
y_train_pred = pipeline.predict(X_train)
y_test_pred = pipeline.predict(X_test)
train_error = mean_squared_error(y_train, y_train_pred)
test_error = mean_squared_error(y_test, y_test_pred)
train_errors.append(train_error)
test_errors.append(test_error)
# 绘制结果
plt.scatter(X_train, y_train, color='blue', alpha=0.6, label='训练数据')
plt.scatter(X_test, y_test, color='red', alpha=0.6, label='测试数据')
plt.plot(X_range, y_range_pred, color='black', linewidth=2,
label=f'多项式次数={degree}')
plt.xlabel('房屋面积')
plt.ylabel('房价')
plt.title(f'多项式次数={degree}\n训练误差: {train_error:.2f}, 测试误差: {test_error:.2f}')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 绘制误差随复杂度变化的曲线
plt.figure(figsize=(10, 6))
plt.plot(degrees, train_errors, 'o-', color='blue', label='训练误差', linewidth=2)
plt.plot(degrees, test_errors, 'o-', color='red', label='测试误差', linewidth=2)
plt.xlabel('模型复杂度(多项式次数)')
plt.ylabel('均方误差 (MSE)')
plt.title('模型复杂度与过拟合现象')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print("生成模型复杂度对比图...")
model_complexity_demo()输出结果:
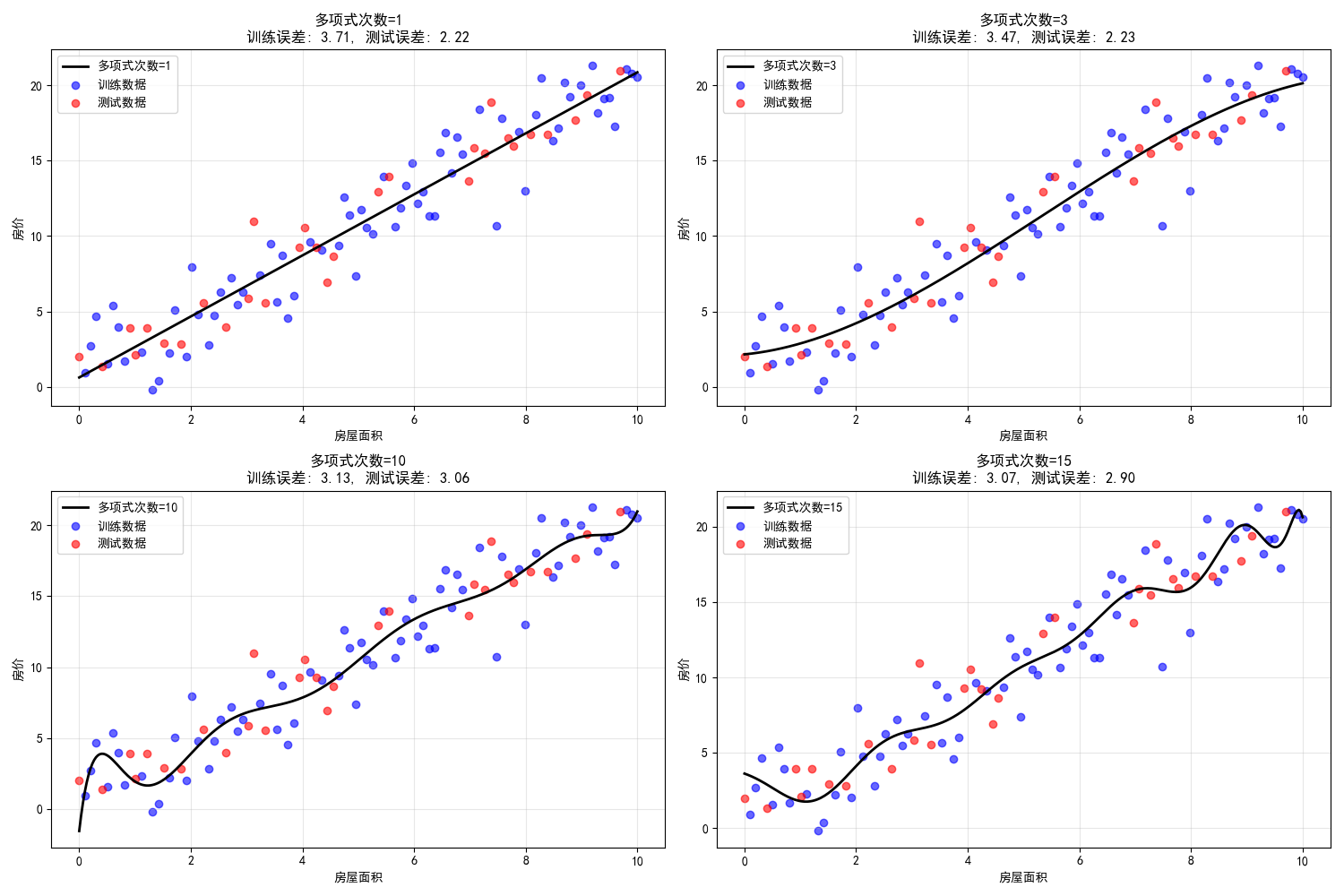
训练误差和测试误差汇总图:
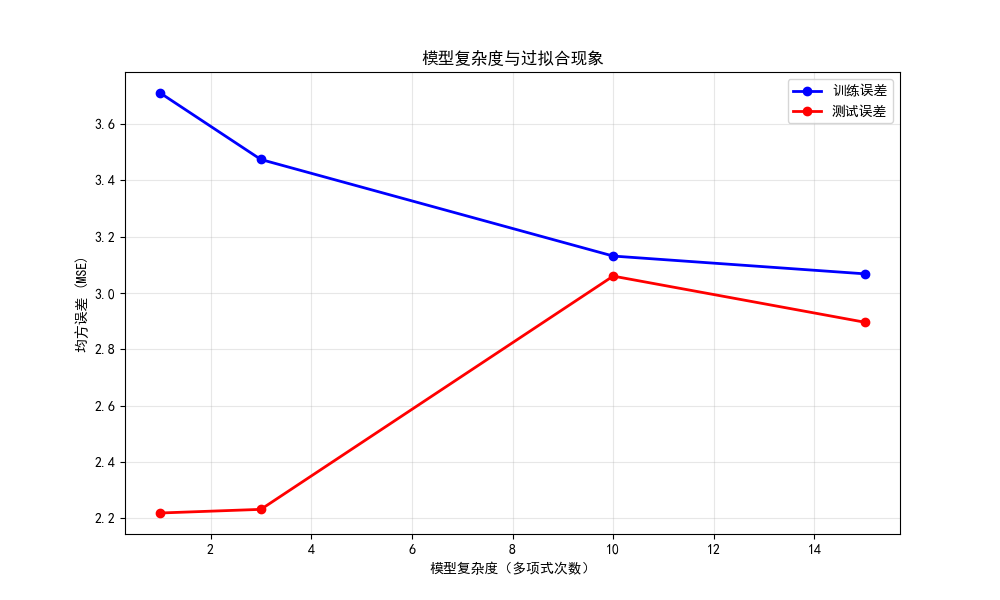
- 图片内容:
- 上排4个子图:显示不同多项式次数下模型对数据的拟合情况
- 下排1个总图:显示训练误差和测试误差随模型复杂度的变化
- 图片意义:
- 模型复杂度(如多项式次数)是重要的超参数,控制模型的拟合能力
- 复杂度不足导致欠拟合,复杂度过高导致过拟合
- 达到的效果:
- 次数=1(线性):欠拟合,无法捕捉数据模式
- 次数=3:拟合良好,泛化能力强
- 次数=10:开始过拟合,对噪声敏感
- 次数=15:严重过拟合,完美拟合训练数据但泛化差
5. 超参数调优综合评估
def hyperparameter_tuning_demo2():
"""综合演示超参数调优过程"""
# 网格搜索超参数
learning_rates = [0.001, 0.01, 0.1]
batch_sizes = [5, 20, 50]
results = []
plt.figure(figsize=(12, 8))
for i, lr in enumerate(learning_rates):
for j, bs in enumerate(batch_sizes):
# 模拟训练过程
loss_history = []
m, b = 0, 0
n = len(X_train)
for epoch in range(30):
indices = np.random.permutation(n)
X_shuffled = X_train.flatten()[indices]
y_shuffled = y_train[indices]
epoch_loss = 0
for k in range(0, n, bs):
X_batch = X_shuffled[k:k+bs]
y_batch = y_shuffled[k:k+bs]
batch_len = len(X_batch)
y_pred = m * X_batch + b
dm = (-2/batch_len) * np.sum(X_batch * (y_batch - y_pred))
db = (-2/batch_len) * np.sum(y_batch - y_pred)
m = m - lr * dm
b = b - lr * db
epoch_loss += np.mean((y_batch - y_pred) ** 2)
loss_history.append(epoch_loss / (n // bs))
# 计算最终模型在测试集上的表现
y_test_pred = m * X_test.flatten() + b
test_error = mean_squared_error(y_test, y_test_pred)
results.append((lr, bs, test_error, loss_history))
# 格式化测试误差显示
if test_error > 1000:
# 使用科学计数法显示大数值
error_str = f"{test_error:.2e}"
color = 'red' # 标记过大的误差为红色
size_tag = "(很大)"
elif test_error > 100:
error_str = f"{test_error:.1f}"
color = 'orange' # 标记较大的误差为橙色
size_tag = "(较大)"
else:
error_str = f"{test_error:.2f}"
color = 'black' # 正常误差为黑色
size_tag = ""
# 绘制损失曲线
plt.subplot(3, 3, i*3 + j + 1)
plt.plot(loss_history, linewidth=2)
plt.title(f'学习率={lr}, 批量大小={bs}\n测试误差: {error_str} {size_tag}',
color=color, fontsize=10)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 显示最佳超参数组合,同样优化显示格式
best_lr, best_bs, best_error, _ = min(results, key=lambda x: x[2])
# 格式化最佳误差显示
if best_error > 1000:
best_error_str = f"{best_error:.2e}"
best_error_note = "(数值很大,建议检查模型)"
elif best_error > 100:
best_error_str = f"{best_error:.1f}"
best_error_note = "(数值较大)"
else:
best_error_str = f"{best_error:.2f}"
best_error_note = ""
print(f"\n 最佳超参数组合: 学习率={best_lr}, 批量大小={best_bs}")
print(f" 对应的测试误差: {best_error_str} {best_error_note}")
# 添加误差分析
print(f"\n 误差分析:")
all_errors = [result[2] for result in results]
print(f" 最小误差: {min(all_errors):.2e}")
print(f" 最大误差: {max(all_errors):.2e}")
print(f" 平均误差: {np.mean(all_errors):.2e}")
print(f" 误差标准差: {np.std(all_errors):.2e}")
# 显示所有结果的表格
print(f"\n 所有超参数组合结果:")
print(" LR Batch Test Error")
print(" --- ----- ----------")
for lr, bs, error, _ in sorted(results, key=lambda x: x[2]):
if error > 1000:
error_display = f"{error:.2e}"
elif error > 100:
error_display = f"{error:.1f}"
else:
error_display = f"{error:.2f}"
print(f" {lr:<6} {bs:<7} {error_display}")
print("生成超参数调优综合图...")
hyperparameter_tuning_demo2()输出结果:
最佳超参数组合: 学习率=0.01, 批量大小=20 对应的测试误差: 2.21 误差分析: 最小误差: 2.21e+00 最大误差: inf 平均误差: inf 误差标准差: nan 所有超参数组合结果: LR Batch Test Error --- ----- ---------- 0.01 20 2.21 0.01 50 2.24 0.001 5 2.26 0.001 20 2.27 0.001 50 2.35 0.01 5 3.70 0.1 50 1.64e+96 0.1 20 2.30e+188 0.1 5 inf
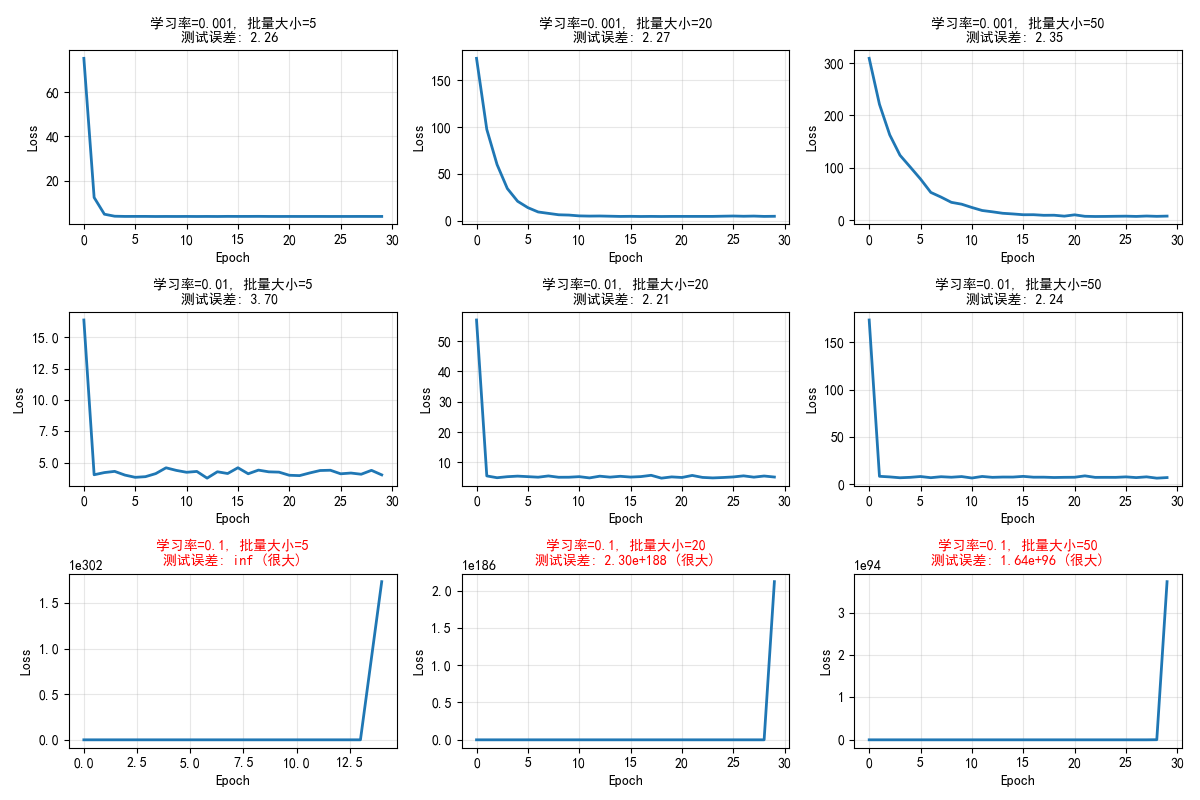
- 图片内容:
- 3x3网格显示不同学习率和批量大小组合下的训练过程
- 图片意义:
- 实际应用中需要同时调整多个超参数
- 网格搜索是常用的超参数调优方法
- 达到的效果:
- 直观比较不同超参数组合的性能
- 找到在测试集上表现最佳的超参数组合
- 理解超参数之间的相互作用
6. 示例总结
- 学习率:控制参数更新步长,影响收敛速度和稳定性
- 批量大小:平衡训练速度和稳定性,影响泛化能力
- 模型复杂度:控制拟合能力,防止欠拟合和过拟合
- 迭代次数:平衡训练时间和模型性能
七、总结
超参数是模型的预设,它们不直接从数据中学到,但决定了模型的学习行为。对大模型来说超参数调优是成功的关键,影响训练速度、性能和资源使用。如果我们是刚接触的初学者可以先从默认值开始,逐步实验调整,使用工具(如示例中的网格搜索)自动化过程。
超参数是机器学习模型在训练前设定的配置参数,它们控制着学习过程的各个方面,包括学习速度、模型复杂度、训练稳定性等,对最终模型性能有决定性影响,通过关联记忆将模型参数比喻为学生学到的知识,将超参数比喻为老师的教学方法和课程安排,只有两者配合才能培养出优秀的学生,才能训练出优秀的模型!
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
评论
登录后参与评论
推荐阅读
目录

