【背包问题】二维费用的背包问题

用户11719958

发布于 2025-12-30 14:58:24

1540

二维费用的背包问题详解

前面讲到的01背包中，对物品的限定条件只有一个体积，而在二维费用的背包问题中，相当于增加了一个限定条件，比如：

【问题描述】

输入：
- 物品数量 N，每个物品有重量 wi、体积 vi 和价值 vali。
- 背包最大承重 W，最大体积 V。
- 目标：选择物品装入背包，使得总重量 ≤ W，总体积 ≤ V，且总价值最大。

加了一个限定条件重量，那么状态表示也需加上一维。二维费用的背包问题时01背包问题的一个延申，状态表示和状态转移方程的分析与01背包类似。

状态表示是dp[i][j][k]，表示前i个物品，在重量限制j和体积限制k下的最大价值。

状态转移方程就是：dp[i][j][k] = max([i-1]dp[j][k], dp[i][j - w[i]][k - v[i]] + val[i]),推理过程与01背包类似。

总结：

常规的0-1背包问题可以用动态规划来解决，状态通常是dp[i][j]表示前i个物品，在容量j下的最大价值。对于二维费用的情况，可能需要扩展状态到两个维度。比如，状态可能是dp[i][j][k]，表示前i个物品，在重量限制j和体积限制k下的最大价值。但这样的话，状态空间会变得很大，尤其是当j和k都较大的时候，时间和空间复杂度可能很高。不过，可能可以通过优化来减少空间的使用，比如使用滚动数组。

空间优化：

在常规的0-1背包问题中，我们可以将二维的dp优化为一维数组，通过逆序遍历容量来避免覆盖之前的状态。那么在二维费用的情况下，使用二维的dp数组，而不是三维的。例如，状态dp[j][k]表示在重量j和体积k的限制下能获得的最大价值。这样的话，每次处理一个物品时，需要从后往前更新这两个维度，以避免重复选择同一物品。这可能需要双重循环，遍历重量和体积的容量。

1. 状态定义

定义二维数组 dp[j][k]，表示背包在承重 j 和体积 k 的限制下能获得的最大价值。
最终目标：求解 dp[W][V]。

2. 状态转移方程

对每个物品i，逆序更新所有可能的重量和体积组合：

dp[j][k]=max⁡(dp[j][k], dp[j−wi][k−vi]+vali)

条件：j≥wi 且 k≥vi

3. 初始化

dp[0][0]=0（空背包价值为0）。
其他位置初始化为0，表示未装入任何物品时的初始状态。

4. 遍历顺序

外层循环：遍历每个物品 i。
内层双循环：
- 重量 j 从 W 逆序递减至 wi。
- 体积 k 从 V 逆序递减至 vi。确保每个物品仅被选择一次。
- 5. 时间复杂度
- O(N×W×V)，适用于 W 和 VV均较小的情况（如 W,V≤10^3）。

例题

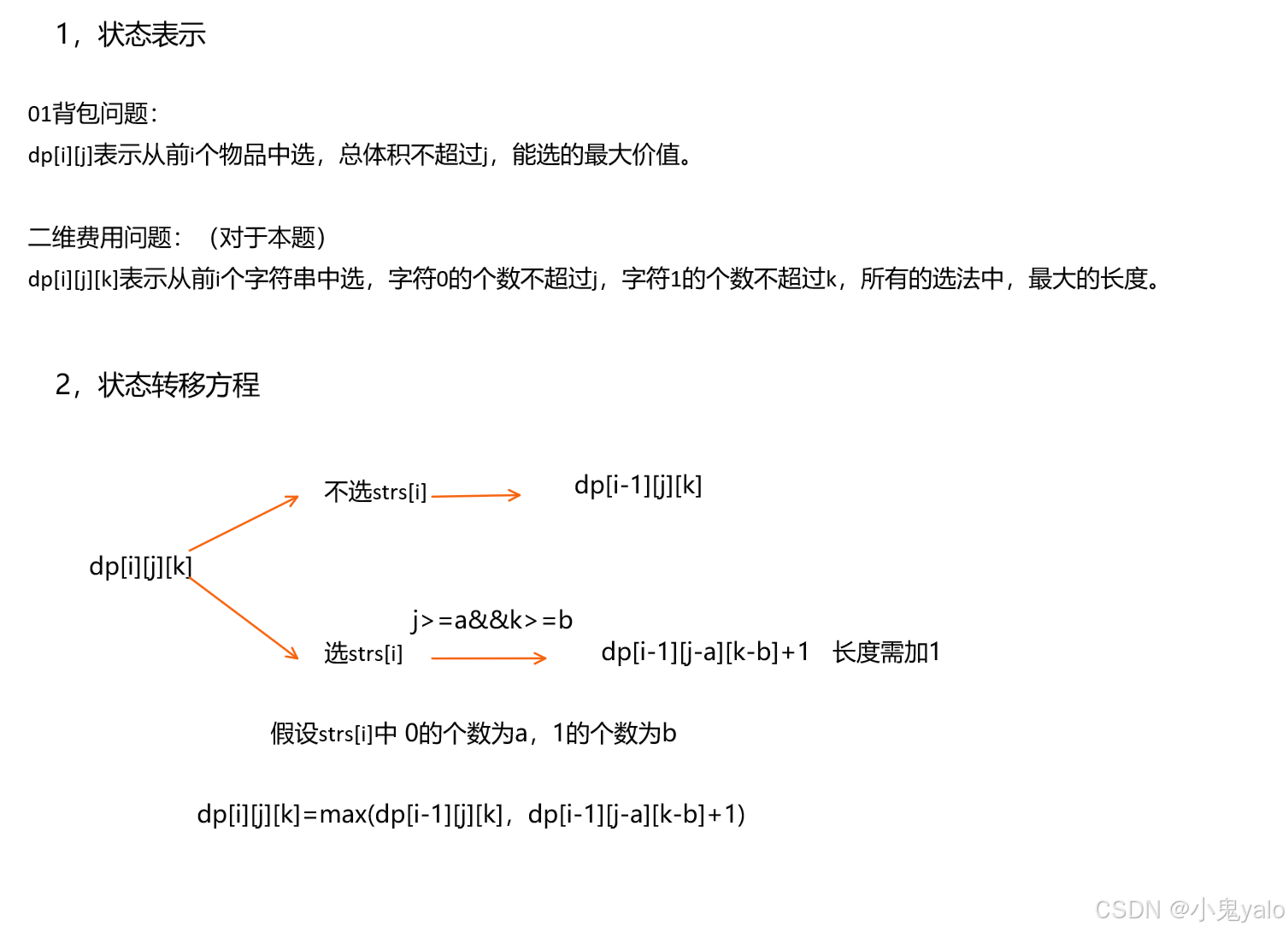
1，一和零

本题链接：474. 一和零 - 力扣（LeetCode）

思路：

从strs数组中选取子集，有两个限定条件m和n。相当于从背包中选取元素，有两个限定条件。

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int len=strs.size();

        vector<vector<vector<int>>> dp(len+1,vector<vector<int>>(m+1,vector<int>(n+1)));

        for(int i=1;i<=len;i++)
        {
            int a=0,b=0;
            for(auto& ch:strs[i-1])
            if(ch=='0') a++;
            else b++;

            for(int j=0;j<=m;j++)
            for(int k=0;k<=n;k++)
            {
                dp[i][j][k]=dp[i-1][j][k];
                if(j>=a&&k>=b)
                dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-a][k-b]+1);
            }
        }
        return dp[len][m][n];
    }
};

空间优化后的代码

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int len=strs.size();

       vector<vector<int>> dp(m+1,vector<int>(n+1));

        for(int i=1;i<=len;i++)
        {
            int a=0,b=0;
            for(auto& ch:strs[i-1])
            if(ch=='0') a++;
            else b++;

            for(int j=m;j>=a;j--)
            for(int k=n;k>=b;k--)
                dp[j][k]=max(dp[j][k],dp[j-a][k-b]+1);
            
        }
        return dp[m][n];
    }
};

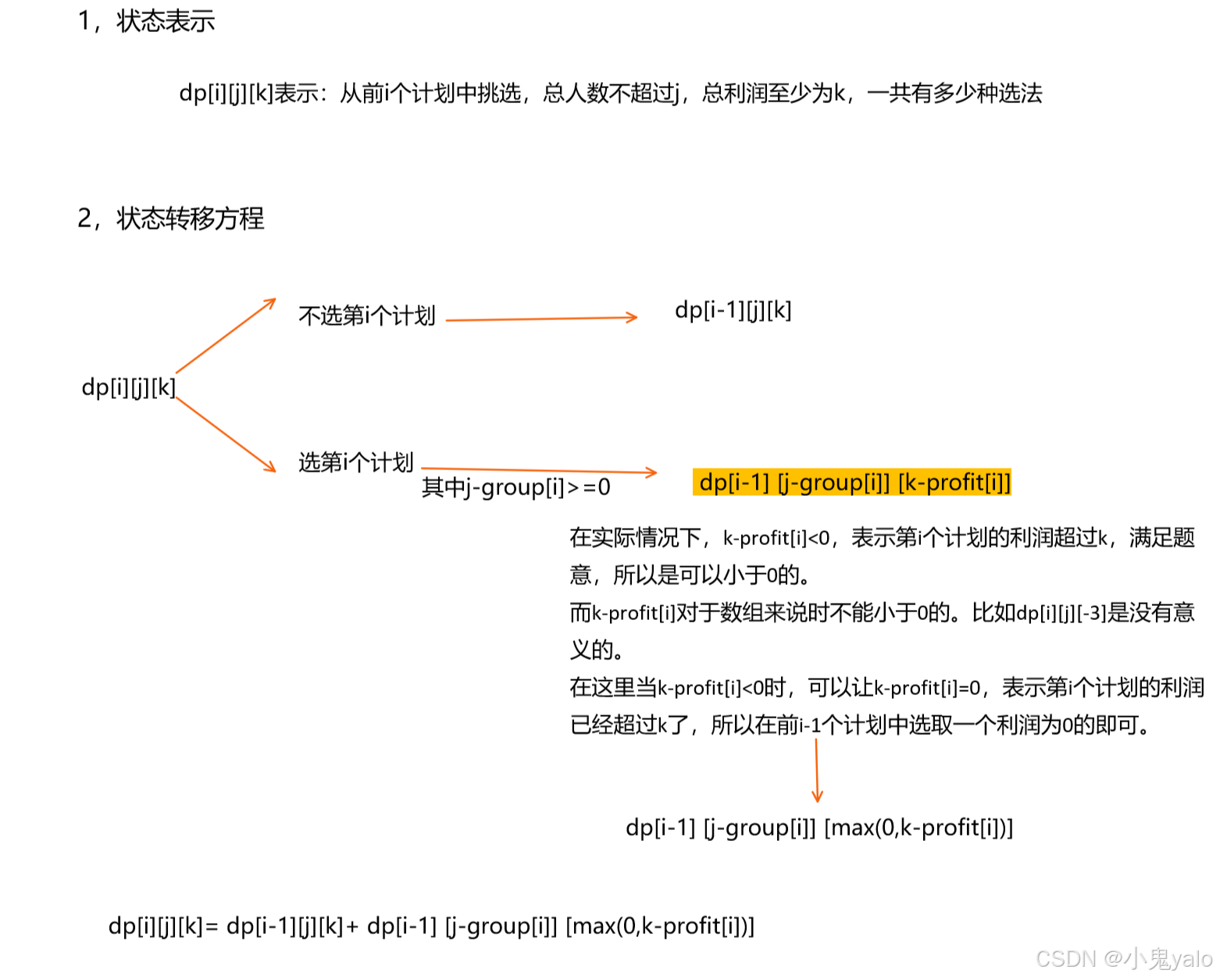
2，盈利计划

本题链接：879. 盈利计划 - 力扣（LeetCode）

思路：

class Solution {
public:
    int profitableSchemes(int n, int m, vector<int>& g, vector<int>& p) {
        int len=g.size();
        const int MOD=1e9+7;

        vector<vector<vector<int>>> dp(len+1,vector<vector<int>>(n+1,vector<int>(m+1)));

        for(int j=0;j<=n;j++)
        dp[0][j][0]=1;

        for(int i=1;i<=len;i++)
        for(int  j=0;j<=n;j++)
        for(int k=0;k<=m;k++)
        {
            dp[i][j][k]=dp[i-1][j][k];
            if(j>=g[i-1])
            dp[i][j][k]+=dp[i-1][j-g[i-1]][max(0,k-p[i-1])];
            dp[i][j][k]%=MOD;
          
        }
        return dp[len][n][m];
    }
};

空间优化后的代码

class Solution {
public:
    int profitableSchemes(int n, int m, vector<int>& g, vector<int>& p) {
        int len=g.size();
        const int MOD=1e9+7;

       vector<vector<int>> dp(n+1,vector<int>(m+1));

        for(int j=0;j<=n;j++)
        dp[j][0]=1;

        for(int i=1;i<=len;i++)
        for(int j=n;j>=g[i-1];j--)
        for(int k=m;k>=0;k--)
        {
            dp[j][k]+=dp[j-g[i-1]][max(0,k-p[i-1])];
            dp[j][k]%=MOD;
          
        }
        return dp[n][m];
    }
};

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-12-30，如有侵权请联系 cloudcommunity@tencent.com 删除

遍历