【C语言】数据在内存中的存储（超详解）

一、整数在内存中的存储

1.存储形式

整型数据在内存中存储的是二进制的补码形式,这是计算机中表示整数的标准方式。

那么，什么是补码呢？

2.原码、反码和补码

整数的的2进制表示形式有三种，分别是原码、反码和补码

对于有符号的整数来说：

有符号位和数值位两部分。在二进制中，最高一位是符号位，其余都是数值位。在符号位中，0表示正数，1表示负数 正整数的原码、反码和补码都相同 而负整数的则各不相同，有对应的转换规则

对于无符号的整数来说： 全是数值位，无符号位

3.原码

直接将数值按照正负数形式翻译成二进制，最高一位是符号位，其余都是数值位（有符号的整数） 且对于 int 类型来说，占 4 个字节，32 个 bit 位

这里我们拿 37 和 - 37 一正一负举例 37 的原码：( 标记的是符号位，下同） 在符号位中，0表示正数，1表示负数，故37第一位是0

0000 0000 0000 0000 0000 0000 0010 0101

- 37 的原码：

1000 0000 0000 0000 0000 0000 0010 0101

4.反码

对于正数，原码、反码和补码都相同，故不变 但对于负数，原码的符号位不变，其他位按位取反（1变为0，0变为1）

37 的反码：

0000 0000 0000 0000 0000 0000 0010 0101

-37 的反码：原码按位取反

1111 1111 1111 1111 1111 1111 1101 1010

5.补码

对于正数，原码、反码和补码都相同，故不变 但对于负数，反码+1得到补码（注意进位）

37 的补码：

0000 0000 0000 0000 0000 0000 0010 0101

-37 的补码：反码+1

1111 1111 1111 1111 1111 1111 1101 1011

6.补码的优势

前面我们也提到： 整型数据在内存中存储的是二进制的补码形式

但为什么呢？

原因是： 统一处理：可以将符号位和数值域统一处理 运算简化：加法和减法可以统一处理（CPU只有加法器） 硬件优势：补码与原码相互转换运算过程相同，不需要额外硬件电路

二、大小端字节序和字节序判断

1.什么是大小端？

整型数据在内存中以二进制补码形式存储，超过1字节的数据存在字节序问题 大端字节序和小端字节序描述的是多字节数据在内存中以字节为单位的存储顺序

以 int a = 0x 11 22 33 44 ;为例，如图：

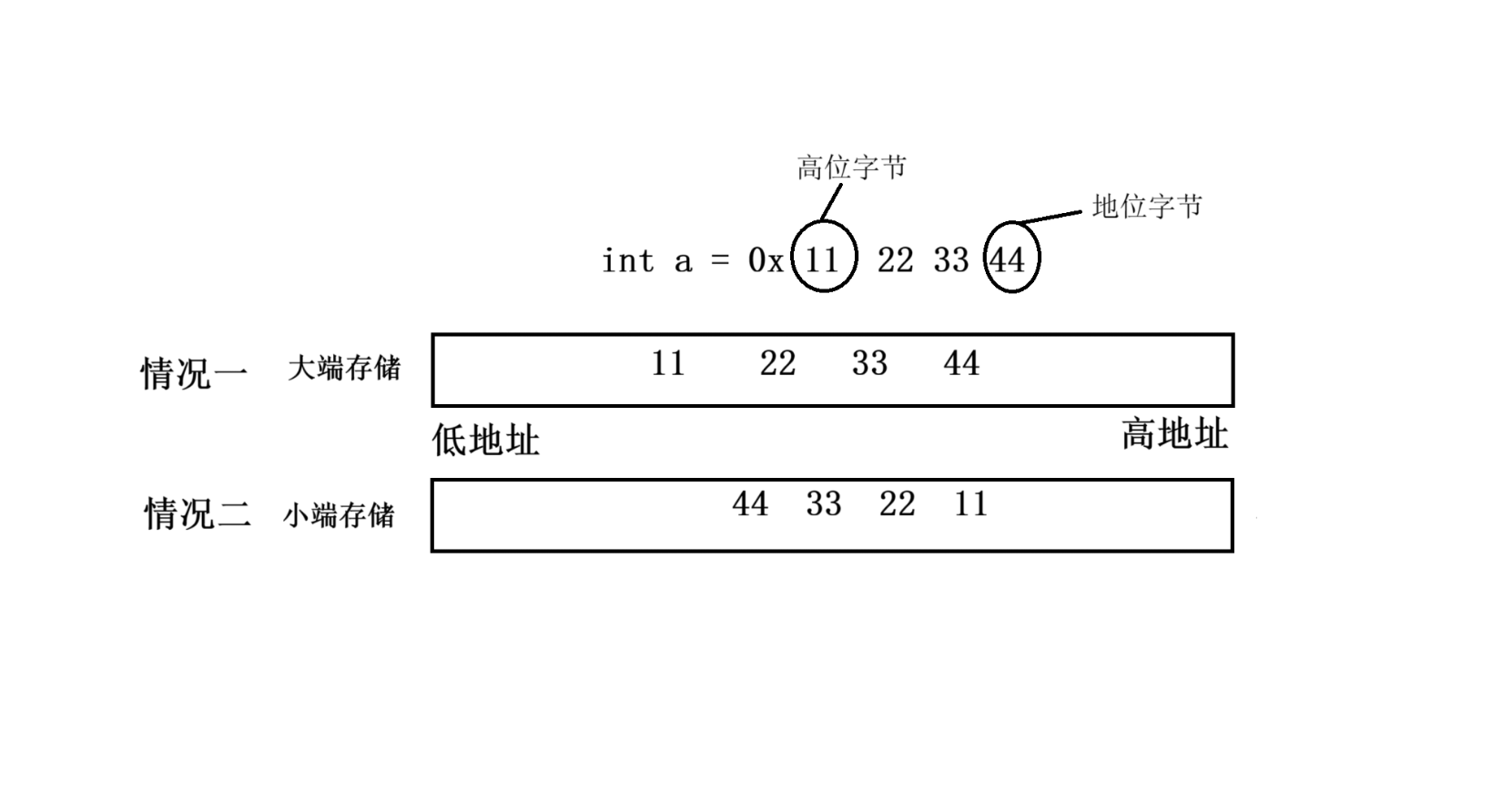
在这里插入图片描述

有上下两种情况存储，大端和小端

大端字节序:(上） 数据的高位字节存储在低地址处，低位字节存储在高地址处 小端字节序:（下） 数据的低位字节存储在低地址处，高位字节存储在高地址处

2.为什么要有大小端？

存储单元限制: 计算机以字节(8bit)为最小寻址单位 数据类型差异：C语言存在16bit(short)、32bit(int/long)等跨字节类型 硬件差异：处理器寄存器宽度可能大于1字节（如16/32位处理器） 总的来说： 大小端存储模式是为了解决将多个字节安排的问题 无论采用哪种字节序，必须保证存取的顺序一致性

3.判断大小端模式

由于int a = 1 ;中的 a 储存的是0x 00 00 00 01 故可以将 a 内存中第一个字节取出来，判断是 1 还是 0 是 1 就是小端模式，否则是大端模式

代码演示：（这里我用的是VS2022）

#include <stdio.h>

int main() 
{
	int a = 1;
	////0x 00 00 00 01
	int ret = *(char*)&a;
	//强制类型转换将 4 字节的int型转为 1 字节的 char 型
	//便于将 a 内存中第一个字节取出来
	if (ret == 1)
		printf("小端模式\n\n");
	else
		printf("大端模式\n\n");

	return 0;
}

运行结果：

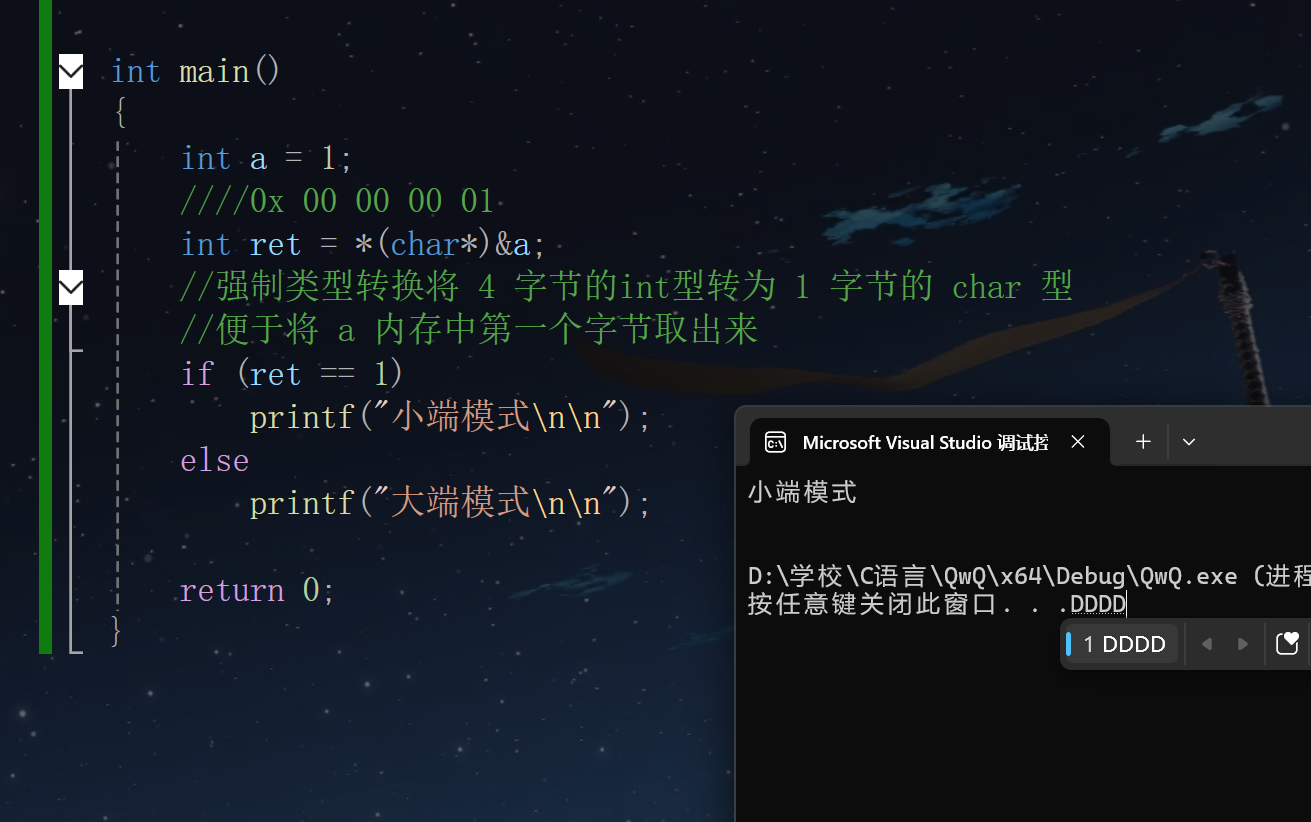
在这里插入图片描述

可以看到，在VS2022上，是小端存储模式 编译器不同，结果也不同，大家也可以自己去尝试哦

三、浮点数在内存中的存储

1.观察现象

这里有一段代码，大家可以猜一猜运行结果 结果你绝对想不到

代码演示：

#include <stdio.h>

int main()
{
	int g = 9;
	float* p = (float*)&g;

	printf("%d\n\n", g);
	printf("%f\n\n", *p);

	*p = 9.0;

	printf("%d\n\n", g);
	printf("%f\n\n", *p);

	return 0;
}

运行结果：

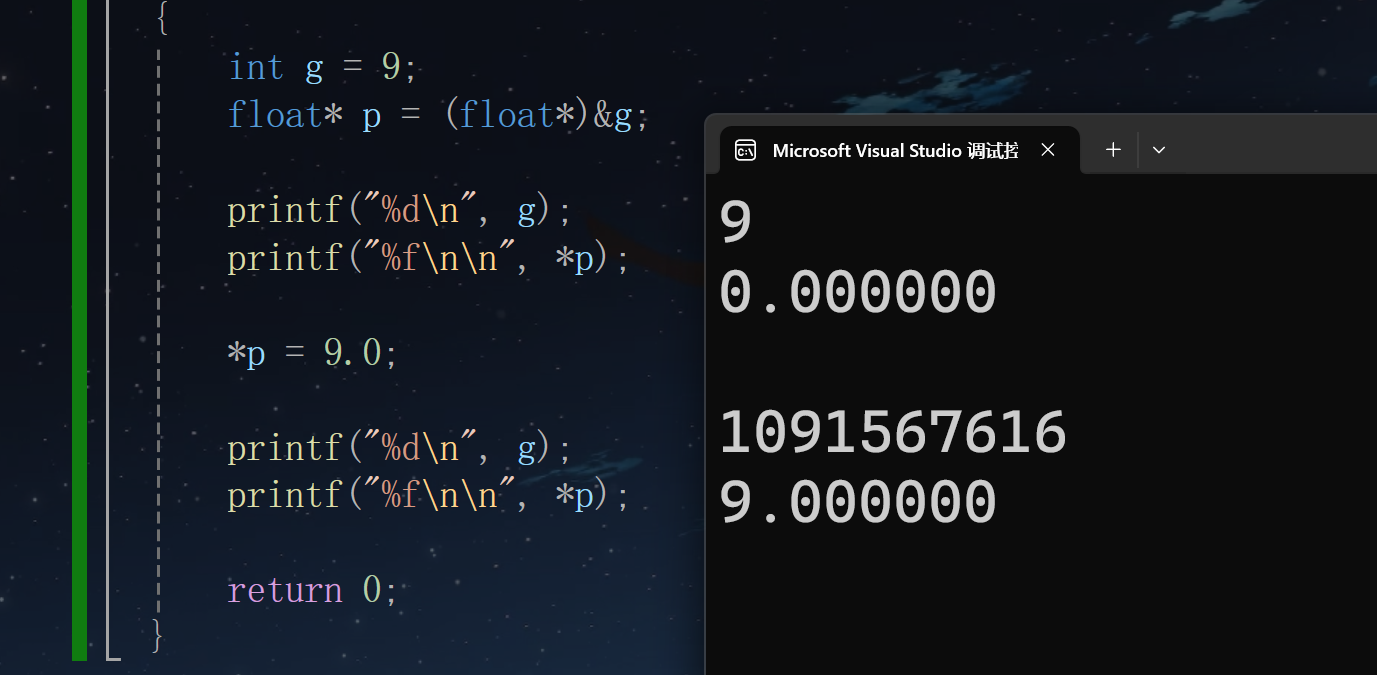
在这里插入图片描述

结果是不是想不到，为什么第2个是0，而第三个这么大呢？ 听我一一道来：

2.浮点数内存存储

根据国际标准IEEE(电气和电子工程协会)754，任意一个浮点数V可以表现为下面的形式： V=(-1)^s * M * 2^E

• (-1)^S表示符号位，当S=0时，V为正数，当S=1时，V为负数
• M表示有效数字，M大于等于1，小于2
• 2^E表示指数位

例如： 十进制数 5.5 转换成二进制数是 101.1 （ 5.5=1 * 2^2 + 1 * 2^0 + 1 * 2^(-1) )

故 101.1 = (-1)^0 * 1.011 * 2^ 2(二进制计算） 故S = 0 , M = 1.011 , E = 2

所以浮点数的存储，其实就是存的和S，M，E相关的值

• 对于32位浮点数（float类型） S占1bit 位 ， E占8bit位 ， M占23bit位 如图：

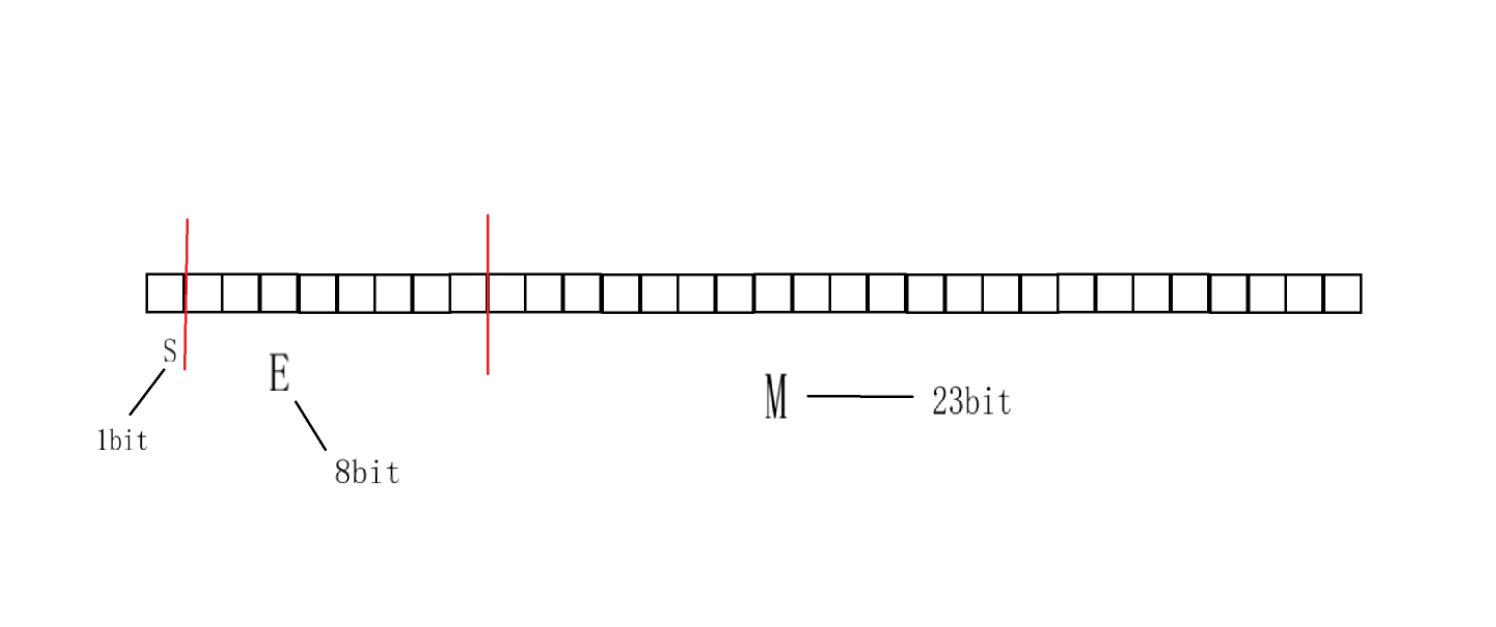
在这里插入图片描述

• 对于64位浮点数（double类型） S占1bit 位 ， E占11bit位 ， M占52bit位 如图：

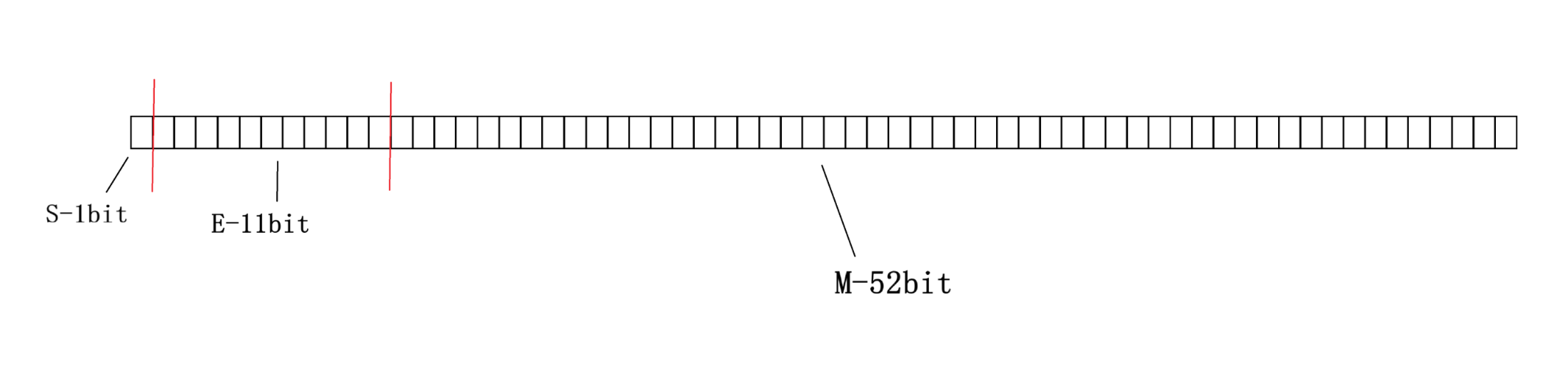
在这里插入图片描述

3.S、E、M

• S

当S=0时，V为正数，当S=1时，V为负数

• M

由于 1 <= M <2 ,故 M = 1. xxxxxx，在内存M中只存放小数点后的xxxxxx

• E

E为无符号整数 故对于8bit位的E取值范围为[ 0 , 255 ]( 111 1111 ) 对于11bit位的E取值范围为[ 0 , 2047 ]( 111 1111 1111 ) 但为了E可以存储负数，E在存入内存的真实值要加一个中间数 8 bit位的E + 127 ; 11 bit位的E + 1023 例如： 2^10 的E是10，保存成32位浮点数时，E要加127 以10001001（137）保存

4.特殊情况

• 当E全为0时

此时E的真实值是 - 127，且有效数字M的第一位不再是 1 ，改为0。 V = +/- 0.xxxxxx * 2^(-127) 此时V无限趋近于0 故E为全0是为了表示 0，以及无限趋近于0的数

• 当E全为1时

此时E的真实值是 128 V = +/- 1.xxxxxx * 2^128 此时V无限趋近于正负无穷 故E为全1是为了表示无穷小或无穷大的数

5.回到例题

现在，我们学完了浮点数在内存中的存储 也可以看懂之前的例题了

#include <stdio.h>

int main()
{
	int g = 9;
	float* p = (float*)&g;

	printf("%d\n", g);//9
	printf("%f\n\n", *p);//0.000000

	*p = 9.0;

	printf("%d\n", g);//1091567616
	printf("%f\n\n", *p);//9.000000

	return 0;
}

1 和 4 没什么好说的，之前的学习中已经给大家讲过了，主要是 2 和 3 的问题

• 第2题

首先，取出g的地址再强制类型转换给指针p,再以浮点数形式打印

这里文字解释不清，我用图解来讲解吧 大家在写这种题目时也要多画图哦

在这里插入图片描述

所以，第2个答案是0.00000000

• 第3题

首先，取出 g 的地址再强制类型转换给指针 p ，再通过解引用把 g 的值改为 9.0 (浮点数），最后以整型形式打印

这里依旧图解：

在这里插入图片描述

想必大家通过我的图解已经把题目原理搞清楚了 以后大家在做这种题目时，一定要多画草图，把大概框架画出来 分析数据在内存中怎放置，分析怎样读取内存的数据 做完这些后，题目也就迎刃而解了

结语

本期资料来自于：

https://legacy.cplusplus.com/

OK，本期（数据在内存中的存储）详解到这里就结束了 若内容对大家有所帮助,可以收藏慢慢看,感谢大家支持 本文有若有不足之处，希望各位兄弟们能给出宝贵的意见。谢谢大家！！！ 新人，本期制作不易希望各位兄弟们能动动小手，三连走一走！！！ 支持一下（三连必回QwQ）