构建AI智能体:大模型涌现能力的解构分析:从量变到质变的神秘跃迁
原创构建AI智能体:大模型涌现能力的解构分析:从量变到质变的神秘跃迁
原创
未闻花名
发布于 2026-01-12 07:48:52
发布于 2026-01-12 07:48:52
一、前言
涌现能力是指当系统复杂度达到某个阈值时,整体表现出其组成部分所不具备的新特性,它描述了当模型规模达到某个临界点时,突然出现的新能力和行为模式。这种现象不能简单地通过分析模型的组成部分来预测,而是整体系统在复杂度达到阈值时产生的质变。就像单个水分子没有湿润的特性,但大量水分子聚集时却涌现出液体的各种特性,单个神经元不会思考,但神经网络产生了意识,诸如此类简单规则可以涌现出复杂的生命行为,大语言模型在参数规模突破百亿级别后,开始展现出令人惊讶的智能行为。
这种能力的涌现不是线性的渐进过程,而是类似物理学中的相变现象。当模型规模较小时,其能力主要表现为模式匹配和记忆检索;一旦跨越某个规模阈值,模型突然获得了推理、创造、理解等高级认知能力。这种跃迁不仅改变了我们对人工智能的理解,也为通用人工智能的发展提供了新的路径。

二、涌现能力的体现
通常小模型完成简单模式的匹配,例如我们问它2+2等于多少时,它会返回记忆中的答案4,或者问它“如果我有3个苹果,吃了1个,还剩几个?”,它也会简单的算术,告诉我们结果是2,甚至还可以告诉我们它的计算过程。
而到了大模型,则表现出强大的逻辑推理能力,当我们问它“小明比小红高,小红比小刚高,谁最矮?”,大模型会输出一步步的推理过程:“小明 > 小红;小红 > 小刚 ;因此:小明 > 小红 > 小刚;所以小刚最矮”。
当模型参数规模达到百亿级别时,逻辑推理能力出现了质的飞跃。这种能力并非通过显式的逻辑规则编程获得,而是模型从海量文本数据中自行抽象出的推理模式。最初表现为简单的三段论推理,如从"A大于B,B大于C"推导出"A大于C",随后逐渐发展为处理复杂的多步骤推理问题。
这种推理能力的涌现具有明显的层次性。在较低规模时,模型只能处理明确的、直接的逻辑关系;随着规模增长,模型开始能够理解隐含的前提条件,处理不确定信息,甚至进行反事实推理。例如,当被问及"如果拿破仑赢得了滑铁卢战役,欧洲历史会如何发展"时,具备涌现能力的模型能够构建合理的替代历史场景,而不是简单地回复"这没有发生"。
三、涌现能力的理论说明
1. 尺度定律
1.1 核心思想
尺度定律的核心思想是:模型性能与训练计算量、模型参数量、训练数据量之间存在幂律关系。这意味着当我们将资源投入增加一个数量级时,模型性能会以可预测的方式提升特定幅度。这种关系在多个数量级范围内保持稳定,为人工智能的发展提供了可靠的预测框架。
1.2 尺寸定律维度
尺度定律主要围绕三个核心维度展开:
- 计算尺度:训练模型所需的总计算浮点运算次数(FLOPs)。这是最基础的尺度维度,直接决定了模型能够从数据中提取多少信息。
- 参数尺度:模型的参数量。更多的参数意味着模型具有更强的表示能力,可以捕捉更复杂的数据模式。
- 数据尺度:训练数据的规模和质量。足够的数据是模型学习的基础,数据多样性决定了模型能力的广度。
这三个维度之间存在复杂的相互作用,但它们各自对最终性能的贡献都遵循着明确的数学规律。
1.3 尺度定律的数学表达
1.3.1 基本数学形式
尺度定律可以用简洁的幂律公式表示:
L(C) ≈ (C₀/C)^α
其中:
- L(C) 是使用计算量C训练得到的损失值
- C₀ 和 α 是通过实证确定的常数
- α 通常取值在0.05到0.1之间
这个公式表明,损失值随着计算量的增加而按照幂律关系下降。在双对数坐标图上,这种关系表现为一条直线,使得预测变得直观而准确。
1.3.2 多维度扩展公式
更完整的尺度定律考虑了三者的共同作用:
L(N,D) = (N₀/N)^α_N + (D₀/D)^α_D + L∞
这里:
- N 是模型参数量
- D 是训练数据量
- L∞ 是 irreducible loss,表示任务的本质难度
- 其他参数通过大规模实验拟合确定
这个扩展公式揭示了不同资源之间的最优分配策略,为实际训练提供了理论指导。
1.4 示例可视化
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def scaling_laws_visualization():
"""尺度定律可视化:性能随规模增长的变化"""
# 模拟不同规模下的模型性能
model_sizes = [1e6, 1e7, 1e8, 1e9, 1e10, 1e11, 1e12] # 参数量
performance = [0.1, 0.2, 0.3, 0.4, 0.6, 0.8, 0.95] # 性能指标
# 临界点位置(涌现开始)
emergence_point = 1e10 # 约100亿参数
plt.figure(figsize=(10, 6))
plt.tight_layout()
# 绘制性能曲线
plt.semilogx(model_sizes, performance, 'b-o', linewidth=3, markersize=8, label='模型性能')
# 标记涌现临界点
plt.axvline(x=emergence_point, color='red', linestyle='--', linewidth=2,
label=f'涌现临界点 ({emergence_point:.0e} 参数)')
# 标注不同阶段
plt.annotate('简单模式匹配', xy=(1e7, 0.15), xytext=(1e6, 0.05),
arrowprops=dict(arrowstyle='->', color='gray'), fontsize=12)
plt.annotate('基础推理能力', xy=(1e10, 0.45), xytext=(1e9, 0.3),
arrowprops=dict(arrowstyle='->', color='gray'), fontsize=12)
plt.annotate('复杂推理涌现', xy=(1e11, 0.75), xytext=(1e10, 0.6),
arrowprops=dict(arrowstyle='->', color='red'), fontsize=12)
plt.xlabel('模型参数量 (log scale)')
plt.ylabel('综合性能指标')
plt.title('大模型涌现能力的尺度定律')
plt.legend()
plt.grid(True, alpha=0.3)
plt.subplots_adjust(left=0.07, right=0.97, top=0.95, bottom=0.1)
plt.show()
# 运行可视化
scaling_laws_visualization()输出结果:
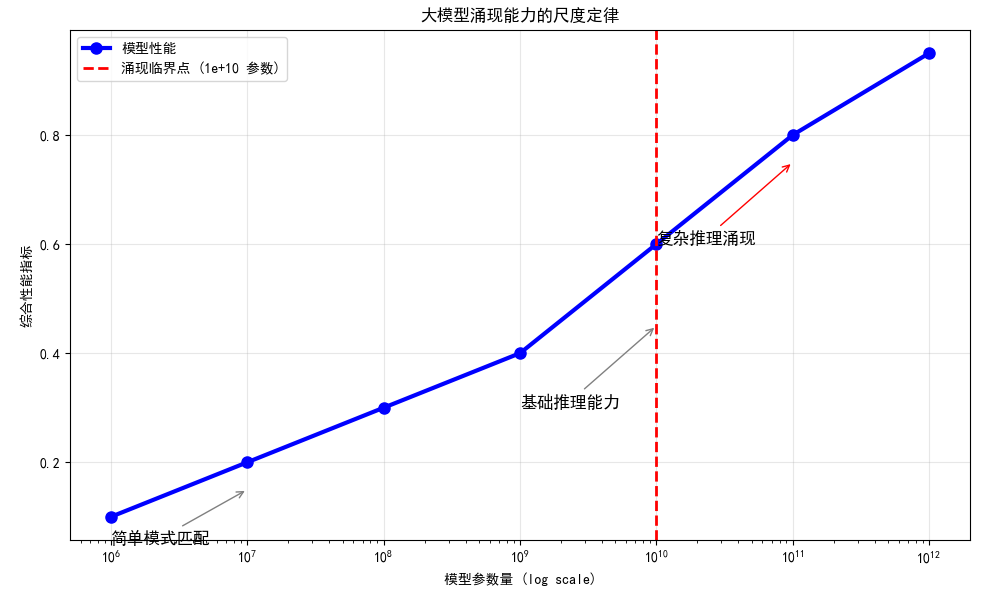
想象我们养一盆植物:
- 小苗期(1000万参数):只能长叶子(简单记忆)
- 生长期(10亿参数):开始长枝条(基础推理)
- 开花期(1000亿参数):突然开出美丽的花朵(复杂推理涌现)
图例分析:
- X轴(横坐标):模型的大小,就像植物的高度。从100万到1万亿参数,数字越大模型越"聪明"
- Y轴(纵坐标):模型的聪明程度,0.1是很笨,0.95是非常聪明
- 红色虚线:这是一个魔法门槛,跨过这条线(约1000亿参数),模型突然变得特别聪明
- 三个标注:
- "简单模式匹配":像鹦鹉学舌,只会重复
- "基础推理能力":开始理解简单问题
- "复杂推理涌现":突然会解决难题了!
通俗的讲,就像小孩学数学:
- 3岁:只会数1,2,3(记忆)
- 6岁:会算1+1=2(简单推理)
- 12岁:突然会解方程了(涌现)
2. 相变理论
2.1 核心思想
相变理论最初来源于物理学,描述了物质在外部条件(如温度、压力)变化时,从一种状态突然转变为另一种状态的现象。这种转变不是渐进的,而是在临界点发生的突然质变。最经典的例子包括:
- 水的三态变化:当温度达到0°C时,水从液态突然转变为固态(冰);当温度达到100°C时,又从液态突然转变为气态(水蒸气)。这些转变点就是相变临界点。
- 磁铁的有序-无序转变:铁磁材料在居里温度以上会突然失去磁性,从有序的铁磁相转变为无序的顺磁相。
- 超导转变:某些材料在临界温度以下突然出现零电阻和完全抗磁性。
这些物理相变的共同特征是:在临界点附近,系统的微观组元(分子、原子、自旋)通过集体协作,涌现出全新的宏观特性,这些特性无法从单个组元的行为中预测。
2.2 大模型中的相变体现
2.2.1 语言理解能力的相变
在大模型的训练过程中,语言理解能力呈现出清晰的相变特征:
- 词汇理解的相变:当模型规模较小时,它只能进行表面的词汇匹配。达到临界规模后,突然能够理解词汇的语义关系和上下文含义。
- 语法结构的相变:从简单的语法模式识别突然转变为深层语法结构理解,能够处理复杂的长距离依赖关系。
- 语义推理的相变:在某个规模阈值,模型突然能够进行逻辑推理和常识推理,而不仅仅是文本模式匹配。
这些相变不是平滑过渡,而是在相对狭窄的参数范围内突然发生。例如,某个模型可能在750亿参数时还无法可靠处理复杂推理,但在800亿参数时突然具备了这种能力。
2.2.2 推理能力的层次化相变
推理能力的涌现呈现出多层次相变特征:
- 基础逻辑相变:首先出现的是命题逻辑和简单推理能力,如从"A推出B,B推出C"推导出"A推出C"。
- 概率推理相变:随后出现处理不确定性和概率信息的能力,能够进行贝叶斯推理和风险评估。
- 反事实推理相变:最高层次是反事实推理能力,能够思考"如果情况不同,会发生什么"的假设性问题。
每个层次的相变都对应着不同的规模阈值,形成了能力涌现的阶梯式结构。
2.3 示例可视化
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class EmergencePhaseTransition:
"""涌现能力的相变理论分析"""
def __init__(self):
self.capabilities = {
'memorization': '记忆能力',
'pattern_matching': '模式匹配',
'simple_reasoning': '简单推理',
'complex_reasoning': '复杂推理',
'creativity': '创造性思维'
}
def analyze_phase_transition(self, model_size):
"""分析不同规模下的能力相变"""
if model_size < 1e7: # 1000万参数
return ['memorization']
elif model_size < 1e9: # 10亿参数
return ['memorization', 'pattern_matching']
elif model_size < 1e10: # 100亿参数
return ['memorization', 'pattern_matching', 'simple_reasoning']
elif model_size < 1e11: # 1000亿参数
return ['memorization', 'pattern_matching', 'simple_reasoning', 'complex_reasoning']
else: # 万亿参数
return ['memorization', 'pattern_matching', 'simple_reasoning', 'complex_reasoning', 'creativity']
def plot_capability_emergence(self):
"""绘制能力涌现图谱"""
sizes = [1e6, 1e7, 1e8, 1e9, 1e10, 1e11, 1e12]
capabilities_count = [len(self.analyze_phase_transition(size)) for size in sizes]
plt.figure(figsize=(14, 8))
# 绘制能力数量变化
plt.subplot(2, 2, 1)
plt.semilogx(sizes, capabilities_count, 'g-s', linewidth=3, markersize=8)
plt.xlabel('模型规模 (参数)')
plt.ylabel('能力数量')
plt.title('能力数量随规模增长')
plt.grid(True, alpha=0.3)
# 绘制能力热图
plt.subplot(2, 2, 2)
capability_matrix = []
for size in sizes:
capabilities = self.analyze_phase_transition(size)
row = [1 if cap in capabilities else 0 for cap in self.capabilities.keys()]
capability_matrix.append(row)
capability_matrix = np.array(capability_matrix)
plt.imshow(capability_matrix.T, cmap='YlGnBu', aspect='auto')
plt.yticks(range(len(self.capabilities)), [self.capabilities[cap] for cap in self.capabilities.keys()])
plt.xticks(range(len(sizes)), [f'{size:.0e}' for size in sizes], rotation=45)
plt.title('能力涌现热图')
plt.colorbar(label='能力存在性')
# 绘制相变边界
plt.subplot(2, 2, 3)
x = np.logspace(6, 12, 100)
y_memory = np.ones_like(x)
y_pattern = np.where(x >= 1e7, 1, 0)
y_simple = np.where(x >= 1e9, 1, 0)
y_complex = np.where(x >= 1e10, 1, 0)
y_creative = np.where(x >= 1e11, 1, 0)
plt.semilogx(x, y_memory, label='记忆能力', linewidth=2)
plt.semilogx(x, y_pattern, label='模式匹配', linewidth=2)
plt.semilogx(x, y_simple, label='简单推理', linewidth=2)
plt.semilogx(x, y_complex, label='复杂推理', linewidth=2)
plt.semilogx(x, y_creative, label='创造性', linewidth=2)
plt.xlabel('模型规模')
plt.ylabel('能力激活')
plt.title('能力相变边界')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 运行相变分析
phase_analysis = EmergencePhaseTransition()
phase_analysis.plot_capability_emergence()输出结果:
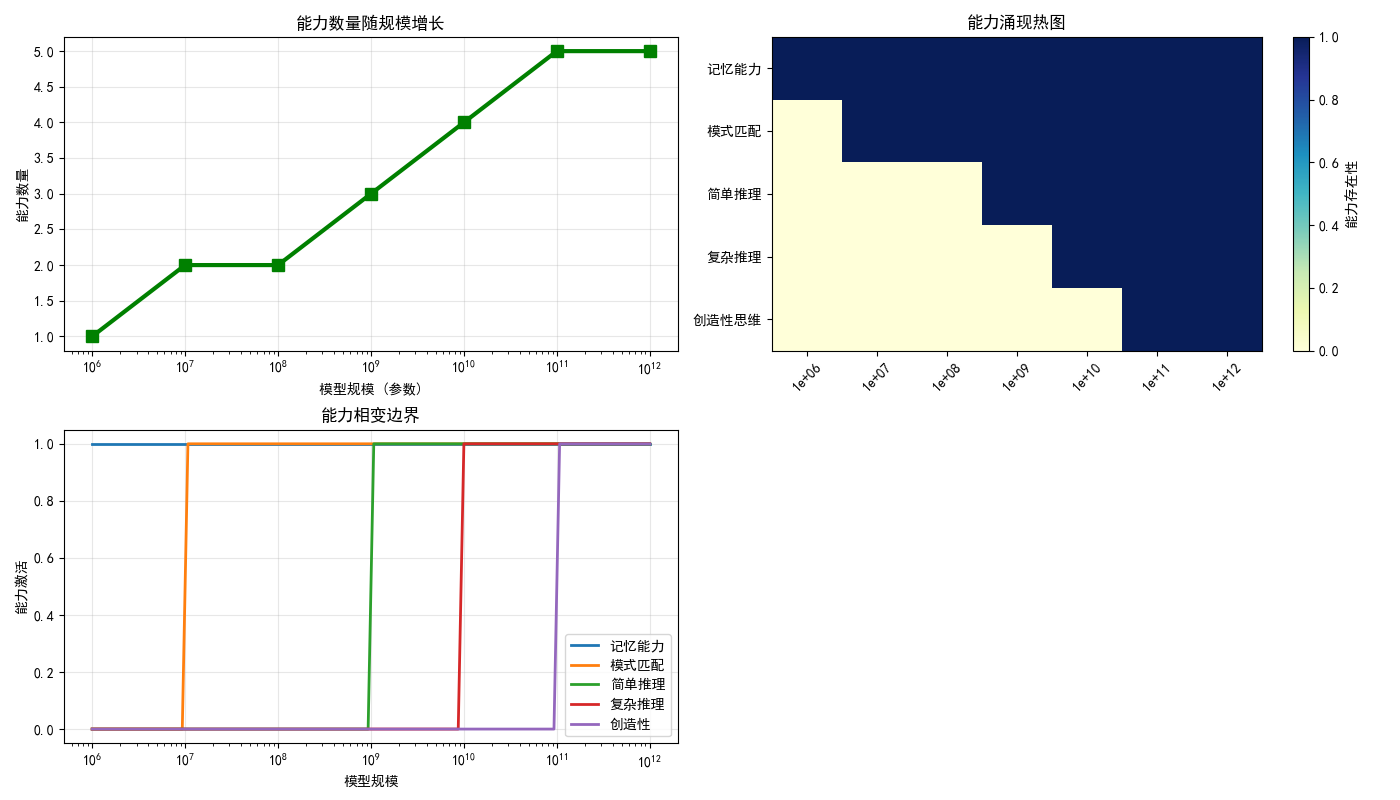
图例分析:
图一:能力数量随规模增长
- 参数规模越大所体现出的能力价值越大
图二:能力涌现热图
- Y轴(纵坐标):五种能力,从简单到复杂
- X轴(横坐标):模型大小,从左到右越来越大
- 颜色深浅:蓝色越深表示这个能力越强
- 观察规律:随着模型变大,蓝色方块从下往上"爬",解锁新能力
生活比喻,就像学开车:
- 小模型:只会踩油门刹车(记忆)
- 中模型:会转弯了(模式匹配)
- 大模型:会倒车入库了(推理)
- 超大模型:会漂移了(创造)
图三:能力相变边界
- X轴:还是模型大小
- Y轴:能力是否激活(0=没有,1=有)
- 五条线:每条线代表一种能力
- 关键观察:每条线都在某个点从0突然跳到1,这就是"相变"
生活比喻,就像烧开水:
- 50°C:没动静
- 80°C:还是没动静
- 100°C:突然沸腾!
模型能力也是这样,达到某个规模就"沸腾"了。
四、涌现能力的案例实践
1. 数学推理的涌现
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class MathematicalReasoningEmergence:
"""数学推理能力的涌现分析"""
def __init__(self):
self.problem_types = {
'arithmetic': '算术运算',
'algebra': '代数求解',
'geometry': '几何证明',
'probability': '概率计算',
'calculus': '微积分'
}
def test_reasoning_capability(self, model_size, problem_type):
"""测试不同规模模型的数学推理能力"""
# 模拟不同难度的问题
problems = {
'arithmetic': "计算: (15 × 24) ÷ 6 + 18",
'algebra': "解方程: 2x² - 5x + 3 = 0",
'geometry': "证明: 直角三角形斜边上的高是两条直角边在斜边上的投影的比例中项",
'probability': "从52张扑克牌中随机抽取5张,得到同花顺的概率是多少?",
'calculus': "求函数 f(x) = x³ - 3x² + 2x 在区间 [0, 3] 上的最大值和最小值"
}
# 不同规模模型的预期表现
performance_thresholds = {
'arithmetic': 1e7, # 1000万参数
'algebra': 1e9, # 10亿参数
'geometry': 5e10, # 500亿参数
'probability': 1e11, # 1000亿参数
'calculus': 5e11 # 5000亿参数
}
threshold = performance_thresholds.get(problem_type, float('inf'))
return model_size >= threshold
def analyze_math_emergence(self):
"""分析数学推理能力的涌现模式"""
model_sizes = [1e6, 1e7, 1e8, 1e9, 1e10, 1e11, 1e12]
plt.figure(figsize=(15, 10))
# 为每种问题类型绘制能力曲线
for i, (prob_type, prob_name) in enumerate(self.problem_types.items()):
capabilities = []
for size in model_sizes:
capable = self.test_reasoning_capability(size, prob_type)
capabilities.append(1 if capable else 0)
# 找到能力涌现点
emergence_point = None
for j, (size, capable) in enumerate(zip(model_sizes, capabilities)):
if capable and (j == 0 or not capabilities[j-1]):
emergence_point = size
break
plt.subplot(2, 3, i+1)
plt.semilogx(model_sizes, capabilities, 'o-', linewidth=3, markersize=8)
if emergence_point:
plt.axvline(x=emergence_point, color='red', linestyle='--', alpha=0.7)
plt.annotate(f'涌现点: {emergence_point:.0e}',
xy=(emergence_point, 0.5), xytext=(emergence_point*2, 0.7),
arrowprops=dict(arrowstyle='->', color='red'))
plt.title(f'{prob_name}能力涌现')
plt.xlabel('模型规模')
plt.ylabel('能力具备')
plt.yticks([0, 1], ['否', '是'])
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 打印分析结果
print("数学推理能力涌现分析:")
print("+" + "-"*50 + "+")
for prob_type, prob_name in self.problem_types.items():
min_size = min([size for size in model_sizes
if self.test_reasoning_capability(size, prob_type)], default=float('inf'))
print(f"| {prob_name:12} | 涌现规模: {min_size:>8.0e} 参数 |")
print("+" + "-"*50 + "+")
# 运行数学推理分析
math_analysis = MathematicalReasoningEmergence()
math_analysis.analyze_math_emergence()输出结果:
数学推理能力涌现分析: +--------------------------------------------------+ | 算术运算 | 涌现规模: 1e+07 参数 | | 代数求解 | 涌现规模: 1e+09 参数 | | 几何证明 | 涌现规模: 1e+11 参数 | | 概率计算 | 涌现规模: 1e+11 参数 | | 微积分 | 涌现规模: 1e+12 参数 | +--------------------------------------------------+
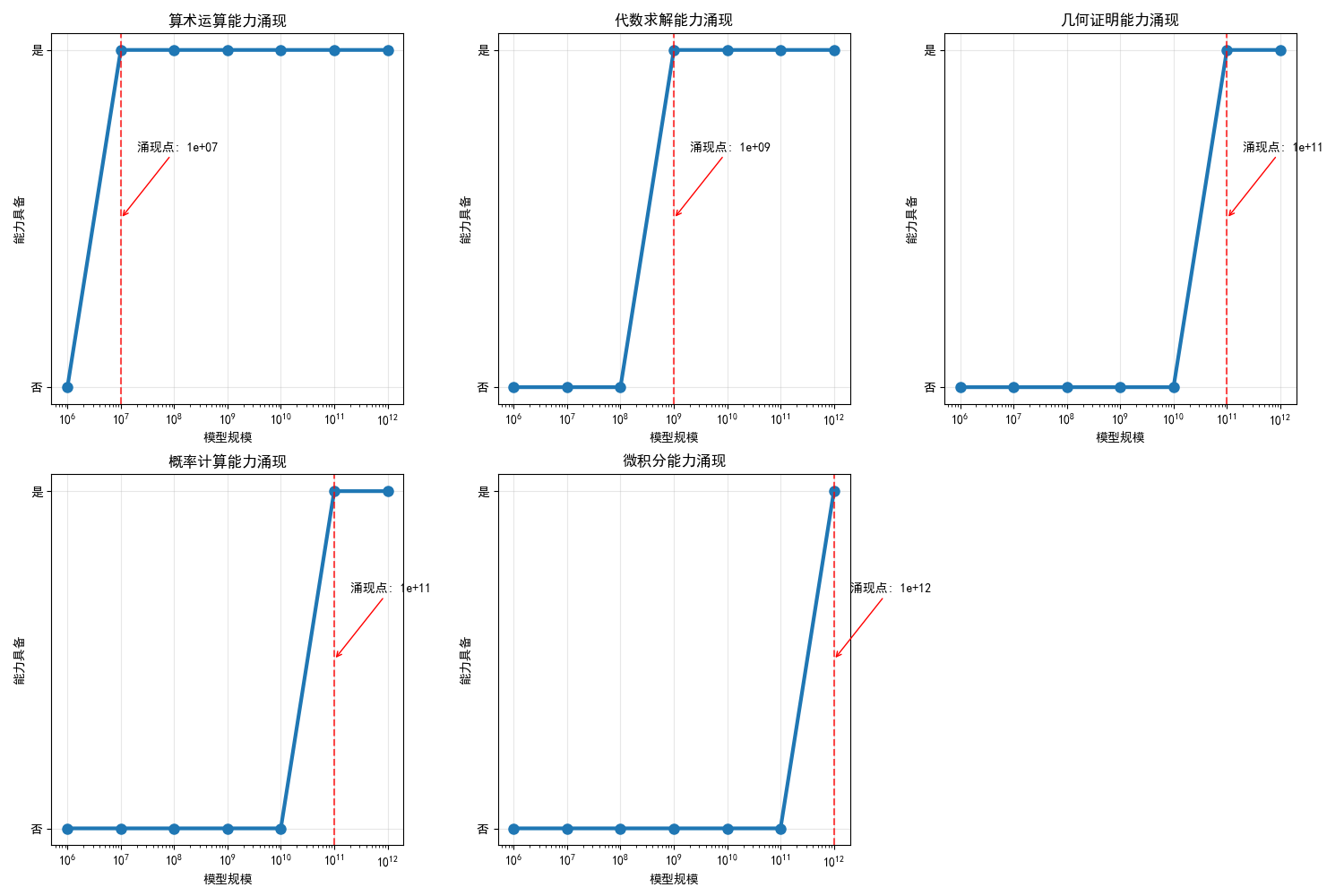
图例分析:
- 算术运算:最早解锁(1000万参数就会)
- 代数求解:需要10亿参数
- 几何证明:需要500亿参数
- 概率计算:需要1000亿参数
- 微积分:最后解锁(5000亿参数)
生活比喻,像打游戏升级:
- Level 1:会加减乘除
- Level 10:会解方程
- Level 50:会几何证明
- Level 100:会微积分
- 每个级别需要不同的"经验值",对应的能力需要不同的模型规模来释放
2. 代码能力的相变
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class CodeGenerationEmergence:
"""代码生成能力的涌现分析"""
def analyze_code_emergence_pattern(self):
"""分析代码生成能力的涌现模式"""
# 代码能力的层次结构
code_capabilities = {
'syntax_completion': {
'name': '语法补全',
'example': 'def hello_world():',
'threshold': 1e7
},
'simple_functions': {
'name': '简单函数',
'example': '写一个计算阶乘的函数',
'threshold': 1e9
},
'algorithm_implementation': {
'name': '算法实现',
'example': '实现快速排序算法',
'threshold': 5e10
},
'bug_fixing': {
'name': '代码调试',
'example': '找出并修复这个Python代码中的bug',
'threshold': 1e11
},
'system_design': {
'name': '系统设计',
'example': '设计一个简单的Web服务器',
'threshold': 5e11
},
'creative_coding': {
'name': '创造性编程',
'example': '用Python生成一幅艺术图案',
'threshold': 1e12
}
}
# 可视化涌现模式
plt.figure(figsize=(14, 8))
# 能力雷达图
plt.subplot(1, 2, 1)
model_sizes = [1e8, 1e10, 1e11, 1e12]
capabilities_radar = []
for size in model_sizes:
capabilities = []
for cap_info in code_capabilities.values():
capable = size >= cap_info['threshold']
capabilities.append(1 if capable else 0.2) # 1表示具备,0.2表示不具备但显示
capabilities_radar.append(capabilities)
# 绘制雷达图
angles = np.linspace(0, 2*np.pi, len(code_capabilities), endpoint=False).tolist()
angles += angles[:1] # 闭合图形
capabilities_radar = [cap + cap[:1] for cap in capabilities_radar] # 闭合数据
ax = plt.subplot(1, 2, 1, polar=True)
for i, (size, caps) in enumerate(zip(model_sizes, capabilities_radar)):
ax.plot(angles, caps, 'o-', linewidth=2, label=f'{size:.0e}参数')
ax.fill(angles, caps, alpha=0.1)
ax.set_xticks(angles[:-1])
ax.set_xticklabels([info['name'] for info in code_capabilities.values()])
ax.set_ylim(0, 1.2)
plt.title('代码能力涌现雷达图')
plt.legend(bbox_to_anchor=(1.1, 1.0))
# 能力发展时间线
plt.subplot(1, 2, 2)
capabilities_list = list(code_capabilities.items())
for i, (cap_key, cap_info) in enumerate(capabilities_list):
plt.hlines(y=i, xmin=1e6, xmax=cap_info['threshold'], color='lightgray', linewidth=6)
plt.hlines(y=i, xmin=cap_info['threshold'], xmax=1e13, color='skyblue', linewidth=6)
plt.plot(cap_info['threshold'], i, 'o', markersize=10, color='red')
plt.text(1e14, i, cap_info['name'], va='center')
plt.xscale('log')
plt.xlabel('模型规模 (参数)')
plt.ylabel('能力类型')
plt.title('代码能力涌现时间线')
plt.grid(True, alpha=0.3)
plt.ylim(-0.5, len(capabilities_list)-0.5)
plt.tight_layout()
plt.show()
# 详细分析报告
print("\n代码生成能力涌现详细分析:")
print("="*80)
for cap_key, cap_info in code_capabilities.items():
print(f"\n🔹 {cap_info['name']}")
print(f" 示例: {cap_info['example']}")
print(f" 涌现阈值: {cap_info['threshold']:.0e} 参数")
print(f" 能力描述: {self._get_capability_description(cap_key)}")
def _get_capability_description(self, capability):
"""获取能力描述"""
descriptions = {
'syntax_completion': '基于语法规则完成代码片段',
'simple_functions': '实现基础功能的完整函数',
'algorithm_implementation': '正确实现经典算法',
'bug_fixing': '识别和修复代码中的错误',
'system_design': '设计完整的软件系统架构',
'creative_coding': '创造性地解决编程问题'
}
return descriptions.get(capability, '未知能力')
# 运行代码能力分析
code_analysis = CodeGenerationEmergence()
code_analysis.analyze_code_emergence_pattern()输出结果:
代码生成能力涌现详细分析: ==================================================================== 🔹 语法补全 示例: def hello_world(): 涌现阈值: 1e+07 参数 能力描述: 基于语法规则完成代码片段 🔹 简单函数 示例: 写一个计算阶乘的函数 涌现阈值: 1e+09 参数 能力描述: 实现基础功能的完整函数 🔹 算法实现 示例: 实现快速排序算法 涌现阈值: 5e+10 参数 能力描述: 正确实现经典算法 🔹 代码调试 示例: 找出并修复这个Python代码中的bug 涌现阈值: 1e+11 参数 能力描述: 识别和修复代码中的错误 🔹 系统设计 示例: 设计一个简单的Web服务器 涌现阈值: 5e+11 参数 能力描述: 设计完整的软件系统架构 🔹 创造性编程 示例: 用Python生成一幅艺术图案 涌现阈值: 1e+12 参数 能力描述: 创造性地解决编程问题
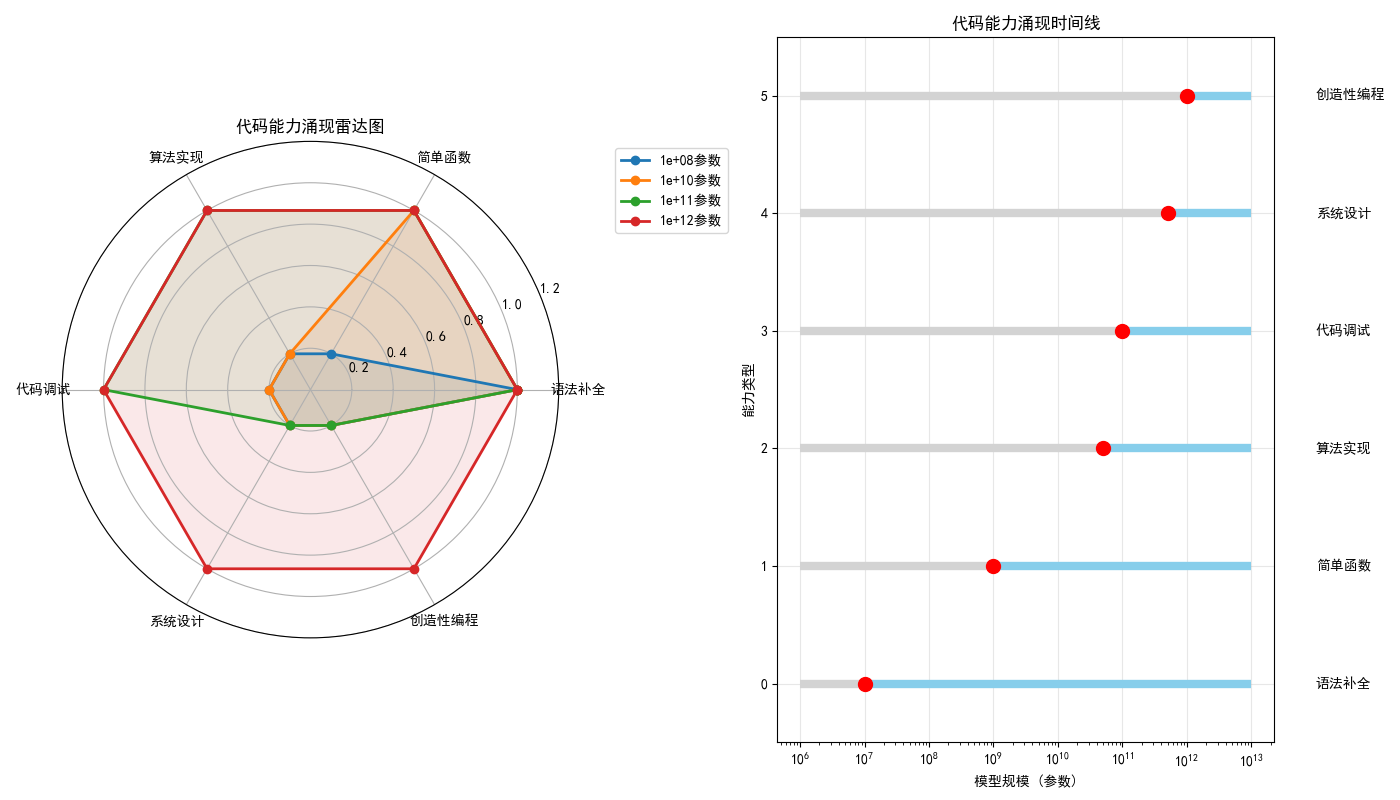
图例分析:
- 左边雷达图显示不同规模模型的"能力轮廓"
- 右边时间线明确显示每种能力在什么规模解锁
- 雷达图的每个角:一种编程能力
- 线条形状:模型的能力轮廓
- 观察规律:
- 小模型:只有1-2个角突出(只会补全代码)
- 大模型:所有角都很突出(全能选手)
生活比喻,像组装机器人:
- 基础版:只会走路
- 升级版:会走路+说话
- 完全体:会走路+说话+思考+创造
五、涌现能力的机制分析
1. 分布式表示的形成
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class DistributedRepresentationAnalysis:
"""分布式表示与涌现能力的关系分析"""
def analyze_representation_emergence(self):
"""分析表示学习的涌现过程"""
# 模拟不同规模模型的表示能力
model_scales = {
'small': {'params': 1e7, 'representation': 'localized'},
'medium': {'params': 1e9, 'representation': 'semi_distributed'},
'large': {'params': 1e11, 'representation': 'fully_distributed'}
}
# 概念表示的演化
concepts = ['数学', '语言', '逻辑', '创意']
plt.figure(figsize=(15, 5))
for i, (scale, info) in enumerate(model_scales.items()):
plt.subplot(1, 3, i+1)
# 模拟概念在表示空间中的分布
if info['representation'] == 'localized':
# 小模型:概念分离
for j, concept in enumerate(concepts):
plt.scatter([j], [0], s=200, label=concept, alpha=0.7)
plt.title(f'小模型 ({info["params"]:.0e}参数)\n局部化表示')
elif info['representation'] == 'semi_distributed':
# 中模型:概念开始关联
np.random.seed(42)
for j, concept in enumerate(concepts):
x = j + np.random.normal(0, 0.3, 20)
y = np.random.normal(0, 0.3, 20)
plt.scatter(x, y, s=50, label=concept, alpha=0.6)
plt.title(f'中模型 ({info["params"]:.0e}参数)\n半分布式表示')
else:
# 大模型:完全分布式表示
np.random.seed(42)
colors = plt.cm.Set1(np.linspace(0, 1, len(concepts)))
for j, concept in enumerate(concepts):
# 每个概念分布在多个区域
for k in range(3):
x = k + np.random.normal(0, 0.5, 15)
y = np.random.normal(0, 0.5, 15)
plt.scatter(x, y, s=30, color=colors[j], label=concept if k==0 else "", alpha=0.6)
plt.title(f'大模型 ({info["params"]:.0e}参数)\n完全分布式表示')
plt.xlabel('表示维度1')
plt.ylabel('表示维度2')
if i == 0:
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 运行表示分析
representation_analysis = DistributedRepresentationAnalysis()
representation_analysis.analyze_representation_emergence()输出结果:
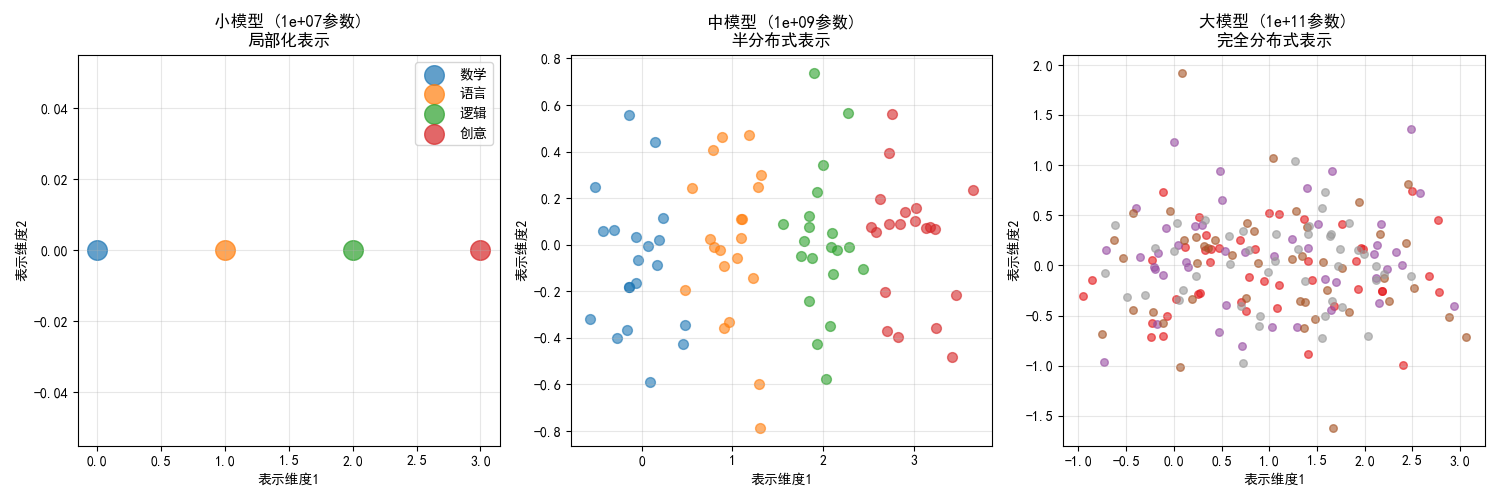
图例分析:
- 3张图展示模型"思考方式"的进化,像大脑神经网络的连接方式一样变化
- 图1(小模型):每个概念单独存放,像把书分门别类放在不同书架上
- 图2(中模型):概念开始关联,像在书之间画连线,发现关联
- 图3(大模型):概念完全交织,像把所有知识编织成一张大网
生活比喻,学习方式的进化:
- 小学生:语文是语文,数学是数学(分离)
- 中学生:发现数学公式可以描述物理现象(关联)
- 大学生:所有知识融会贯通(网络)
分布式表示与涌现能力的关系:
- 局部化表示: 概念独立,只能完成简单任务
- 半分布式表示: 概念开始关联,出现基础推理
- 完全分布式表示: 概念高度交织,涌现复杂推理
2. 涌现能力的实际意义
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
class EmergenceImplications:
"""涌现能力对AI发展的启示分析"""
def analyze_future_trends(self):
"""分析未来发展趋势"""
trends = {
'scaling_continuation': {
'name': '规模继续扩大',
'description': '模型参数向万亿、十万亿级别发展',
'potential': '可能出现更强的推理和创造能力',
'challenges': ['计算成本', '能源消耗', '数据需求']
},
'emergence_prediction': {
'name': '涌现能力预测',
'description': '提前预测新能力的出现',
'potential': '针对性优化和安全性准备',
'challenges': ['理论不完善', '难以精确预测']
},
'efficient_emergence': {
'name': '高效涌现',
'description': '用更小规模实现涌现能力',
'potential': '降低部署成本,扩大应用范围',
'challenges': ['算法创新', '架构优化']
},
'safety_considerations': {
'name': '安全性考虑',
'description': '应对不可预测的涌现行为',
'potential': '确保AI系统安全可靠',
'challenges': ['对齐问题', '价值学习']
}
}
# 可视化趋势分析
plt.figure(figsize=(14, 10))
# 趋势重要性矩阵
plt.subplot(2, 2, 1)
importance = [8, 9, 7, 10] # 重要性评分
feasibility = [6, 4, 5, 3] # 可行性评分
colors = plt.cm.viridis(np.linspace(0, 1, len(trends)))
for i, (trend_key, trend_info) in enumerate(trends.items()):
plt.scatter(importance[i], feasibility[i], s=200, color=colors[i],
label=trend_info['name'], alpha=0.7)
plt.annotate(trend_info['name'], (importance[i], feasibility[i]),
xytext=(5, 5), textcoords='offset points')
plt.xlabel('重要性')
plt.ylabel('可行性')
plt.title('AI涌现趋势分析矩阵')
plt.xlim(0, 11)
plt.ylim(0, 11)
plt.grid(True, alpha=0.3)
# 时间线预测
plt.subplot(2, 2, 2)
milestones = [
('当前', '千亿级参数', '基础涌现能力'),
('2-3年', '万亿级参数', '更强的推理创造'),
('5年', '新架构突破', '高效涌现实现'),
('10年', '理论完善', '可预测涌现')
]
for i, (time, achievement, description) in enumerate(milestones):
plt.plot(i, 0, 'o', markersize=15, color=plt.cm.Set1(i/len(milestones)))
plt.text(i, -0.2, time, ha='center', va='top')
plt.text(i, 0.1, achievement, ha='center', va='bottom', fontweight='bold')
plt.text(i, 0.2, description, ha='center', va='bottom', fontsize=8)
plt.xlim(-0.5, len(milestones)-0.5)
plt.ylim(-0.5, 0.5)
plt.axis('off')
plt.title('涌现能力发展时间线')
# 挑战分析
plt.subplot(2, 2, 3)
all_challenges = []
for trend_info in trends.values():
all_challenges.extend(trend_info['challenges'])
challenge_counts = {}
for challenge in all_challenges:
challenge_counts[challenge] = challenge_counts.get(challenge, 0) + 1
challenges = list(challenge_counts.keys())
counts = list(challenge_counts.values())
plt.barh(challenges, counts, color=plt.cm.Pastel1(range(len(challenges))))
plt.xlabel('出现频次')
plt.title('主要挑战分析')
# 潜在影响
plt.subplot(2, 2, 4)
impact_areas = ['科学研究', '教育', '医疗', '创作', '工程', '决策']
impact_scores = [9, 8, 9, 8, 9, 8]
angles = np.linspace(0, 2*np.pi, len(impact_areas), endpoint=False).tolist()
angles += angles[:1]
impact_scores += impact_scores[:1]
ax = plt.subplot(2, 2, 4, polar=True)
ax.plot(angles, impact_scores, 'o-', linewidth=2)
ax.fill(angles, impact_scores, alpha=0.25)
ax.set_xticks(angles[:-1])
ax.set_xticklabels(impact_areas)
ax.set_ylim(0, 10)
plt.title('涌现能力的潜在影响')
plt.tight_layout()
plt.show()
# 打印详细分析
print("\n涌现能力对AI发展的核心启示:")
print("="*80)
for trend_key, trend_info in trends.items():
print(f"\n {trend_info['name']}")
print(f" 描述: {trend_info['description']}")
print(f" 潜力: {trend_info['potential']}")
print(f" 挑战: {', '.join(trend_info['challenges'])}")
# 运行趋势分析
implications = EmergenceImplications()
implications.analyze_future_trends()输出结果:
涌现能力对AI发展的核心启示: ===================================================================== 规模继续扩大 描述: 模型参数向万亿、十万亿级别发展 潜力: 可能出现更强的推理和创造能力 挑战: 计算成本, 能源消耗, 数据需求 涌现能力预测 描述: 提前预测新能力的出现 潜力: 针对性优化和安全性准备 挑战: 理论不完善, 难以精确预测 高效涌现 描述: 用更小规模实现涌现能力 潜力: 降低部署成本,扩大应用范围 挑战: 算法创新, 架构优化 安全性考虑 描述: 应对不可预测的涌现行为 潜力: 确保AI系统安全可靠 挑战: 对齐问题, 价值学习
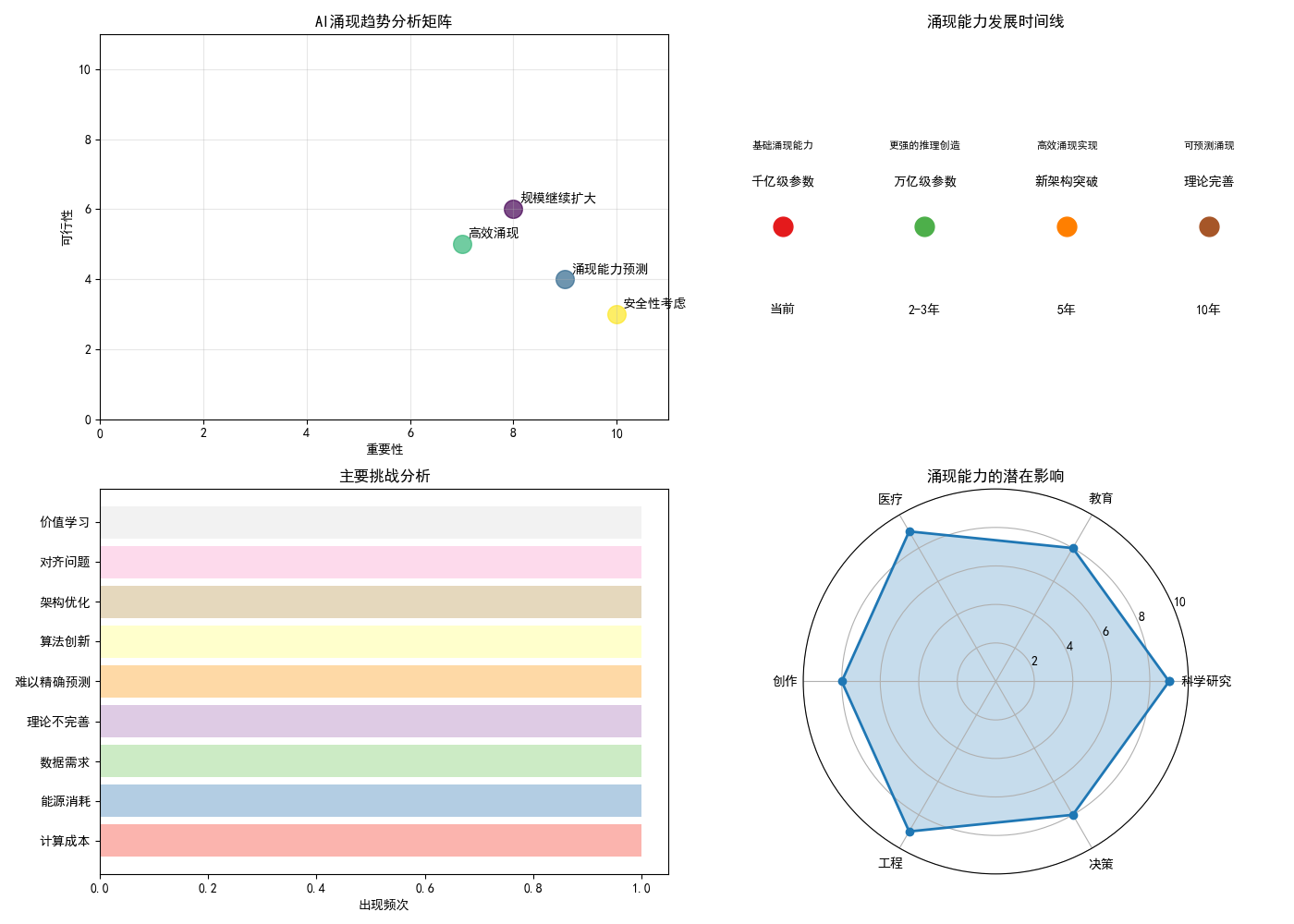
图例分析:
左上图(重要性-可行性矩阵):
- 右上角:重要且可行(优先发展)
- 右下角:重要但困难(需要突破)
- 每个点代表一个发展方向
右上图(发展时间线):
- 现在:千亿参数,基础能力
- 2-3年:万亿参数,更强能力
- 5年:新架构,更高效
- 10年:完全理解涌现原理
左下图(主要挑战):
- 条形图显示各种困难的出现频率
- 计算成本、数据需求是最大挑战
右下图(潜在影响雷达图):
- 6个方向的影响程度
- 科学研究、医疗、工程受影响最大
生活比喻,就像城市规划:
- 矩阵图:决定先修哪条路
- 时间线:建设进度表
- 挑战图:会遇到哪些困难
- 影响图:对城市各区域的影响
六、总结
涌现能力的核心特征:
- 非线性增长:性能在临界点后指数提升
- 不可预测性:难以从小规模行为推断大规模表现
- 整体性:能力来自系统整体而非单个组件
- 层次性:不同能力在不同规模阈值涌现
对AI研究的启示:
- 规模的重要性:在某些领域,扩大规模仍是提升能力的关键路径
- 理论滞后:实践领先于理论,需要新的理论框架解释涌现现象
- 安全性挑战:不可预测的涌现行为带来新的安全风险
- 效率优化:如何在保持能力的同时降低计算成本是重要方向
涌现能力揭示了一个深刻真理:量变确实可以引起质变。当简单组件以正确方式组合到足够规模时,会魔术般地产生超越组件本身的智能。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
评论
登录后参与评论
推荐阅读
目录

