文档建议反馈控制台
首页
学习
活动
专区
圈层
工具
MCP广场
文章/答案/技术大牛
发布
社区首页 >专栏 >《信号与系统》- 第二章 连续系统的时域分析

《信号与系统》- 第二章 连续系统的时域分析

作者头像
啊阿狸不会拉杆
发布于 2026-01-21 11:50:10
发布于 2026-01-21 11:50:10
1020
举报

2.1 LTI 连续系统的响应

一、微分方程的经典解

        LTI 连续系统可以用常系数线性微分方程描述：

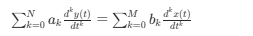
经典解分为齐次解和特解：

  • 齐次解：满足齐次方程的解，对应系统自由响应
  • 特解：满足非齐次方程的解，对应系统强迫响应
代码语言：javascript
复制
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 定义微分方程：y''(t) + 3y'(t) + 2y(t) = x(t)
def system_ode(t, y, x_func):
    """
    定义系统的微分方程
    y: [y, y']
    返回: [y', y'']
    """
    dydt = np.zeros_like(y)
    dydt[0] = y[1]  # y'
    dydt[1] = -3*y[1] - 2*y[0] + x_func(t)  # y'' = -3y' - 2y + x(t)
    return dydt

# 输入信号：阶跃函数 u(t)
def x(t):
    return np.heaviside(t, 1)

# 初始条件
y0 = [0, 0]  # y(0-), y'(0-)

# 求解微分方程
t_span = [0, 10]  # 时间范围
t_eval = np.linspace(0, 10, 1000)  # 评估点
sol = solve_ivp(lambda t, y: system_ode(t, y, x), t_span, y0, t_eval=t_eval)

# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(sol.t, sol.y[0], 'b-', label='系统响应 y(t)')
plt.plot(sol.t, x(sol.t), 'r--', label='输入信号 x(t)')
plt.title('LTI系统的阶跃响应')
plt.xlabel('时间 t')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()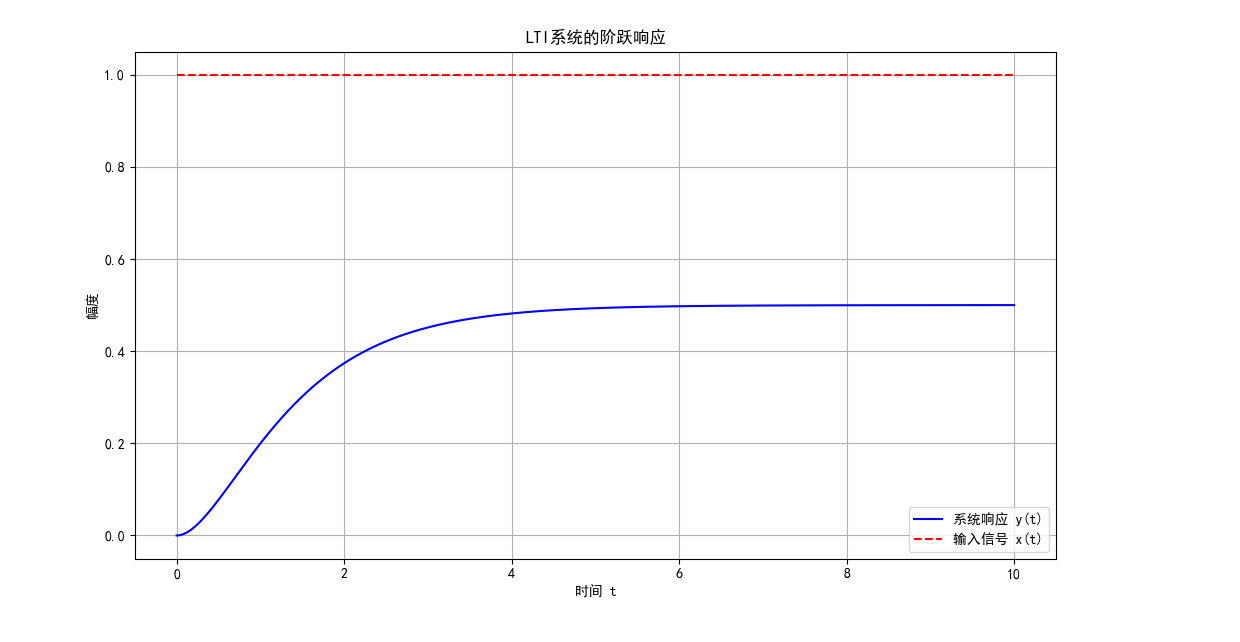

图 1：LTI 系统的阶跃响应

二、关于 0- 与 0+ 值

  • 0-：输入加入前的瞬间，初始条件
  • 0+：输入加入后的瞬间，可能发生跳变
  • 冲激函数可能导致 0 - 到 0 + 的跳变
代码语言：javascript
复制
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 定义微分方程：y''(t) + 3y'(t) + 2y(t) = x(t)
def system_ode(t, y, x_func):
    """
    定义系统的微分方程
    y: [y, y']
    返回: [y', y'']
    """
    dydt = np.zeros_like(y)
    dydt[0] = y[1]  # y'
    dydt[1] = -3*y[1] - 2*y[0] + x_func(t)  # y'' = -3y' - 2y + x(t)
    return dydt

# 时间范围和评估点
t_span = [0, 10]  # 时间范围
t_eval = np.linspace(0, 10, 1000)  # 评估点

# 计算0-到0+的跳变
# 对于方程 y'' + 3y' + 2y = δ(t)，当y(0-)=0, y'(0-)=0时
# 两边积分得 y'(0+) - y'(0-) = 1，故y'(0+)=1

# 重新求解，考虑跳变
y0_plus = [0, 1]  # y(0+)=0, y'(0+)=1
sol_jump = solve_ivp(lambda t, y: system_ode(t, y, lambda t: 0), t_span, y0_plus, t_eval=t_eval)

plt.figure(figsize=(10, 6))
plt.plot(sol_jump.t, sol_jump.y[0], 'g-', label='冲激响应 h(t)')
plt.title('系统对冲激输入的响应（考虑0+跳变）')
plt.xlabel('时间 t')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()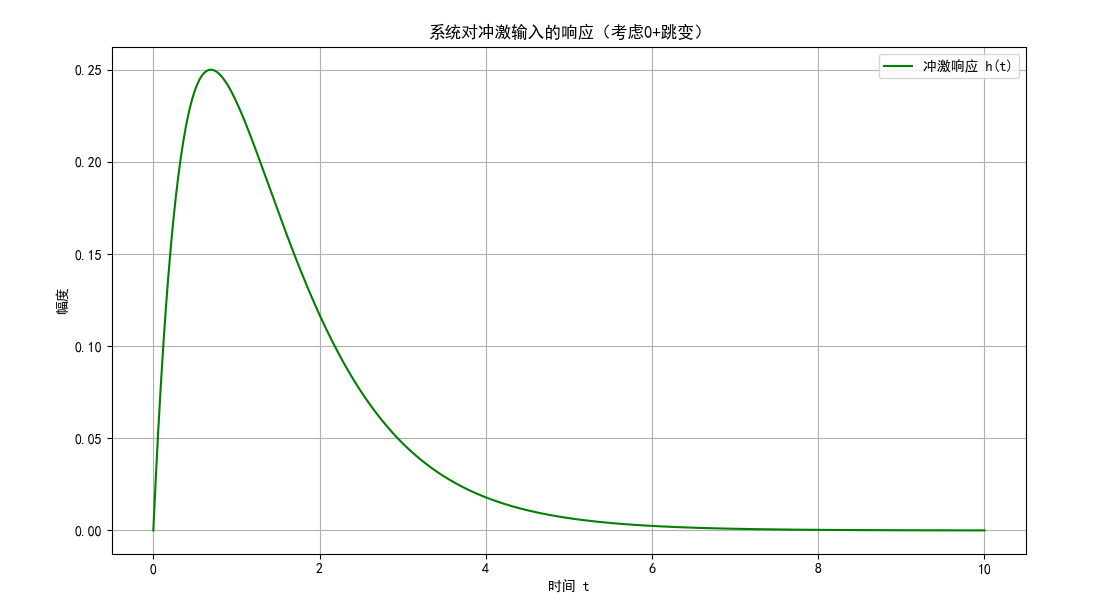

图 2：考虑 0 + 跳变的系统响应

代码语言：javascript
复制
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
import numpy as np

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 定义系统微分方程
def system_ode(t, y, x_func):
    """
    定义系统的微分方程: y'' + 3y' + 2y = x(t)
    y: [y, y']
    返回: [y', y'']
    """
    dydt = np.zeros_like(y)
    dydt[0] = y[1]  # y'
    dydt[1] = -3*y[1] - 2*y[0] + x_func(t)  # y'' = -3y' - 2y + x(t)
    return dydt

# 定义输入信号（阶跃函数）
def x(t):
    """输入信号: 阶跃函数 u(t)"""
    return np.heaviside(t, 1)

# 设置时间范围
t_span = [0, 10]  # 时间范围
t_eval = np.linspace(0, 10, 1000)  # 评估点

# 计算零输入响应、零状态响应和全响应
# 系统特征根：r^2 + 3r + 2 = 0 => r1=-1, r2=-2
# 零输入响应：y_zi(t) = C1e^(-t) + C2e^(-2t)
# 初始条件：y(0+)=1, y'(0+)=2
# 解得：C1=4, C2=-3

def y_zi(t):
    """零输入响应"""
    return 4*np.exp(-t) - 3*np.exp(-2*t)

# 零状态响应（数值解）
sol_zs = solve_ivp(lambda t, y: system_ode(t, y, x), t_span, [0, 0], t_eval=t_eval)

# 全响应
y_total = y_zi(sol_zs.t) + sol_zs.y[0]

plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
plt.plot(sol_zs.t, y_zi(sol_zs.t), 'r-', label='零输入响应')
plt.legend()
plt.grid(True)

plt.subplot(3, 1, 2)
plt.plot(sol_zs.t, sol_zs.y[0], 'g-', label='零状态响应')
plt.legend()
plt.grid(True)

plt.subplot(3, 1, 3)
plt.plot(sol_zs.t, y_total, 'b-', label='全响应')
plt.legend()
plt.grid(True)
plt.xlabel('时间 t')
plt.tight_layout()
plt.show()

图 3：零输入响应、零状态响应和全响应对比

2.2 冲激响应和阶跃响应

一、冲激响应

        冲激响应 h (t)：系统对单位冲激输入 δ(t) 的零状态响应

代码语言：javascript
复制
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 系统传递函数：H(s) = 1/(s^2 + 3s + 2)
num = [1]  # 分子系数
den = [1, 3, 2]  # 分母系数

# 计算冲激响应
t_impulse = np.linspace(0, 10, 1000)
t_impulse, h = signal.impulse((num, den), T=t_impulse)

plt.figure(figsize=(10, 6))
plt.plot(t_impulse, h, 'b-', label='冲激响应 h(t)')
plt.title('系统的冲激响应')
plt.xlabel('时间 t')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()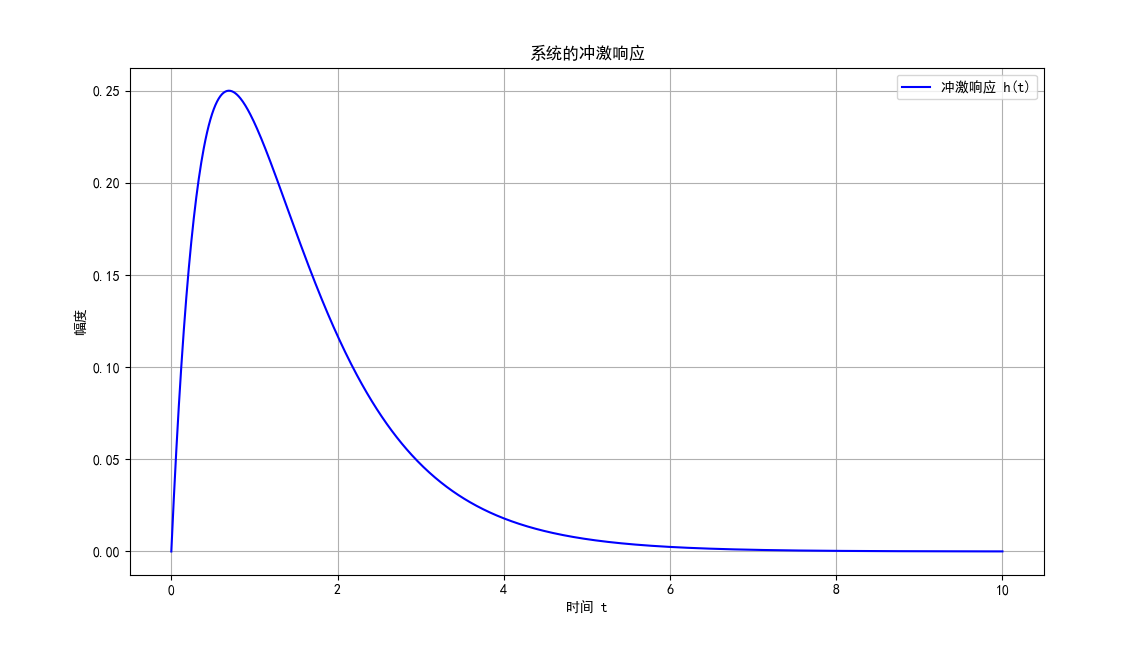

图 4：系统的冲激响应

二、阶跃响应

        阶跃响应 s (t)：系统对单位阶跃输入 u (t) 的零状态响应

代码语言：javascript
复制
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 系统传递函数：H(s) = 1/(s^2 + 3s + 2)
num = [1]  # 分子系数
den = [1, 3, 2]  # 分母系数

# 计算阶跃响应
t_step = np.linspace(0, 10, 1000)
t_step, s = signal.step((num, den), T=t_step)

plt.figure(figsize=(10, 6))
plt.plot(t_step, s, 'r-', label='阶跃响应 s(t)')
plt.title('系统的阶跃响应')
plt.xlabel('时间 t')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()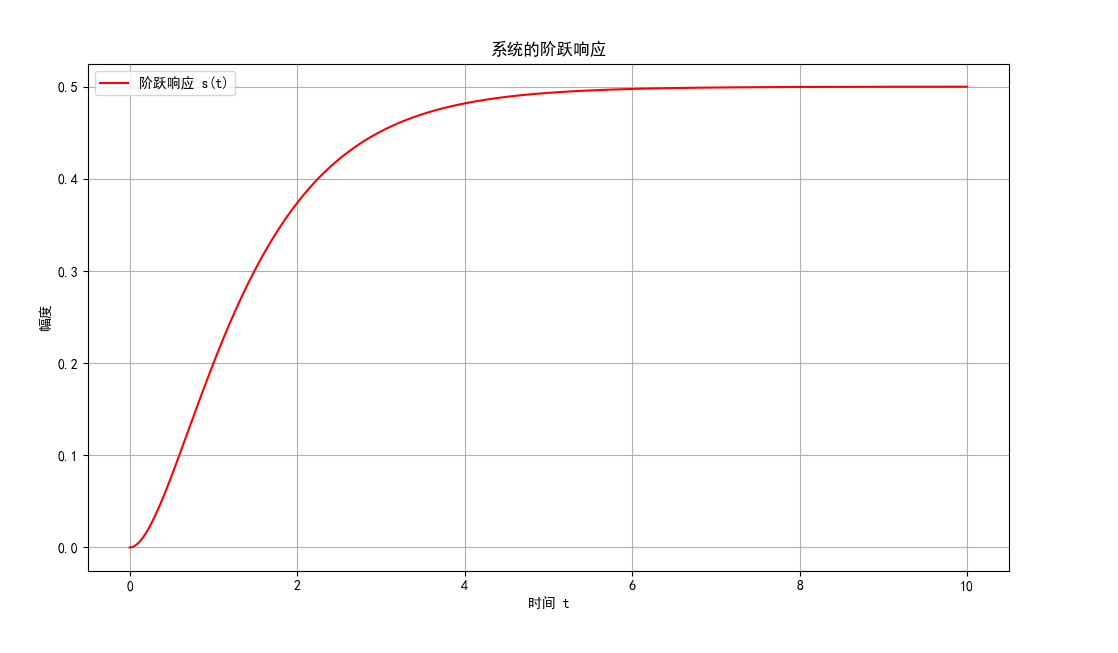

图 5：系统的阶跃响应

2.3 零状态响应与卷积积分

一、任意激励下的零状态响应

零状态响应可表示为输入信号与冲激响应的卷积：

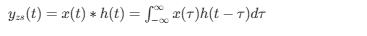
二、卷积积分

代码语言：javascript
复制
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 卷积积分示例
def x(t):
    """矩形脉冲信号"""
    return np.where((t >= 0) & (t <= 2), 1, 0)

def h(t):
    """指数衰减冲激响应"""
    return np.where(t >= 0, np.exp(-t), 0)

# 计算卷积
dt = 0.01
t = np.arange(-5, 10, dt)
x_vals = x(t)
h_vals = h(t)

# 使用numpy的convolve函数
y_conv = np.convolve(x_vals, h_vals, mode='same') * dt

plt.figure(figsize=(12, 10))
plt.subplot(3, 1, 1)
plt.plot(t, x_vals, 'b-', label='输入信号 x(t)')
plt.legend()
plt.grid(True)

plt.subplot(3, 1, 2)
plt.plot(t, h_vals, 'r-', label='冲激响应 h(t)')
plt.legend()
plt.grid(True)

plt.subplot(3, 1, 3)
plt.plot(t, y_conv, 'g-', label='卷积结果 y(t) = x(t)*h(t)')
plt.legend()
plt.grid(True)
plt.xlabel('时间 t')
plt.tight_layout()
plt.show()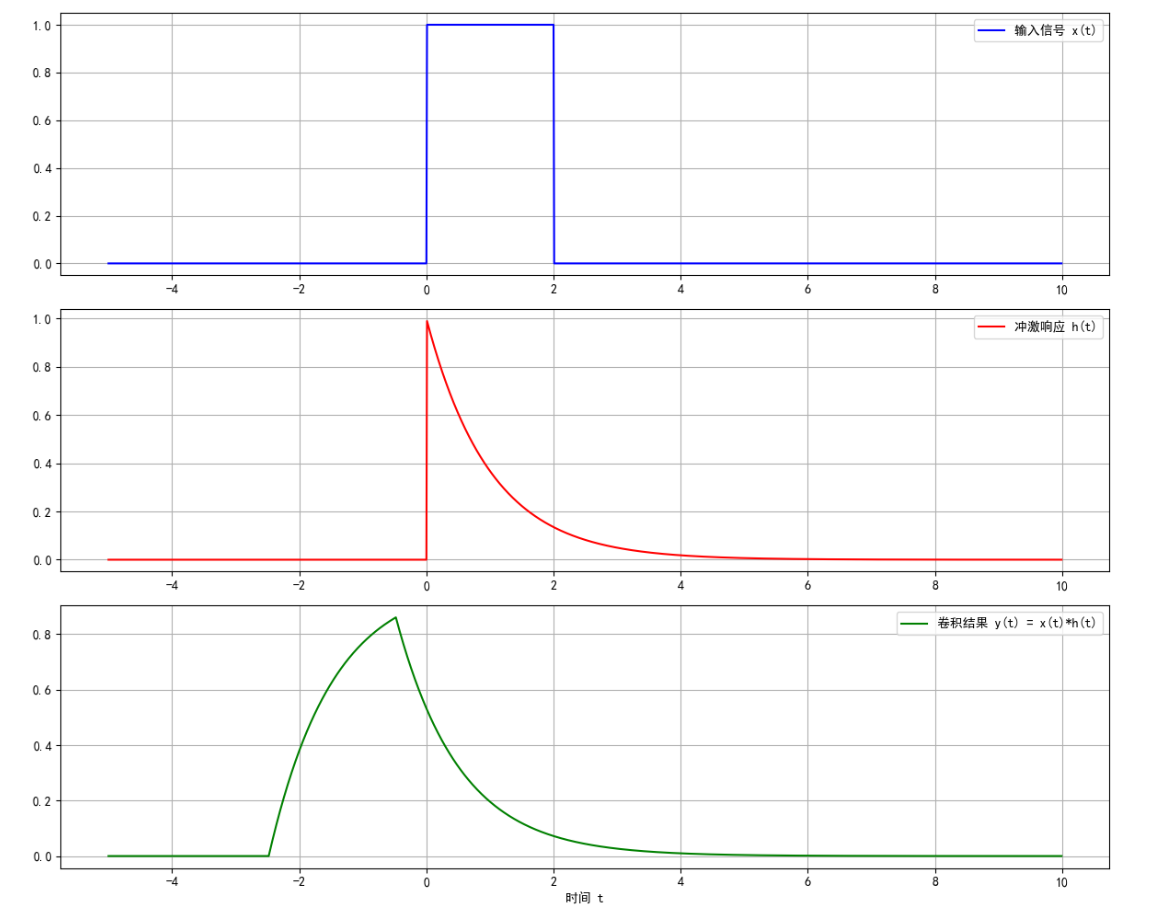

图 6：卷积积分示例

2.4 卷积积分的性质

一、卷积的代数运算

代码语言：javascript
复制
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 定义信号函数
def x(t):
    """矩形脉冲信号"""
    return np.where((t >= 0) & (t <= 2), 1, 0)

def h(t):
    """指数衰减冲激响应"""
    return np.where(t >= 0, np.exp(-t), 0)

# 计算卷积
dt = 0.01
t = np.arange(-5, 10, dt)
x_vals = x(t)
h_vals = h(t)

# 验证卷积交换律
# 计算 x(t)*h(t) 和 h(t)*x(t)
y_conv1 = np.convolve(x_vals, h_vals, mode='same') * dt
y_conv2 = np.convolve(h_vals, x_vals, mode='same') * dt

# 计算误差
error = np.max(np.abs(y_conv1 - y_conv2))
print(f"卷积交换律验证误差: {error:.10f}")

plt.figure(figsize=(10, 6))
plt.plot(t, y_conv1, 'b-', label='x(t)*h(t)')
plt.plot(t, y_conv2, 'r--', label='h(t)*x(t)')
plt.title(f'卷积交换律验证 (误差: {error:.10f})')
plt.xlabel('时间 t')
plt.ylabel('幅度')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()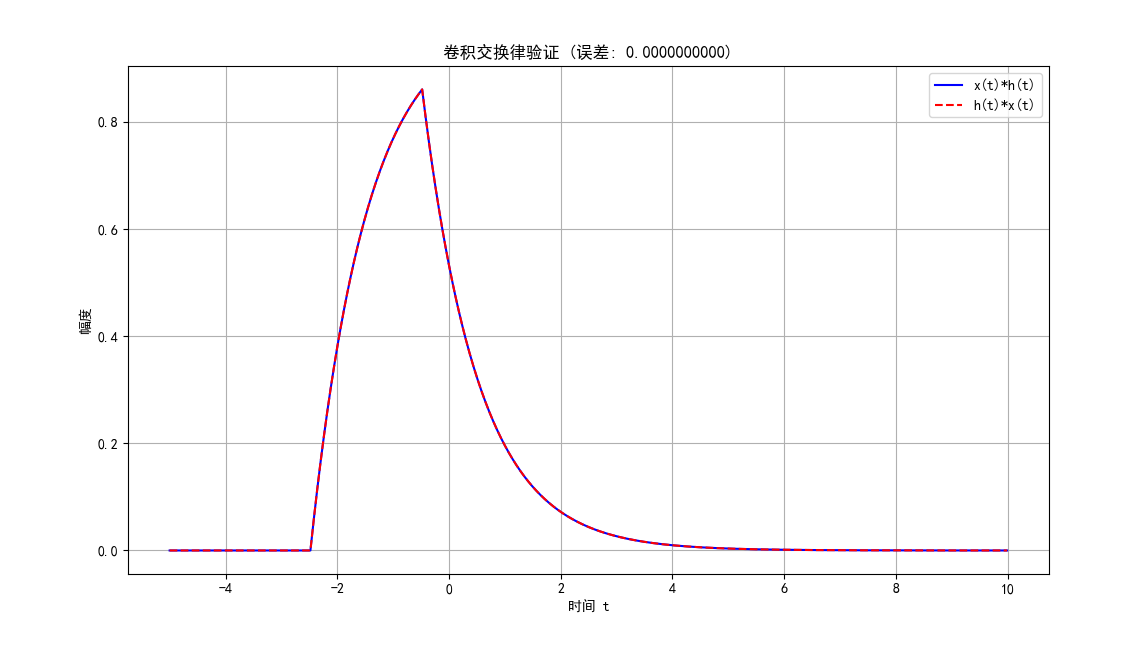

图 7：卷积交换律验证

二、函数与冲激函数的卷积

代码语言：javascript
复制
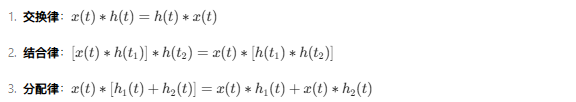
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 定义信号函数
def x(t):
    """矩形脉冲信号"""
    return np.where((t >= 0) & (t <= 2), 1, 0)

def delta_approx(t, t0=0, width=0.02):
    """近似冲激函数"""
    return np.where(np.abs(t-t0) < width/2, 1/width, 0)

# 计算卷积
dt = 0.01
t = np.arange(-5, 10, dt)
x_vals = x(t)

# 函数与冲激函数的卷积示例
t0 = 1  # 冲激函数的位置
delta_vals = delta_approx(t, t0)  # 近似冲激函数
y_conv_delta = np.convolve(x_vals, delta_vals, mode='same') * dt  # 计算卷积

plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
plt.plot(t, x_vals, 'b-', label='x(t)')
plt.legend()
plt.grid(True)

plt.subplot(3, 1, 2)
plt.plot(t, delta_vals, 'r-', label='δ(t-1) (近似)')
plt.legend()
plt.grid(True)

plt.subplot(3, 1, 3)
plt.plot(t, y_conv_delta, 'g-', label='x(t) * δ(t-1) = x(t-1)')
plt.plot(t, x(t-t0), 'k--', label='理论值 x(t-1)')
plt.legend()
plt.grid(True)
plt.xlabel('时间 t')
plt.tight_layout()
plt.show()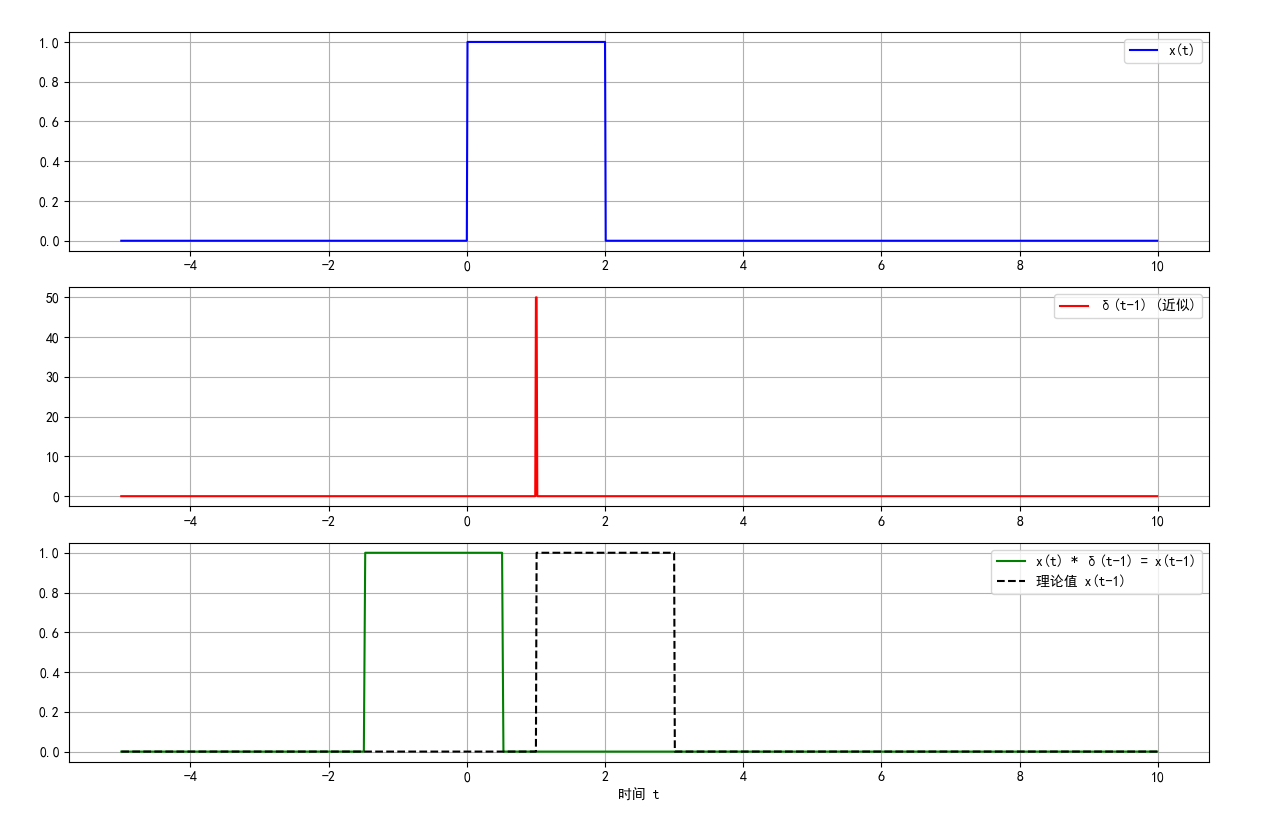

图 8：函数与冲激函数的卷积

三、卷积的微分与积分

代码语言：javascript
复制
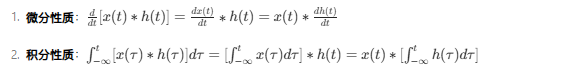
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 定义信号函数
def x(t):
    """矩形脉冲信号"""
    return np.where((t >= 0) & (t <= 2), 1, 0)

def h(t):
    """指数衰减冲激响应"""
    return np.where(t >= 0, np.exp(-t), 0)

# 计算卷积
dt = 0.01
t = np.arange(-5, 10, dt)
x_vals = x(t)
h_vals = h(t)

# 卷积的微分性质验证
# 计算导数
dx_dt = np.gradient(x_vals, dt)
dh_dt = np.gradient(h_vals, dt)

# 计算卷积
y_conv_dx = np.convolve(dx_dt, h_vals, mode='same') * dt
y_conv_dh = np.convolve(x_vals, dh_dt, mode='same') * dt

plt.figure(figsize=(12, 8))
plt.subplot(2, 1, 1)
plt.plot(t, y_conv_dx, 'b-', label='dx/dt * h(t)')
plt.legend()
plt.grid(True)

plt.subplot(2, 1, 2)
plt.plot(t, y_conv_dh, 'r-', label='x(t) * dh/dt')
plt.plot(t, y_conv_dx, 'g--', label='dx/dt * h(t) (参考)')
plt.legend()
plt.grid(True)
plt.xlabel('时间 t')
plt.tight_layout()
plt.show()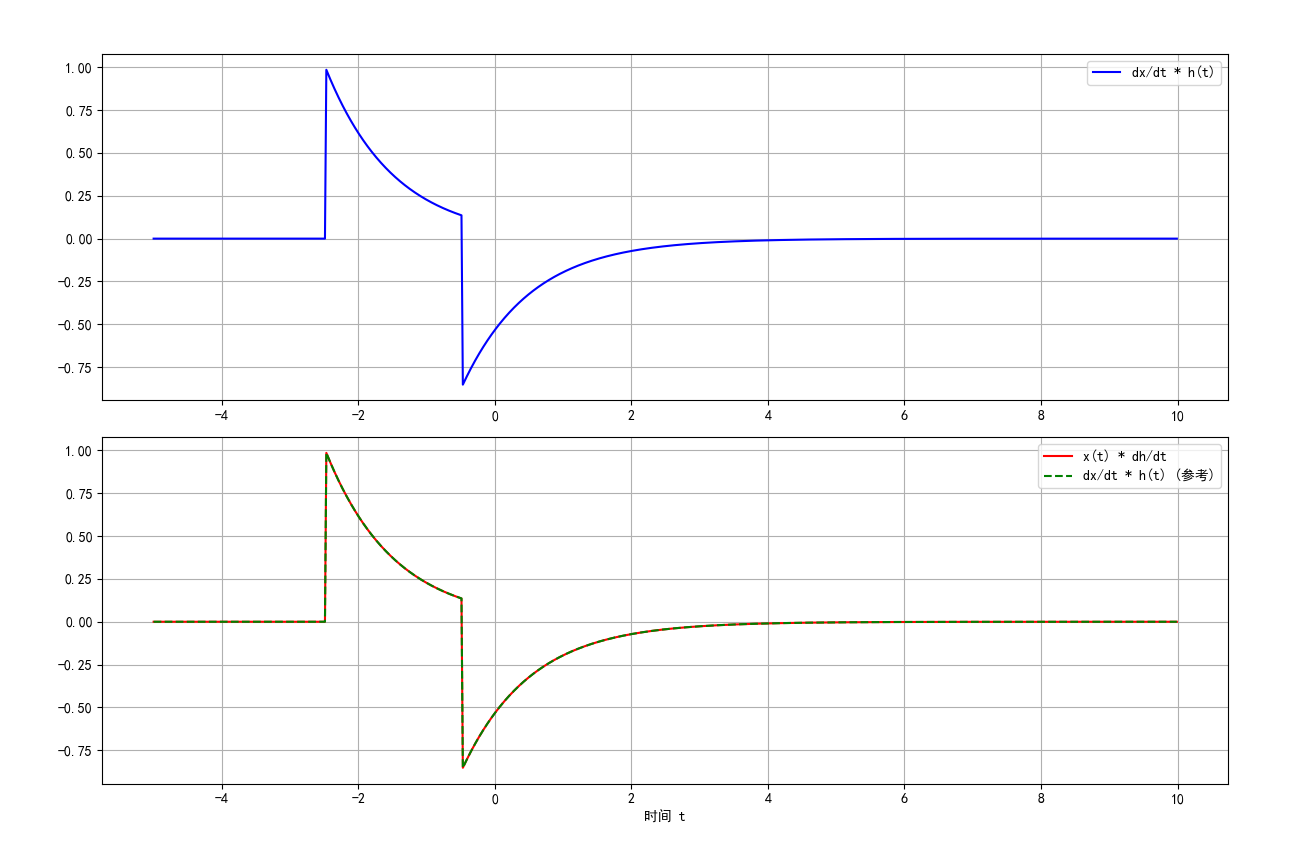

图 9：卷积的微分性质验证

四、相关函数

代码语言：javascript
复制
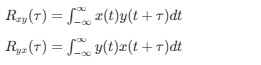
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 定义信号函数
def x(t):
    """矩形脉冲信号"""
    return np.where((t >= 0) & (t <= 2), 1, 0)

def h(t):
    """指数衰减冲激响应"""
    return np.where(t >= 0, np.exp(-t), 0)

# 计算相关函数
def correlate(x, y, mode='same'):
    """计算相关函数 R_xy(τ)"""
    return np.correlate(x, y, mode=mode)

# 计算卷积和相关
dt = 0.01
t = np.arange(-5, 10, dt)
x_vals = x(t)
h_vals = h(t)

# 计算自相关和互相关
R_xx = correlate(x_vals, x_vals, mode='same') * dt
R_xy = correlate(x_vals, h_vals, mode='same') * dt
R_yx = correlate(h_vals, x_vals, mode='same') * dt
R_yy = correlate(h_vals, h_vals, mode='same') * dt

# 构建相关时间轴
tau = np.arange(-len(t)//2, len(t)//2) * dt

plt.figure(figsize=(12, 10))
plt.subplot(2, 2, 1)
plt.plot(tau, R_xx, 'b-', label='R_xx(τ)')
plt.title('x(t)的自相关函数')
plt.xlabel('τ')
plt.legend()
plt.grid(True)

plt.subplot(2, 2, 2)
plt.plot(tau, R_xy, 'r-', label='R_xy(τ)')
plt.title('x(t)与h(t)的互相关函数')
plt.xlabel('τ')
plt.legend()
plt.grid(True)

plt.subplot(2, 2, 3)
plt.plot(tau, R_yx, 'g-', label='R_yx(τ)')
plt.title('h(t)与x(t)的互相关函数')
plt.xlabel('τ')
plt.legend()
plt.grid(True)

plt.subplot(2, 2, 4)
plt.plot(tau, R_yy, 'm-', label='R_yy(τ)')
plt.title('h(t)的自相关函数')
plt.xlabel('τ')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()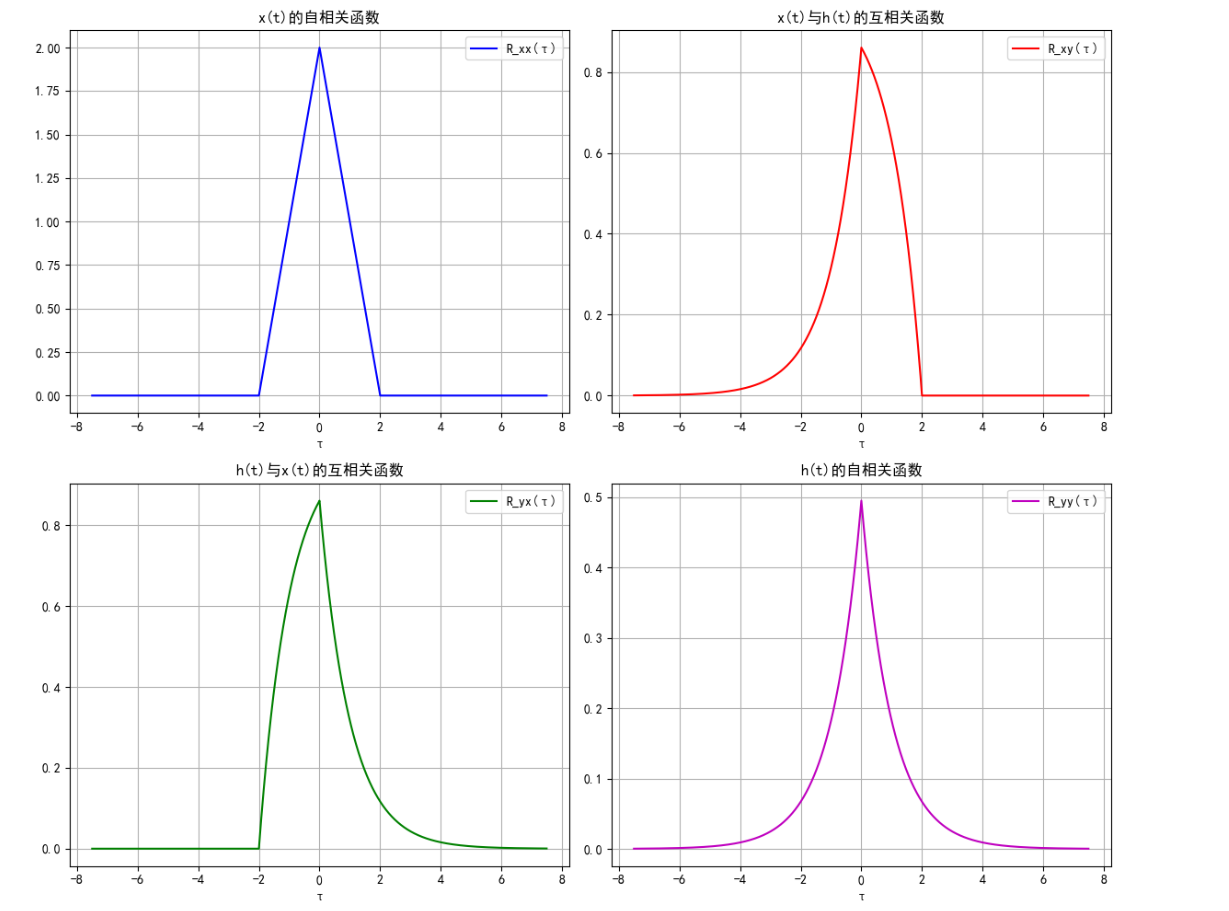

图 10：相关函数计算结果

LTI 系统时域分析思维导图

图 11：LTI 系统时域分析思维导图

        通过本章学习，我们掌握了 LTI 连续系统的时域分析方法，包括微分方程求解、零输入响应与零状态响应的计算、冲激响应与阶跃响应的概念，以及卷积积分及其性质。这些方法为后续频域和复频域分析奠定了基础。

本文参与 腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。
原始发表：2026-01-20，如有侵权请联系 cloudcommunity@tencent.com 删除
系统
dt
import
label
函数

本文分享自 作者个人站点/博客 前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与 腾讯云自媒体同步曝光计划  ，欢迎热爱写作的你一起参与！

系统
dt
import
label
函数
评论
登录后参与评论
0 条评论
热度
最新
登录 后参与评论
推荐阅读
目录
  • 2.1 LTI 连续系统的响应
    • 一、微分方程的经典解
    • 二、关于 0- 与 0+ 值
  • 2.2 冲激响应和阶跃响应
    • 一、冲激响应
    • 二、阶跃响应
  • 2.3 零状态响应与卷积积分
    • 一、任意激励下的零状态响应
    • 二、卷积积分
  • 2.4 卷积积分的性质
    • 一、卷积的代数运算
    • 二、函数与冲激函数的卷积
    • 三、卷积的微分与积分
    • 四、相关函数
    • LTI 系统时域分析思维导图
领券

腾讯云开发者

扫码关注腾讯云开发者

扫码关注腾讯云开发者

领取腾讯云代金券

热门产品

热门推荐

更多推荐

Copyright © 2013 - 2026 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有 

深圳市腾讯计算机系统有限公司 ICP备案/许可证号：粤B2-20090059 粤公网安备44030502008569号

腾讯云计算（北京）有限责任公司 京ICP证150476号 |  京ICP备11018762号

问题归档专栏文章快讯文章归档关键词归档开发者手册归档开发者手册 Section 归档

Copyright © 2013 - 2026 Tencent Cloud.

All Rights Reserved. 腾讯云 版权所有

登录 后参与评论