【算法基础篇】（五十八）线性代数之高斯消元法从原理到实战：手撕模板 + 洛谷真题全解

前言

在算法竞赛和工程数学中，求解线性方程组是高频问题，而高斯消元法正是解决这一问题的经典核心算法。它不仅能高效求解 n 元线性方程组，还能延伸应用到行列式计算、矩阵求逆、n 维球形空间球心求解等场景，是线性代数在算法领域的重要落地工具。本文将从线性方程组的基础概念出发，一步步拆解高斯消元法的原理、初等行变换规则、解的判定方法，再结合多道经典真题，实现从原理到 C++ 代码模板的完整落地，让零基础的同学也能彻底掌握高斯消元法！下面就让我们正式开始吧！

一、前置基础：线性方程组与矩阵的关联

要理解高斯消元法，首先要建立线性方程组和矩阵之间的联系，将方程组转化为矩阵形式是高斯消元的第一步，也是核心前提。

1.1 线性方程组的定义

由 n 个 m 元一次方程组成的方程组，称为n 元线性方程组（本文主要讨论 n 个 n 元的情况，即方程数 = 未知数个数），其标准形式为：

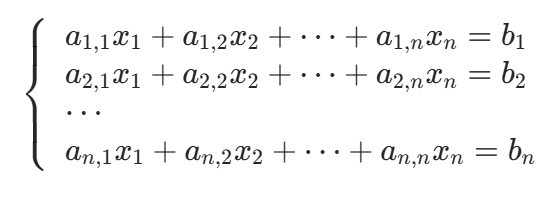
其中x1​,x2​,...,xn​是待求解的未知数，ai,j​是第 i 个方程中xj​的系数，bi​是第 i 个方程的常数项。

1.2 系数矩阵与增广矩阵

为了简化线性方程组的求解过程，我们可以将方程组的系数和常数项提取出来，组成特殊的矩阵，这也是高斯消元法的操作对象：

1. 系数矩阵：仅由方程组中未知数的系数构成的 n×n 矩阵，只保留ai,j​部分；
2. 增广矩阵：将系数矩阵和常数项列拼接而成的 n×(n+1) 矩阵，是高斯消元法的核心操作矩阵，包含了方程组的所有求解信息。

示例：对于三元线性方程组

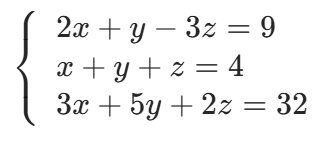
• 系数矩阵：

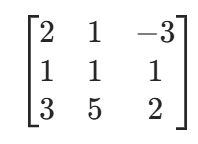
• 增广矩阵：​

​​

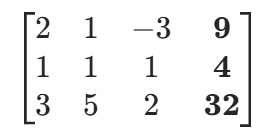
增广矩阵的最后一列是方程组的常数项，这一列也是最终求解的关键 —— 当增广矩阵转化为简化阶梯型后，最后一列就是未知数的解。

二、高斯消元法核心原理：初等行变换与阶梯型矩阵

高斯消元法的本质是通过矩阵的初等行变换，将增广矩阵转化为阶梯型矩阵（或简化阶梯型矩阵），进而通过回代或直接读取得到方程组的解。整个过程就像解一元一次方程的 “消元” 思路，通过消去未知数，将复杂的 n 元方程组转化为易求解的形式。

2.1 矩阵的初等行变换

对增广矩阵执行的初等行变换是高斯消元法的基础，这三种变换不会改变方程组的解，也是我们化简矩阵的唯一手段，必须牢记：

1. 交换两行：将矩阵的第 i 行和第 j 行交换位置，记为ri​↔rj​；
2. 某行乘非零常数：将矩阵的第 i 行所有元素乘以一个非零常数 k，记为ri​×k；
3. 某行的 k 倍加到另一行：将矩阵第 i 行的 k 倍加到第 j 行对应元素上，记为rj​+k×ri​。

这三种变换的核心目的是消去未知数的系数，让矩阵呈现出 “阶梯状” 的结构，方便后续求解。

2.2 阶梯型矩阵与简化阶梯型矩阵

高斯消元法的目标是将增广矩阵转化为阶梯型矩阵，进一步可转化为简化阶梯型矩阵，后者能直接读取解，是最理想的形式。

1. 阶梯型矩阵：矩阵的非零行从上到下，主元（每行第一个非零元素）的列标依次递增，呈 “阶梯状”，下方全为 0 行；
2. 简化阶梯型矩阵：在阶梯型矩阵的基础上，满足主元为 1，且主元所在列的其他元素均为 0，此时增广矩阵的最后一列就是未知数的解，无需回代。

2.3 高斯消元法的完整步骤（手算版）

以三元方程组的增广矩阵为例，手把手演示高斯消元法的手算步骤，分为消元阶段（转化为阶梯型）和回代 / 化简阶段（转化为简化阶梯型），理解手算过程是编写代码的关键。

原始增广矩阵：

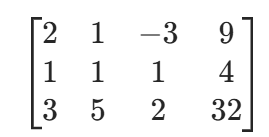
阶段 1：消元 —— 转化为阶梯型矩阵

1. 交换 1、2 行（让第一列主元更简单，方便计算）：r1​↔r2​​

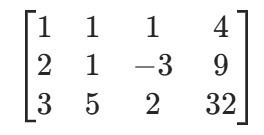
1. 消去第一列下方元素：r2​−2r1​、r3​−3r1​​

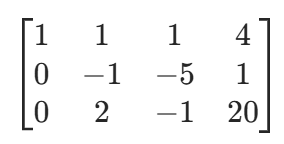
1. 第二行乘 - 1（主元化为正）：r2​×(−1)​

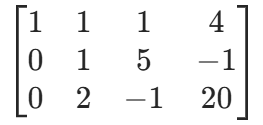
1. 消去第二列下方元素：r3​−2r2

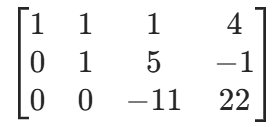
1. 第三行除以 - 11（主元化为 1）：r3​÷(−11)

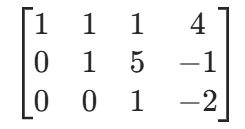
​​此时矩阵已成为阶梯型矩阵，可通过回代法求解：从最后一行z=−2代入上一行，依次求出y、x。

阶段 2：化简 —— 转化为简化阶梯型矩阵

为了直接读取解，继续对阶梯型矩阵做初等行变换，消去主元上方的元素：

1. 消去第三列上方元素：r2​−5r3​、r1​−r3​​

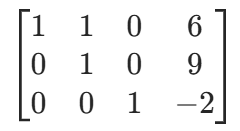
1. 消去第二列上方元素：r1​−r2​​

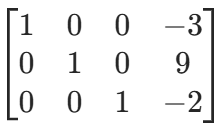
至此得到简化阶梯型矩阵，直接读取解即可，整个过程无需求解复杂的方程，这就是高斯消元法的高效性。

三、线性方程组的三种解的情况

高斯消元法不仅能求解方程组，还能判定解的存在性和唯一性，线性方程组共有三种解的情况：唯一解、无解、无穷多解，核心通过转化后的增广矩阵判断，这也是算法编程中的重点和难点。

3.1 唯一解（最理想情况）

判定条件：增广矩阵转化为阶梯型后，非零行的数量 = 未知数的数量，且无矛盾行（0 行对应非零常数）。

本质：方程数足够，且相互独立，能唯一确定每个未知数的值，也是我们最常遇到的情况，如上述的三元方程组。

3.2 无解（矛盾情况）

判定条件：增广矩阵转化为阶梯型后，出现全 0 系数行对应非零常数项的行（即0=k,k=0）。

本质：方程组中存在相互矛盾的方程，无法同时满足，因此无解。

示例：方程组

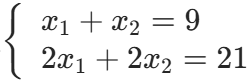
​，其增广矩阵转化后为：

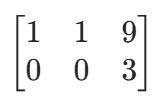
第二行表示0x1​+0x2​=3，显然矛盾，因此方程组无解。

3.3 无穷多解（自由元存在）

判定条件：增广矩阵转化为阶梯型后，非零行的数量 < 未知数的数量，且无矛盾行。

本质：方程数不足，存在自由元（可任意取值的未知数），自由元的个数 = 未知数个数 - 非零行数量，每个自由元取一个值，就能得到一组解，因此有无穷多解。

示例：方程组

，

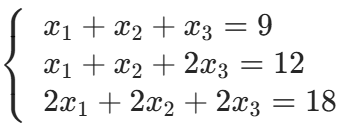
转化后的简化阶梯型矩阵为：​

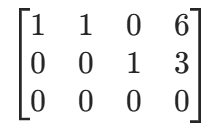
非零行数量 = 2 < 未知数数量 = 3，存在 1 个自由元x2​，解为x1​=6−x2​,x3​=3，x2​可取任意值，对应无穷多解。

3.4 主元与自由元

在判定无穷多解时，主元和自由元是核心概念：

1. 主元：阶梯型矩阵中，每行第一个非零元素所在的列对应的未知数，为主元变量，其值由自由元决定；
2. 自由元：非主元列对应的未知数，为自由变量，可任意取值，是无穷多解的根源。

总结：解的判定是高斯消元法的重要环节，代码中需要先完成矩阵化简，再遍历矩阵判断属于哪种情况，再输出对应结果。

四、高斯消元法的 C++ 通用模板：核心实现

理解了高斯消元法的原理和手算步骤后，接下来实现通用的 C++ 代码模板，这是解决所有高斯消元相关问题的基础。模板的核心是通过编程模拟初等行变换，将增广矩阵转化为简化阶梯型矩阵，再判定解的情况。

4.1 核心思路

1. 浮点数处理：由于消元过程中会出现除法，使用double类型存储矩阵元素，定义极小值eps=1e-7判断浮点数是否为 0（避免精度误差）；
2. 枚举主元列：从小到大枚举每一列（对应每个未知数），作为当前的主元列；
3. 选主元行：在当前主元列中，找到未确定主元的行中绝对值最大的行（选主元，避免除数过小导致精度误差）；
4. 初等行变换：
   • 若主元为 0，说明该列为自由元，跳过；
   • 交换主元行到当前行；
   • 将主元所在行的主元化为 1（整行除以主元）；
   • 消去当前主元列的其他所有行的元素（化为 0）；
5. 解的判定：遍历化简后的矩阵，判断是唯一解、无解还是无穷多解；
6. 输出解：若为唯一解，输出每个未知数的值；否则输出对应判定结果。

4.2 通用 C++ 模板代码

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;

const int N = 110;          // 矩阵最大规模，可根据题目调整
const double eps = 1e-7;    // 浮点数精度，判断是否为0
double a[N][N];             // 存储增广矩阵，n*(n+1)
int n;                      // 未知数的数量

// 判断浮点数是否为0
inline bool is_zero(double x) {
    return fabs(x) < eps;
}

// 高斯消元核心函数，返回值：1-唯一解，0-无解，2-无穷多解
int gauss() {
    // c：当前处理的主元列，r：当前处理的行
    int c, r;
    for (c = 1, r = 1; c <= n; c++) {
        // 步骤1：选主元行，找当前列中绝对值最大的行
        int max_row = r;
        for (int i = r; i <= n; i++) {
            if (fabs(a[i][c]) > fabs(a[max_row][c])) {
                max_row = i;
            }
        }
        // 若主元为0，说明是自由元，跳过当前列
        if (is_zero(a[max_row][c])) continue;
        // 步骤2：交换主元行到当前行
        for (int i = c; i <= n + 1; i++) {
            swap(a[max_row][i], a[r][i]);
        }
        // 步骤3：将主元化为1，整行除以主元
        double div = a[r][c];
        for (int i = c; i <= n + 1; i++) {
            a[r][i] /= div;
        }
        // 步骤4：消去当前列的其他所有行的元素，化为0
        for (int i = 1; i <= n; i++) {
            if (i != r && !is_zero(a[i][c])) {
                double t = a[i][c];
                for (int j = c; j <= n + 1; j++) {
                    a[i][j] -= t * a[r][j];
                }
            }
        }
        r++; // 处理下一行
    }

    // 步骤5：判定解的情况
    // 情况1：无解：存在0行对应非零常数项（0=k, k≠0）
    for (int i = r; i <= n; i++) {
        if (!is_zero(a[i][n + 1])) {
            return 0;
        }
    }
    // 情况2：无穷多解：非零行数量 < 未知数数量
    if (r <= n) {
        return 2;
    }
    // 情况3：唯一解，此时矩阵已是简化阶梯型，直接读取最后一列
    return 1;
}

int main() {
    // 输入：n个未知数，n行，每行n+1个数（系数+常数项）
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n + 1; j++) {
            cin >> a[i][j];
        }
    }

    int res = gauss();
    if (res == 0) {
        cout << "No Solution" << endl;
    } else if (res == 2) {
        cout << "Infinite Solutions" << endl;
    } else {
        // 输出唯一解，保留2位小数（可根据题目调整）
        for (int i = 1; i <= n; i++) {
            printf("%.2lf\n", a[i][n + 1]);
        }
    }

    return 0;
}

4.3 模板关键细节说明

1. 选主元的意义：选择当前列绝对值最大的行作为主元行，避免除数过小导致的精度误差，这是高斯消元法中保证计算精度的关键步骤，不可省略；
2. 浮点数判 0：由于计算机存储浮点数存在精度误差，不能直接用x==0判断，而是通过fabs(x) < eps判断，eps一般取10−7 /10−8；
3. 矩阵下标：代码中矩阵下标从 1 开始，更贴合数学中的矩阵编号习惯，避免下标 0 带来的混淆；
4. 解的判定顺序：先判断无解，再判断无穷多解，最后是唯一解，该顺序能避免判定错误；
5. 精度控制：输出解时使用printf格式化输出，可根据题目要求调整保留的小数位数。

五、洛谷真题实战 1：基础高斯消元（P3389）

题目链接：https://www.luogu.com.cn/problem/P3389

5.1 题目描述

给定 n 元线性方程组，求解该方程组，若不存在唯一解则输出No Solution，若有唯一解则输出每个未知数的值，保留 2 位小数。

• 输入：第一行正整数 n，接下来 n 行每行 n+1 个整数，代表方程组的系数和常数项；
• 输出：有唯一解则输出 n 行，每行一个数（保留 2 位小数），否则输出No Solution。

5.2 解题思路

直接复用通用模板，稍作修改：将高斯消元函数的返回值简化，若主元列出现 0 则直接返回无解，无需判断无穷多解，其余逻辑完全一致。

5.3 题目专属 C++ 代码

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;

const int N = 110;
const double eps = 1e-7;
double a[N][N];
int n;

inline bool is_zero(double x) {
    return fabs(x) < eps;
}

int gauss() {
    int c, r;
    for (c = 1, r = 1; c <= n; c++) {
        int max_row = r;
        for (int i = r; i <= n; i++) {
            if (fabs(a[i][c]) > fabs(a[max_row][c])) {
                max_row = i;
            }
        }
        if (is_zero(a[max_row][c])) return 0; // 无唯一解
        for (int i = c; i <= n + 1; i++) swap(a[max_row][i], a[r][i]);
        double div = a[r][c];
        for (int i = c; i <= n + 1; i++) a[r][i] /= div;
        for (int i = 1; i <= n; i++) {
            if (i != r && !is_zero(a[i][c])) {
                double t = a[i][c];
                for (int j = c; j <= n + 1; j++) {
                    a[i][j] -= t * a[r][j];
                }
            }
        }
        r++;
    }
    return 1; // 有唯一解
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n + 1; j++) {
            cin >> a[i][j];
        }
    }
    if (gauss() == 0) {
        cout << "No Solution" << endl;
    } else {
        for (int i = 1; i <= n; i++) {
            printf("%.2lf\n", a[i][n + 1]);
        }
    }
    return 0;
}

六、洛谷真题实战 2：线性方程组解的判定（P2455）

题目链接：https://www.luogu.com.cn/problem/P2455

6.1 题目描述

给定 n 元线性方程组，根据输入数据输出解的情况：

• 有唯一解：输出每个未知数的值，保留 2 位小数；
• 无解：输出-1；
• 无穷多解：输出0。
• 输入输出格式与基础题一致，核心差异是需要完整判定解的情况。

6.2 解题思路

直接使用本文第四节的通用高斯消元模板，主函数中根据高斯消元函数的返回值（0 - 无解，1 - 唯一解，2 - 无穷多解）输出对应结果即可，无需修改核心逻辑。

6.3 题目专属 C++ 代码

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;

const int N = 55;           // 题目中n≤50，缩小规模
const double eps = 1e-7;
double a[N][N];
int n;

inline bool is_zero(double x) {
    return fabs(x) < eps;
}

int gauss() {
    int c, r;
    for (c = 1, r = 1; c <= n; c++) {
        int max_row = r;
        for (int i = r; i <= n; i++) {
            if (fabs(a[i][c]) > fabs(a[max_row][c])) {
                max_row = i;
            }
        }
        if (is_zero(a[max_row][c])) continue;
        for (int i = c; i <= n + 1; i++) swap(a[max_row][i], a[r][i]);
        double div = a[r][c];
        for (int i = c; i <= n + 1; i++) a[r][i] /= div;
        for (int i = 1; i <= n; i++) {
            if (i != r && !is_zero(a[i][c])) {
                double t = a[i][c];
                for (int j = c; j <= n + 1; j++) {
                    a[i][j] -= t * a[r][j];
                }
            }
        }
        r++;
    }

    // 判定无解
    for (int i = r; i <= n; i++) {
        if (!is_zero(a[i][n + 1])) return 0;
    }
    // 判定无穷多解
    if (r <= n) return 2;
    // 唯一解
    return 1;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n + 1; j++) {
            cin >> a[i][j];
        }
    }

    int res = gauss();
    if (res == 0) {
        cout << -1 << endl;
    } else if (res == 2) {
        cout << 0 << endl;
    } else {
        for (int i = 1; i <= n; i++) {
            printf("x%d=%.2lf\n", i, a[i][n + 1]);
        }
    }

    return 0;
}

七、高斯消元法的进阶应用：矩阵求逆与 n 维球心求解

高斯消元法不仅能求解线性方程组，还能延伸解决矩阵求逆、n 维球形空间球心求解、行列式计算等问题，本文选取了两个经典的算法竞赛真题，讲解高斯消元法的进阶应用，进一步体现其通用性。

7.1 进阶应用 1：矩阵求逆（洛谷 P4783）

题目链接：https://www.luogu.com.cn/problem/P4783

7.1.1 核心原理

对于 n 阶方阵 A，若其可逆（行列式≠0），则可通过高斯 - 约当消元法求其逆矩阵A−1，核心思路是：

1. 构造 n×2n 的增广矩阵[A∣E]，其中 E 是 n 阶单位矩阵；
2. 对增广矩阵执行初等行变换，将左侧的 A 转化为单位矩阵 E；
3. 此时右侧的 E 会同步转化为A−1，即增广矩阵最终变为[E∣A−1]；
4. 若左侧无法转化为 E，说明矩阵 A 不可逆，输出No Solution。

由于题目要求对109+7取模，需使用整数模运算，用快速幂求逆元代替除法（因为模运算中无除法，除以 k 等价于乘以 k 的逆元）。

7.1.2 核心代码要点

1. 用long long存储矩阵元素，避免溢出；
2. 快速幂求逆元：qpow(a, MOD-2, MOD)（费马小定理，MOD 为质数）；
3. 初等行变换中，除法替换为乘以逆元，所有操作均取模；
4. 最终若左侧为单位矩阵，输出右侧的 n×n 矩阵，即为逆矩阵。

7.2 进阶应用 2：n 维球形空间球心求解（洛谷 P4035）

题目链接：https://www.luogu.com.cn/problem/P4035

7.2.1 核心原理

n 维球体的球心(x1​,x2​,...,xn​)满足：球面上任意一点(p1​,p2​,...,pn​)到球心的距离的平方等于半径的平方，即

。

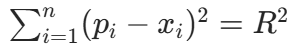
取球面上 n+1 个点，两两作差消去R2，可得到 n 个线性方程，构成 n 元线性方程组，用高斯消元法求解该方程组，即可得到 n 维球心的坐标。

7.2.2 核心代码要点

1. 根据 n+1 个点的坐标，推导出线性方程组的增广矩阵；
2. 直接复用高斯消元法的通用模板，求解该方程组；
3. 输出结果时保留 3 位小数，严格匹配题目精度要求。

这两个应用的核心仍是高斯消元法的初等行变换，只是增广矩阵的构造方式不同，充分说明高斯消元法是线性代数中最通用的算法之一。

总结

高斯消元法看似繁琐，实则有固定的规律和模板，只要掌握了核心的初等行变换和解的判定方法，就能轻松解决各类相关问题。它不仅是算法竞赛的高频考点，也是工程数学、机器学习、数值计算等领域的基础工具，掌握高斯消元法，能为后续的线性代数和算法学习打下坚实的基础。 从线性方程组到矩阵求逆，再到 n 维空间的球心求解，高斯消元法的通用性让我们看到了数学算法的魅力。希望本文能帮助大家从原理到实战，彻底掌握高斯消元法，在算法竞赛和实际应用中灵活运用！