格努图直方图箱除以体积
格努图直方图箱除以体积
提问于 2020-07-06 00:53:20
我模拟球体中的点,半径为1,我在这个卷中生成了1.000.000蒙特卡罗点。为了制作一个gnu图直方图,我计算了每个向量的长度(每个向量长度在0到1之间)。有了100个垃圾箱,直方图看起来就像:图形数据直方图。
如果有人想知道为什么不产生大于0.91的分数,我也不知道,但这不是问题。
这是我的侏儒代码:
n=100 #number of intervals
max=1.0 #max value
min=0.0 #min value
width=(max-min)/n #interval width
#function used to map a value to the intervals
hist(x,width)=width*floor(x/width)+width/2.0
#settings
set xlabel "Radius"
set ylabel "Primarys/Intervall"
set xrange [-0.1:1.1]
set yrange [0:32000]
set boxwidth width*0.8
set style fill solid 0.5 #fillstyle
set tics out nomirror
#plot
plot "primaryPosition(1).csv" u (hist($1,width)):(1.0) smooth freq w boxes lc rgb"green"一般情况下:体积由r^3增长到半径r。
在我的时频图中,每个球壳都是一个桶,而桶数是100。因此,随着桶数的增加,每个螺旋壳的体积呈立方体增长( r^3)。从这个角度看,直方图看起来不错。
但是我想要做的是绘制每个体积点的密度:点/壳体积。
这应该是从球体中心到它的边界的线性分布。
我怎样才能告诉gnuplot除以其相应的体积,这取决于每个球壳的外部和内部半径?
公式为:(4/3)pi(R^3-r^3),R外半径和r内半径为a壳。
回答 1
Stack Overflow用户
发布于 2020-07-06 22:16:12
下面的示例创建一些随机测试数据(应该是20'000均匀分布的随机点)。一种可能是,您首先通过绑定到一个表来创建直方图数据,然后再将其除以shell的体积。
顺便说一句,球体外壳的体积是(4./3)*pi*(R**3-r**3),而不是你给出的公式。你为什么要设置max < min?也许你想根据你的具体需要来调整你的装订。
代码:
### histogram normalized by sphere shell volume
reset session
set view equal xyz
# create some test data
set print $Data
do for [i=1:20000] {
x = rand(0)*2-1
y = rand(0)*2-1
z = rand(0)*2-1
r = sqrt(x**2 + y**2 + z**2)
if (r <= 1) { print sprintf("%g %g %g %g",x,y,z,r) }
}
set print
n = 100 # number of intervals
min = 0.0 # max value
max = 1.0 # min value
myWidth=(max-min)/n # interval width
bin(x)=myWidth*floor(x/myWidth)
ShellVolume(r) = (4./3)*pi*((r+myWidth)**3-r**3)
set boxwidth myWidth absolute
set table $Histo
plot $Data u (bin($4)):(1) smooth freq
unset table
set multiplot layout 2,1
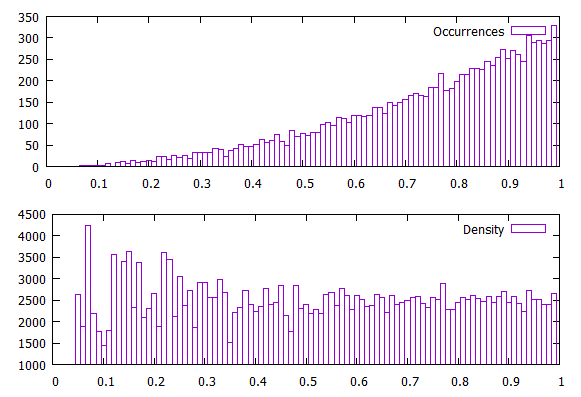
plot $Histo u 1:2 w boxes ti "Occurrences"
plot $Histo u 1:($2/ShellVolume($1)) w boxes ti "Density"
unset multiplot
### end of code结果:
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/62752467
复制相关文章
相似问题
