混合高斯混合模型的mle2/Optim算法
我有一个mle2模型,我在这里开发就是为了演示这个问题。我从两个独立的高斯分布x1和x2生成值,将它们组合在一起形成x=c(x1,x2),然后创建一个MLE,它试图通过xsplit参数将x值重新分类为属于特定x值的左边或特定x值的右侧。
问题是所发现的参数并不理想。具体来说,xsplit总是以其起始值的形式返回。如果我改变它的起始值(例如,4或9),结果的日志可能性就会有很大的差异。
下面是一个完全可复制的例子:
set.seed(1001)
library(bbmle)
x1 = rnorm(n=100,mean=4,sd=0.8)
x2 = rnorm(n=100,mean=12,sd=0.4)
x = c(x1,x2)
hist(x,breaks=20)
ff = function(m1,m2,sd1,sd2,xsplit) {
outs = rep(NA,length(xvals))
for(i in seq(1,length(xvals))) {
if(xvals[i]<=xsplit) {
outs[i] = dnorm(xvals[i],mean=m1,sd=sd1,log=T)
}
else {
outs[i] = dnorm(xvals[i],mean=m2,sd=sd2,log=T)
}
}
-sum(outs)
}
# change xsplit starting value here to 9 and 4
# and realize the difference in log likelihood
# Why isn't mle finding the right value for xsplit?
mo = mle2(ff,
start=list(m1=1,m2=2,sd1=0.1,sd2=0.1,xsplit=9),
data=list(xvals=x))
#print mo to see log likelihood value
mo
#plot the result
c=coef(mo)
m1=as.numeric(c[1])
m2=as.numeric(c[2])
sd1=as.numeric(c[3])
sd2=as.numeric(c[4])
xsplit=as.numeric(c[5])
leftx = x[x<xsplit]
rightx = x[x>=xsplit]
y1=dnorm(leftx,mean=m1,sd=sd1)
y2=dnorm(rightx,mean=m2,sd=sd2)
points(leftx,y1*40,pch=20,cex=1.5,col="blue")
points(rightx,y2*90,pch=20,cex=1.5,col="red")如何修改我的mle2以捕获正确的参数,特别是对于xsplit
回答 1
Stack Overflow用户
发布于 2014-02-07 09:35:49
混合模型带来了许多技术挑战(组件重新命名下的对称性,等等);除非您有非常具体的需求,否则最好使用为R编写的大量特殊用途混合建模包中的一个(仅为library("sos"); findFn("{mixture model}")或findFn("{mixture model} Gaussian"))。
然而,在这种情况下,您有一个更具体的问题,即xsplit参数的拟合优度/似然面是“坏”的(即导数几乎处处为零)。特别是,如果您考虑数据集中相邻的一对点x1,x2,则x1和x2之间的任何分裂参数的可能性完全相同(因为这些值中的任何一个都将数据集分割成相同的两个组件)。这意味着可能性表面是分段平坦的,这使得任何明智的优化器--甚至是那些不明显依赖衍生品的Nelder-几乎不可能实现。您的选择是:(1)使用某种蛮力的随机优化器(如optim()中的method="SANN“);(2)将xsplit从函数和剖面中取出来(即对xsplit的每一种可能的选择进行优化,对其他四个参数进行优化);(3)平滑您的分裂准则(即拟合属于某个组件的逻辑概率);(4)使用一种特殊用途的混合模型拟合算法,正如上面所建议的那样。
set.seed(1001)
library(bbmle)
x1 = rnorm(n=100,mean=4,sd=0.8)
x2 = rnorm(n=100,mean=12,sd=0.4)
x = c(x1,x2)您的ff函数可以编写得更简洁:
## ff can be written more compactly:
ff2 <- function(m1,m2,sd1,sd2,xsplit) {
p <- xvals<=xsplit
-sum(dnorm(xvals,mean=ifelse(p,m1,m2),
sd=ifelse(p,sd1,sd2),log=TRUE))
}
## ML estimation
mo <- mle2(ff2,
start=list(m1=1,m2=2,sd1=0.1,sd2=0.1,xsplit=9),
data=list(xvals=x))
## refit with a different starting value for xsplit
mo2 <- update(mo,start=list(m1=1,m2=2,sd1=0.1,sd2=0.1,xsplit=4))
## not used here, but maybe handy
plotfun <- function(mo,xvals=x,sizes=c(40,90)) {
c <- coef(mo)
hist(xvals,col="gray")
p <- xvals <= c["xsplit"]
y <- with(as.list(coef(mo)),
dnorm(xvals,mean=ifelse(p,m1,m2),
sd=ifelse(p,sd1,sd2))*sizes[ifelse(p,1,2)])
points(xvals,y,pch=20,cex=1.5,col=c("blue","red")[ifelse(p,1,2)])
}
plot(slice(mo),ylim=c(-0.5,10))
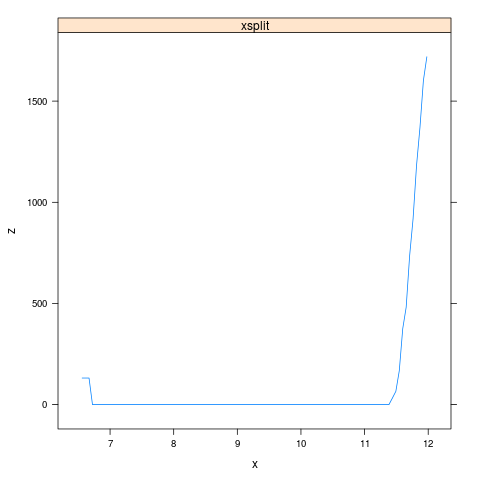
plot(slice(mo2),ylim=c(-0.5,10))我稍微欺骗了一下,只提取了xsplit参数:
xsplit=9周围似然曲面
xsplit=4周围似然曲面
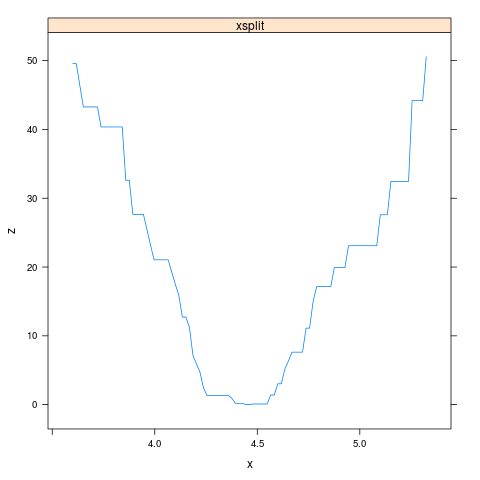
更新:平滑
正如我前面提到的,一种解决方案是使两个混合组分之间的边界光滑或逐渐,而不是锐利。我使用了一个逻辑函数plogis(),中点在xsplit,标度任意设置为2(您可以尝试使它变得更清晰;原则上您可以使它成为一个可调整的参数,但是如果这样做,您可能会再次遇到麻烦,因为优化器可能希望使其无限.)换句话说,如果说x<xsplit的所有观测都在组件1中,x>xsplit的所有观测肯定在组件2中,那么我们就会说,等于xsplit的观测值在任何一个分量中都有50/50的下降概率,并且随着xsplit以下的x值的减少,组件1中的观测量肯定会增加。具有非常大的缩放参数的逻辑函数近似于以前尝试过的尖分裂模型;通常,您希望使缩放参数“足够大”,以得到合理的分割,并且足够小,不会遇到数值问题。(如果比例过大,计算出的概率将下降到0或1,您就会回到开始的地方.)
这是我的第二次或第三次尝试;我不得不做相当大的修改(将值从0或介于0到1之间,并在一个日志标度上拟合标准差),但结果似乎是合理的。如果我在logistic (plogis)函数上不使用plogis,那么我得到0或1的概率;如果我在正常概率上不使用clamp() (单边),那么它们就可以向下流动到零--在任何情况下,我都得到无限的或NaN的结果。在日志标度上拟合标准差会更好,因为当优化器尝试标准差的负值时,不会遇到问题。
## bound x values between lwr and upr
clamp <- function(x,lwr=0.001,upr=0.999) {
pmin(upr,pmax(lwr,x))
}
ff3 <- function(m1,m2,logsd1,logsd2,xsplit) {
p <- clamp(plogis(2*(xvals-xsplit)))
-sum(log((1-p)*clamp(dnorm(xvals,m1,exp(logsd1)),upr=Inf)+
p*clamp(dnorm(xvals,m2,exp(logsd2)),upr=Inf)))
}
xvals <- x
ff3(1,2,0.1,0.1,4)
mo3 <- mle2(ff3,
start=list(m1=1,m2=2,logsd1=-1,logsd2=-1,xsplit=4),
data=list(xvals=x))
## Coefficients:
## m1 m2 logsd1 logsd2 xsplit
## 3.99915532 12.00242510 -0.09344953 -1.13971551 8.43767997 结果看起来是合理的。
https://stackoverflow.com/questions/21632639
复制相似问题
