迭代平方时间复杂度
迭代平方时间复杂度
提问于 2018-04-28 10:29:52
我有以下迭代平方的实现:
def power(a, b):
result = 1
while b > 0:
if b % 2 == 1:
result = mult(result, a)
a = mult(a, a)
b = b // 2
return resultmult()方法乘以2个给定的数,当一个是x比特的长度,另一个是y位的长度时,乘法所需的运算数是x*y+(x+y)运算,这在复杂性分析中需要考虑。
当a是n位长,b是m位长时,我试图找到一个O()表示法界,当a是n位长,b是m位长时,作为n和m函数完成的广义运算数的界。我只需要考虑乘法线,并检查最坏的情况。
最糟糕的情况是,当b是一个m位数时,所有m二进制数都是1,那么我就有循环的m迭代,在每一次迭代中,if条件都是真的。
我不知道该如何做,我应该如何在计算中考虑到a在每次迭代中都会增长?我如何把它用某种有限和,可能是几何级数,来计算呢?
谢谢
Stack Overflow用户
发布于 2018-04-28 11:12:34
我认为这种算法的复杂性与a无关。
在回顾复杂性时,我认为循环数是由于m而导致的最高复杂度的主要指标。
在b的值中运行,如果b>0时,我们可以看到如下数字:
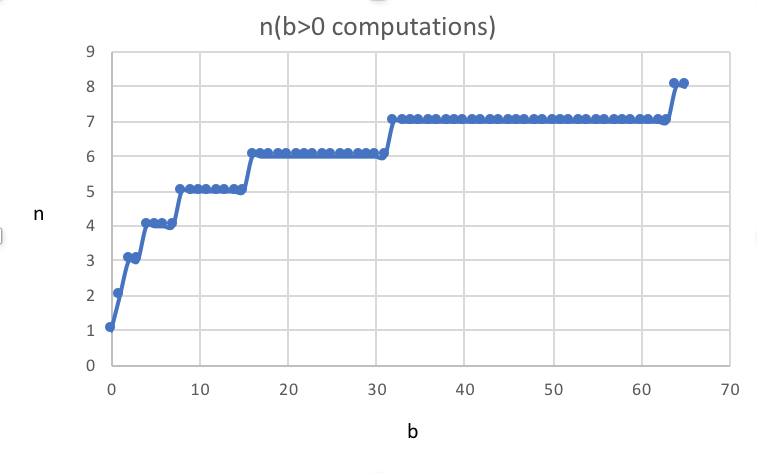
有趣的是,我们看到每个2的倍数(即1,2,4,8,16,32,64)的n个循环的增加。
粗略地说,我认为这个算法的复杂性与O(log2(n))密切相关。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/50075509
复制相关文章
相似问题

