检测两种不同的多边形自交情况(交集发生在内部或外部)
我正在编写一个算法,它将复杂的(自交)多边形分割成一个或多个简单的多边形,以便在我的碰撞检测算法中使用。这可以通过添加/删除顶点和创建新的多边形来完成。
为此,我检测多边形中的所有段交叉口,并将它们按较低的交点x排序,然后按顺序处理每个段交点。但是,有两种类型的交集是可以发生的,我需要根据已经发生的类型对多边形进行不同的拆分。以下是两个可能的案例的说明:
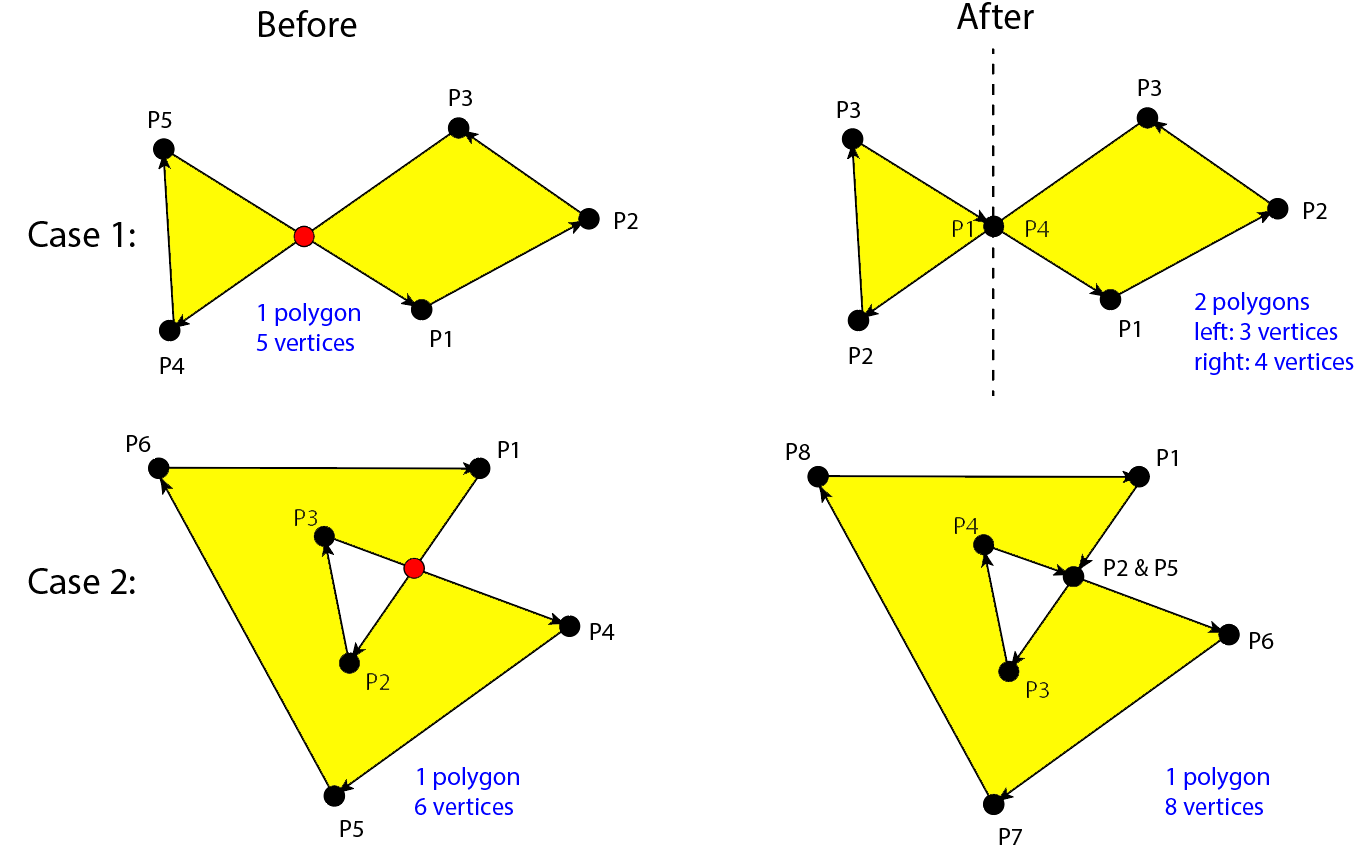
我已经知道如何处理每个交集类型,但我不知道的是如何检测给定的交集是否对应于案例1或案例2。有什么方法可以确定这一点吗?我有算法中所需的所有信息(顶点及其顺序、交集和导致它们的分段,.)。
假设在Q点的段(P_i,P_i+1)和(P_j,P_j+1)与j>i之间有一个交点。
案例1: I将多边形分成两个多边形,Q,P_i+1,…,P_j,Q和Q,P_j+1,…,P_i,Q。
案例2: I在多边形中插入顶点V,得到的多边形是P1,.,P_i,V,P_i+1,.,P_j,Q,P_j+1,.,P1
因此,我所需要的缺失信息是找出由Q,P_i+1,.,P_j形成的循环是“外部”循环(案例1)还是“内部”循环(案例2)。
我读过关于由循环形成的多边形的有符号区域的东西,但是没有完全理解它。我不是在寻找最有效的算法,只是一个能工作的算法。谢谢!
回答 2
Stack Overflow用户
发布于 2019-01-04 16:56:31
如果在交叉口将复杂多边形拆分为简单多边形,则:
- 案例1:简单多边形不重叠
- 案例2:简单多边形重叠,其中一个简单多边形实际上是一个“逆多边形”(描述要排除什么,而不是描述要包含什么)。
这种差异可以通过“在另一个多边形内的一个多边形中的所有顶点或接触另一个多边形中的所有顶点”来确定。
请注意,对于案例2,您可能可以将一个多边形插入另一个多边形中,从而得到一个简单的多边形(例如,对于您的图来说,您将得到"P1、交集、P3、P2、交集、P4、P5、P6")。
然而,你忽略了更多的案例。例如,从第二个图开始(对于第二个例子),将P3向上拖动,使其位于从P6到P1的直线上方(导致在涉及P3的两条边的两边没有多边形)。另一个例子是“图8”,图8中有六个顶点,中间有两个相同的边(可以通过删除中间的两个边转换成一个简单的矩形)。
为了获得更多的乐趣,请考虑这样的事情(但是没有外部圈):
大多数情况下,使它在所有可能的情况下正确工作的机会是零;解决这个问题的唯一明智的办法是预防(找到一种方法来防止需要处理复杂的多边形)。
Stack Overflow用户
发布于 2019-01-05 07:35:40
首先构造多边形的平面直线图 (PSLG)。换句话说,在每个交点处,将多边形看作是一组分段和多个分段。有一种边缘情况是,两个或多个段可以在一个非平凡段中重叠,而不是一个点。在PSLG中,交集段应该是单个的、独立的段,但是我们也需要知道有多少线段与它重叠。因此,这个退化多边形(A-B-C-D-E-F-G-A)
A-C-B-D
| /
| /
G--E---F转成
3
*-*-*-*
| /
| /
*--*---* ,
2省略所有标明1的标签。
下一步是计算这个PSLG的组合嵌入。这意味着我们在顶点上循环,按逆时针顺序按角度对每个顶点的入射边进行排序。在标准的计算几何方式中,我们可以使用有符号区域来获得一个不涉及trig的比较器。
现在,我们有了这样的数据结构。
3
t-u-v-w
| /
| /
x--y---z ,
2
t: t-u, t-x, t-y
u: u-v (3), u-t
v: v-w, v-u (3)
w: w-v, w-y
x: x-y, x-t
y: y-z (2), y-w, y-x
z: z-y (2)我们得到了一个有向边的排列(以后是飞镖),每个边都指向列表中的下一个边(如果需要的话,可以绕一圈)。
t-u -> t-x
t-x -> t-u
u-v (3) -> u-t
u-t -> u-v (3)
v-w -> v-u (3)
v-u (3) -> v-w
w-v -> w-y
w-y -> w-v
x-y -> x-t
x-t -> x-y
y-z (2) -> y-w
y-w -> y-x
y-x -> y-z (2)
z-y (2) -> z-y (2)我们通过构造一个新的排列来计算这种嵌入的对偶,其中每个省道都指向其当前赋值的相反方向。
t-u -> x-t
x-t -> y-x
y-x -> z-y (2)
z-y (2) -> y-z (2)
y-z (2) -> w-y
w-y -> v-w
v-w -> u-v (3)
u-v (3) -> t-u
t-x -> u-t
u-t -> v-u (3)
v-u (3) -> w-v
w-v -> y-w
y-w -> x-y
x-y -> t-x现在,我已经将置换分组为循环。这些循环是PSLG的面(多边形内按顺时针顺序排列,无限面按逆时针顺序排列)。使用一个符号面积测试来找到无限的面。
回到图的表示,首先对根植于无限面的人脸进行深度搜索,将每个面标记为奇数(如果边上的数字之和为奇数)或偶数。奇数周期的集合是您正在寻找的结果。
实际上,现在我已经写出了这个完整的答案,最好是删除开头的偶数多重段,把相邻的多边形一起擦掉。这可能会导致多个无限面,但检测方法仍然有效。
https://stackoverflow.com/questions/54047675
复制相似问题
