基于优化的离散点平滑算法

YoungTimes

发布于 2022-12-12 14:39:31

2.7K0

发布于 2022-12-12 14:39:31

文章被收录于专栏：半杯茶的小酒杯半杯茶的小酒杯

曲线平滑算法是Planning中一种基础算法，在路径优化、速度优化中都有广泛应用。本文主要研究下Apollo中基于优化方法的离散点平滑算法。

先上效果图。如下图所示，绿色线是待平滑的参考线(实际不会有这种参考线，只是为验证下效果)，通过优化平滑算法，可以得到青色的平滑曲线。

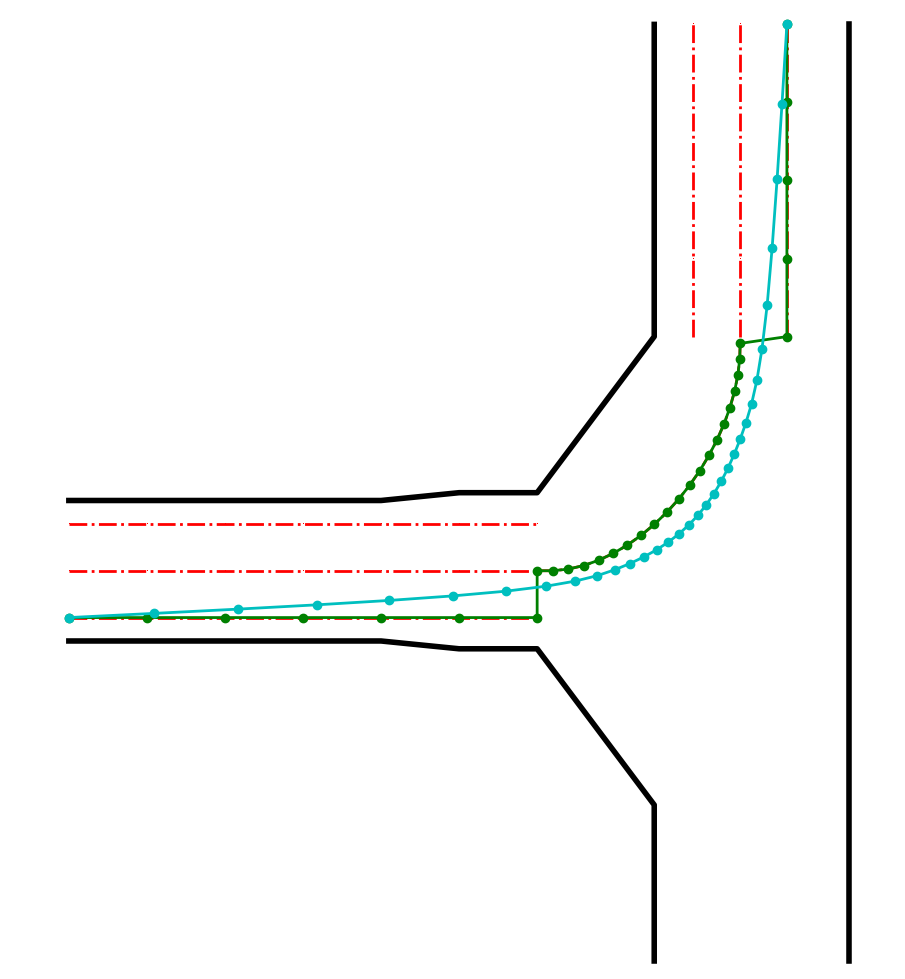
红色线为车道中心线，黑色线为道路边界线

1.离散点曲线平滑的数学原理

如下图所示，P_0 ，P_1 ，P_2 ，P_3 ，…，P_n ，一共n+1个离散点组成原始参考线。

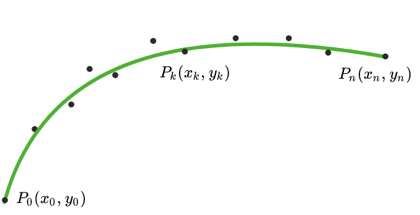
开发者说丨离散点曲线平滑原理中介绍了一种通过对原始参考线上离散点的有限偏移对原始参考线进行平滑的方法，能够将原始参考线(黑色的离散点)转化为平滑的参考线(绿色曲线)。

文中使用的离散点平滑的Cost函数：

\begin{aligned} cost & = \sum_{i=0}^{n - 2}(x_{i} + x_{i + 2} - 2 x_{i + 1})^2 + (y_{i} + y_{i + 2} - 2 y_{i + 1})^2 \\ &= \sum_0^{n - 1} (x_i - x_{i + 1})^2 + (y_i - y_{i + 1})^2 \\ &= \sum_0^{n-1} (x_i - x_{i-ref})^2 + (y_i - y_{i-ref})^2 \end{aligned}

Cost分为三个部分：第一部分为平滑度Cost；第二部分为长度Cost；第三部分为相对原始点偏移Cost。

详细的原理可以参考原文，这里主要实现具体的代码实现。

2.离散点平滑转换为二次规划问题

2.1 平滑性Cost

cost_1 = \sum_{i=0}^{n - 2}(x_{i} + x_{i + 2} - 2 x_{i + 1})^2 + (y_{i} + y_{i + 2} - 2 y_{i + 1})^2

展开上式的x部分：

cost_{1x} = \sum_{i=0}^{n-2} (x_{i}^2 + 4 x_{i + 1}^2 + x_{i + 2}^2 - 4 x_i x_{i + 1} + 2 x_i x_{i+2} - 4 x_{i + 1} x_{i + 2})

以6个点为例,展开上式:

\begin{aligned} cost_{1x} &= x_0^2 + 4x_1^2 + x_2^2 - 4x_0 x_1 + 2x_0 x_2 - 4x_1 x_2 \\ &+ x_1^2 + 4x_2^2 + x_3^2 - 4x_1 x_2 + 2x_1 x_3 - 4x_2 x_3 \\ &+ x_2^2 + 4x_3^2 + x_4^2 - 4x_2 x_3 + 2x_2 x_4 - 4x_3 x_4 \\ &+ x_3^2 + 4x_4^2 + x_5^2 - 4x_3 x_4 + 2x_3 x_5 - 4x_4 x_5 \end{aligned}

转化为二次型的形式：

\frac{1}{2} x^T P x + Q

其中：

P_1= \begin{bmatrix} 1 & -2 & 1 & 0 & 0 & 0 \\ -2 & 5 & -4 & 1 & 0 & 0 \\ 1 & -4 & 6 & -4 & 1 & 0 \\ 0 & 1 & -4 & 6 & -4 & 0 \\ 0 & 0 & 1 & -4 & 5 & -2 \\ 0 & 0 & 0 & 1 & -2 & 1 \\ \end{bmatrix}

x= \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix}

Q_1 = 0

2.2 长度Cost

cost_2= \sum_0^{n - 1} (x_i - x_{i + 1})^2 + (y_i - y_{i + 1})^2

以6个点为例,展开上式的x部分:

\begin{aligned} cost_{2x} &= x_0^2 + x_1^2 - 2 x_0 x_1 \\ &+ x_1^2 + x_2^2 - 2 x_1 x_2 \\ &+ x_2^2 + x_3^2 - 2 x_2 x_3 \\ &+ x_3^2 + x_4^2 - 2 x_3 x_4 \\ &+ x_4^2 + x_5^2 - 2 x_4 x_5 \\ \end{aligned}

转换为二次型形式：

P_2 = \begin{bmatrix} 1 & -1 & 0 & 0 & 0 & 0 \\ -1 & 2 & -1 & 0 & 0 & 0 \\ 0 & -1 & 2 & -1 & 0 & 0 \\ 0 & 0 & -1 & 2 & -1 & 0 \\ 0 & 0 & 0 & -1 & 2 & -1 \\ 0 & 0 & 0 & 0 & -1 & 1 \\ \end{bmatrix}

Q_2 = 0

2.3 偏移Cost

cost_3= \sum_{i=0}^{n} (x_i - x_{i-ref})^2 + (y_i - y_{i-ref})^2

以6个点为例,展开上式的x部分:

\begin{aligned} cost_{3x} &= x_0^2 + x_{ref0}^2 - 2 x_0 x_{ref0} \\ &+ x_1^2 + x_{ref1}^2 - 2 x_1 x_{ref1} \\ &+ x_2^2 + x_{ref2}^2 - 2 x_2 x_{ref2} \\ &+ x_3^2 + x_{ref3}^2 - 2 x_3 x_{ref3} \\ &+ x_4^2 + x_{ref4}^2 - 2 x_4 x_{ref4} \\ &+ x_5^2 + x_{ref5}^2 - 2 x_5 x_{ref5} \\ \end{aligned}

转换为二次型形式：

P_3= \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}

Q_3= \begin{bmatrix} -2 x_{ref_0} \\ -2 x_{ref_1} \\ -2 x_{ref_2} \\ -2 x_{ref_3} \\ -2 x_{ref_4} \\ -2 x_{ref_5} \\ \end{bmatrix}

2.4 计算P矩阵

cost = w_1 cost_1 + w_2 * cost_2 + w_3 * cost_3

因此P矩阵就是把

P_1

、

P_2

、

P_3

三个矩阵加起来，同时增加曲率slack。

\begin{bmatrix} X+Y+Z & -2X-Y & X & 0 & 0 & 0 & \cdots \\ 0 & 5X+2Y+Z & -4X-Y & X & 0 & 0 & \cdots \\ 0 & 0 & 6X+2Y+Z & -4X-Y & X & 0 & \cdots \\ 0 & 0 & 0 & 6X+2Y+Z & -4X-Y & X & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots \\ 0 & 0 & 0 & 0 & 5X+2Y+Z & -2X-Y & \cdots \\ 0 & 0 & 0 & 0 & 0 & X+Y+Z & \cdots \\ 0 & 0 & 0 & 0 & 0 & 0 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots \\ 0 & 0 & 0 & 0 & 0 & 0 & \cdots \\ \end{bmatrix}

其中：

X = w_1 \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}

Y = w_2 \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}

Z = w_3 \times \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}

2.5 计算Q矩阵

同P矩阵一样，Q矩阵也是把三部分加起来。

Q = \begin{bmatrix} -2 w_3 x_{ref_0} \\ -2 w_3 y_{ref_0} \\ -2 w_3 x_{ref_1} \\ -2 w_3 y_{ref_1} \\ -2 w_3 x_{ref_2} \\ -2 w_3 y_{ref_2} \\ \vdots \\ -2 w_3 x_{ref_n} \\ -2 w_3 y_{ref_n} \\ slack_{w1} \\ \vdots \\ slack_{w_{n-2}} \\ \end{bmatrix}

2.6 计算待优化变量

x = \begin{bmatrix} x_0 \\ y_0 \\ x_1 \\ y_1 \\ x_2 \\ y_2 \\ ... \\ x_n \\ y_n \\ slack_0 \\ \vdots \\ slack_{n-2} \\ \end{bmatrix}

2.7 约束条件

2.7.1 范围约束

优化时，现在坐标在一定范围内变化。

l_{bound} \leq x_i - x_{ref_i} \leq u_{bound}

l_{bound} \leq y_i - y_{ref_i} \leq u_{bound}

其中，

i=0, 1, ..., n

将约束转换为

LB \leq Ax \leq UB

的形式, A是一个单位矩阵。

A = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ \end{bmatrix}

约束bound:

x_{ref_i} + l_{bound} \leq x_i \leq x_{ref_i} + u_{bound}

y_{ref_i} + l_{bound} \leq y_i \leq y_{ref_i} + u_{bound}

其中，

i=0, 1, ..., n

2.7.2 曲率约束

原始的约束方程:

(x_i + x_{i+2} - x_{i+1})^2 + (y_i + y_{i+2} - y_{i+1})^2 - slack_{i} \leq (\Delta s^2 cur_{cstr})^2

其中,

i = 0, 1, ..., n - 2

线性化的曲率约束方程：

F^{\prime}({x_{ref}}) X \leq (\Delta s^2 \times cur_{cstr})^2 -F(x_{ref}) + F^{\prime}(x_{ref}) x_{ref}

其中：

\begin{aligned} F^{\prime}(x_{ref}) &= \begin{bmatrix} \frac{\partial F}{\partial x_{i-1}} \\ \frac{\partial F}{\partial y_{i-1}} \\ \frac{\partial F}{\partial x_{i}} \\ \frac{\partial F}{\partial y_{i}} \\ \frac{\partial F}{\partial x_{i+1}} \\ \frac{\partial F}{\partial y_{i+1}} \\ \end{bmatrix} \\ & = \begin{bmatrix} 2(x_{i - 1} + x_{i + 1} - 2 x_i) \\ 2(y_{i - 1} + y_{i + 1} - 2 y_i) \\ -4(x_{i - 1} + x_{i + 1} - 2 x_i) \\ -4(y_{i - 1} + y_{i + 1} - 2 y_i) \\ 2(x_{i - 1} + x_{i + 1} - 2 x_i) \\ 2(y_{i - 1} + y_{i + 1} - 2 y_i) \\ \end{bmatrix} \end{aligned}

转换成矩阵形式：

A = \begin{bmatrix} \frac{\partial F}{\partial x_{0}} & \frac{\partial F}{\partial y_{0}} & \frac{\partial F}{\partial x_{1}} & \frac{\partial F}{\partial y_{1}} & \frac{\partial F}{\partial x_{2}} & \frac{\partial F}{\partial y_{2}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0\\ 0 & 0 & \frac{\partial F}{\partial x_{1}} & \frac{\partial F}{\partial y_{1}} & \frac{\partial F}{\partial x_{2}} & \frac{\partial F}{\partial y_{3}} & \frac{\partial F}{\partial x_{3}} & \frac{\partial F}{\partial y_{3}} & 0 & 0 & 0 & 0 & 0 & 0& \cdots & 0 & 0\\ 0 & 0 & 0 & 0 & \frac{\partial F}{\partial x_{2}} & \frac{\partial F}{\partial y_{2}} & \frac{\partial F}{\partial x_{3}} & \frac{\partial F}{\partial y_{3}} & \frac{\partial F}{\partial x_{4}} & \frac{\partial F}{\partial y_{4}} & 0 & 0 & 0 & 0& \cdots & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & \frac{\partial F}{\partial x_{3}} & \frac{\partial F}{\partial y_{3}} & \frac{\partial F}{\partial x_{4}} & \frac{\partial F}{\partial y_{4}} & \frac{\partial F}{\partial x_{5}} & \frac{\partial F}{\partial y_{5}} & 0 & 0 & \cdots & 0 & 0\\ \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots & \ddots &\vdots &\vdots \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{\partial F}{\partial x_{n-2}} & \frac{\partial F}{\partial y_{n-2}} & \frac{\partial F}{\partial x_{n-1}} & \frac{\partial F}{\partial y_{n-1}} & \frac{\partial F}{\partial x_{n}} & \frac{\partial F}{\partial y_{n}}\\ \end{bmatrix}

3. 代码实现

3.1 待优化变量

待优化变量包括n个坐标和n-2个slack,因此共有2 * n + (n-2)个待优化变量。

  num_of_points_ = static_cast<int>(ref_points_.size());
  num_of_pos_variables_ = num_of_points_ * 2;
  num_of_slack_variables_ = num_of_points_ - 2;
  num_of_variables_ = num_of_pos_variables_ + num_of_slack_variables_;

  num_of_variable_constraints_ = num_of_variables_;
  num_of_curvature_constraints_ = num_of_points_ - 2;
  num_of_constraints_ =
      num_of_variable_constraints_ + num_of_curvature_constraints_;

3.2 P矩阵(Kernel)

根据数值的规律，P矩阵有数值区域可以分为五个部分：第1、2列；第3、4列；倒数第1、2列；倒数第3、4列；中间所有列；

第1、2列：X + Y + Z；之所以有两列，是因为坐标有x和y两个变量。

  std::vector<std::vector<std::pair<c_int, c_float>>> columns;
  columns.resize(num_of_variables_);

  for (int col = 0; col < 2; ++col) {
    columns[col].emplace_back(col, weight_fem_pos_deviation_ +
                                       weight_path_length_ +
                                       weight_ref_deviation_);
    ++col_num;
  }

第3、4列：-2X-Y & 5X + 2Y + Z；

  for (int col = 2; col < 4; ++col) {
    columns[col].emplace_back(
        col - 2, -2.0 * weight_fem_pos_deviation_ - weight_path_length_);
    columns[col].emplace_back(col, 5.0 * weight_fem_pos_deviation_ +
                                       2.0 * weight_path_length_ +
                                       weight_ref_deviation_);
    ++col_num;
  }

第5列~第num_of_points_-2列: X & -4X -Y & 6X + 2Y + Z；

  int second_point_from_last_index = num_of_points_ - 2;
  for (int point_index = 2; point_index < second_point_from_last_index;
       ++point_index) {
    int col_index = point_index * 2;
    for (int col = 0; col < 2; ++col) {
      col_index += col;
      columns[col_index].emplace_back(col_index - 4, weight_fem_pos_deviation_);
      columns[col_index].emplace_back(
          col_index - 2,
          -4.0 * weight_fem_pos_deviation_ - weight_path_length_);
      columns[col_index].emplace_back(
          col_index, 6.0 * weight_fem_pos_deviation_ +
                         2.0 * weight_path_length_ + weight_ref_deviation_);
      ++col_num;
    }
  }

倒数第3、4列：-2X-Y & 5X + 2Y + Z；

  int second_point_col_from_last_col = num_of_pos_variables_ - 4;
  int last_point_col_from_last_col = num_of_pos_variables_ - 2;
  for (int col = second_point_col_from_last_col;
       col < last_point_col_from_last_col; ++col) {
    columns[col].emplace_back(col - 4, weight_fem_pos_deviation_);
    columns[col].emplace_back(
        col - 2, -4.0 * weight_fem_pos_deviation_ - weight_path_length_);
    columns[col].emplace_back(col, 5.0 * weight_fem_pos_deviation_ +
                                       2.0 * weight_path_length_ +
                                       weight_ref_deviation_);
    ++col_num;
  }

倒数第1、2列：X + Y + Z；

  for (int col = last_point_col_from_last_col; col < num_of_pos_variables_;
       ++col) {
    columns[col].emplace_back(col - 4, weight_fem_pos_deviation_);
    columns[col].emplace_back(
        col - 2, -2.0 * weight_fem_pos_deviation_ - weight_path_length_);
    columns[col].emplace_back(col, weight_fem_pos_deviation_ +
                                       weight_path_length_ +
                                       weight_ref_deviation_);
    ++col_num;
  }

3.3 CSC矩阵处理

CSC是按列存储稀疏矩阵，稍微有点复杂，简单复习一下。

>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]])

其中indptr中的数据代表矩阵中每一列所存储数据在data中的开始和结束的索引。例如，这里indptr为[0, 2, 3, 6]，即表示在data中，索引[0,2)为第一列的数据，索引[2, 3)为第二列的数据，索引[3, 6)为第三列的数据；indices中数据代表对应的data中的数据在其所在列中的所在行数，例如，这里的indices为[0, 2, 2, 0, 1, 2]，表示在data中，数据1在第0行，数据2在第2行，数据3在第2行，数据4在第0行，数据5在1行，数据6在第6行。

  int ind_p = 0;
  for (int i = 0; i < num_of_variables_; ++i) {
    P_indptr->push_back(ind_p);
    for (const auto& row_data_pair : columns[i]) {
      // Rescale by 2.0 as the quadratic term in osqp default qp problem setup
      // is set as (1/2) * x' * P * x
      P_data->push_back(row_data_pair.second * 2.0);
      P_indices->push_back(row_data_pair.first);
      ++ind_p;
    }
  }
  P_indptr->push_back(ind_p);

3.4 Q矩阵

void FemPosDeviationOsqpInterface::CalculateOffset(std::vector<c_float>* q) {
  for (int i = 0; i < num_of_points_; ++i) {
    const auto& ref_point_xy = ref_points_[i];
    q->push_back(-2.0 * weight_ref_deviation_ * ref_point_xy.first);
    q->push_back(-2.0 * weight_ref_deviation_ * ref_point_xy.second);
  }
  for (int i = 0; i < num_of_slack_variables_; ++i) {
    (*q)[num_of_pos_variables_ + i] = weight_curvature_constraint_slack_var_;
  }
}

3.5 约束条件

3.5.1 范围约束

构造A矩阵。

  int ind_A = 0;
  for (int i = 0; i < num_of_variables_; ++i) {
    A_data->push_back(1.0);
    A_indices->push_back(i);
    A_indptr->push_back(ind_A);
    ++ind_A;
  }
  A_indptr->push_back(ind_A);

构造LB和UB。

  lower_bounds->resize(num_of_constraints_);
  upper_bounds->resize(num_of_constraints_);

  for (int i = 0; i < num_of_points_; ++i) {
    const auto& ref_point_xy = ref_points_[i];
    (*upper_bounds)[i * 2] = ref_point_xy.first + bounds_around_refs_[i];
    (*upper_bounds)[i * 2 + 1] = ref_point_xy.second + bounds_around_refs_[i];
    (*lower_bounds)[i * 2] = ref_point_xy.first - bounds_around_refs_[i];
    (*lower_bounds)[i * 2 + 1] = ref_point_xy.second - bounds_around_refs_[i];
  }

  for (int i = 0; i < num_of_slack_variables_; ++i) {
    (*upper_bounds)[num_of_pos_variables_ + i] = 1e20;
    (*lower_bounds)[num_of_pos_variables_ + i] = 0.0;
  }

3.5.2 曲率约束

计算A矩阵。

  const double scale_factor = 1;

  std::vector<std::vector<double>> lin_cache;
  for (int i = 1; i < num_of_points_ - 1; ++i) {
    lin_cache.push_back(CalculateLinearizedFemPosParams(points, i));
  }

  std::vector<std::vector<std::pair<c_int, c_float>>> columns;
  columns.resize(num_of_variables_);

  for (int i = 0; i < num_of_variables_; ++i) {
    columns[i].emplace_back(i, 1.0);
  }

  for (int i = num_of_pos_variables_; i < num_of_variables_; ++i) {
    columns[i].emplace_back(i + num_of_slack_variables_, -1.0 * scale_factor);
  }

  for (int i = 2; i < num_of_points_; ++i) {
    int index = 2 * i;
    columns[index].emplace_back(i - 2 + num_of_variables_,
                                lin_cache[i - 2][4] * scale_factor);
    columns[index + 1].emplace_back(i - 2 + num_of_variables_,
                                    lin_cache[i - 2][5] * scale_factor);
  }

  for (int i = 1; i < num_of_points_ - 1; ++i) {
    int index = 2 * i;
    columns[index].emplace_back(i - 1 + num_of_variables_,
                                lin_cache[i - 1][2] * scale_factor);
    columns[index + 1].emplace_back(i - 1 + num_of_variables_,
                                    lin_cache[i - 1][3] * scale_factor);
  }

  for (int i = 0; i < num_of_points_ - 2; ++i) {
    int index = 2 * i;
    columns[index].emplace_back(i + num_of_variables_,
                                lin_cache[i][0] * scale_factor);
    columns[index + 1].emplace_back(i + num_of_variables_,
                                    lin_cache[i][1] * scale_factor);
  }

  int ind_a = 0;
  for (int i = 0; i < num_of_variables_; ++i) {
    A_indptr->push_back(ind_a);
    for (const auto& row_data_pair : columns[i]) {
      A_data->push_back(row_data_pair.second);
      A_indices->push_back(row_data_pair.first);
      ++ind_a;
    }
  }
  A_indptr->push_back(ind_a);

计算曲率约束：

-1e20 \leq F^{\prime}({x_{ref}}) X \leq (\Delta s^2 \times cur_{cstr})^2 -F(x_{ref}) + F^{\prime}(x_{ref}) x_{ref}

  double interval_sqr = average_interval_length_ * average_interval_length_;
  double curvature_constraint_sqr = (interval_sqr * curvature_constraint_) *
                                    (interval_sqr * curvature_constraint_);
  for (int i = 0; i < num_of_curvature_constraints_; ++i) {
    (*upper_bounds)[num_of_variable_constraints_ + i] =
        (curvature_constraint_sqr - lin_cache[i][6]) * scale_factor;
    (*lower_bounds)[num_of_variable_constraints_ + i] = -1e20;
  }

3.6 OSQP优化求解

Kernel 和约束都准备好之后，调用OSQP进行优化求解。

  OSQPSettings* settings =
      reinterpret_cast<OSQPSettings*>(c_malloc(sizeof(OSQPSettings)));
  osqp_set_default_settings(settings);
  settings->max_iter = max_iter_;
  settings->time_limit = time_limit_;
  settings->verbose = verbose_;
  settings->scaled_termination = scaled_termination_;
  settings->warm_start = warm_start_;
  settings->polish = true;
  settings->eps_abs = 1e-5;
  settings->eps_rel = 1e-5;
  settings->eps_prim_inf = 1e-5;
  settings->eps_dual_inf = 1e-5;

  // Define osqp workspace
  OSQPWorkspace* work = nullptr;
  osqp_setup(&work, data, settings);
  // work = osqp_setup(data, settings);

  // Initial solution 
  OptimizeWithOsqp(primal_warm_start, &work);

经过优化求解之后，就得到了文章开头的平滑曲线。

附一：OSQP安装

源码下载路径

https://github.com/osqp/osqp/releases/tag/v0.6.2，选择complete_sources.*下载。

代码编译安装

mkdir build

cd build

cmake -D CMAKE_INSTALL_PREFIX=~/code/OSQP/osqp/output ..

make

make install

参考材料

1、https://www.cnblogs.com/icathianrain/p/14407757.html

2、https://github.com/ApolloAuto/apollo/tree/master/modules/planning/math/discretized_points_smoothing

本文参与腾讯云自媒体分享计划，分享自微信公众号。

原始发表：2022-07-16，如有侵权请联系 cloudcommunity@tencent.com 删除

https

网络安全

编程算法

本文分享自半杯茶的小酒杯微信公众号，前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体分享计划，欢迎热爱写作的你一起参与！

https

网络安全

编程算法

登录后参与评论

0 条评论

热度