前往小程序，Get更优阅读体验！
立即前往
文档建议反馈控制台
首页
学习
活动
专区
工具
TVP
最新优惠活动
文章/答案/技术大牛
发布
首页
学习
活动
专区
工具
TVP最新优惠活动
返回腾讯云官网
社区首页 >专栏 >【数据挖掘】K-Means 二维数据聚类分析 ( K-Means 迭代总结 | K-Means 初始中心点选择方案 | K-Means 算法优缺点 | K-Means 算法变种 )

【数据挖掘】K-Means 二维数据聚类分析 ( K-Means 迭代总结 | K-Means 初始中心点选择方案 | K-Means 算法优缺点 | K-Means 算法变种 )

作者头像
韩曙亮
发布于 2023-03-27 19:54:16
6610
发布于 2023-03-27 19:54:16
举报
文章被收录于专栏：韩曙亮的移动开发专栏韩曙亮的移动开发专栏

文章目

K-Means 二维数据 聚类分析 数据样本及聚类要求

数据样本及聚类要求 :

① 数据样本 : 数据集样本为

6

个点 ,

A_1 ( 2 , 4 )

,

A_2 ( 3 , 7 )

,

B_1 ( 5 , 8 )

,

B_2 ( 9 , 5 )

,

C_1 ( 6 , 2 )

,

C_2 ( 4 , 9 )

;

② 聚类个数 : 分为

3

个聚类 ;

③ 距离计算方式 : 使用 曼哈顿距离 , 计算样本之间的相似度 ; 曼哈顿距离的计算方式是 两个维度的数据差 的 绝对值 相加 ;

④ 中心点初始值 : 选取

A_1 , B_1 , C_1

三个样本为聚类的初始值 , 这是实点 ; 如果选取非样本的点作为初始值 , 就是虚点 ;

⑤ 要求 : 使用 K-Means 算法迭代

2

次 ;

⑥ 中心值精度 : 计算过程中中心值小数向下取整 ;

二维数据曼哈顿距离计算

1 . 曼哈顿距离 公式如下 :

d(i, j) = | x_{i1} - x_{j1} | + | x_{i2} - x_{j2} | + \cdots + | x_{ip} - x_{jp} |
d(i, j)

表示两个样本之间的距离 , 曼哈顿距离 ;

p

表示属性的个数 , 每个样本有

p

个属性 ;

i

和

j

表示两个 样本的索引值 , 取值范围是

\{1 , 2, \cdots , q\}

;

x_{ip} - x_{jp}

表示两个样本 第

p

个属性值 的差值 ,

x_{i1} - x_{j1}

表示两个样本 第

1

个属性值 的差值 ,

x_{i2} - x_{j2}

表示两个样本 第

2

个属性值 的差值 ;

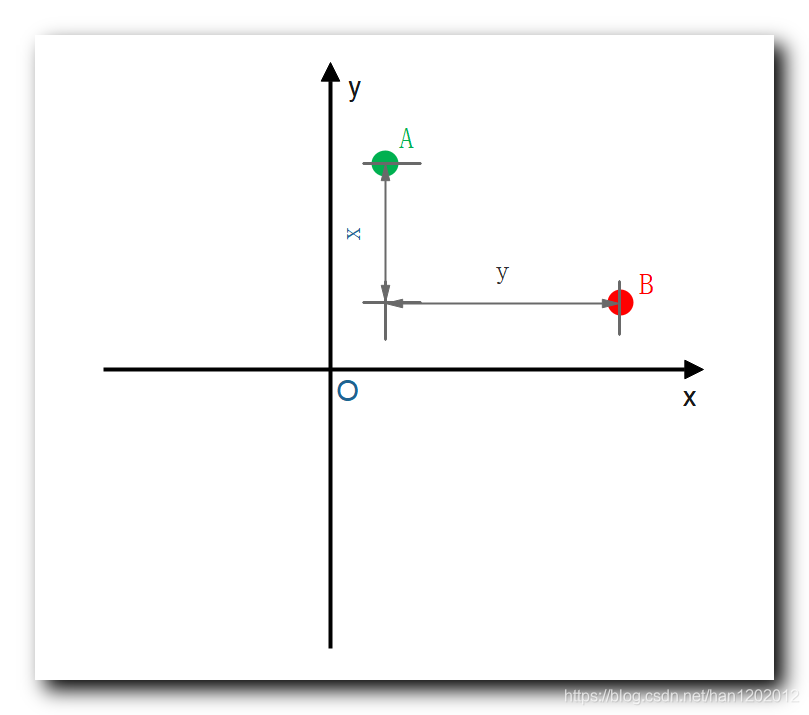
2 . 曼哈顿距离图示 : 曼哈顿的街道都是横平竖直的 , 从

A

点到

B

点 , 一般就是其

x

轴坐标差 加上其

y

轴坐标差 , 即

x + y

;

在这里插入图片描述
在这里插入图片描述

3 . 本题目中的样本距离计算示例 : 两个样本的曼哈顿距离是

x

属性差的绝对值 , 加上

y

属性差的绝对值 , 之和 ;

计算

A_1 ( 2 , 4 )

,

A_2 ( 3 , 7 )

的距离 :

d(A_1 , A_2) = | 2 - 3 | + |4 - 7| = 4
A_1

样本与

A_2

样本之间的距离是

4

;

K-Means 算法 步骤

K-Means 算法 步骤 : 给定数据集

X

, 该数据集有

n

个样本 , 将其分成

K

个聚类 ;

① 中心点初始化 : 为

K

个聚类分组选择初始的中心点 , 这些中心点称为 Means ; 可以依据经验 , 也可以随意选择 ;

② 计算距离 : 计算

n

个对象与

K

个中心点 的距离 ; ( 共计算

n \times K

次 )

③ 聚类分组 : 每个对象与

K

个中心点的值已计算出 , 将每个对象分配给距离其最近的中心点对应的聚类 ;

④ 计算中心点 : 根据聚类分组中的样本 , 计算每个聚类的中心点 ;

⑤ 迭代直至收敛 : 迭代执行 ② ③ ④ 步骤 , 直到 聚类算法收敛 , 即 中心点 和 分组 经过多少次迭代都不再改变 , 也就是本次计算的中心点与上一次的中心点一样 ;

第一次迭代 : 步骤 ( 1 ) 中心点初始化

初始化中心点 :

3

个聚类的中心点 , 在题目中已经给出 ;

① 聚类

1

中心点 :

A_1 ( 2 , 4 )

;

② 聚类

2

中心点 :

B_1 ( 5 , 8 )

;

③ 聚类

3

中心点 :

C_1 ( 6 , 2 )

;

第一次迭代 : 步骤 ( 2 ) 计算距离

距离计算次数 : 这里需要计算所有的样本 , 与所有的中心点的距离 , 每个样本都需要计算与

3

个中心点的距离 , 共需要计算

6 \times 3 = 18

次 ;

数据样本 :

A_1 ( 2 , 4 )

,

A_2 ( 3 , 7 )

,

B_1 ( 5 , 8 )

,

B_2 ( 9 , 5 )

,

C_1 ( 6 , 2 )

,

C_2 ( 4 , 9 )

1 . 计算

A_1 ( 2 , 4 )

与 三个中心点

\{ A_1 , B_1 , C_1 \}

之间的距离 :

①

A_1 ( 2 , 4 )

与

A_1 ( 2 , 4 )

的距离 : ( 最小 )

d(A_1 , A_1) = | 2-2 | + | 4-4 | = 0

②

A_1 ( 2 , 4 )

与

B_1 ( 5 , 8 )

的距离 :

d(A_1 , B_1) = | 2-5 | + | 4-8 | = 7

③

A_1 ( 2 , 4 )

与

C_1 ( 6 , 2 )

的距离 :

d(A_1 , C_1) = | 2-6 | + | 4-2 | = 6
A_1 ( 2 , 4 )

与

A_1 ( 2 , 4 )

的距离最小 ;

2 . 计算

A_2 ( 3 , 7 )

与 三个中心点

\{ A_1 , B_1 , C_1 \}

之间的距离 :

①

A_2 ( 3 , 7 )

与

A_1 ( 2 , 4 )

的距离 :

d(A_2 , A_1) = | 3-2 | + | 7-4 | = 4

②

A_2 ( 3 , 7 )

与

B_1 ( 5 , 8 )

的距离 : ( 最小 )

d(A_2 , B_1) = | 3-5 | + | 7-8 | = 3

③

A_2 ( 3 , 7 )

与

C_1 ( 6 , 2 )

的距离 :

d(A_2 , C_1) = | 3-6 | + | 7-2 | = 8
A_2 ( 3 , 7 )

与

B_1 ( 5 , 8 )

的距离最小 ;

3 . 计算

B_1 ( 5 , 8 )

与 三个中心点

\{ A_1 , B_1 , C_1 \}

之间的距离 :

①

B_1 ( 5 , 8 )

与

A_1 ( 2 , 4 )

的距离 :

d(B_1 , A_1) = | 5 -2 | + | 8 -4 | = 7

②

B_1 ( 5 , 8 )

与

B_1 ( 5 , 8 )

的距离 : ( 最小 )

d(B_1 , B_1) = | 5 -5 | + | 8 -8 | = 0

③

B_1 ( 5 , 8 )

与

C_1 ( 6 , 2 )

的距离 :

d(B_1 , C_1) = | 5 -6 | + | 8 -2 | = 7
B_1 ( 5 , 8 )

与

B_1 ( 5 , 8 )

的距离最小 ;

4 . 计算

B_2 ( 9 , 5 )

与 三个中心点

\{ A_1 , B_1 , C_1 \}

之间的距离 :

①

B_2 ( 9 , 5 )

与

A_1 ( 2 , 4 )

的距离 :

d(B_2 , A_1) = | 9 -2 | + | 5 -4 | = 8

②

B_2 ( 9 , 5 )

与

B_1 ( 5 , 8 )

的距离 :

d(B_2 , B_1) = | 9 -5 | + | 5 -8 | = 7

③

B_2 ( 9 , 5 )

与

C_1 ( 6 , 2 )

的距离 : ( 最小 )

d(B_2 , C_1) = | 9 -6 | + | 5 -2 | = 6
B_2 ( 9 , 5 )

与

C_1 ( 6 , 2 )

的距离最小 ;

5 . 计算

C_1 ( 6 , 2 )

与 三个中心点

\{ A_1 , B_1 , C_1 \}

之间的距离 :

①

C_1 ( 6 , 2 )

与

A_1 ( 2 , 4 )

的距离 :

d(C_1 , A_1) = | 6 -2 | + | 2 -4 | = 6

②

C_1 ( 6 , 2 )

与

B_1 ( 5 , 8 )

的距离 :

d(C_1 , B_1) = | 6 -5 | + | 2 -8 | = 7

③

C_1 ( 6 , 2 )

与

C_1 ( 6 , 2 )

的距离 : ( 最小 )

d(C_1 , C_1) = | 6 -6 | + | 2 -2 | = 0
C_1 ( 6 , 2 )

与

C_1 ( 6 , 2 )

的距离最小 ;

6 . 计算

C_2 ( 4 , 9 )

与 三个中心点

\{ A_1 , B_1 , C_1 \}

之间的距离 :

①

C_2 ( 4 , 9 )

与

A_1 ( 2 , 4 )

的距离 :

d(C_2 , A_1) = | 4 -2 | + | 9 -4 | = 7

②

C_2 ( 4 , 9 )

与

B_1 ( 5 , 8 )

的距离 : ( 最小 )

d(C_2 , B_1) = | 4 -5 | + | 9 -8 | = 2

③

C_2 ( 4 , 9 )

与

C_1 ( 6 , 2 )

的距离 :

d(C_2 , C_1) = | 4 -6 | + | 9 -2 | = 9
C_2 ( 4 , 9 )

与

B_1 ( 5 , 8 )

的距离最小 ;

8 . 生成距离表格 : 将上面计算的内容总结到如下表格中 ;

A 1 ( 2 , 4 ) A_1 ( 2 , 4 ) A1​(2,4)

A 2 ( 3 , 7 ) A_2 ( 3 , 7 ) A2​(3,7)

B 1 ( 5 , 8 ) B_1 ( 5 , 8 ) B1​(5,8)

B 2 ( 9 , 5 ) B_2 ( 9 , 5 ) B2​(9,5)

C 1 ( 6 , 2 ) C_1 ( 6 , 2 ) C1​(6,2)

C 2 ( 4 , 9 ) C_2 ( 4 , 9 ) C2​(4,9)

A 1 ( 2 , 4 ) A_1 ( 2 , 4 ) A1​(2,4)

0 0 0

4 4 4

7 7 7

8 8 8

6 6 6

7 7 7

B 1 ( 5 , 8 ) B_1 ( 5 , 8 ) B1​(5,8)

7 7 7

3 3 3

0 0 0

7 7 7

7 7 7

2 2 2

C 1 ( 6 , 2 ) C_1 ( 6 , 2 ) C1​(6,2)

6 6 6

8 8 8

7 7 7

6 6 6

0 0 0

9 9 9

A_1 ( 2 , 4 )
A_2 ( 3 , 7 )
B_1 ( 5 , 8 )
B_2 ( 9 , 5 )
C_1 ( 6 , 2 )
C_2 ( 4 , 9 )
A_1 ( 2 , 4 )
0
4
7
8
6
7
B_1 ( 5 , 8 )
7
3
0
7
7
2
C_1 ( 6 , 2 )
6
8
7
6
0
9
第一次迭代 : 步骤 ( 3 ) 聚类分组

1 . 聚类分组 : 根据计算出的 , 每个样本与

3

个中心点的距离 , 将样本划分到 距离该样本最近的中心点 对应的分组中 ;

A 1 ( 2 , 4 ) A_1 ( 2 , 4 ) A1​(2,4)

A 2 ( 3 , 7 ) A_2 ( 3 , 7 ) A2​(3,7)

B 1 ( 5 , 8 ) B_1 ( 5 , 8 ) B1​(5,8)

B 2 ( 9 , 5 ) B_2 ( 9 , 5 ) B2​(9,5)

C 1 ( 6 , 2 ) C_1 ( 6 , 2 ) C1​(6,2)

C 2 ( 4 , 9 ) C_2 ( 4 , 9 ) C2​(4,9)

A 1 ( 2 , 4 ) A_1 ( 2 , 4 ) A1​(2,4)

0 0 0

4 4 4

7 7 7

8 8 8

6 6 6

7 7 7

B 1 ( 5 , 8 ) B_1 ( 5 , 8 ) B1​(5,8)

7 7 7

3 3 3

0 0 0

7 7 7

7 7 7

2 2 2

C 1 ( 6 , 2 ) C_1 ( 6 , 2 ) C1​(6,2)

6 6 6

8 8 8

7 7 7

6 6 6

0 0 0

9 9 9

A_1 ( 2 , 4 )
A_2 ( 3 , 7 )
B_1 ( 5 , 8 )
B_2 ( 9 , 5 )
C_1 ( 6 , 2 )
C_2 ( 4 , 9 )
A_1 ( 2 , 4 )
0
4
7
8
6
7
B_1 ( 5 , 8 )
7
3
0
7
7
2
C_1 ( 6 , 2 )
6
8
7
6
0
9

2 . 根据表格中的距离 , 为每个样本分组 :

①

A_1 ( 2 , 4 )

距离

A_1 ( 2 , 4 )

中心点最近 , 划分到 聚类

1

中 ;

②

A_2 ( 3 , 7 )

距离

B_1 ( 5 , 8 )

中心点最近 , 划分到 聚类

2

中 ;

③

B_1 ( 5 , 8 )

距离

B_1 ( 5 , 8 )

中心点最近 , 划分到 聚类

2

中 ;

④

B_2 ( 9 , 5 )

距离

C_1 ( 6 , 2 )

中心点最近 , 划分到 聚类

3

中 ;

⑤

C_1 ( 6 , 2 )

距离

C_1 ( 6 , 2 )

中心点最近 , 划分到 聚类

3

中 ;

⑥

C_2 ( 4 , 9 )

距离

B_1 ( 5 , 8 )

中心点最近 , 划分到 聚类

2

中 ;

3 . 最终的聚类分组为 :

① 聚类

1

:

\{ A_1 \}

② 聚类

2

:

\{ A_2 , B_1 , C_2 \}

③ 聚类

3

:

\{ B_2 , C_1 \}
第二次迭代 : 步骤 ( 1 ) 中心点初始化
A_1 ( 2 , 4 )

,

A_2 ( 3 , 7 )

,

B_1 ( 5 , 8 )

,

B_2 ( 9 , 5 )

,

C_1 ( 6 , 2 )

,

C_2 ( 4 , 9 )

1 . 聚类

1

中心点计算 : 计算

\{ A_1 ( 2 , 4 ) \}

中心点

聚类 1 中心点 = ( 2 , 4 )

2 . 聚类

2

中心点计算 : 计算

\{ A_2 ( 3 , 7 ) , B_1 ( 5 , 8 ) , C_2( 4 , 9 ) \}

中心点

聚类 2 中心点 = ( \frac{3 + 5 + 4}{3} , \frac{7 + 8 + 9}{3}) = ( 4 , 8 )

3 . 聚类

3

中心点计算 : 计算

\{ B_2( 9 , 5 ) , C_1 ( 6 , 2 ) \}

中心点

聚类 3 中心点 = ( \frac{9 + 6 }{2} , \frac{5 + 2}{2}) = ( 7 , 3 )
第二次迭代 : 步骤 ( 2 ) 计算距离

计算

6

个点 , 到

3

个中心点的距离 ,

3

个中心点分别是

\{ ( 2 , 4 ) , ( 4 , 8 ) , ( 7 , 3 ) \}

, 直接将两个点的曼哈顿距离填在对应的表格中 ;

如 : 第

1

行 , 第

2

列 :

A_1 ( 2 , 4 )

样本 与

( 4 , 8 )

聚类

2

中心点的 曼哈顿距离 是

6

, 计算过程如下 :

A_1 ( 2 , 4 ) 与 ( 4 , 8 ) 两点曼哈顿距离 = | 2 - 4 | + | 4 - 8 | = 6

A 1 ( 2 , 4 ) A_1 ( 2 , 4 ) A1​(2,4)

A 2 ( 3 , 7 ) A_2 ( 3 , 7 ) A2​(3,7)

B 1 ( 5 , 8 ) B_1 ( 5 , 8 ) B1​(5,8)

B 2 ( 9 , 5 ) B_2 ( 9 , 5 ) B2​(9,5)

C 1 ( 6 , 2 ) C_1 ( 6 , 2 ) C1​(6,2)

C 2 ( 4 , 9 ) C_2 ( 4 , 9 ) C2​(4,9)

( 2 , 4 ) ( 2 , 4 ) (2,4)

0 0 0

4 4 4

7 7 7

8 8 8

6 6 6

7 7 7

( 4 , 8 ) ( 4 , 8 ) (4,8)

6 6 6

2 2 2

1 1 1

8 8 8

8 8 8

1 1 1

( 7 , 3 ) ( 7 , 3 ) (7,3)

6 6 6

8 8 8

7 7 7

4 4 4

2 2 2

9 9 9

A_1 ( 2 , 4 )
A_2 ( 3 , 7 )
B_1 ( 5 , 8 )
B_2 ( 9 , 5 )
C_1 ( 6 , 2 )
C_2 ( 4 , 9 )
( 2 , 4 )
0
4
7
8
6
7
( 4 , 8 )
6
2
1
8
8
1
( 7 , 3 )
6
8
7
4
2
9
第二次迭代 : 步骤 ( 3 ) 聚类分组

1 . 聚类分组 : 根据计算出的 , 每个样本与

3

个中心点的距离 , 将样本划分到 距离该样本最近的中心点 对应的分组中 ;

A 1 ( 2 , 4 ) A_1 ( 2 , 4 ) A1​(2,4)

A 2 ( 3 , 7 ) A_2 ( 3 , 7 ) A2​(3,7)

B 1 ( 5 , 8 ) B_1 ( 5 , 8 ) B1​(5,8)

B 2 ( 9 , 5 ) B_2 ( 9 , 5 ) B2​(9,5)

C 1 ( 6 , 2 ) C_1 ( 6 , 2 ) C1​(6,2)

C 2 ( 4 , 9 ) C_2 ( 4 , 9 ) C2​(4,9)

( 2 , 4 ) ( 2 , 4 ) (2,4)

0 0 0

4 4 4

7 7 7

8 8 8

6 6 6

7 7 7

( 4 , 8 ) ( 4 , 8 ) (4,8)

6 6 6

2 2 2

1 1 1

8 8 8

8 8 8

1 1 1

( 7 , 3 ) ( 7 , 3 ) (7,3)

6 6 6

8 8 8

7 7 7

4 4 4

2 2 2

9 9 9

A_1 ( 2 , 4 )
A_2 ( 3 , 7 )
B_1 ( 5 , 8 )
B_2 ( 9 , 5 )
C_1 ( 6 , 2 )
C_2 ( 4 , 9 )
( 2 , 4 )
0
4
7
8
6
7
( 4 , 8 )
6
2
1
8
8
1
( 7 , 3 )
6
8
7
4
2
9

2 . 根据表格中的距离 , 为每个样本分组 :

①

A_1 ( 2 , 4 )

距离

( 2 , 4 )

中心点最近 , 划分到 聚类

1

中 ;

②

A_2 ( 3 , 7 )

距离

( 4 , 8 )

中心点最近 , 划分到 聚类

2

中 ;

③

B_1 ( 5 , 8 )

距离

( 4 , 8 )

中心点最近 , 划分到 聚类

2

中 ;

④

B_2 ( 9 , 5 )

距离

( 7 , 3 )

中心点最近 , 划分到 聚类

3

中 ;

⑤

C_1 ( 6 , 2 )

距离

( 7 , 3 )

中心点最近 , 划分到 聚类

3

中 ;

⑥

C_2 ( 4 , 9 )

距离

( 4 , 8 )

中心点最近 , 划分到 聚类

2

中 ;

3 . 最终的聚类分组为 :

① 聚类

1

:

\{ A_1 \}

② 聚类

2

:

\{ A_2 , B_1 , C_2 \}

③ 聚类

3

:

\{ B_2 , C_1 \}

第二次迭代的聚类分组 , 与第一次迭代的聚类分组 , 没有改变 , 说明聚类算法分析结果已经收敛 , 该聚类结果就是最终的结果 ;

K-Means 迭代总结

1 . 第一次迭代 :

① 设置中心点 : 设置了

3

个初始中心点 ,

A_1 ( 2 , 4 )

对应聚类

1

中心点 ,

B_1 ( 5 , 8 )

对应聚类

2

中心点 ,

C_1 ( 6 , 2 )

对应聚类

3

中心点 ;

② 计算中心点距离 : 然后就算

6

个样本距离这

3

个中心点的距离 ;

③ 根据距离聚类分组 : 每个样本取距离最近的

1

个中心点 , 将该样本分类成该中心点对应的聚类分组 , 聚类分组结果是 , 聚类

1

:

\{ A_1 \}

, 聚类

2

:

\{ A_2 , B_1 , C_2 \}

, 聚类

3

:

\{ B_2 , C_1 \}

;

2 . 第二次迭代 :

① 计算中心点 : 根据第一次迭代的聚类分组结果计算 3 3 3 个中心点 , ( 2 , 4 ) ( 2 , 4 ) (2,4) 对应聚类 1 1 1 中心点 , ( 4 , 8 ) 对应聚类 2 2 2 中心点 , ( 7 , 3 ) ( 7 , 3 ) (7,3) 对应聚类 3 3 3 中心点 ;

② 计算中心点距离 : 然后就算

6

个样本距离这

3

个中心点的距离 ;

③ 根据距离聚类分组 : 每个样本取距离最近的

1

个中心点 , 将该样本分类成该中心点对应的聚类分组 , 聚类分组结果是 , 聚类

1

:

\{ A_1 \}

, 聚类

2

:

\{ A_2 , B_1 , C_2 \}

, 聚类

3

:

\{ B_2 , C_1 \}

;

3 . 最终结果 : 经过

2

次迭代 , 发现 , 根据最初选择中心点 , 进行聚类分组的结果 , 就是最终的结果 , 迭代

2

次的分组结果相同 , 说明聚类算法已经收敛 , 此时的聚类结果就是最终结果 , 聚类算法终止 ;

K-Means 初始中心点选择方案

1 . 初始中心点选择 :

① 初始种子 : 初始的中心点 , 又称为种子 , 如果种子选择的好 , 迭代的次数就会非常少 , 迭代的最少次数为

2

, 如上面的示例 ;

② 种子选择影响 : 初始种子选择的好坏 , 即影响算法收敛的速度 , 又影响聚类结果的质量 ; 选择的好 , 迭代

2

次 , 算法收敛 , 得到最终结果 , 并且聚类效果很好 ; 选择的不好 , 迭代很多次才收敛 , 并且聚类效果很差 ;

2 . 初始中心点选择方案 :

① 随机选择 ;

② 使用已知聚类算法的结果 ;

③ 爬山算法 : K-Means 采用的是爬山算法 , 只找局部最优的中心点 ;

K-Means 算法优缺点

1 . K-Means 算法优点 :

① 算法可扩展性高 : 算法复杂度随数据量增加 , 而线性增加 ;

② 算法的复杂度 : K-Means 的算法复杂度是

O(tkn)

,

n

是数据样本个数 ,

k

是聚类分组的个数 ,

t

是迭代次数 ,

t

一般不超过

n

;

2 . K-Means 算法缺点 :

③ 事先必须设定聚类个数 : K-Means 的聚类分组的个数, 必须事先确定 , 有些应用场景中 , 事先是不知道聚类个数的 ;

④ 有些中心点难以确定 : 有些数据类型的中心点不好确定 , 如字符型的数据 , 离散型数据 , 布尔值数据 等 ;

⑤ 鲁棒性差 : 对于数据样本中的噪音数据 , 异常数据 , 不能有效的排除这些数据的干扰 ;

⑥ 局限性 : 只能处理凸状 , 或 球状分布的样本数据 , 对于 凹形分布 的样本数据 , 无法有效的进行聚类分析 ;

K-Means 算法变种

1 . K-Means 方法有很多变种 :

① K_Modes : 处理离散型的属性值 , 如字符型数据等 ;

② K-Prototypes : 处理 离散型 或 连续型 的属性 ;

③ K-Medoids : 其计算中心点不是使用算术平均值 , 其使用的是中间值 ;

2 . K-Means 变种算法 与 k-Means 算法的区别与联系 :

① 原理相同 : 这些变种算法 与 K-Means 算法原理基本相同 ;

② 中心点选择不同 : 变种算法 与 原算法 最初的中心点选择不同 ;

③ 距离计算方式不同 : K-Means 使用曼哈顿距离 , 变种算法可能使用 欧几里得距离 , 明科斯基距离 , 边际距离 等 ;

④ 计算聚类中心点策略不同 : K-Means 算法中使用算术平均 , 有的使用中间值 ;

本文参与 腾讯云自媒体分享计划，分享自作者个人站点/博客。
原始发表：2020-05-03，如有侵权请联系 cloudcommunity@tencent.com 删除
数据挖掘
聚类算法
表格
数据
算法

本文分享自 作者个人站点/博客 前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与 腾讯云自媒体分享计划  ，欢迎热爱写作的你一起参与！

数据挖掘
聚类算法
表格
数据
算法
评论
登录后参与评论
0 条评论
热度
最新
登录 后参与评论
推荐阅读
LV.
文章
0
获赞
0
目录
  • 文章目
    • K-Means 二维数据 聚类分析 数据样本及聚类要求
      • 二维数据曼哈顿距离计算
        • K-Means 算法 步骤
          • 第一次迭代 : 步骤 ( 1 ) 中心点初始化
            • 第一次迭代 : 步骤 ( 2 ) 计算距离
              • 第一次迭代 : 步骤 ( 3 ) 聚类分组
                • 第二次迭代 : 步骤 ( 1 ) 中心点初始化
                  • 第二次迭代 : 步骤 ( 2 ) 计算距离
                    • 第二次迭代 : 步骤 ( 3 ) 聚类分组
                      • K-Means 迭代总结
                        • K-Means 初始中心点选择方案
                          • K-Means 算法优缺点
                            • K-Means 算法变种
                            领券

                            腾讯云开发者

                            扫码关注腾讯云开发者

                            扫码关注腾讯云开发者

                            领取腾讯云代金券

                            热门产品

                            热门推荐

                            更多推荐

                            Copyright © 2013 - 2024 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有 

                            深圳市腾讯计算机系统有限公司 ICP备案/许可证号：粤B2-20090059 深公网安备号 44030502008569

                            腾讯云计算（北京）有限责任公司 京ICP证150476号 |  京ICP备11018762号 | 京公网安备号11010802020287

                            问题归档专栏文章快讯文章归档关键词归档开发者手册归档开发者手册 Section 归档

                            Copyright © 2013 - 2024 Tencent Cloud.

                            All Rights Reserved. 腾讯云 版权所有

                            登录 后参与评论