DS二叉树--层次遍历
题目描述
层次遍历二叉树,是从根结点开始遍历,按层次次序“自上而下,从左至右”访问树中的各结点。
建树方法采用“先序遍历+空树用0表示”的方法
要求:采用队列对象实现,函数框架如下:

输入
第一行输入一个整数t,表示有t个测试数据
第二行起输入二叉树先序遍历的结果,空树用字符‘0’表示,输入t行
输出
逐行输出每个二叉树的层次遍历结果
输入样例1
2 AB0C00D00 ABCD00E000FG00H0I00
输出样例1
ABDC ABFCGHDEI
思路分析
首先把树给建立起来,递归建立树的每个节点,先建立数据,再递归建立左子树,然后递归建立右子树,递归结束的条件是到了字符串末尾或者遇到字符0。
层次遍历实际上就是广度遍历,就是BFS搜索。
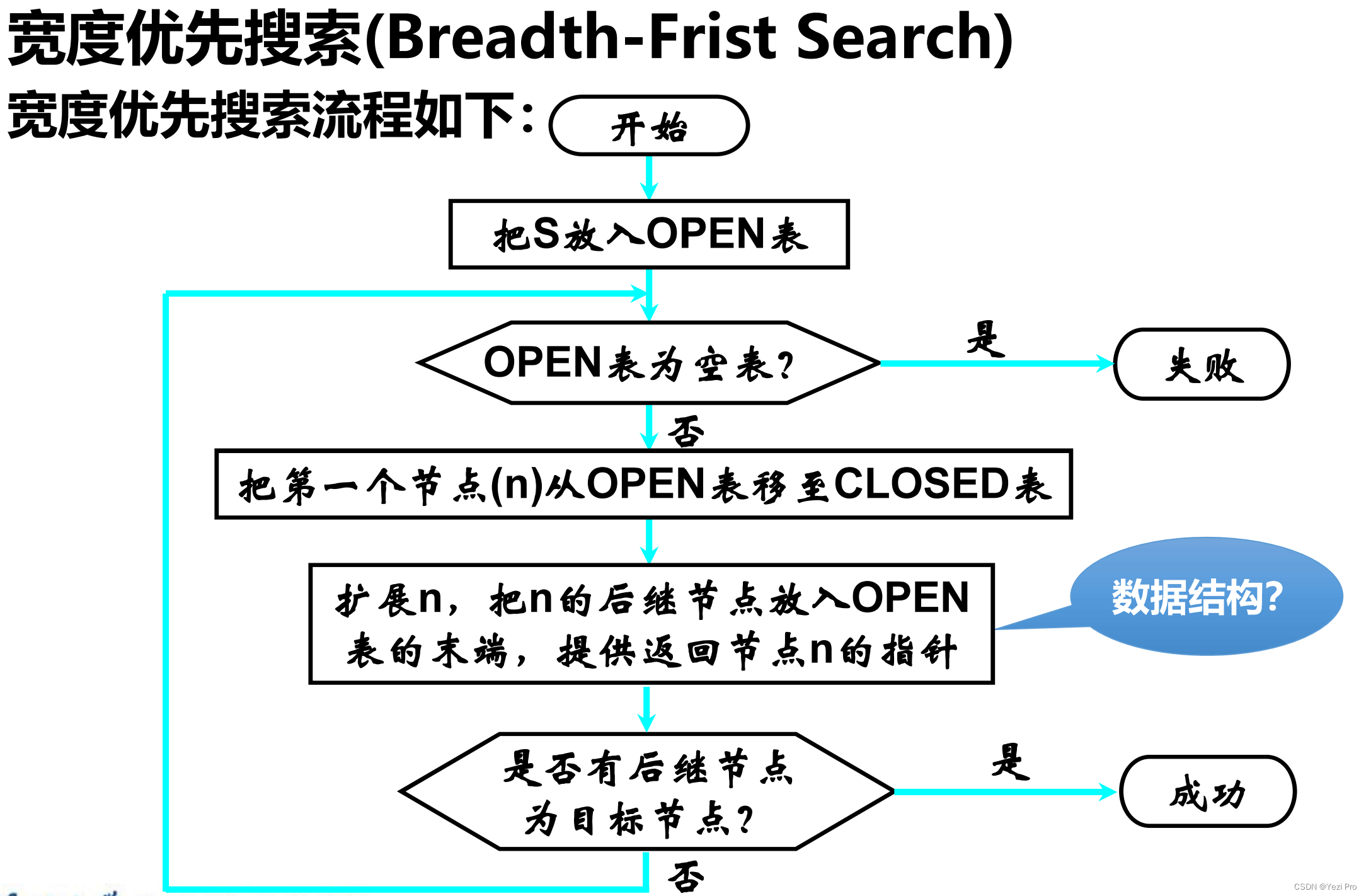
BFS是用队列作为存储的数据结构。
先将开始遍历的首节点入队,然后开始循环遍历,循环跳出的条件是队列为空。
在循环里面,取队首元素,出队,输出数据,然后将所有子树节点入队,循环操作下去完事。
AC代码
#include <iostream>
#include <string>
#include <queue>
using namespace std;
class BiTreeNode {
public:
char data; //数据域
BiTreeNode *leftChild, *rightChild; //左右子树指针
BiTreeNode():leftChild(NULL), rightChild(NULL){}
~BiTreeNode() {}
};
class BiTree {
private:
BiTreeNode *root; //根结点指针
string sTree; //建树字符串
int pos; //标识建树字符串的当前字符位置
BiTreeNode * CreateTree();//建树私有函数
public:
BiTree():root(NULL) {};
void Create(string vArray); //建树公有接口,参数是特定的先序遍历字符串
void LevelOrder();
void LevelOrder(BiTreeNode*T);
};
void BiTree::Create(string vArray)
{ pos=0;
sTree.assign(vArray); //把参数保存到内部字符串
root = CreateTree(); //建树成功后root指向根结点
}
BiTreeNode* BiTree::CreateTree() {
if(pos==sTree.size()||sTree[pos]=='0'){
pos++;
return NULL;
}
BiTreeNode*T=new BiTreeNode();
T->data=sTree[pos++];
T->leftChild=CreateTree();
T->rightChild=CreateTree();
return T;
}
void BiTree::LevelOrder() { LevelOrder(root);}
void BiTree::LevelOrder(BiTreeNode *T) {
queue<BiTreeNode*>tq;
BiTreeNode*p=T;
if(p)
tq.push(p);
while(!tq.empty()){
p=tq.front();
tq.pop();
if(p){
cout<<p->data;
tq.push(p->leftChild);
tq.push(p->rightChild);
}
}
cout<<endl;
}
int main()
{ int t;
string vArray;
cin>>t;
while(t--)
{ cin>>vArray;
BiTree myTree;
myTree.Create(vArray);
myTree.LevelOrder();
}
return 0;
}本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2022-10-25,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

