一文看懂 LLaMA 中的旋转式位置编码(Rotary Position Embedding)
一文看懂 LLaMA 中的旋转式位置编码(Rotary Position Embedding)
BBuf
发布于 2023-08-22 08:38:45
发布于 2023-08-22 08:38:45
旋转式位置编码(RoPE)最早是论文[1]提出的一种能够将相对位置信息依赖集成到 self-attention 中并提升 transformer 架构性能的位置编码方式。而目前很火的 LLaMA 模型也是采用该位置编码方式。
接下来结合代码和论文来解读一下 RoPE。
基本概念
首先论文中定义一个长度为 N 的输入序列为:
其中 wi 表示输入序列中第 i 个 token,而输入序列 SN 对应的 embedding 表示为:
其中 xi 表示第 i 个 token wi 对应的 d 维词嵌入向量。
接着在做 self-attention 之前,会用词嵌入向量计算 q, k, v 向量同时加入位置信息,函数公式表达如下:
其中 qm 表示第 m 个 token 对应的词向量 xm 集成位置信息 m 之后的 query 向量。而 kn 和 vn 则表示第 n 个 token 对应的词向量 xn 集成位置信息 n 之后的 key 和 value 向量。
而基于 transformer 的位置编码方法都是着重于构造一个合适的 f{q,k,v} 函数形式。
而计算第 m 个词嵌入向量 xm 对应的 self-attention 输出结果,就是 qm 和其他 kn 都计算一个 attention score ,然后再将 attention score 乘以对应的 vn 再求和得到输出向量 om:
绝对位置编码
对于位置编码,常规的做法是在计算 query, key 和 value 向量之前,会计算一个位置编码向量 pi 加到词嵌入 xi 上,位置编码向量 pi 同样也是 d 维向量,然后再乘以对应的变换矩阵 W{q,k,v}:
而经典的位置编码向量 pi 的计算方式是:
其中 p_{i,2t} 表示位置 d 维度向量 pi 中的第 2t 个元素也就是偶数索引位置的计算公式,而 p_{i,2t+1} 就对应奇数索引位置的计算公式。
python 代码如下:
# position 就对应 token 序列中的位置索引 i
# hidden_dim 就对应词嵌入维度大小 d
# seq_len 表示 token 序列长度
def get_position_angle_vec(position):
return [position / np.power(10000, 2 * (hid_j // 2) / hidden_dim) for hid_j in range(hidden_dim)]
# position_angle_vecs.shape = [seq_len, hidden_dim]
position_angle_vecs = np.array([get_position_angle_vec(pos_i) for pos_i in range(seq_len)])
# 分别计算奇偶索引位置对应的 sin 和 cos 值
position_angle_vecs[:, 0::2] = np.sin(position_angle_vecs[:, 0::2]) # dim 2t
position_angle_vecs[:, 1::2] = np.cos(position_angle_vecs[:, 1::2]) # dim 2t+1
# positional_embeddings.shape = [1, seq_len, hidden_dim]
positional_embeddings = torch.FloatTensor(position_angle_vecs).unsqueeze(0)
旋转式位置编码
接着论文中提出为了能利用上 token 之间的相对位置信息,假定 query 向量 qm 和 key 向量 kn 之间的内积操作可以被一个函数 g 表示,该函数 g 的输入是词嵌入向量 xm , xn 和它们之间的相对位置 m - n:
接下来的目标就是找到一个等价的位置编码方式,从而使得上述关系成立。
假定现在词嵌入向量的维度是两维 d=2,这样就可以利用上2维度平面上的向量的几何性质,然后论文中提出了一个满足上述关系的 f 和 g 的形式如下:
上面的公式一眼看过去感觉很复杂,怎么理解呢?
首先我们得先了解一下基本的复数相关知识。
首先看到上述 f 和 g 公式中有个指数函数
这个其实是欧拉公式 [2],其中 x 表示任意实数, e 是自然对数的底数,i 是复数中的虚数单位,则根据欧拉公式有:
上述指数函数可以表示为实部为 cosx,虚部为 sinx 的一个复数,欧拉公式 [2] 建立了指数函数、三角函数和复数之间的桥梁。
则上述 f 和 g 公式中的
然后我们看回公式:
其中 Wq 是个二维矩阵,xm 是个二维向量,相乘的结果也是一个二维向量,这里用 qm 表示:
然后首先将 qm 表示成复数形式:
接着
其实就是两个复数相乘:
我们首先来复习一下复数乘法的性质:
可以看到,复数乘法也是用的分配律,还有用到了复数的一个性质:
然后就有:
将结果重新表达成实数向量形式就是:
相信读者看到这里会发现这不就是 query 向量乘以了一个旋转矩阵[5]吗?
这就是为什么叫做旋转式位置编码的原因。
同理可得 key 向量 kn :
最后还有个函数 g:
其中 Re[x] 表示一个复数 x 的实部部分,而
则表示复数
的共轭,复习一下共轭复数的定义:
所以可得:
继续可得:
ok,接下来我们就要证明函数 g 的计算公式是成立的。
首先回顾一下 attention 操作, 位置 m 的 query 和位置 n 的 key 会做一个内积操作:
接着继续之前先复习一下三角函数的一些性质[3]:
好了回到上面那坨式子,我们整理一下:
这就证明上述关系是成立的,位置 m 的 query 和位置 n 的 key 的内积就是函数 g。
然后上面的讲解是假定的词嵌入维度是2维向量,而对于d >= 2 的通用情况,则是将词嵌入向量元素按照两两一组分组,每组应用同样的旋转操作且每组的旋转角度计算方式如下:
所以简单来说 RoPE 的 self-attention 操作的流程是,对于 token 序列中的每个词嵌入向量,首先计算其对应的 query 和 key 向量,然后对每个 token 位置都计算对应的旋转位置编码,接着对每个 token 位置的 query 和 key 向量的元素按照 两两一组 应用旋转变换,最后再计算 query 和 key 之间的内积得到 self-attention 的计算结果。
论文中有个很直观的图片展示了旋转变换的过程:
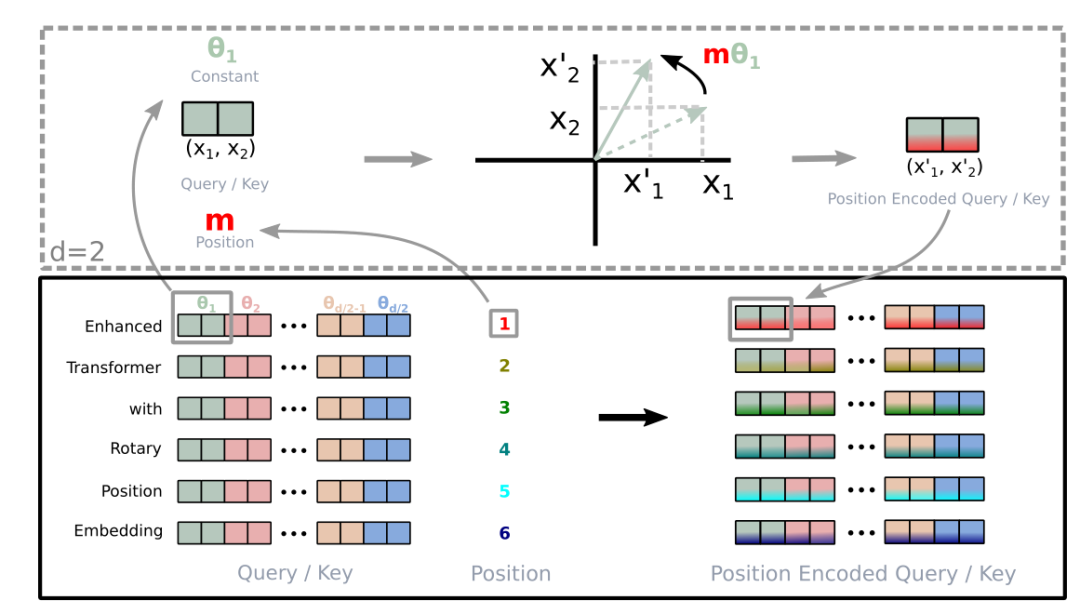
LLaMA 官方实现代码 [4] 如下(经过简化):
def precompute_freqs_cis(dim: int, seq_len: int, theta: float = 10000.0):
# 计算词向量元素两两分组之后,每组元素对应的旋转角度
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
# 生成 token 序列索引 t = [0, 1,..., seq_len-1]
t = torch.arange(seq_len, device=freqs.device)
# freqs.shape = [seq_len, dim // 2]
freqs = torch.outer(t, freqs).float()
# torch.polar 的文档
# https://pytorch.org/docs/stable/generated/torch.polar.html
# 计算结果是个复数向量
# 假设 freqs = [x, y]
# 则 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i]
freqs_cis = torch.polar(torch.ones_like(freqs), freqs)
return freqs_cis
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
# xq.shape = [batch_size, seq_len, dim]
# xq_.shape = [batch_size, seq_len, dim // 2, 2]
xq_ = xq.float().reshape(*xq.shape[:-1], -1, 2)
xk_ = xk.float().reshape(*xk.shape[:-1], -1, 2)
# 转为复数域
xq_ = torch.view_as_complex(xq_)
xk_ = torch.view_as_complex(xk_)
# 应用旋转操作,然后将结果转回实数域
# xq_out.shape = [batch_size, seq_len, dim]
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(2)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(2)
return xq_out.type_as(xq), xk_out.type_as(xk)
class Attention(nn.Module):
def __init__(self, args: ModelArgs):
super().__init__()
self.wq = Linear(...)
self.wk = Linear(...)
self.wv = Linear(...)
self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2)
def forward(self, x: torch.Tensor):
bsz, seqlen, _ = x.shape
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(batch_size, seq_len, dim)
xk = xk.view(batch_size, seq_len, dim)
xv = xv.view(batch_size, seq_len, dim)
# attention 操作之前,应用旋转位置编码
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
# scores.shape = (batch_size, seq_len, seqlen)
scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim)
scores = F.softmax(scores.float(), dim=-1)
output = torch.matmul(scores, xv) # (batch_size, seq_len, dim)
# ......
可以看到 LLaMA 的官方实现代码和论文 [1] 中的描述是一致的。
参考资料
- [1] https://arxiv.org/pdf/2104.09864.pdf
- [2] https://en.wikipedia.org/wiki/Euler's_formula
- [3] https://en.wikipedia.org/wiki/List_of_trigonometric_identities
- [4] https://github.com/facebookresearch/llama/tree/main
- [5] https://zh.wikipedia.org/wiki/旋转矩阵
本文参与 腾讯云自媒体同步曝光计划,分享自微信公众号。
原始发表:2023-07-09,如有侵权请联系 cloudcommunity@tencent.com 删除
本文分享自 GiantPandaCV 微信公众号,前往查看
如有侵权,请联系 cloudcommunity@tencent.com 删除。
本文参与 腾讯云自媒体同步曝光计划 ,欢迎热爱写作的你一起参与!
评论
登录后参与评论
推荐阅读
目录

