有限元 | 梁的弹性稳定分析(一)

fem178

发布于 2024-04-10 10:23:07

890

发布于 2024-04-10 10:23:07

文章被收录于专栏：数值分析与有限元编程数值分析与有限元编程

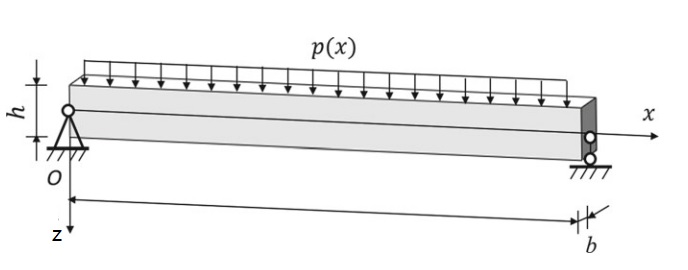
▲图1

图1为受分布载荷作用的简支梁，该问题平衡微分方程的如下

-EI\frac {d^4 \omega}{d x^4} + p(x) = 0

该平衡方程建立在未变形时，即忽略了变形的影响。

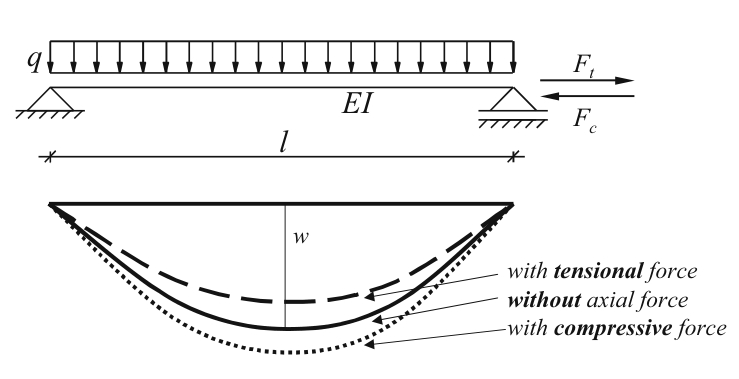
▲图2

如图2所示，简支梁在横向均布荷载

作用下产生的弯矩为

M_0(x)

，挠度为

\omega_0(x)

。轴向荷载F会在

\omega_0(x)

的基础上产生力矩

\Delta M(x) = F\omega_0(x)

如果

为拉力，则

\omega_0(x)

会减小，则最终弯矩范围

M_0 -F\omega_0 < M < M_0

如果

为压力，则

\omega_0(x)

会增加，则最终弯矩范围

M_0 < M < M_0+F\omega_0

可见细长梁在轴向力作用下的弯曲，有必要检查变形之后的平衡(即使变形很小)。

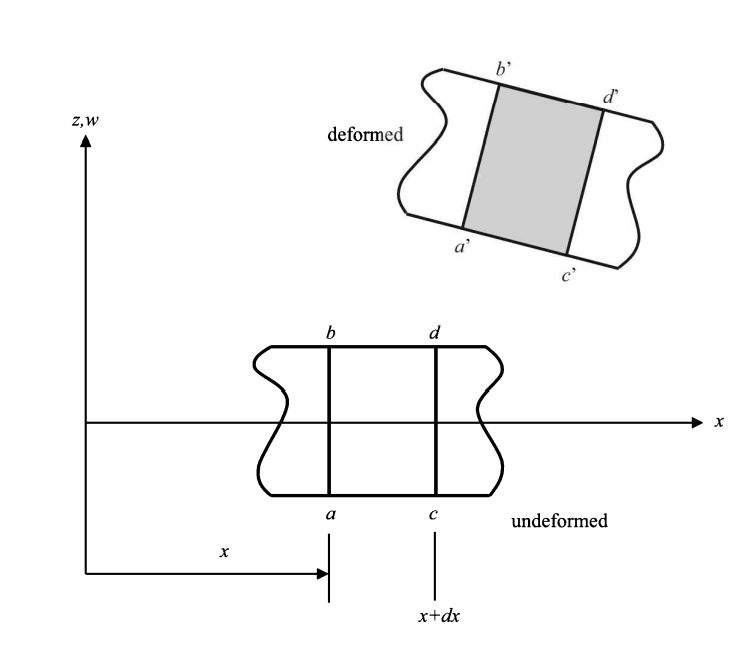
▲图3

如图3所示，细长梁上的任一微段

abdc

是其变形之前的位置,

a'b'd'c'

为变形后的位置。该微段的受力分析如图4所示

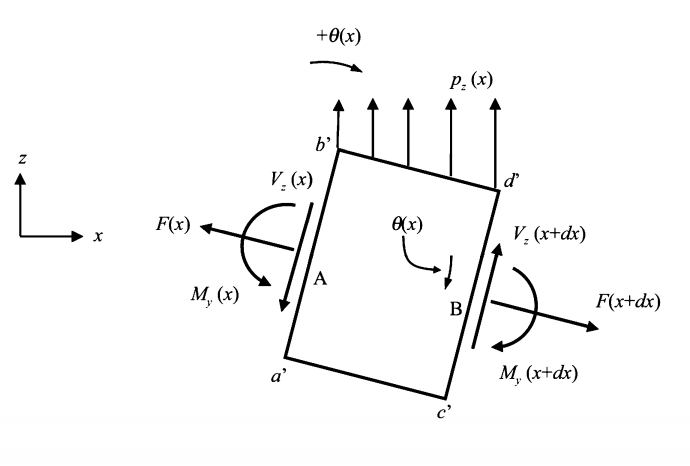
▲图4

由

\sum F_z =0

得

(F\sin\theta)_x - (F\sin\theta)_{x+dx}-(V_z \cos\theta)_x + (V_z \cos\theta)_{x+dx} +pdx = 0 \quad \cdots (1)

式中

\begin{split} (F\sin\theta)_{x+dx} &= (F\sin\theta)_x + \frac {\partial }{\partial x}(F\sin\theta)dx \\ (V_z \cos\theta)_{x+dx} &= (V_z \cos\theta)_x + \frac {\partial }{\partial x}(V_z \cos\theta)dx\\ \end{split} \quad \cdots (2)

(2)代入(1)得

[-\frac {\partial }{\partial x}(F\sin\theta) + \frac {\partial }{\partial x}(V_z \cos\theta) + p]dx = 0 \quad \cdots (3)

对于充分小的

\theta

，有

\sin\theta =\theta,\cos\theta = 1

，则(3)可写成

-\frac {\partial }{\partial x}(F\theta) + \frac {\partial V_z }{\partial x} + p =0 \quad \cdots (4)

注意到

\theta = - \frac {\partial \omega }{\partial x}

，(4)可写成

\frac {\partial }{\partial x}(F\frac {\partial \omega }{\partial x} ) + \frac {\partial V_z }{\partial x} + p =0 \quad \cdots (5)

关于B点的力矩平衡，有

M_y(x+dx)-M_y(x)-V_z(x)|AB|+pdx \frac 12(|AB|\cos\theta) = 0\quad \cdots (6)

注意到

M_y(x+dx) = M_y(x) + \frac {\partial M_y(x) }{\partial x}dx

由于

|AB|\cos\theta = dx

，(6)可以写成

[\frac {\partial M_y(x) }{\partial x}-V_z(x)]dx + \frac 12p dx^2 =0 \quad \cdots (7)

忽略(7)的高阶项，有

\frac {\partial M_y(x) }{\partial x} = V_z\quad \cdots (8)

(8)代入(5)有

\frac {\partial^2 M_y(x) }{\partial x^2} + \frac {\partial }{\partial x}(F\frac {\partial \omega }{\partial x} ) + p = 0 \quad \cdots (9)

(9)就是考虑轴向荷载时梁的平衡微分方程。

本文参与腾讯云自媒体分享计划，分享自微信公众号。

原始发表：2024-03-31，如有侵权请联系 cloudcommunity@tencent.com 删除

基础

partial

split

sum

本文分享自数值分析与有限元编程微信公众号，前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体分享计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度

有限元 | 梁的弹性稳定分析(一)

有限元 | 梁的弹性稳定分析(一)

社区

活动

资源

关于

腾讯云开发者

热门产品

热门推荐

更多推荐