一、向量和矩阵的基本运算 1、简单变换 \boldsymbol{x} =\begin{bmatrix}x\\y\end{bmatrix} 1. 平移变换 \begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}x\\y\end{bmatrix} + \begin{bmatrix}a\\b\end{bmatrix}
将向量
\begin{bmatrix}a\\b\end{bmatrix} 加到
\begin{bmatrix}x\\y\end{bmatrix} 上,得到平移后的新向量
\begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}x+a\\y+b\end{bmatrix} 。其中
a 和
b 分别为x方向和y方向的平移量 。
2. 缩放变换 \begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}s_x & 0\\0 & s_y\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix} = \begin{bmatrix}s_xx\\s_yy\end{bmatrix}
通过缩放矩阵
\begin{bmatrix}s_x & 0\\0 & s_y\end{bmatrix} 乘以
\begin{bmatrix}x\\y\end{bmatrix} ,可以得到缩放后的向量
\begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}s_xx\\s_yy\end{bmatrix} 。其中
s_x 和
s_y 分别为x方向和y方向的缩放比例 。
3. 旋转变换 \begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}
通过旋转矩阵
\begin{bmatrix}\cos\theta & -\sin\theta\\\sin\theta & \cos\theta\end{bmatrix} 乘以
\begin{bmatrix}x\\y\end{bmatrix} ,可以得到绕原点逆时针旋转
\theta 角度 后的向量
\begin{bmatrix}x'\\y'\end{bmatrix} 。
4. 一般线性变换 \begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}a & b\\c & d\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix} = \begin{bmatrix}ax+by\\cx+dy\end{bmatrix}
通过一个2x2变换矩阵
\begin{bmatrix}a & b\\c & d\end{bmatrix} 乘以
\begin{bmatrix}x\\y\end{bmatrix} ,可以得到一个新的变换后向量
\begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}ax+by\\cx+dy\end{bmatrix} ,这个变换矩阵可以表示缩放、旋转、错切等线性变换的组合 。
2、齐次坐标 0. 齐次坐标表示 在使用齐次坐标表示时,我们将n维欧几里得空间中的点
(x_1, x_2, \dots, x_n) 表示为
(n+1) 维的齐次坐标形式
(x_1, x_2, \dots, x_n, 1) ,在原始坐标的基础上添加一个1作为最后一个分量。
\begin{bmatrix}x\\y\\1\end{bmatrix} 表示,即在笛卡尔坐标
\begin{bmatrix}x\\y\end{bmatrix} 的基础上添加一个1作为最后一个分量;
\begin{bmatrix}x\\y\\z\\1\end{bmatrix} 表示,即在笛卡尔坐标
\begin{bmatrix}x\\y\\z\end{bmatrix} 的基础上添加一个1作为最后一个分量。
1. 2D点的齐次坐标变换 \begin{bmatrix}a & b & c\\d & e & f\\0 & 0 & 1\end{bmatrix} \begin{bmatrix}x'\\y'\\1\end{bmatrix} = \begin{bmatrix}a & b & c\\d & e & f\\0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}ax+by+c\\dx+ey+f\\1\end{bmatrix} 该变换矩阵包含了三个部分:
\begin{bmatrix}c\\f\end{bmatrix} \begin{bmatrix}a & b\\d & e\end{bmatrix} 构成的2x2子矩阵)
缩放分量(a, b, d, e的大小) 当这些元素的值大于1时,会放大相应方向的坐标;小于1时,会缩小。 2. 投影空间 (x, y, w) 引入一个三维投影空间,由
x 、
y 和
w 三个坐标构成,用
\begin{bmatrix}x\\y\\w\end{bmatrix} 表示。
其中
w=0 表示无穷远的点,即所有投影线的汇聚点所在位置。
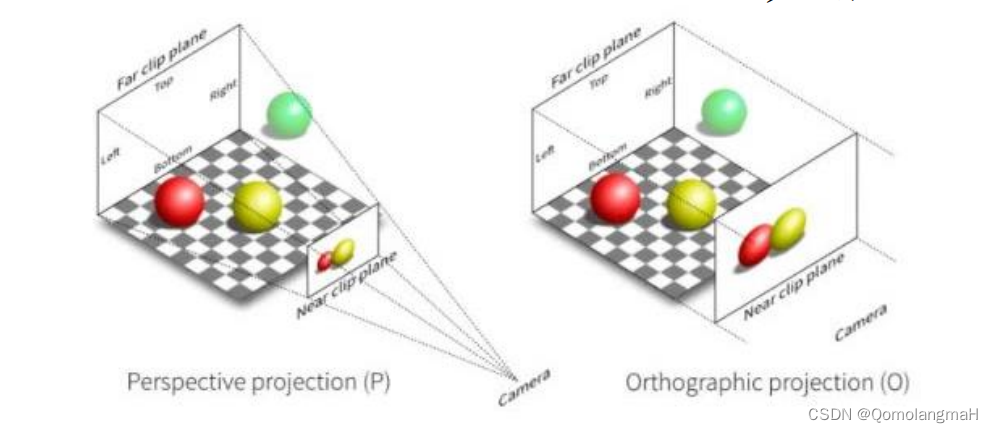
左图展示了透视投影 (Perspective projection)的情况,所有投影线从场景中的点汇聚于一个无穷远点,这种投影方式可以提供深度信息和真实的景深感。 \begin{bmatrix}x'\\y'\\w'\end{bmatrix} = \begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\begin{bmatrix}x\\y\\w\end{bmatrix} 右图展示了正交投影 (Orthographic projection)的情况,投影线都是平行的,没有汇聚点,无法获得真实的景深感,但可以保持投影后物体的形状不变形。 正交投影常用于工程制图等需要保持形状的场合,表达式为:
\begin{bmatrix}x'\\y'\\w'\end{bmatrix} = \begin{bmatrix}a&b&0\\c&d&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\w\end{bmatrix} 这种投影空间和投影变换在计算机图形学中被广泛使用,用于将三维物体投影到二维平面上进行显示。
3. 2D直线的齐次坐标表示 a. 直线的参数方程表示 l = (a, b, c)\\x\cdot l = ax + by + c = 0 其中
(a, b, c) 是直线的系数,任意一点
(x, y) 代入方程,结果为0,则该点位于该直线上。
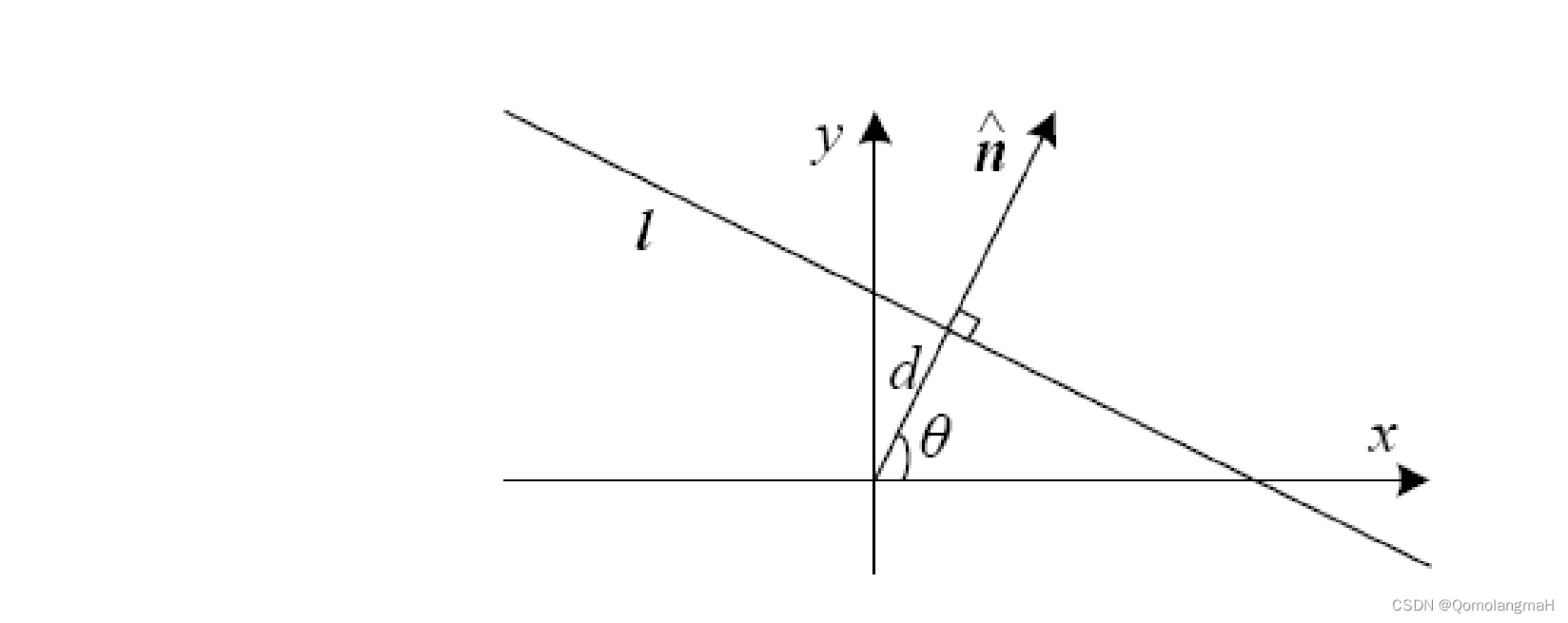
b. 直线的法向量和原点距离表示 l = (n_x, n_y, d) = (\vec{n}, d) \quad \text{with} \ \|\vec{n}\| = 1 其中
\vec{n} = (n_x, n_y) = (\cos\theta, \sin\theta) 表示直线的法向量,即垂直于直线方向的单位向量,
d 表示直线到原点的有符号距离。
这种表示直观地描述了直线的性质:
\vec{n} 给出了直线的方向
d 给出了直线到原点的距离,取正负号表示直线在原点的两侧
法向量和原点距离表示对于直线的各种几何运算都很有用,例如求直线交点、判断点和直线的位置关系等。通过矩阵变换,可以很自然地对直线进行旋转、平移等操作。
4. 叉积算子 两条直线的表示:
给定两条直线 \tilde{l}_1 和
\tilde{l}_2 的齐次坐标表示。
交点的计算:
两条直线 \tilde{l}_1 和
\tilde{l}_2 的交点
\tilde{x} 可以通过它们的外积(叉积)求得:
\tilde{x} = \tilde{l}_1 \times \tilde{l}_2
其中,外积的计算方式为:
\tilde{l}_1 = (\tilde{x}_1, \tilde{y}_1, \tilde{a}_1) \tilde{l}_2 = (\tilde{x}_2, \tilde{y}_2, \tilde{a}_2) \tilde{x} = \tilde{l}_1 \times \tilde{l}_2 = 这种利用直线的齐次坐标表示求交点的方法,可以自然地推广到三维空间,求两条三维直线或平面的交点。同理,在三维情况下,交点坐标为两个直线或平面的齐次坐标外积。
5. 平行线可以相交 \begin{cases} Ax + By + C = 0\\ Ax + By + D = 0 \end{cases} \begin{cases} A \dfrac{x}{w} + B \dfrac{y}{w} + C = 0\\ A \dfrac{x}{w} + B \dfrac{y}{w} + D = 0 \end{cases} \quad\iff\quad \begin{cases} Ax + By + Cw = 0\\ Ax + By + Dw = 0 \end{cases} 在这种表示下,两条直线的齐次坐标分别为
(A, B, C) 和
(A, B, D) 。
w=0 时,对应的是无穷远点,两条直线在这个点处相交