关于数据结构单链表

单链表作为最基础也是最常用的数据结构之一，在这门课程中占据着十分重要的地位。本文将对单链表这一章节的知识点进行总结，包括单链表的定义、基本操作、常见应用以及时间复杂度等方面。

一、单链表的定义和基本操作

单链表的定义：单链表由节点组成，每个节点包含数据和指向下一个节点的指针。

单链表是一种线性存储结构，相邻节点通过指针连接，每个节点只有一个指针指向下一个节点，最后一个节点的指针指向空。

1.单链表的插入操作：

单链表的插入操作可以在链表的头部或者指定位置插入一个新节点。具体步骤是先创建一个新节点，然后调整指针的指向，将新节点插入到链表中。

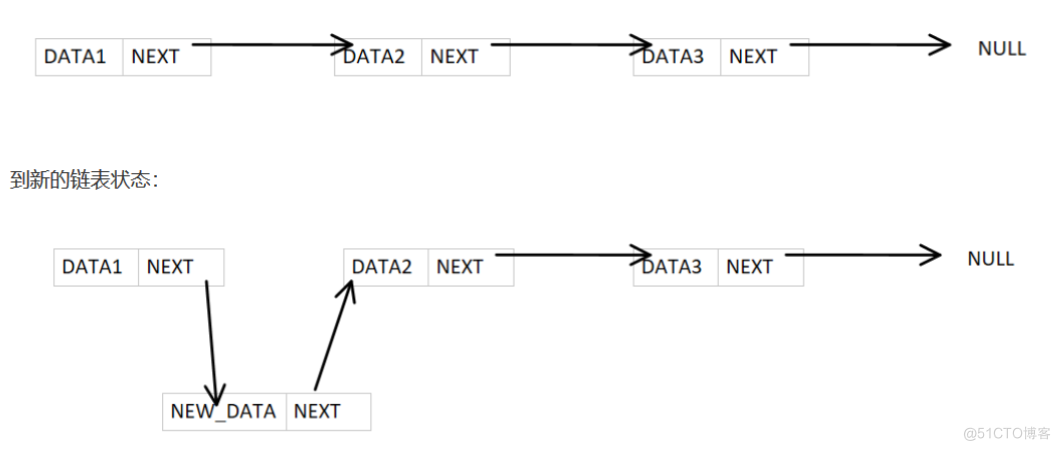
• 在头部插入节点：新节点的指针指向原来的头节点，然后将头节点更新为新节点。
• 在指定位置插入节点：找到指定位置的节点，将新节点的指针指向它的后继节点，然后将前驱节点的指针指向新节点。

如图，在DATA1和DATA2数据结点之中插入一个NEW_DATA数据结点：

关于数据结构单链表_单链表

//单链表的插入，在链表的第i个位置插入x的元素
  
LinkedList LinkedListInsert(LinkedList L,int i,int x) {
    Node *pre;                      //pre为前驱结点
    pre = L;
    int tempi = 0;
    for (tempi = 1; tempi < i; tempi++) {
        pre = pre->next;                 //查找第i个位置的前驱结点
    }
    Node *p;                                //插入的结点为p
    p = (Node *)malloc(sizeof(Node));
    p->data = x;
    p->next = pre->next;
    pre->next = p;
  
    return L;
}

2.单链表的删除操作：

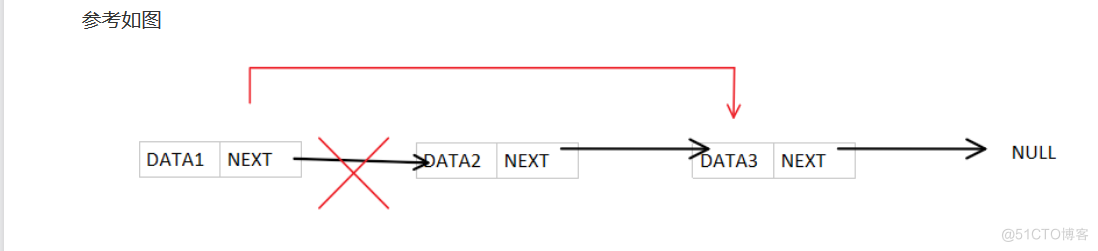
单链表的删除操作可以删除链表中的特定节点。需要找到要删除的节点的前驱节点，然后调整指针的指向，将目标节点从链表中删除。

• 删除头节点：将头节点更新为原来的下一个节点。
• 删除指定节点：找到指定节点的前驱节点，将其指针指向目标节点的后继节点。

关于数据结构单链表_数据结构与算法_02

//单链表的删除，在链表中删除值为x的元素

LinkedList LinkedListDelete(LinkedList L,int x) { Node *p,*pre; //pre为前驱结点，p为查找的结点。 p = L->next;

while(p->data != x) {              //查找值为x的元素
    pre = p;
    p = p->next;
}
pre->next = p->next;          //删除操作，将其前驱next指向其后继。
free(p);
 
return L;
}

3.单链表的搜索操作：

单链表的搜索操作可以在链表中查找特定值是否存在。需要遍历整个链表，依次比较节点的值，直到找到目标值或者链表结束。

• 遍历链表，比较节点的值和目标值，如果相等则返回节点的位置或其他信息。

4.单链表的遍历操作：

单链表的遍历操作可以按顺序访问链表中的每个节点。可以输出节点的值或者执行其他操作，如统计链表的长度、求和等。

• 从头节点开始，依次访问每个节点，直到链表结束。

二、单链表的常见应用

1.单链表实现栈：

栈是一种后进先出(LIFO)的数据结构，可以使用单链表的头部作为栈顶，通过插入和删除操作来实现栈的功能。

• 入栈操作：在链表的头部插入一个新节点。
• 出栈操作：删除链表的头部节点。

2.单链表实现队列：

队列是一种先进先出(FIFO)的数据结构，可以使用单链表的尾部作为队尾，通过插入和删除操作来实现队列的功能。

• 入队操作：在链表的尾部插入一个新节点。
• 出队操作：删除链表的头部节点。

3.单链表实现链表：

链表是一种非连续的数据结构，可以动态地增加或删除节点。由于单链表只需要改变指针的指向，因此插入和删除操作比较高效。

• 插入操作：在指定位置插入一个新节点。
• 删除操作：删除指定位置的节点。

4.单链表在算法中的应用：

单链表常用于解决链表相关的算法问题，如反转链表、合并链表、判断是否有环等。

三、单链表的时间复杂度

1. 插入、删除和搜索操作的平均时间复杂度是O(n)，其中n是链表的长度。因为单链表只能从头部开始遍历，所以这些操作需要线性的时间来查找目标节点。
2. 在特定情况下，插入和删除操作的时间复杂度可以是O(1)，例如在已知要插入或删除的节点的前驱节点的情况下。
3. 遍历操作的时间复杂度是O(n)，因为需要访问每个节点一次。

四、实际应用和选择合适的数据结构

1. 单链表具有灵活性和动态性，适用于插入和删除频繁、元素个数不确定的场景。
2. 如果需要频繁的搜索和访问操作，可能需要考虑其他数据结构，如数组或二叉搜索树。
3. 在实际应用中，我们需要根据问题需求选择合适的数据结构，以获得更高效的算法和程序设计。

通过学习单链表的定义、基本操作、常见应用以及时间复杂度等知识点，我们能够掌握单链表的核心概念和使用方法。了解单链表的特点和适用场景，能够在实际问题中灵活运用单链表解决各种需求。此外，也应该根据问题需求选择合适的数据结构，以提高算法的效率和程序的性能。

下面是关于单链表的练习题：

1. 在单链表的头部插入一个节点的代码实现是什么？ A. head = Node(data, head) B. head.next = Node(data) C. head.prev = Node(data) D. head = Node(head, data)
2. 在单链表的尾部插入一个节点的代码实现是什么？ A. tail = Node(data, tail) B. tail.next = Node(data) C. tail.prev = Node(data) D. tail = Node(tail, data)
3. 在单链表的指定位置插入一个节点的代码实现是什么？ A. prev_node = Node(data, prev_node.next) B. next_node = Node(data, next_node.next) C. prev_node.next = Node(data, prev_node.next) D. next_node.next = Node(data, next_node.next)
4. 如何删除单链表的头节点？ A. head = head.next B. head.prev = None C. head.next = None D. head = None
5. 如何删除单链表的尾节点？ A. tail.next = None B. tail.prev = tail C. tail = None D. tail.prev = None
6. 如何删除单链表的指定位置节点？ A. prev_node.next = prev_node.next.next B. next_node.next = None C. prev_node = None D. next_node = None
7. 如何判断单链表是否为空？ A. head is None B. tail is None C. head.next is None D. tail.next is None
8. 如何获取单链表的长度？ A. 遍历整个链表，计算节点个数 B. length = len(single_linked_list) C. length = tail + 1 D. length = head.length()
9. 如何判断两个单链表是否相等？ A. single_linked_list1 == single_linked_list2 B. 遍历整个链表，逐一比较节点数据 C. single_linked_list1.equals(single_linked_list2) D. single_linked_list1.length() == single_linked_list2.length()
10. 如何删除单链表中所有的节点？ A. single_linked_list.clear() B. head = None C. tail = None D. 遍历整个链表，逐一删除节点
11. 单链表和数组相比，插入和删除操作的效率如何？ A. 单链表更高效 B. 数组更高效 C. 速度相当 D. 取决于具体情况
12. 判断两个单链表是否相等的条件是什么？ A. 节点个数和数据全部相等 B. 只需判断节点个数相等 C. 节点个数相等且数据顺序相同 D. 取决于具体情况
13. 单链表的反转操作的代码实现是什么？ A. new_head = None; current = head;while current is not None: next_node = current.next current.next = new_head new_head = current current = next_nodehead = new_head B. tail = head; head = tail.prev C. head = tail; tail = head.next D. head.next = None
14. 在单链表中查找第一个满足特定条件的节点的代码实现是什么？ A. current = headwhile current is not None: if current.data == target: return current current = current.nextreturn None B. target = search(single_linked_list, target) C. target = delete(single_linked_list, target) D. target = insert_at_head(single_linked_list, target)
15. 在单链表中插入或删除一个节点后，需要更新哪个指针？ A. 头指针(head) B. 尾指针(tail) C. 下一个节点指针(next) D. 上一个节点指针(prev)
16. 如果一个单链表循环了，即尾节点指向了头节点，如何判断出现循环？ A. 使用快慢指针法判断是否存在环 B. 遍历整个链表，判断尾节点的下一个节点是否是头节点 C. 判断单链表的长度是否超过某一阈值 D. 判断链表中是否存在重复的节点
17. 单链表的插入和删除操作属于什么类型的数据结构基本操作？ A. 查询操作 B. 修改操作 C. 排序操作 D. 组合操作
18. 单链表的插入和删除操作可能涉及到的指针变动是什么？ A. 指向前驱节点的指针 B. 指向后继节点的指针 C. 指向头节点的指针 D. 指向尾节点的指针
19. 单链表的插入和删除操作的时间复杂度是多少？ A. O(1) B. O(n) C. O(log n) D. O(n log n)
20. 给出单链表的完整实现代码： A. 太长，无法给出具体实现 B. 链表操作的伪代码 C. 单链表的类定义和方法实现 D. 链表的结构体定义和函数声明

答案：

1. 在单链表的头部插入一个节点的代码实现是什么？ 答案：A. head = Node(data, head)
2. 在单链表的尾部插入一个节点的代码实现是什么？ 答案：B. tail.next = Node(data)
3. 在单链表的指定位置插入一个节点的代码实现是什么？ 答案：C. prev_node.next = Node(data, prev_node.next)
4. 如何删除单链表的头节点？ 答案：A. head = head.next
5. 如何删除单链表的尾节点？ 答案：C. tail = None
6. 如何删除单链表的指定位置节点？ 答案：A. prev_node.next = prev_node.next.next
7. 如何判断单链表是否为空？ 答案：A. head is None
8. 如何获取单链表的长度？ 答案：A. 遍历整个链表，计算节点个数
9. 如何判断两个单链表是否相等？ 答案：B. 遍历整个链表，逐一比较节点数据
10. 如何删除单链表中所有的节点？ 答案：D. 遍历整个链表，逐一删除节点
11. 单链表和数组相比，插入和删除操作的效率如何？ 答案：A. 单链表更高效
12. 判断两个单链表是否相等的条件是什么？ 答案：A. 节点个数和数据全部相等
13. 单链表的反转操作的代码实现是什么？ 答案：A. new_head = None; current = head;while current is not None: next_node = current.next current.next = new_head new_head = current current = next_nodehead = new_head
14. 在单链表中查找第一个满足特定条件的节点的代码实现是什么？ 答案：A. current = headwhile current is not None: if current.data == target: return current current = current.nextreturn None
15. 在单链表中插入或删除一个节点后，需要更新哪个指针？ 答案：A. 头指针(head)
16. 如果一个单链表循环了，即尾节点指向了头节点，如何判断出现循环？ 答案：A. 使用快慢指针法判断是否存在环
17. 单链表的插入和删除操作属于什么类型的数据结构基本操作？ 答案：B. 修改操作
18. 单链表的插入和删除操作可能涉及到的指针变动是什么？ 答案：B. 指向后继节点的指针
19. 单链表的插入和删除操作的时间复杂度是多少？ 答案：A. O(1)
20. 给出单链表的完整实现代码： 答案：C. 单链表的类定义和方法实现

图片以及代码来源：https://www.dotcpp.com/