【初阶数据结构篇】冒泡排序、快速排序

熬夜学编程的小王

发布于 2024-11-20 20:36:29

2730

须知

💬 欢迎讨论：如果你在学习过程中有任何问题或想法，欢迎在评论区留言，我们一起交流学习。你的支持是我继续创作的动力！ 👍 点赞、收藏与分享：觉得这篇文章对你有帮助吗？别忘了点赞、收藏并分享给更多的小伙伴哦！你们的支持是我不断进步的动力！ 🚀 分享给更多人：如果你觉得这篇文章对你有帮助，欢迎分享给更多对C++感兴趣的朋友，让我们一起进步！

本篇以排升序为例

1. 冒泡排序

动图理解：

1.1 分析

作为第一个接触的排序算法，冒泡排序想必大家已经很熟悉了总共n个数据，要排n-1趟第i（i从0开始取）趟要比较n-1-i次等差数列求和，最坏时间复杂度为O(n2) 定义exchange变量，当数组已经有序时不进入交换，直接跳出循环最好时间复杂度为O(n) 空间复杂度O(1)

1.2 示例代码

void BubbleSort(int* arr, int n)
{
	for (int i = 0; i < n-1; i++)
	{
		int exchange = 0;
		for (int j = 0; j < n - i - 1; j++)
		{
			//升序
			if (arr[j] < arr[j + 1])
			{
				exchange = 1;
				Swap(&arr[j], &arr[j + 1]);
			}
		}
		if (exchange == 0)
		{
			break;
		}
	}
}

1.3 比较

直接插入排序与冒泡排序比较：

。与直接插入排序法相比，比较次数一致，但冒泡排序的交换需要执行三次，而直接插入排序因为使用了tmp临时变量存储要插入的数据，只用执行一次，所以直接插入排序法效率明显更高。与直接选择排序法相比，直接选择排序法无论数组是否有序都要执行到结束条件，不存在最好最坏时间复杂度。而冒泡排序因为使用了exchange变量进行优化，可以在最好时间复杂度上达到线性的结果。

2. 快速排序

快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序⽅法。

基本思想：

任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两⼦序列，左⼦序列中所有元素均⼩于基准值，右⼦序列中所有元素均⼤于基准值，然后最左右⼦序列重复该过程，直到所有元素都排列在相应位置上为⽌。

递归法实现快排：

快排主要主体框架
void QuickSort(int* arr, int left, int right) { if (left >= right) { return; } //[left,right]--->找基准值mid int keyi = _QuickSort(arr, left, right); //左子序列：[left,keyi-1] QuickSort(arr, left, keyi - 1); //右子序列：[keyi+1,right] QuickSort(arr, keyi + 1, right); }

快速排序重要步骤：找基准值

递归法如何找基准值？？？

。基准值左边元素都小于他，基准值右边元素都大于它，基准值所在的位置就是他应该所在位置

。再对该基准值所在左右子系列进行递归，如此往复，排序完成

2.1 递归版本实现快排

2.1.1 hoare版本

。第一个数默认为基准值

。定义左右指针

。left：从左往右找比基准值大的数据 right：从右往左找比基准值小的数据

。找到后将两个指针所对应的数据进行交换，right-- left++

。跳出循环后将基准值与right对应的位置进行交换

代码：

int _QuickSort1(int* arr, int left, int right)
{
	int keyi = left;
	++left;

	while (left <= right)//left和right相遇的位置的值比基准值要大
	{
		while (left <= right && arr[right] > arr[keyi])
		{·
			right--;
		}
		//right找到比基准值小/  等于？
		while (left <= right && arr[left] < arr[keyi])
		{
			left++;
		}
		//right left
		if (left <= right)
		{
			Swap(&arr[left++], &arr[right--]);
		}
	}
	//right keyi交换
	Swap(&arr[keyi], &arr[right]);

	return right;
}

问题：

1 上面的三个 "=" 可不可以去掉？？？

-> 先看while循环

示意图：

此时将right对应的数据与基准值交换显然不对。所以"="加上才正确。

上述两个内层循环相似，不再描述。

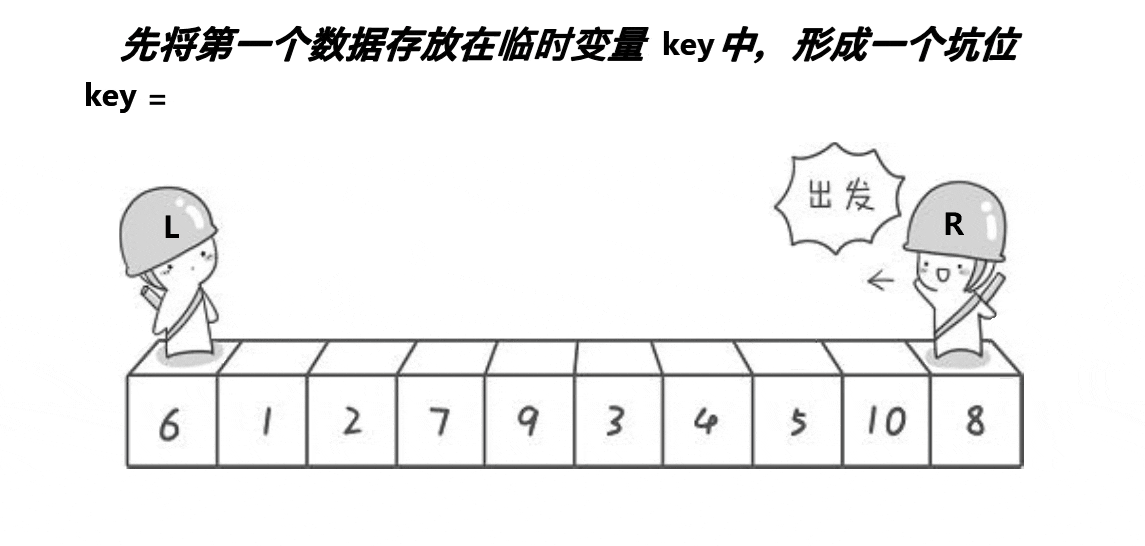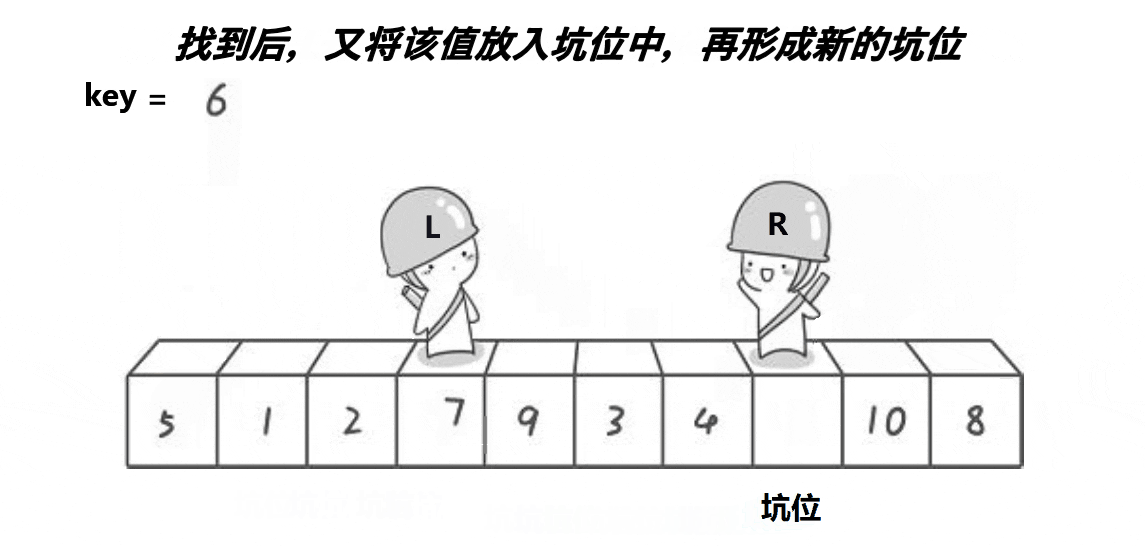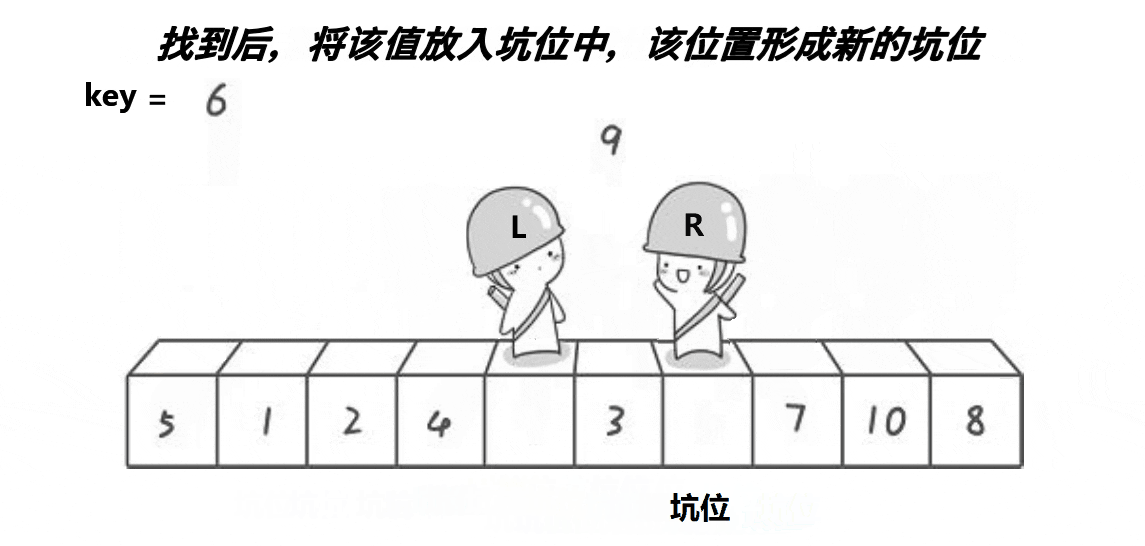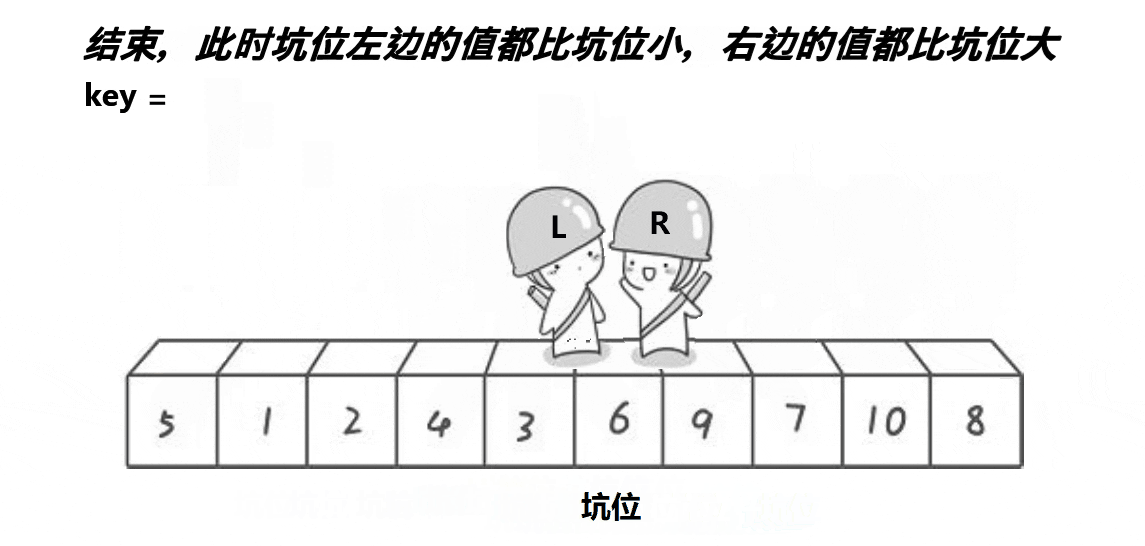
2.1.2 挖坑法

思路：

创建左右指针。⾸先从右向左找出⽐基准⼩的数据，找到后⽴即放⼊左边坑中，当前位置变为新的"坑"，然后从左向右找出⽐基准⼤的数据，找到后⽴即放⼊右边坑中，当前位置变为新的"坑"，结束循环后将最开始存储的分界值放⼊当前的"坑"中，返回当前"坑"下标（即分界值下标）

动图：

问题1：

left与right是否取等？？？

以上面动图为例，如果取等最后当left和right相遇时left还要++一次，导致hole所在位置偏移，发生错误，所以不取等

//挖坑法
int _QuickSort2(int* arr, int left, int right)
{
	int hole = left;
	int key = arr[hole];

	while (left < right)
	{
		while (left < right && arr[right] > key)
		{
			--right;
		}
		arr[hole] = arr[right];
		hole = right;
		while (left < right && arr[left] < key)
		{
			++left;
		}
		arr[hole] = arr[left];
		hole = left;
	}
	arr[hole] = key;
	return hole;
}

2.1.3 lomuto指针

思路：

创建前后指针，从左往右找⽐基准值⼩的进⾏交换，使得⼩的都排在基准值的左边

动图：

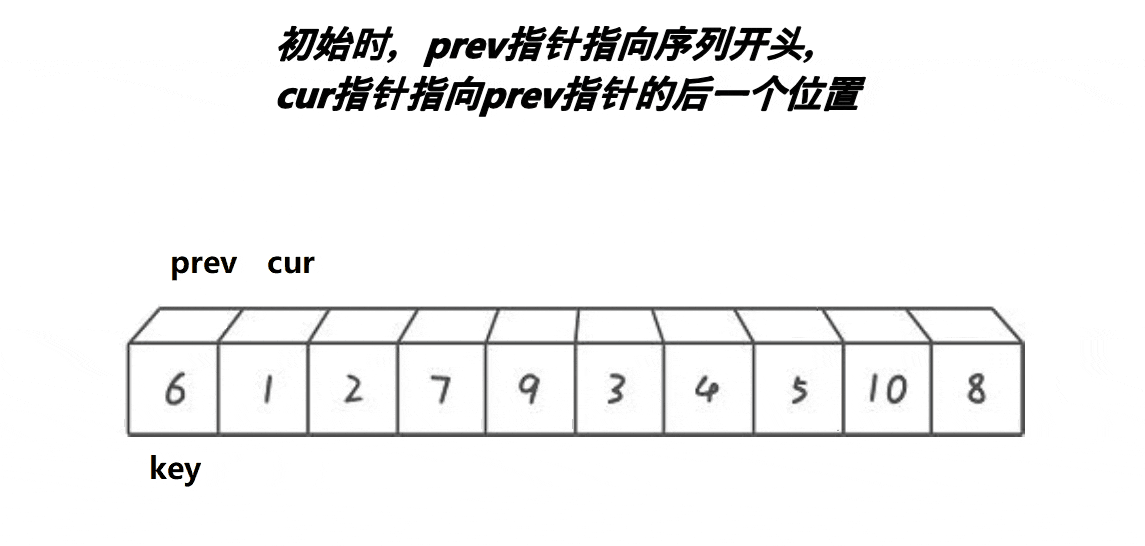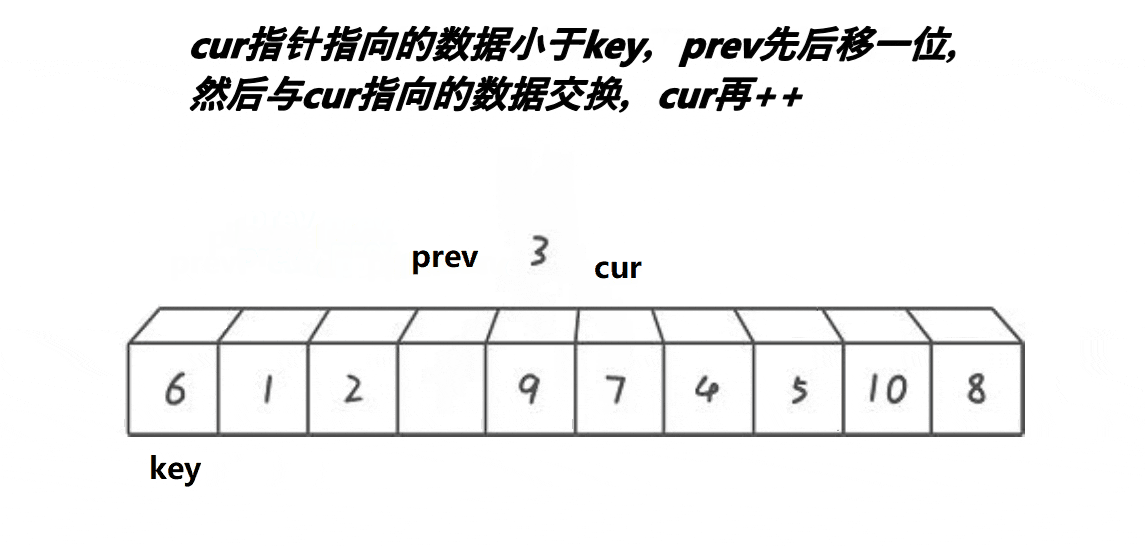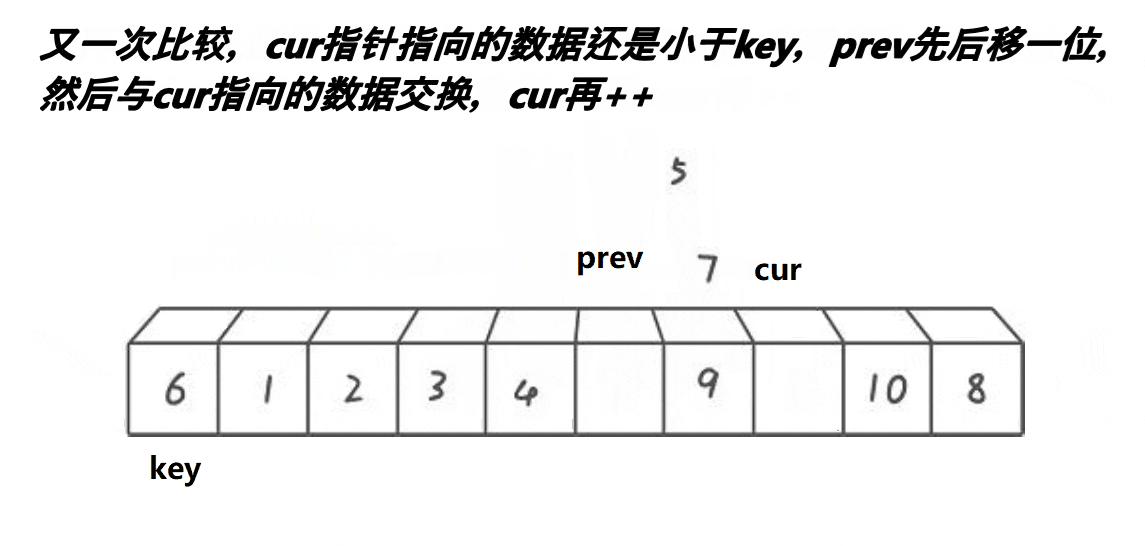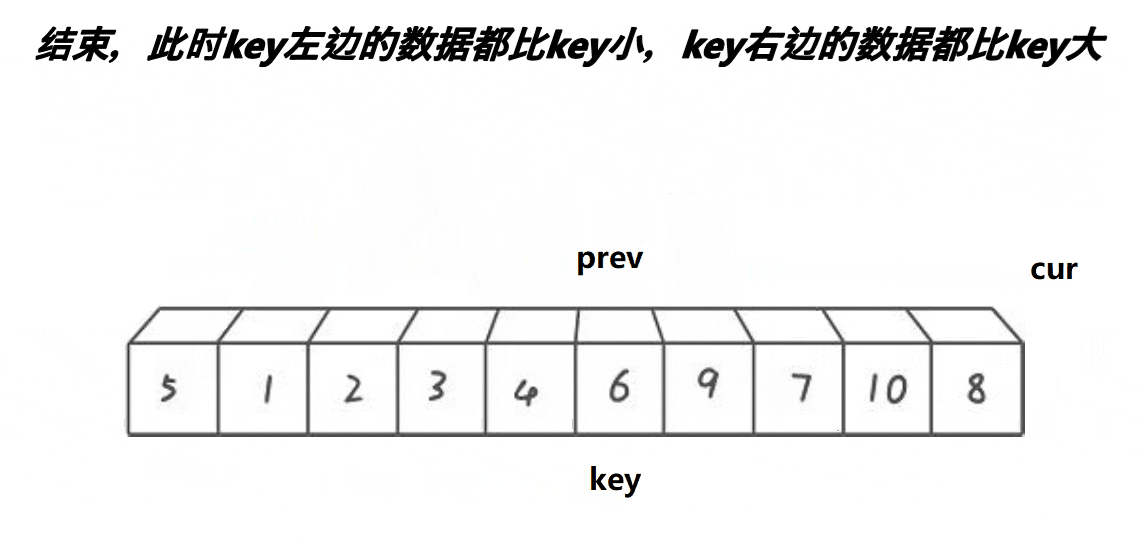
定义 prev，cur=prev+1；

如果cur指定数据比基准值小先让prev++，prev！=cur防止自身发生交换浪费时间，cur再++；

如果cur指定的数据比基准值大，则cur++，不再执行任何其它操作。

//lomuto前后指针法
int _QuickSort(int* arr, int left, int right)
{
	int prev = left, cur = left + 1;
	int keyi = left;
 
	while (cur <= right)
	{
		if (arr[cur] < arr[keyi] && ++prev != cur)
		{
			Swap(&arr[cur], &arr[prev]);
		}
		cur++;
	}
	Swap(&arr[keyi], &arr[prev]);
	return prev;
}

递归法复杂度分析时间复杂度：每一层的总时间复杂度都是O（n），因为需要对每一个元素遍历一次。而且在最好的情况下，同样也是有logn层，所以快速排序最好的时间复杂度为O（nlogn）。空间复杂度：二叉树递归最大深度为logn，即O（nlogn）以上是最好情况，最坏情况则是上面说的一次排序一个数据，时间复杂度O(n2)，空间复杂度O(n)。不过现实中基本不会出现这种情况。

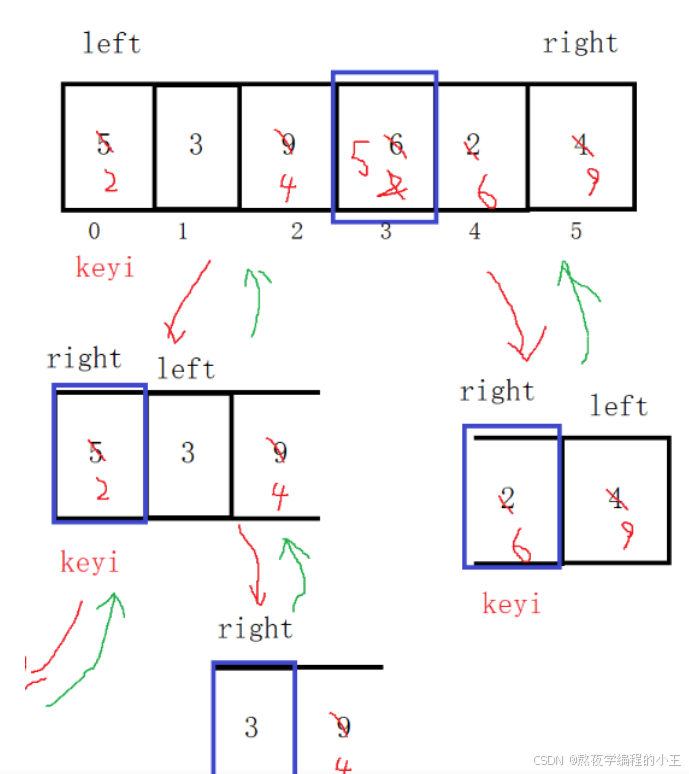
2.2 非递归实现快排

需要借助数据结构---> 栈

栈的博客：数据结构————栈的讲解(超详细！！！)-CSDN博客

栈是先进后出，所以插入先插入right后插入left
找基准值方法使用双指针法最简单
根据基准值划分左右区间
- 左区间：[begin,keyi-1]
- 右区间：[keyi+1,end]
循环直到栈为空

//非递归版本快排
//--借助数据结构--栈
void QuickSortNonR(int* arr, int left, int right)
{
	ST st;
	STInit(&st);
	StackPush(&st, right);
	StackPush(&st, left);

	while (!StackEmpty(&st))
	{
		//取栈顶元素---取两次
		int begin = StackTop(&st);
		StackPop(&st);

		int end = StackTop(&st);
		StackPop(&st);
		//[begin,end]---找基准值

		int prev = begin;
		int cur = begin + 1;
		int keyi = begin;

		while (cur <= end)
		{
			if (arr[cur] < arr[keyi] && ++prev != cur)
			{
				Swap(&arr[cur], &arr[prev]);
			}
			cur++;
		}
		Swap(&arr[keyi], &arr[prev]);

		keyi = prev;
		//根据基准值划分左右区间
		//左区间：[begin,keyi-1]
		//右区间：[keyi+1,end]
		
		if (keyi + 1 < end)
		{
			StackPush(&st, end);
			StackPush(&st, keyi + 1);
		}
		if (keyi - 1 > begin)
		{
			StackPush(&st, keyi - 1);
			StackPush(&st, begin);
		}
	}

	STDestroy(&st);
}