2024-12-16：使数组中所有元素相等的最小开销。用go语言，给定一个整数数组 nums 以及两个整数 cost1 和 co

福大大架构师每日一题

发布于 2024-12-19 18:42:09

13500

代码可运行

文章被收录于专栏：福大大架构师每日一题福大大架构师每日一题

运行总次数：0

代码可运行

2024-12-16：使数组中所有元素相等的最小开销。用go语言，给定一个整数数组 nums 以及两个整数 cost1 和 cost2，你可以进行以下两种操作多次：

1.选择数组中的某个元素的下标 i，将 nums[i] 增加 1，花费为 cost1。

2.同时选择数组中两个不同的下标 i 和 j，将 nums[i] 和 nums[j] 都增加 1，花费为 cost2。

你的目标是使数组中的所有元素相等，求达成此目标所需的最小总开销。由于结果可能很大，请将结果对 1000000007 取模后返回。

输入：nums = [4,1], cost1 = 5, cost2 = 2 。

输出：15 。

解释：

执行以下操作可以使数组中所有元素相等：

1.将 nums[1] 增加 1 ，开销为 5 ，nums 变为 [4,2] 。

2.将 nums[1] 增加 1 ，开销为 5 ，nums 变为 [4,3] 。

3.将 nums[1] 增加 1 ，开销为 5 ，nums 变为 [4,4] 。

总开销为 15 。

答案2024-12-16：

chatgpt[1]

题目来自leetcode3139。

大体步骤如下：

1.初始化变量 mod 为 1_000_000_007，表示取模值。

2.计算数组 nums 的长度 n，以及数组中的最小值 m 和最大值 M。

3.计算基准值 base，初始值为每个元素的和乘以最大值 M 减去所有元素的和，即 n*M - Σ(nums)。

4.检查特殊情况：若数组大小小于等于 2 或者 cost1 的两倍小于等于 cost2，则直接返回基准值乘以 cost1 取模后的结果。

5.定义函数 f(x)，根据提供的计算规则计算总开销。

6.计算一个关键值 i，根据给定的公式进行计算，用于确定最终结果在哪个范围内。

7.根据 i 和 M 的关系，选择合适的值来计算最小开销，并返回结果。

总体时间复杂度：

• 此算法的时间复杂度取决于遍历数组和执行各种计算操作，为 O(n)。

总体额外空间复杂度：

• 算法中使用了一些常量空间来存储变量和常量值，以及 map 数据结构用于存储计数，因此额外空间复杂度为 O(1)。

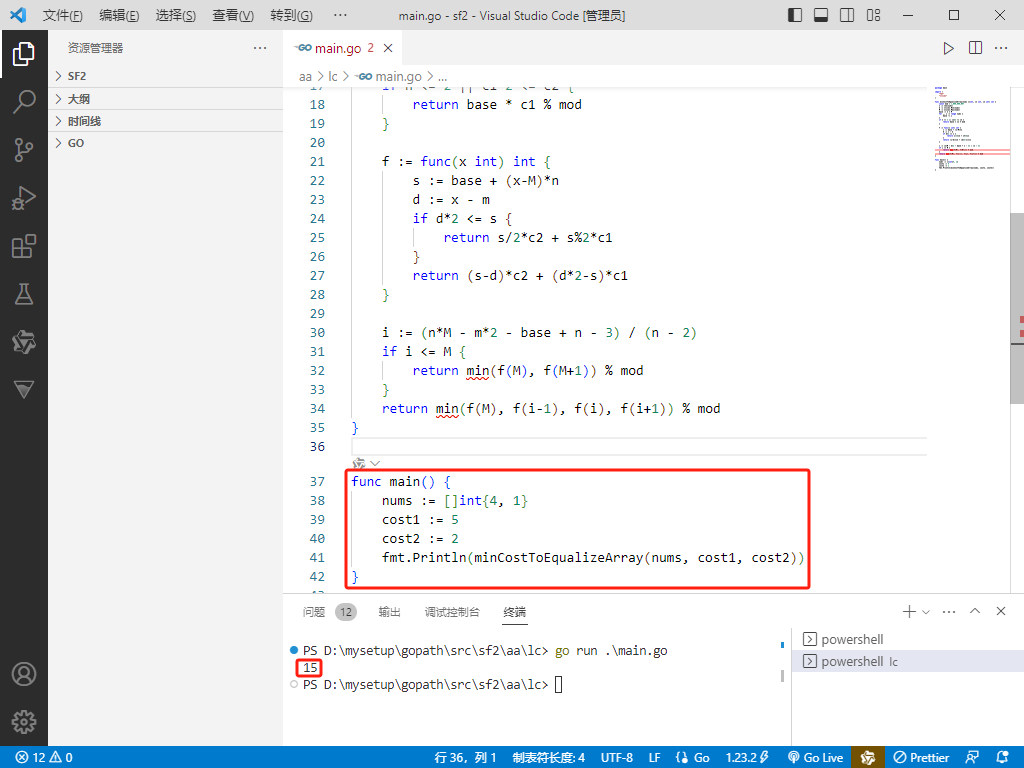
Go完整代码如下：

package main

import(
"fmt"
"slices"
)

func minCostToEqualizeArray(nums []int, c1 int, c2 int)int{
const mod =1_000_000_007
    n :=len(nums)
    m := slices.Min(nums)
    M := slices.Max(nums)
base:= n * M
for _, x :=range nums {
base-= x
}
if n <=2|| c1*2<= c2 {
returnbase* c1 % mod
}

    f :=func(x int)int{
        s :=base+(x-M)*n
        d := x - m
if d*2<= s {
return s/2*c2 + s%2*c1
}
return(s-d)*c2 +(d*2-s)*c1
}

    i :=(n*M - m*2-base+ n -3)/(n -2)
if i <= M {
return min(f(M), f(M+1))% mod
}
return min(f(M), f(i-1), f(i), f(i+1))% mod
}

func main(){
    nums :=[]int{4,1}
    cost1 :=5
    cost2 :=2
    fmt.Println(minCostToEqualizeArray(nums, cost1, cost2))
}

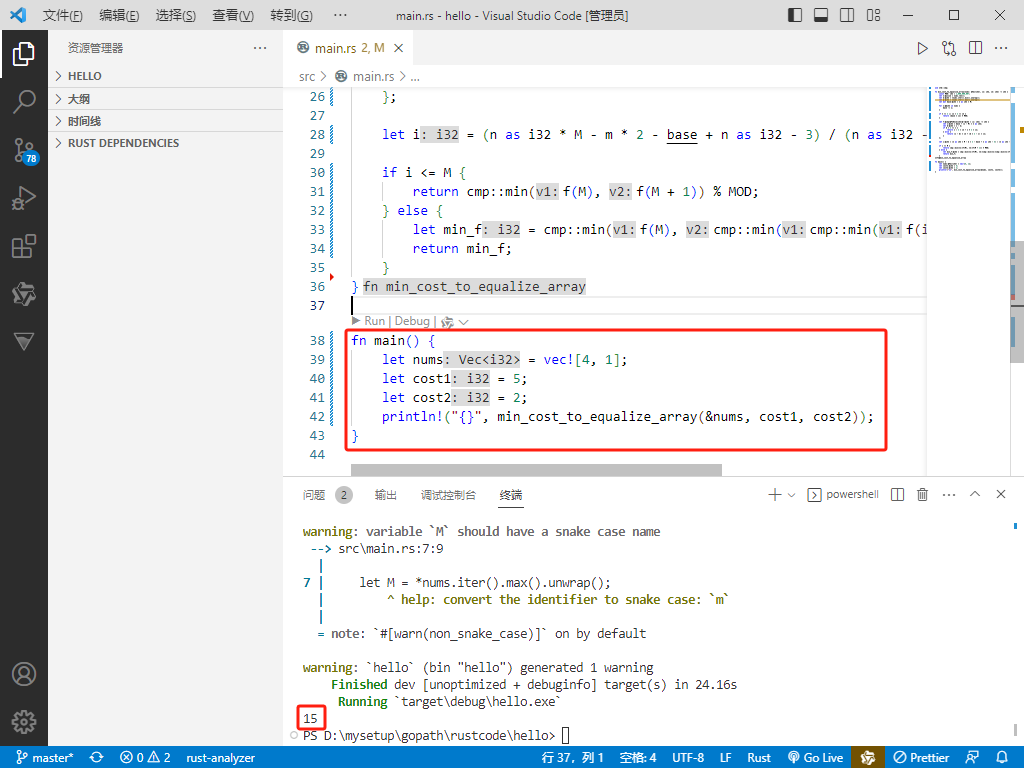
Rust完整代码如下：

use std::cmp;

fnmin_cost_to_equalize_array(nums:&Vec<i32>, c1:i32, c2:i32)->i32{
const MOD:i32=1_000_000_007;
letn= nums.len();
letm=*nums.iter().min().unwrap();
letM=*nums.iter().max().unwrap();
letmut base= n asi32* M;

forxin nums {
        base -= x;
}

if n <=2|| c1 *2<= c2 {
return(base * c1)% MOD;
}

letf=|x:i32|->i32{
lets= base +(x - M)* n asi32;
letd= x - m;
if d *2<= s {
return s /2* c2 + s %2* c1;
}else{
return(s - d)* c2 +(d *2- s)* c1;
}
};

leti=(n asi32* M - m *2- base + n asi32-3)/(n asi32-2);

if i <= M {
return cmp::min(f(M),f(M +1))% MOD;
}else{
letmin_f= cmp::min(f(M), cmp::min(cmp::min(f(i -1),f(i)),f(i +1)))% MOD;
return min_f;
}
}

fnmain(){
letnums=vec![4,1];
letcost1=5;
letcost2=2;
println!("{}",min_cost_to_equalize_array(&nums, cost1, cost2));
}