数据小白必看:七大排序算法超详细讲解(上)
一、排序
1.排序的概念
排序:将一组数据进行按照特定的顺序(如升序或者降序)进行排列的操作。
- 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,在排完序列后,r[i]仍在r[j]之前。这种排序叫做稳定的,否则为不稳定。
例如:

第1个3是在第二个3之前,排序后,两个位置发生前后变化,这种是不稳定性。如果前后排序没有发生变化那么是稳定性。
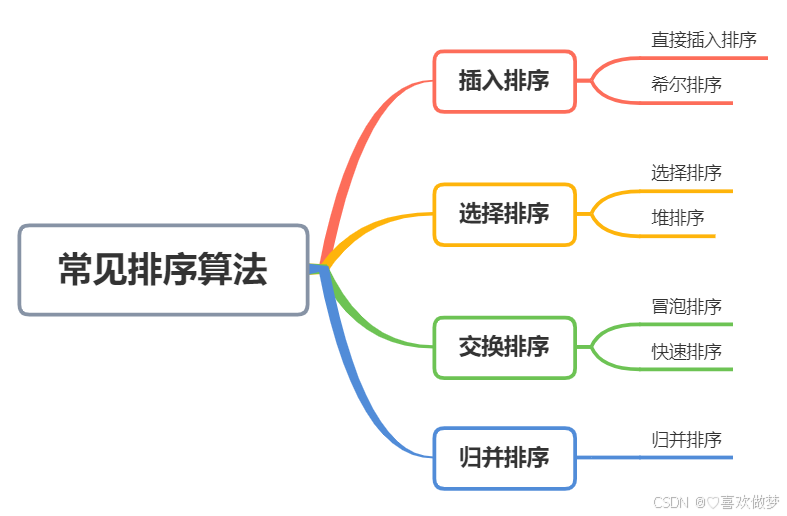
2.常见的排序算法
二、插入排序
1.直接插入排序
基本思想
基本思想:把待排序的元素插入到已经排序好的部分序列中合适的位置,直到全部元素都排序好。例如:我们在整理手中的扑克牌的时候,我们将拿到的牌,将其插入前面排中合适的位置。
实现过程



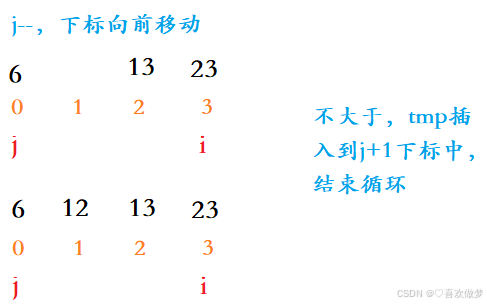
以上有部分步骤省略,但影响不大
思路:
- i从1下标开始遍历,j从i-1开始;
- 将下标i中的元素给tmp;
- 将j下标的元素与tmp中的元素进行比较: 如果j中的元素大于tmp中的元素,那么将j中的元素放到j+1的元素中 如果j中的元素小于tmp中的元素,那么说明j+1是适合tmp元素的位置,将其插入,退出循环
代码:
public static void insertSort(int[] array){
for (int i = 1; i < array.length; i++) {
//将下标i中的元素给tmp;
int tmp=array[i];
int j = i-1;
for (; j >=0; j--) {
//将j中的元素与tmp中的元素进行比较
//如果j中的元素大于tmp中的元素,那么将j中的元素放到j+1的元素中
if(tmp<array[j]){
array[j+1]=array[j];
}else{
//否则说明j+1是适合tmp元素的位置,将其插入
array[j+1]=tmp;
break;
}
}
array[j+1]=tmp;
}
}可能会有的疑问:
1.为什么j的循环之后,还有写array[j+1]=tmp?

将j的下标中的元素给到j+1中,随后j--,这个时候j<0,不满足循环条件,那么退出循环,这个时候如果不在i循环中加array[j+1]=tmp。那么结果就只有13 13 23 12.没有将tmp插入到合适的位置中
2.为什么是将j下标的元素给j+1,而不是给i下标,j+1的元素不就是i下标的元素吗?

在起始i的时候,执行j循环的时候,确实j+1下标,但是在每次指向完一次j的循环,j的下标就向前移动,而在j移动的过程中i是不变的。
3.为什么j要--,看图中好像我只要把前后两个元素进行笔记不就好了吗?

在比较过程中,可以算是每次从该位置,从后开始比较,如果两个位置前后大小交换,那么在交换的元素的前后位置可能也要发生交换。
- 空间复杂度:O(1)
- 时间复杂度:O(N^2) 最坏的情况下:逆序; 最好的情况下:本身有序,越有序越快
- 稳定性:稳定的排序
2.希尔排序(缩小增量排序)
基本思想
基本思想:先将整个待排序的数据元素,分成若干个组,并对每一组的元素进行排序。这些子序列的元素一开始间隔相对较大,随后逐步缩小间隔,继续进行插入排序,直到这个间隔=1时,所有元素在一组内在进行排序。
实现过程
除了在分组与直接插入排序的思想不同,但在排序的思想与直接插入排序的思想基本相同
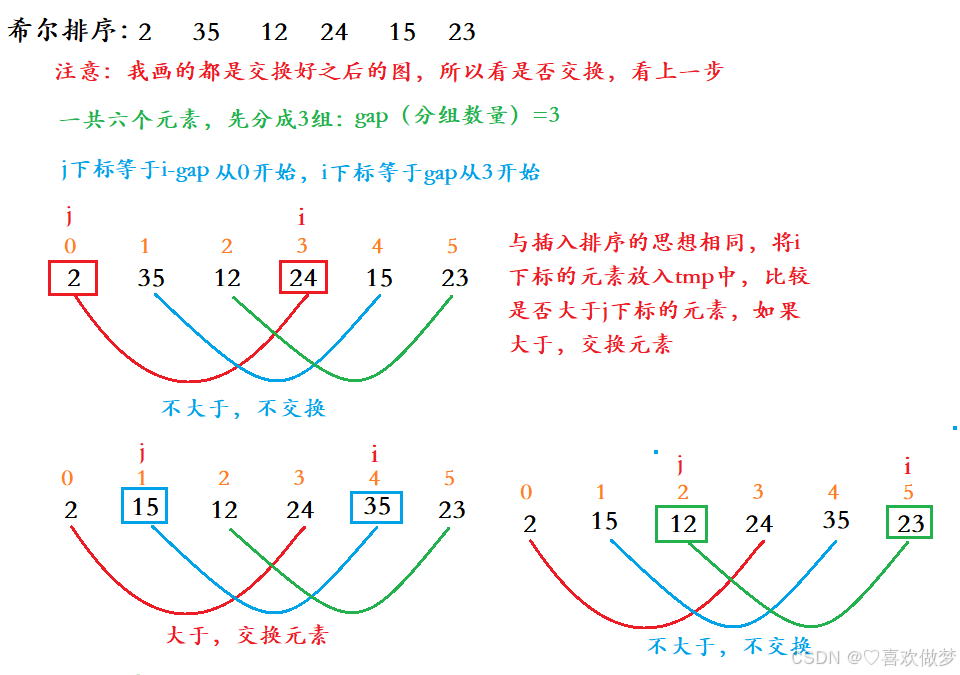
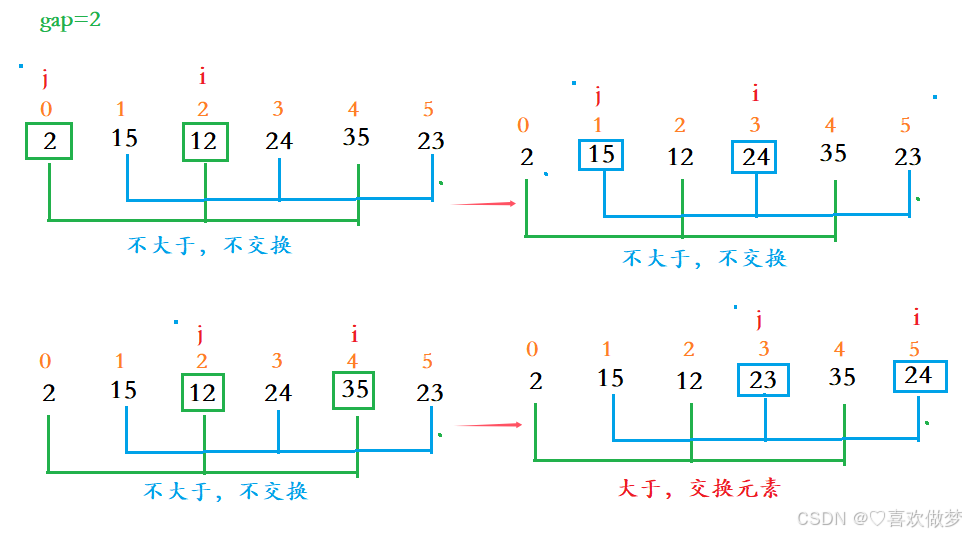
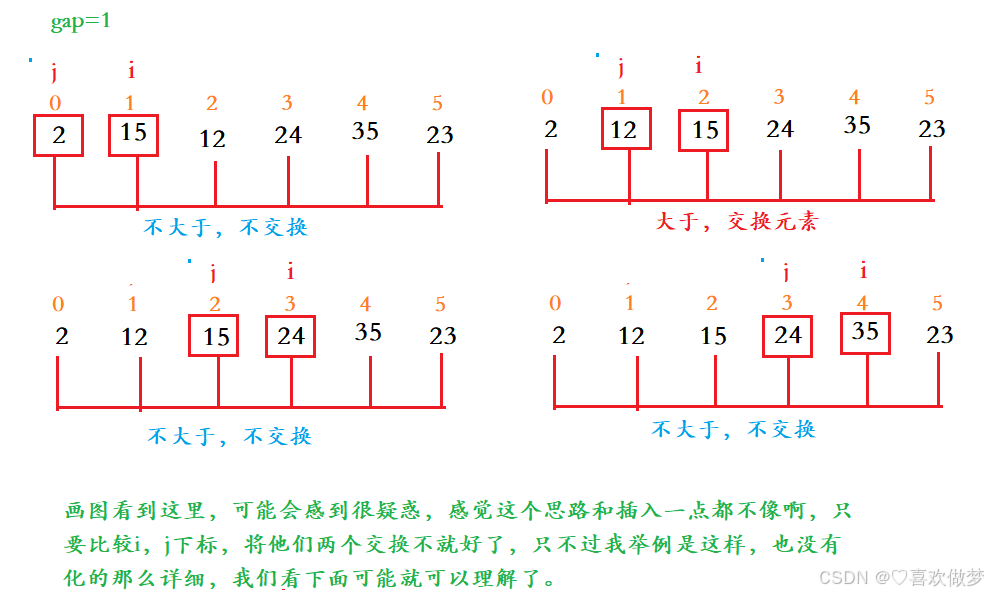
以上有省略部分步骤,影响不大
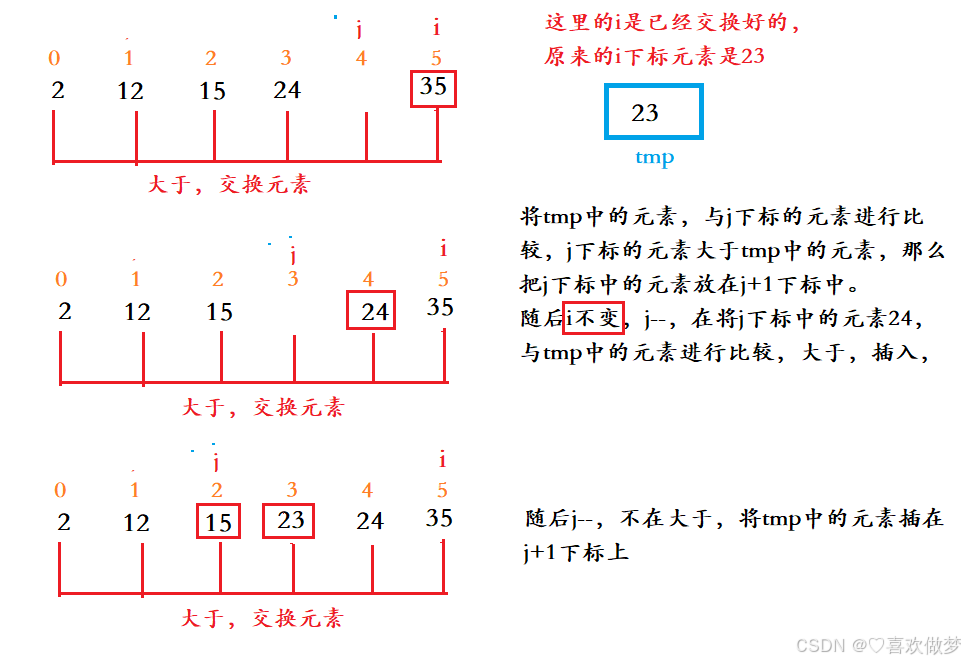
思路:
- 分组:gap=gap/2,直到gap小于1不在排序
- 排序:
- i从gap下标开始遍历,j从i-gap开始;
- 将下标i中的元素给tmp;
- 将j下标的元素与tmp中的元素进行比较: 如果j中的元素大于tmp中的元素,那么将j中的元素放到j+gap的元素中 如果j中的元素小于tmp中的元素,那么说明j+gap是适合tmp元素的位置,将其插入,退出循环
细心的同学可以发现,其实思路只是把直接插入排序的1改成了gap;
代码:
public static void shellSort(int[] array){
int gap=array.length;
while(gap>=1){
gap=gap/2;
//gap=gap/3+1;
shell(array,gap);
}
}
public static void shell(int[] array,int gap){
for (int i =gap; i < array.length; i++) {
//将下标i中的元素给tmp;
int tmp=array[i];
int j = i-gap;
for (; j >=0; j-=gap) {
//将j中的元素与tmp中的元素进行比较
//如果j中的元素大于tmp中的元素,那么将j中的元素放到j+1的元素中
if(tmp<array[j]){
array[j+gap]=array[j];
}else{
//否则说明j+1是适合tmp元素的位置,将其插入
array[j+gap]=tmp;
break;
}
}
array[j+gap]=tmp;
}
}可能会有的疑问:
不是说就是将直接插入排序中的1改成gap吗?为什么i是++,而不是加gap?
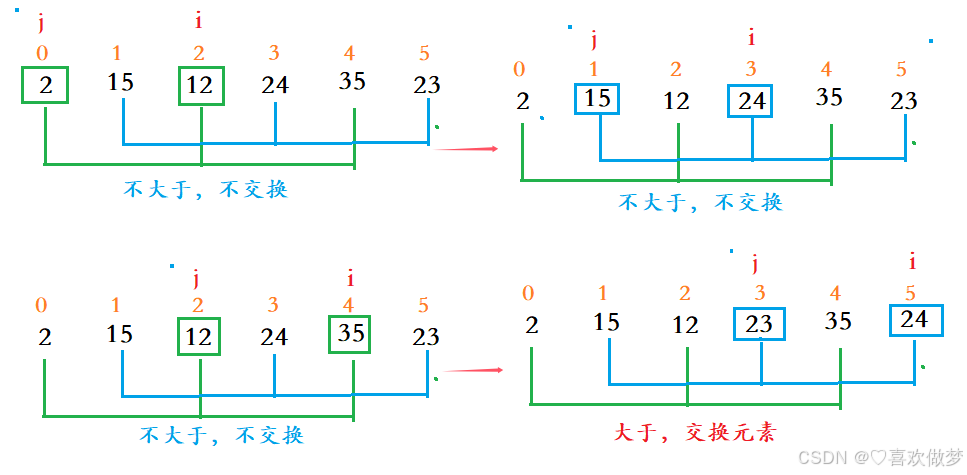
仔细看上面的图,我的箭头是向右的,而不是向下的。因为虽然他分组了,但是每一组的元素还是要遍历进行交换的,所以是i++。
- 希尔排序是对直接插入排序的优化;
- 稳定性:不稳定;
- 时间复杂度:n^1.3~n^1.5;
- 空间复杂度:O(1);
三、选择排序
1.选择排序
基本思想
基本思想:每一次从待排序的序列中找到最小(大)的元素,存放到排序序列中的起始位置,以此类推,直到全部待排序的数据元素排完。
方法1
实现过程:
纠错:以下图片mid为min

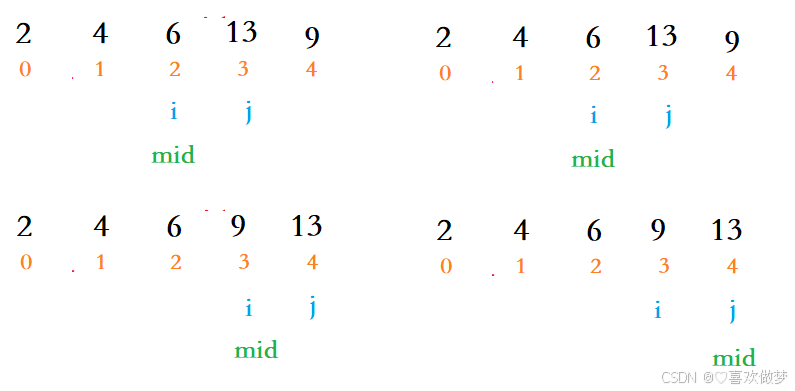
思路
- i从头开始遍历,minIndex的起始位置从i开始;
- j=i+1开始向后与minIndex中的元素进行比较,寻找当前最小的元素,记录最小元素下标到minIndex;
- 将i位置的元素与minIndex的元素进行交换。
代码
public static void selectSort(int[] array){
for (int i = 0; i < array.length; i++) {
//记录最小元素下标
int minIndex=i;
for (int j=i+1; j < array.length ; j++) {
//如果j下标的元素比mid的元素小,将j下标赋值给mid
if(array[j]<array[minIndex]){
minIndex=j;
}
}
//将i下标与当前的最小值进行交换
swap(array,i,minIndex);
}
}
public static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}方法2
思路:
- 设立left和right两个指针来确定数组区间,left从0开始向后移动,right从array.length-1向前移动,直到left大于等于right排序
- 初始化minIndex和maxIndex为left,i下标从left+1开始,将i下标的元素分别与minIndex中的元素和maxIndex进行比较,寻找当前的最小值与最大值。
- 每轮寻找完,将最小值与left下标进行交换,最大值与right进行交换,随后left向后移动,right向前移动
实现过程:
纠错:以下图片mid为min

代码
public static void selectSort2(int[] array){
int left=0;
int right= array.length-1;
while(left<right){
int minIndex=left;
int maxIndex=left;
for (int i = left+1; i <=right ; i++) {
if(array[i]>array[maxIndex]){
maxIndex=i;
}
if(array[i]<array[minIndex]){
minIndex=i;
}
}
swap(array,left,minIndex);
if(maxIndex==left){
maxIndex=minIndex;
}
swap(array,right,maxIndex);
left++;
right--;
}
}
public static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}可能会有的疑问:
为什么还要加下面这个代码?有什么用?

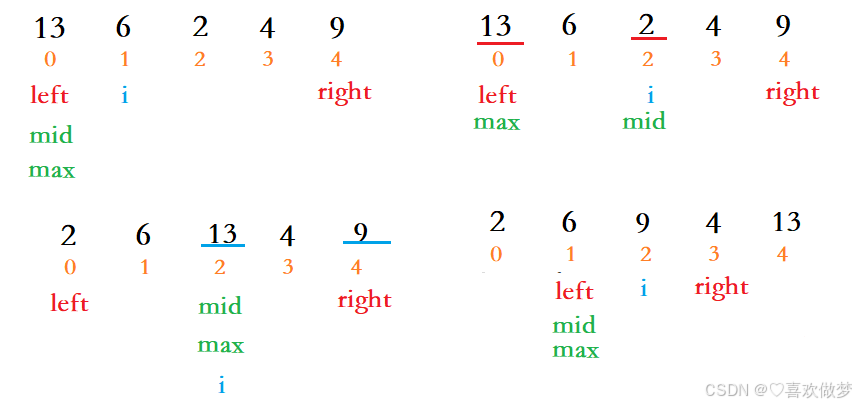
看上面的图,在left位置的时候,maxIndex已经是最大值的下标,在minIndex找到最小值的下标的时候,会将最小值与left位置进行交换,如果没有该代码,那么与maxIndex与right交换的元素,是交换后的最小值,而最大值被交换到原本最小值的位置,也就是minIndex。
- 直接选择排序效率不高,用的少;
- 稳定性:不稳定;
- 时间复杂度:O(n^2);
- 空间复杂度:O(1);
2.堆排序
基本思想
基本思想:堆排序是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择排序。需要注意的是排升序要建立大堆,排降序要建立小堆。
堆排序的思路和图我就不在说啦,如果想看的话可以看我上一篇还在死磕算法?懂“堆”与“优先级队列”,代码效率飙升 中有写到堆排序
public void heapSort(){
int end=usedSize-1;
while(end>0) {
swap(elem, 0, end);
siftDown1(0,end);
end--;
}- 效率会高一些;
- 稳定性:不稳定;
- 时间复杂度:O(n*
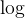
\log
N) ;
- 空间复杂度:O(1);
这篇博客就到这里啦,其他排序内容有点多,我下篇在写,感谢支持🌹🌹🌹
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2024-12-21,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

