如何在AVL树中高效插入并保持平衡:一步步掌握旋转与平衡因子 —— 平衡因子以及AVL结构篇
如何在AVL树中高效插入并保持平衡:一步步掌握旋转与平衡因子 —— 平衡因子以及AVL结构篇
用户11286421
发布于 2025-03-16 20:37:17
发布于 2025-03-16 20:37:17
代码可运行
运行总次数:0
代码可运行
AVL树的概念
AVL树(Adelson-Velsky and Landis Tree)是一种自平衡二叉查找树,它的特点是每个节点的左子树和右子树的高度差不能超过1。这意味着AVL树是一种平衡的二叉树,通过保持树的平衡来保证查找操作的时间复杂度为O(log n),从而提高性能。
AVL树当中,重要的一个概念:
- 平衡因子(Balance Factor, BF): 每个节点都有一个平衡因子,定义为节点的左子树高度减去右子树高度。(当然,右子树的高度减去左子树的高度也是可以的)平衡因子的值只能是-1、0或1。
- 今天这篇文章,作者定义的平衡因子是 bf = rh(right height) - lh(left height);即选择右子树高度减去左子树高度
AVL树的结构
template<class K, class V>
struct AVLTreeNode
{
// 每个节点包含的元素和指针
pair<K, V> _kv; // 存储键值对
AVLTreeNode<K, V>* _left; // 左子树指针
AVLTreeNode<K, V>* _right; // 右子树指针
AVLTreeNode<K, V>* _parent; // 父节点指针
int _bf; // 平衡因子
// 构造函数
AVLTreeNode(const pair<K, V>& kv)
: _kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0)
{}
};
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node; // 节点类型
public:
// 其他操作(插入、删除、查找等)可以在此添加
// 旋转
/**/ 旋转的详细讲解在下一篇文章,有兴趣的读者可以前往下一篇进行查看**
private:
Node* _root; // 根节点指针
};AVL树的插入
重点关注如何在插入时保持树的平衡。
插入操作概述 AVL树插入操作的过程与普通的二叉搜索树插入过程相似,唯一不同的是,AVL树在插入节点后需要检查树的平衡性,并进行必要的旋转操作来保持平衡。我们可以将插入操作分为几个步骤:
- 二叉搜索树的插入:按照二叉搜索树的规则插入节点。
- 更新节点高度:插入节点后,需要更新沿路径的所有节点的高度。
- 检查平衡因子:检查每个节点的平衡因子,确定是否需要进行旋转。
- 旋转操作:如果某个节点的平衡因子不在-1, 0, 1范围内,进行旋转以恢复平衡。
平衡因子更新终止条件
- 更新后parent的平衡因⼦等于0,更新中parent的平衡因⼦变化为-1->0或者1->0,说明更新前parent⼦树⼀边⾼⼀边低,新增的结点插⼊在低的那边,插⼊后parent所在的⼦树⾼度不变,不会影响parent的⽗亲结点的平衡因⼦,更新结束。
- 更新后parent的平衡因⼦等于1或 -1,更新前更新中parent的平衡因⼦变化为0->1或者0->-1,说明更新前parent⼦树两边⼀样⾼,新增的插⼊结点后,parent所在的⼦树⼀边⾼⼀边低,parent所在的⼦树符合平衡要求,但是⾼度增加了1,会影响arent的⽗亲结点的平衡因⼦,所以要继续向上更新。
- 更新后parent的平衡因⼦等于2 或 -2,更新前更新中parent的平衡因⼦变化为1->2 或者 -1->-2,说明更新前parent⼦树⼀边⾼⼀边低,新增的插⼊结点在⾼的那边,parent所在的⼦树⾼的那边更⾼了,破坏了平衡,parent所在的⼦树不符合平衡要求,需要旋转处理,旋转的⽬标有两个:1、把parent⼦树旋转平衡。2、降低parent⼦树的⾼度,恢复到插⼊结点以前的⾼度。所以旋转后也不需要继续往上更新,插⼊结束。
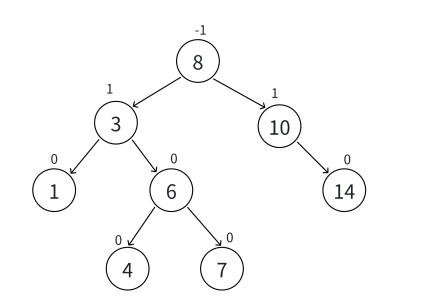
平衡因子更新的3种情况。
更新到10结点,平衡因⼦为2,10所在的⼦树已经不平衡,需要旋转处理
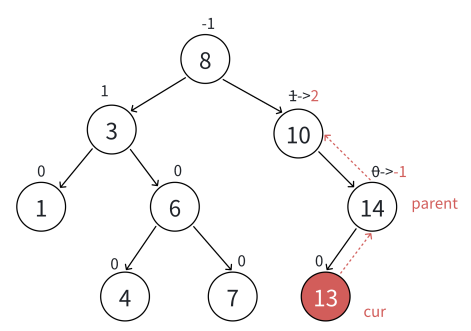
更新到中间结点,3为根的⼦树⾼度不变,不会影响上⼀层,更新结束

最坏更新到根停⽌
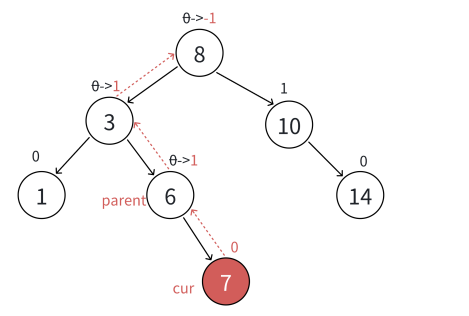
插入以及平衡因子的保持
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node<K, V>(kv);
return true;
}
Node<K, V>* parent = nullptr;
Node<K, V>* cur = _root;
// 寻找插入位置
while (cur)
{
parent = cur;
if (kv.first < cur->_kv.first)
{
cur = cur->_left;
}
else if (kv.first > cur->_kv.first)
{
cur = cur->_right;
}
else
{
return false; // 键值已存在
}
}
// 创建新的节点并连接到父节点
cur = new Node<K, V>(kv);
if (kv.first < parent->_kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
// 更新平衡因子并处理不平衡
while (parent)
{
if (cur == parent->_left)
{
parent->_bf--; // 左子树高,平衡因子减1
}
else
{
parent->_bf++; // 右子树高,平衡因子加1
}
//平衡因子 = 右子树 - 左子树
// 如果平衡因子为0,结束更新
if (parent->_bf == 0)
{
break;
}
// 如果平衡因子为±1,继续向上更新
if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
// 如果平衡因子为±2,说明不平衡,进行旋转处理
else if (parent->_bf == 2 || parent->_bf == -2)
{
// 旋转处理
/**/ 旋转的详细讲解在下一篇文章,有兴趣的读者可以前往下一篇进行查看**
if (parent->_bf == -2 && cur->_bf == -1)//左高(在左子树)——右旋
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == 1)//右高(在左子树)——左旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)//左高(在右子树)——左右旋
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)//右高(在左子树)——右左旋
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else
{
assert(false); // 应该不会发生
}
}
return true;
}AVL树的查找
⼆叉搜索树逻辑实现即可,搜索效率为 O(logN)
Node* Find(const K& key)
{
// 从根节点开始查找
Node* cur = _root;
// 遍历树,直到找到目标节点或到达空节点
while (cur)
{
// 如果当前节点的键小于目标键,向右子树查找
if (cur->_kv.first < key)
{
cur = cur->_right;
}
// 如果当前节点的键大于目标键,向左子树查找
else if (cur->_kv.first > key)
{
cur = cur->_left;
}
// 如果当前节点的键等于目标键,返回当前节点
else
{
return cur;
}
}
// 如果遍历结束仍未找到目标节点,返回 nullptr
return nullptr;
}本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-03-15,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

