题目练习之位运算
前置知识(常见操作)
在正式开始题目练习之前,除了前面博客里面说到的基础知识,我们还需要找到一些常见操作~
1. 基础位运算
- 与运算 (&)(有0就是0)
- 示例:
0 & 0 = 0,0 & 1 = 0,1 & 0 = 0,1 & 1 = 1 - 解释:对应位都为1时结果为1,否则为0。
- 示例:
- 或运算 (|)(有1就是1)
- 示例:
0 | 0 = 0,0 | 1 = 1,1 | 0 = 1,1 | 1 = 1 - 解释:对应位有一个为1时结果为1。
- 示例:
- 异或运算 (^)(无进位相加)
- 示例:
0 ^ 0 = 0,0 ^ 1 = 1,1 ^ 0 = 1,1 ^ 1 = 0 - 解释:对应位不同结果为1,相同为0。
- 示例:
- 取反运算 (~):
- 示例:
~0 = 1,~1 = 0 - 解释:0变1,1变0。
- 示例:
接下来,常见操作第k/x位都是指的是从后面往前面数的第k/x位
2. 给定一个数n,确定它的二进制表示中的第k位是0还是1
- 方法:
(n >> k) & 1- 解释:将n右移k位,然后与1进行与运算,判断最低位是0还是1。
举例:

3. 将一个数n的二进制表示的第k位从0变成1,或从1变成0
- 方法:
n = n ^ (1 << k)- 解释:将1左移k位,然后与n进行异或运算,翻转第k位。
举例:


将一个数n的二进制表示的第k位修改为1
前面的操作就是直接变成相反的,如果我们现在想要把第k位修改为1,它可能最开始是1,就不需要变化了,如果最开始为0,我们把它变成1~
方法:n = n | (1 << k)
举例:


将一个数n的二进制表示的第k位修改为0
方法:n = n & (~(1<<x))
举例:

4. 将一个数n的二进制表示的前k位改成1
- 方法:n
= n | ((1 << k) - 1)- 解释:将1左移k位后减1,得到前k位全为1的数,然后与n进行或运算。
举例:

5. 将一个数n的二进制表示的前k位改成0
- 方法:n =
n & ~((1 << k) - 1)- 解释:将1左移k位后减1,取反后得到前k位全为0的数,然后与n进行与运算。
举例:

6. 提取一个数n的二进制表示中最右边的1
- 方法:
n & -n或n & (~n + 1)- 解释:取反后加1得到补码,与原数进行与运算,提取最右边的1。
举例:

7. 去掉一个数n的二进制表示中最右边的1
- 方法:
n & (n - 1)- 解释:将n减1后与原数进行与运算,去掉最右边的1。
举例:

8. 位运算的优先级
- 位运算的优先级低于算术运算,但高于逻辑运算。
- 示例:
a ^ b & c等价于a ^ (b & c)
技巧:不知道优先级,能加括号加括号
9. 异或运算小技巧
a ^ 0 = aa ^ a = 0a ^ b ^ c = a ^ c ^ b(交换律)
知道了这些常见操作,接下来我们就使用位运算来解决我们的算法问题~
只出现一次的数字
这个题目就比较简单了~
思路:所有数据进行异或,根据a^a=0,a^0=a,可以得到所有数据进行异或的结果就是我们想要的数据~
代码:
class Solution
{
public:
int singleNumber(vector<int>& nums)
{
int ret=0;
//所有数据进行异或
for(auto e:nums)
{
ret^=e;
}
return ret;
}
};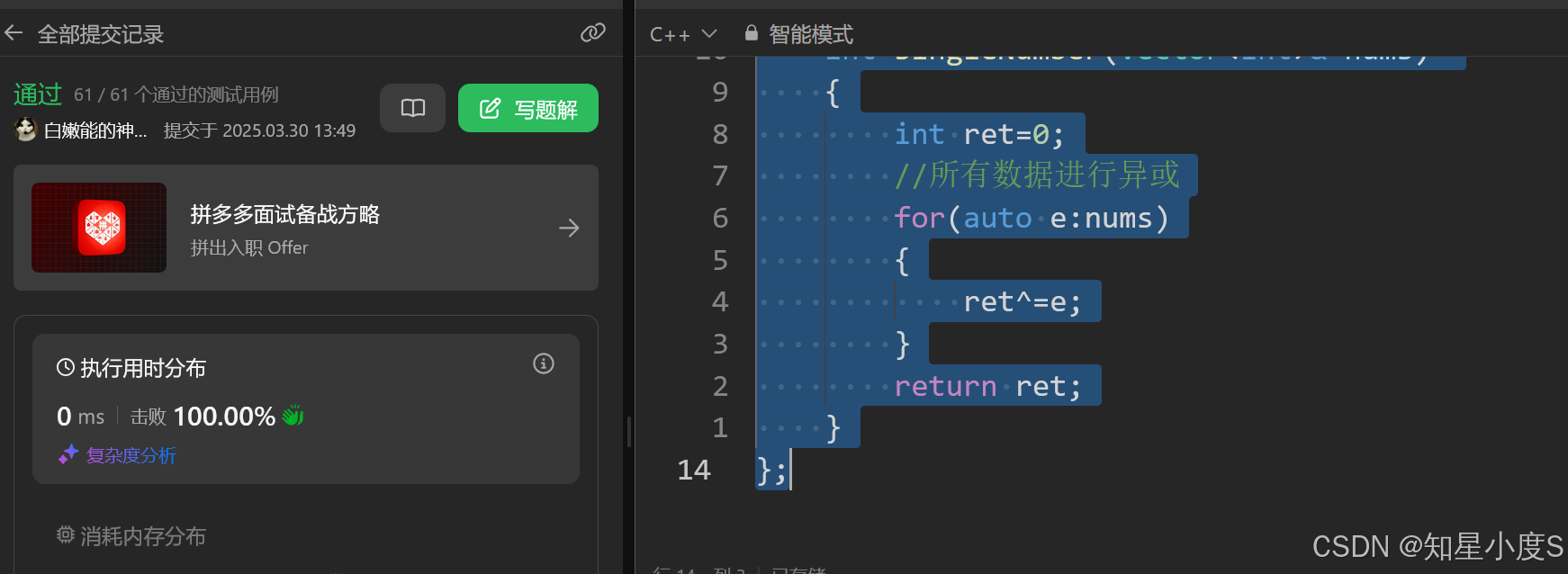
顺利通过~
丢失的数字
这个题目也比较简单,这些数是连续的,那么我们就可以利用数学里面的等差数列求和公式得到它本来的和,再减去已经存在的数据,就可以得到没有存在的数据~
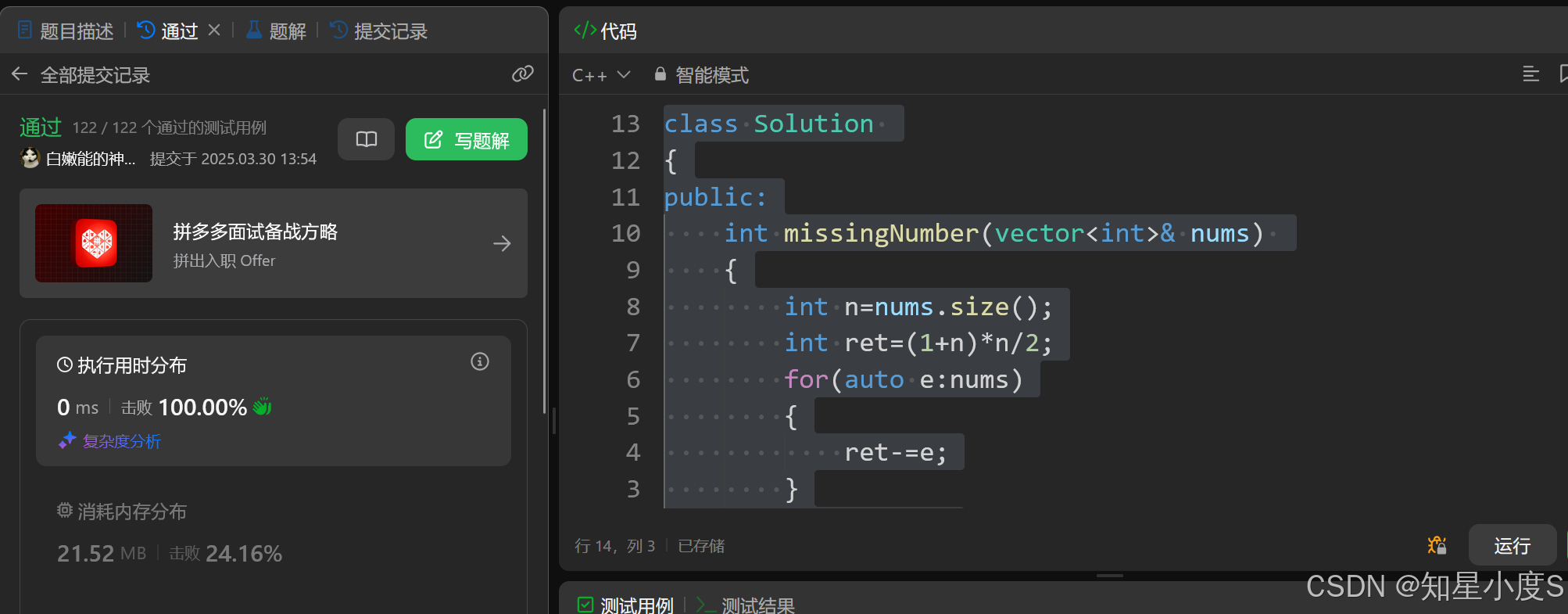
思路1:等差数列求和
代码:
class Solution
{
public:
int missingNumber(vector<int>& nums)
{
int n=nums.size();
int ret=(1+n)*n/2;
for(auto e:nums)
{
ret-=e;
}
return ret;
}
};
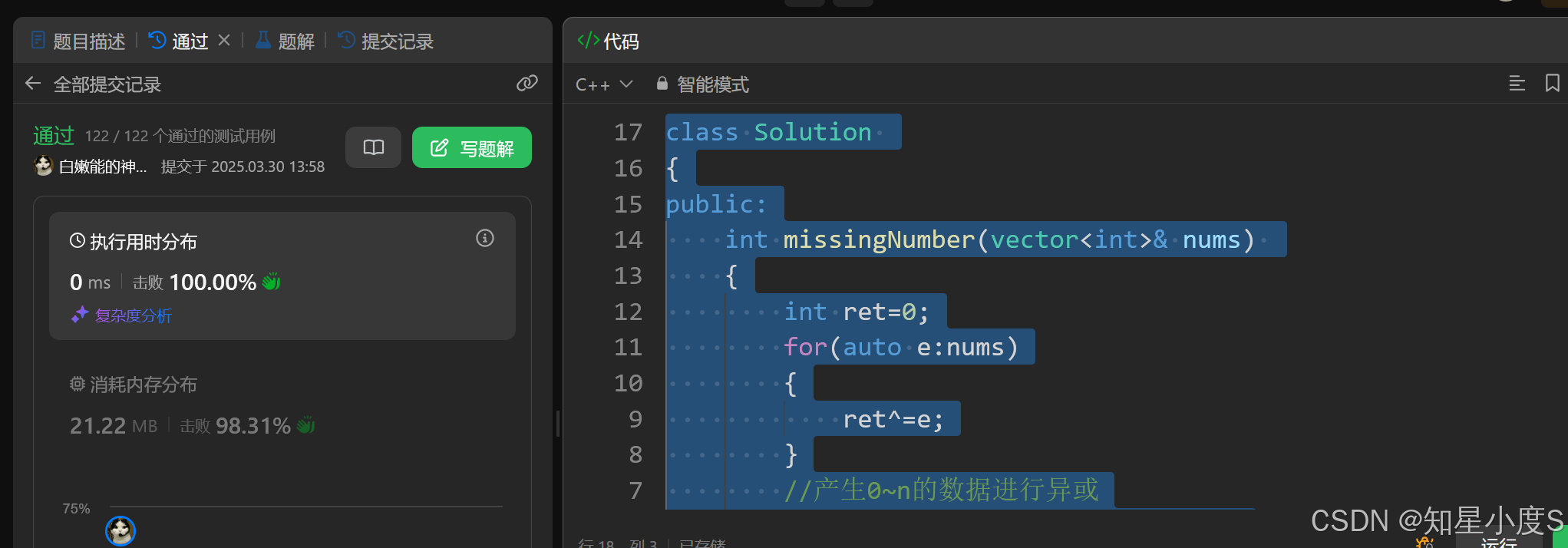
思路2:使用位运算,得到0~n的数据,与原来的数组元素进行异或,结果就是原来数组没有存在的数据~
代码:
class Solution
{
public:
int missingNumber(vector<int>& nums)
{
int ret=0;
for(auto e:nums)
{
ret^=e;
}
//产生0~n的数据进行异或
for(int i=0;i<=nums.size();i++)
{
ret^=i;
}
return ret;
}
};
两整数之和
可能一看这个题目挺简单的,但是不可以使用+,-符号啊,不过有一种投机取巧的方法就是直接return a+b;
也是可以通过的,当然这肯定是不太正确的解法,接下来我们使用位运算来解决这个问题~
加法最重要的就是处理进位了,我们知道^是进行无进位相加,那如果我们想得到进位的数字呢?
简单,直接(a&b)<<1就可以得到进位(进位要往前面移动)了,我们来举例子看看:

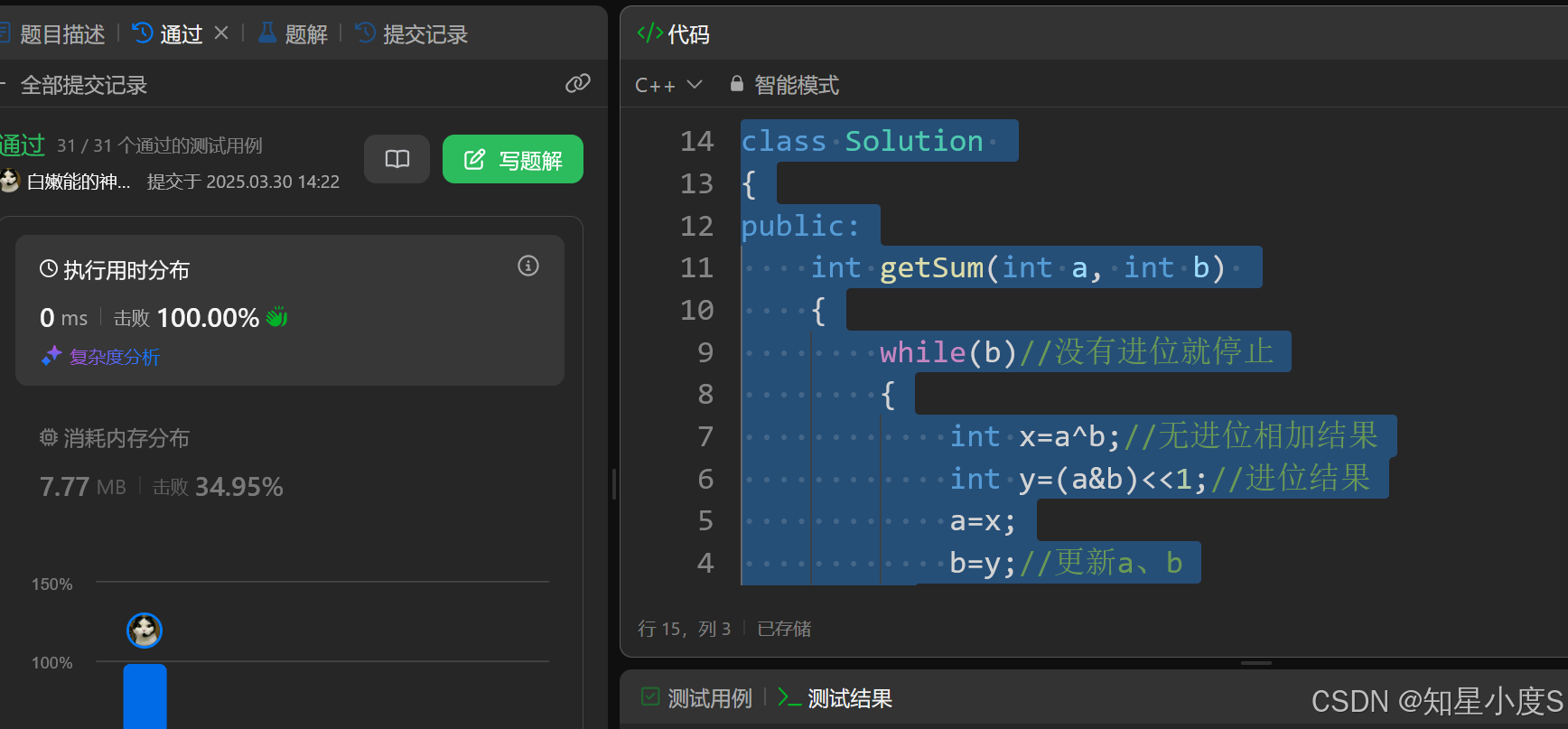
思路:不断地进行a^b得到无进位相加的结果,(a&b)<<1得到进位的结果,直到没有进位就得到想要的结果~
代码:
class Solution
{
public:
int getSum(int a, int b)
{
while(b)//没有进位就停止
{
int x=a^b;//无进位相加结果
int y=(a&b)<<1;//进位结果
a=x;
b=y;//更新a、b
}
return a;
}
};
顺利通过~
只出现一次的数字Ⅱ
这个题目有点难度了,有一个数字出现了一次,其他数字出现了三次~
宏观上,我们不太好分析,我们来看看微观上,来看看一个整型的比特位,既然其他数字出现了三次,那么每一个比特位的结果可能是:
3n个0+1 3n个1+1 3n个0+0 3n个1+0 如果%3的结果不就是我们想要的出现一次的数字该比特位是0还是1吗?
思路:统计整型数组元素每一个比特位的和,和%3得到出现一次的数字该比特位,是1就进行修改~
代码:
class Solution
{
public:
int singleNumber(vector<int>& nums)
{
int ret=0;
//统计每一个比特位的和
for(int i=0;i<32;i++)
{
int sum=0;
for(auto e:nums)
{
if(((e>>i)&1)==1)
sum++;//统计所有数据该比特位为1的个数
}
sum%=3;
if(sum==1) //多的就是出现一次数字的
ret|=(1<<i);//修改ret的该比特位为1
}
return ret;
}
};
事实上,这个题目不仅仅可以处理其他数据出现3次,还可以处理其他数据出现k次~方法都是一样的~
比如前面其他数据出现两次,只需要修改为sum%=2就可以了~
class Solution
{
public:
int singleNumber(vector<int>& nums)
{
int ret=0;
//统计每一个比特位的和
for(int i=0;i<32;i++)
{
int sum=0;
for(auto e:nums)
{
if(((e>>i)&1)==1)
sum++;//统计所有数据该比特位为1的个数
}
sum%=2;
if(sum==1) //多的就是出现一次数字的
ret|=(1<<i);//修改ret的该比特位为1
}
return ret;
}
};
只出现一次的数据Ⅲ
这个题目有点难度,我们废话不多说,直接来思路:
思路: A、将所有的数据进行异或,异或得到的结果就是那两个只出现一次的数据异或的结果 B、根据异或的结果找到某一个为1的比特位(根据异或的相同为0,相异为1),比特位为1,说明这两个数据这个比特位是不同的 C、根据找到的比特位把数据分为两组,一组该比特位为1进行异或,一组该比特位为0进行异或,因为其他因素出现了两次,两组得到的结果就是我们想要的结果
代码:
class Solution
{
public:
vector<int> singleNumber(vector<int>& nums)
{
//1、异或所有的数
int tmp=0;
for(auto e:nums) tmp^=e;
//tmp就是两个出现一次数异或的结果
//2、找到为1的比特位
int dicone=0;
while(1)
{
if(((tmp>>dicone)&1)==1) break;
else dicone++;
}
//3、根据dicone进行分组
//既然dicone不同,两个不同的数字一定不会出现在一组
int x=0,y=0;
for(auto e:nums)
{
if(((e>>dicone)&1)==1) x^=e;
else y^=e;
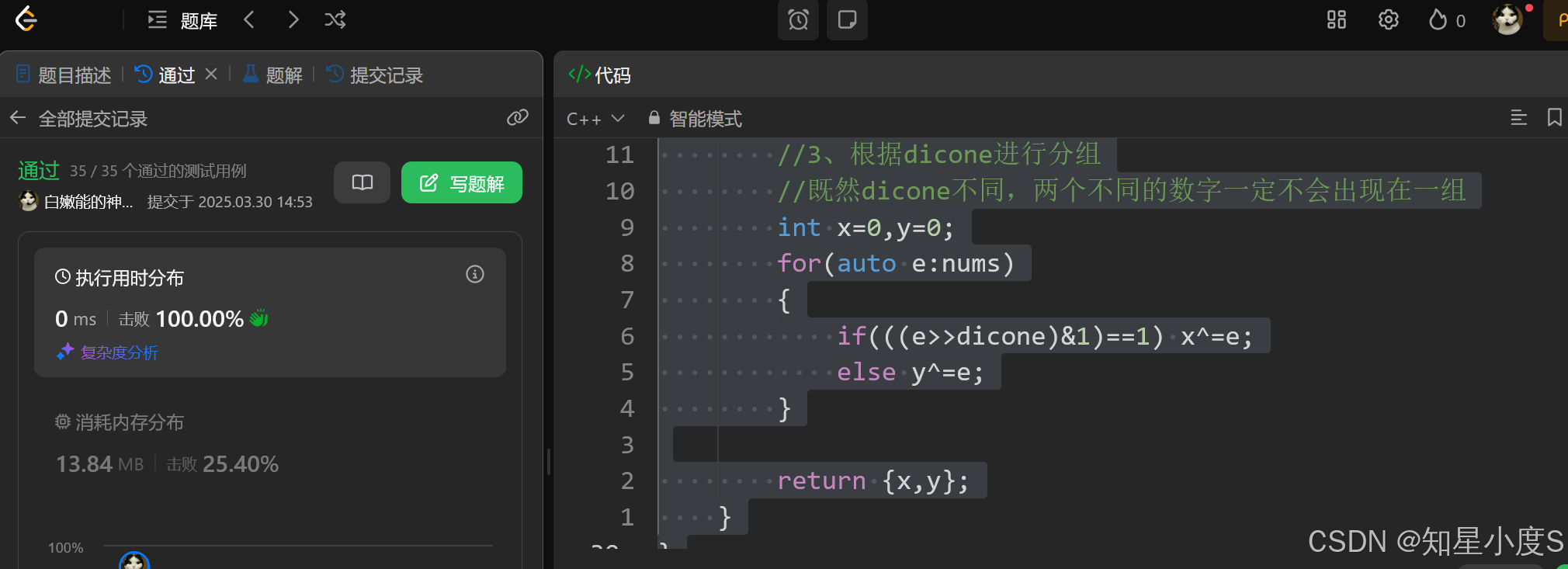
}
return {x,y};
}
};
顺利通过~
消失的两个数字
有了前面的基础,相信这一道题目就比较简单了,事实上,与只出现一次的数字Ⅲ方法是类似的,如果我们再有1~N的数据,那么不就是两个数字出现一次,其他数据出现两次了吗~
思路: A0:加上1~N的数据 A、将所有的数据进行异或,异或得到的结果就是那两个只出现一次的数据异或的结果 B、根据异或的结果找到某一个为1的比特位(根据异或的相同为0,相异为1),比特位为1,说明这两个数据这个比特位是不同的 C、根据找到的比特位把数据分为两组,一组该比特位为1进行异或,一组该比特位为0进行异或,因为其他因素出现了两次,两组得到的结果就是我们想要的结果
代码:
class Solution
{
public:
vector<int> missingTwo(vector<int>& nums)
{
//1、所有的数据进行异或
int ret=0;
for(auto e:nums)
{
ret^=e;
}
//获取1~n的数据
for(int n=1;n<=nums.size()+2;n++)
{
ret^=n;
}
//2、找到比特位为一的那一位
int dicone=0;
while(1)
{
if(((ret>>dicone)&1)==1) break;
else dicone++;
}
//3、根据比特位分组异或
int x=0,y=0;
for(auto e:nums)
{
if(((e>>dicone)&1)==1) x^=e;
else y^=e;
}
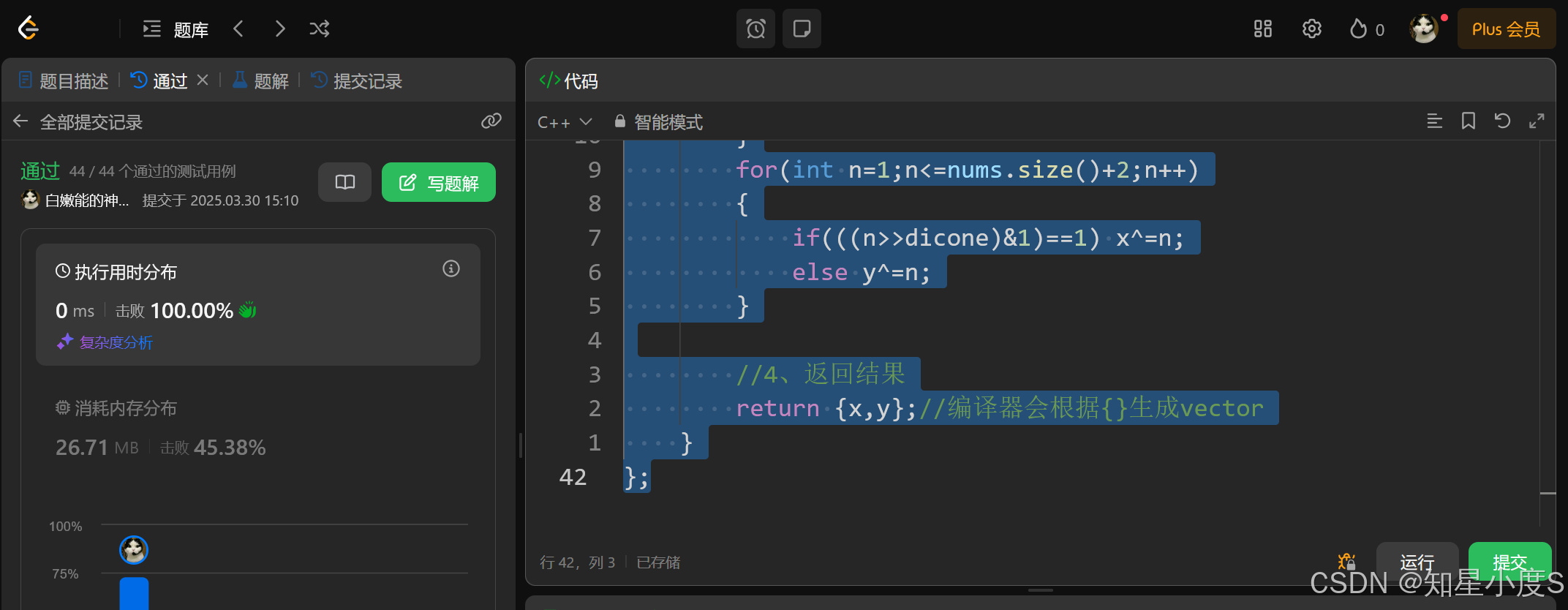
for(int n=1;n<=nums.size()+2;n++)
{
if(((n>>dicone)&1)==1) x^=n;
else y^=n;
}
//4、返回结果
return {x,y};//编译器会根据{}生成vector
}
};
顺利通过~
位运算具有高效性、简洁性、灵活性和性能优化等优势。它直接操作二进制位,执行速度快且资源消耗低,代码简洁易读,提供多种操作方式,适用于算法优化和底层硬件操作,是我们在编程中不可或缺的重要工具~所以合理正确的使用会给我们带来很大的方便~
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-04-09,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

