遗传算法：自然选择的计算艺术

熊猫钓鱼

发布于 2025-08-01 16:53:39

2240

在优化问题的迷雾森林中，遗传算法犹如达尔文主义的灯塔，将生物进化原理转化为强大的计算范式。当传统优化方法在复杂地形中步履维艰时，这种模拟自然选择的智能算法展现出惊人的适应能力——它不依赖目标函数的梯度信息，不畏惧多峰搜索空间的局部陷阱，而是通过种群进化的集体智慧探索解空间。遗传算法的核心思想在于将问题解编码为染色体，在选择压力下通过遗传操作实现解的迭代优化，最终逼近全局最优解。这种计算框架的优雅之处在于其通用性：从航天器轨道设计到神经网络架构搜索，从蛋白质折叠预测到金融投资组合优化，遗传算法以统一的生物学隐喻解决千差万别的工程问题。

自然选择的计算映射

遗传算法的理论基础建立在三大进化机制之上：

遗传编码：将解空间映射为基因型空间
- 二进制编码：解向量 → 01字符串（如110010代表数字50）
- 实数编码：直接使用浮点数向量（如[3.14, 2.71]）
- 排列编码：用于顺序问题（如旅行商路径[A,C,B,D]）
适应度函数：自然选择的数学表述
进化算子：
- 选择：轮盘赌
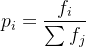$\quad p_i = \frac{f_i}{\sum f_j}$
$\quad p_i = \frac{f_i}{\sum f_j}$
- 交叉：单点/多点/均匀交叉
- 变异：位翻转/高斯扰动/互换变异

实现代码如下：

# 基本遗传算法框架
def genetic_algorithm(pop_size, generations, crossover_rate, mutation_rate):
    population = initialize_population(pop_size)  # 种群初始化
    
    for gen in range(generations):
        fitness = evaluate(population)            # 适应度评估
        new_population = []
        
        while len(new_population) < pop_size:
            parent1 = select(fitness, population) # 选择
            parent2 = select(fitness, population)
            
            if random.random() < crossover_rate:   # 交叉
                child1, child2 = crossover(parent1, parent2)
            else:
                child1, child2 = parent1, parent2
                
            child1 = mutate(child1, mutation_rate) # 变异
            child2 = mutate(child2, mutation_rate)
            
            new_population.extend([child1, child2])
        
        population = new_population
    
    return best_solution(population)

遗传算子深度剖析

选择机制：适者生存的计算实现

轮盘赌选择虽直观但存在选择偏差，现代算法采用更精确的机制：

# 随机遍历抽样（Stochastic Universal Sampling）
def sus_selection(fitness, population, n):
    total_fitness = sum(fitness)
    step = total_fitness / n
    start = random.uniform(0, step)
    pointers = [start + i*step for i in range(n)]
    
    selected = []
    cum_fitness = 0
    idx = 0
    for ptr in pointers:
        while cum_fitness < ptr:
            cum_fitness += fitness[idx]
            idx = (idx + 1) % len(population)
        selected.append(population[idx-1])
    
    return selected

锦标赛选择避免全局适应度计算：

def tournament_selection(population, fitness, k=3):
    tournament = random.sample(list(zip(population, fitness)), k)
    winner = max(tournament, key=lambda x: x[1])[0]
    return winner

交叉操作：基因重组艺术

模拟二进制交叉（SBX） 保持种群多样性：

def sbx_crossover(parent1, parent2, eta_c=20):
    child1, child2 = [], []
    for i in range(len(parent1)):
        u = random.random()
        if u <= 0.5:
            gamma = (2*u)**(1/(eta_c+1))
        else:
            gamma = (1/(2*(1-u)))**(1/(eta_c+1))
        
        c1 = 0.5*((1+gamma)*parent1[i] + (1-gamma)*parent2[i])
        c2 = 0.5*((1-gamma)*parent1[i] + (1+gamma)*parent2[i])
        
        child1.append(c1)
        child2.append(c2)
    
    return np.array(child1), np.array(child2)

变异策略：创新的源泉

自适应变异动态调整强度：

def adaptive_mutation(individual, gen, max_gen, mutation_rate):
    mutated = individual.copy()
    for i in range(len(mutated)):
        if random.random() < mutation_rate:
            # 随着代数增加减小变异幅度
            delta = (1 - gen/max_gen)**2 * random.gauss(0, 1)
            mutated[i] += delta
            # 边界处理
            mutated[i] = max(min(mutated[i], upper_bound), lower_bound)
    return mutated

进化计算的高级范式

多目标优化：帕累托前沿探索

NSGA-II算法实现：

def nsga2(population, fitness_values):
    # 快速非支配排序
    fronts = fast_non_dominated_sort(fitness_values)
    
    # 拥挤度计算
    crowding_distances = []
    for front in fronts:
        crowding = crowding_distance(fitness_values[front])
        crowding_distances.append(crowding)
    
    # 精英保留
    new_pop = []
    for i, front in enumerate(fronts):
        if len(new_pop) + len(front) <= POP_SIZE:
            new_pop.extend(front)
        else:
            sorted_front = [x for _, x in sorted(zip(crowding_distances[i], front), reverse=True]
            new_pop += sorted_front[:POP_SIZE-len(new_pop)]
            break
    
    return new_pop

并行进化：岛屿模型

from mpi4py import MPI

comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()

# 每个岛屿独立进化
island_pop = initialize_population(POP_SIZE//size)
for gen in range(GENERATIONS):
    island_pop = evolve(island_pop)
    
    # 定期迁移
    if gen % MIGRATION_INTERVAL == 0:
        # 选择迁移个体
        migrants = select_migrants(island_pop)
        # 环状迁移拓扑
        comm.send(migrants, dest=(rank+1)%size)
        received = comm.recv(source=(rank-1)%size)
        # 替换最差个体
        island_pop = integrate_migrants(island_pop, received)

工程实践：函数优化案例

求解Rastrigin函数最小值：

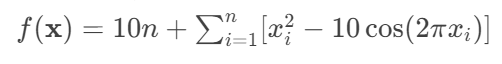
import numpy as np

def rastrigin(x):
    """Rastrigin函数 (多峰测试函数)"""
    n = len(x)
    return 10*n + sum(xi**2 - 10*np.cos(2*np.pi*xi) for xi in x)

# 遗传算法实现
class GeneticOptimizer:
    def __init__(self, dim, pop_size=100, 
                 crossover_rate=0.9, mutation_rate=0.1,
                 elitism=True):
        self.dim = dim
        self.pop_size = pop_size
        self.crossover_rate = crossover_rate
        self.mutation_rate = mutation_rate
        self.elitism = elitism
        self.bounds = [-5.12, 5.12]  # Rastrigin函数定义域
        
    def initialize(self):
        return np.random.uniform(*self.bounds, size=(self.pop_size, self.dim))
        
    def evaluate(self, pop):
        return np.array([-rastrigin(ind) for ind in pop])  # 负号转为最大化问题
    
    def select(self, fitness):
        probs = fitness / fitness.sum()
        return np.random.choice(len(pop), size=2, p=probs, replace=False)
    
    def crossover(self, parent1, parent2):
        if np.random.rand() < self.crossover_rate:
            # 模拟二进制交叉
            return sbx_crossover(parent1, parent2)
        return parent1.copy(), parent2.copy()
    
    def mutate(self, individual):
        for i in range(self.dim):
            if np.random.rand() < self.mutation_rate:
                # 多项式变异
                u = np.random.rand()
                if u < 0.5:
                    delta = (2*u)**(1/20) - 1
                else:
                    delta = 1 - (2*(1-u))**(1/20)
                individual[i] += delta * (self.bounds[1]-self.bounds[0])
                # 边界检查
                individual[i] = np.clip(individual[i], *self.bounds)
        return individual
    
    def evolve(self, generations=100):
        pop = self.initialize()
        best_fitness = []
        
        for gen in range(generations):
            fitness = self.evaluate(pop)
            best_idx = np.argmax(fitness)
            best_fitness.append(-fitness[best_idx])  # 记录实际函数值
            
            new_pop = []
            if self.elitism:
                new_pop.append(pop[best_idx])  # 精英保留
            
            while len(new_pop) < self.pop_size:
                idx1, idx2 = self.select(fitness)
                p1, p2 = pop[idx1], pop[idx2]
                
                c1, c2 = self.crossover(p1, p2)
                c1 = self.mutate(c1)
                c2 = self.mutate(c2)
                
                new_pop.extend([c1, c2])
            
            pop = np.array(new_pop)[:self.pop_size]
            
            # 输出进度
            if gen % 10 == 0:
                print(f"Gen {gen}: Best = {best_fitness[-1]:.4f}")
        
        return pop, best_fitness

# 运行优化
optimizer = GeneticOptimizer(dim=10)
population, history = optimizer.evolve(generations=200)