(JAVA)加权无向图和最小生成树的实现与原理概述
(JAVA)加权无向图和最小生成树的实现与原理概述
1. 加权无向图
1.1 加权无向图的概述
加权无向图是一种为每条边关联一个权重值或是成本的图模型。这种图能够自然地表示许多应用。在一副航空图中,边表示航线,权值可以表示距离或是费用。在一副电路图中,边表示导线,权值表示导线的长度即成本,或是信号通过这条线所需的时间。此时我们很容易就能想到,最小成本的问题,例如,从西安飞纽约,怎样飞才能使时间成本最低或者使金钱成本最低?
在下图中,从顶点0到顶点4有三条路径,分别使0-2-3-4,0-2-4,0-5-3-4,哪我们如果要通过哪条路径到达4顶点最好呢?此时就要考虑,哪条路径的成本最低。
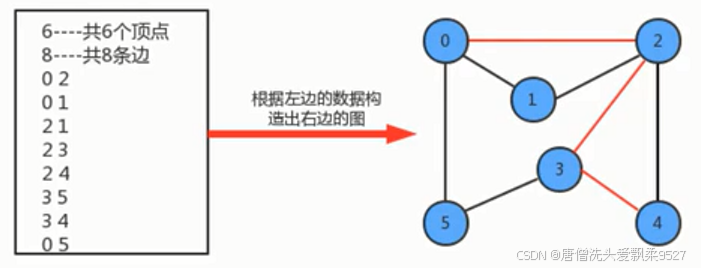
1.2 加权无向图的表示
加权无向图中的边我们就不能简单的使用 v-2 两个顶点来表示了,而必须要给边关联一个权重值,因此我们可以使用对象来描述一条边。
1.2.1 API 设计:
类名 | Edge implements Comparable<Edge> |
|---|---|
构造方法 | Edge(int v,int w,double weight):通过顶点v和w,以及权重weight值构造一个边对象 |
成员方法 | 1. public double weight():获取边的权重值2. public int either():获取边上的一个点3. public int other(int vertex):获取边上除了顶点vertex外的另一个顶点4. public int compareTo(Edge that):比较当前边和参数that边的权重,如果当前边权重大,返回1,如果一样大,返回0,如果当前权重小,返回-1 |
成员变量 | 1. private final int v:顶点一2. private final int w:顶点二3. private final double weight:当前边的权重 |
1.3 加权无向图的实现
1.3.1 API 设计
类名 | EdgeWeightGraph |
|---|---|
构造方法 | EdgeWeightedGraph(int v):创建一个含有v个顶点的空加权无向图 |
成员方法 | 1. public int V():获取图中顶点的数量2. public int E():获取图中边的数量3. public void addEdge(Edge e):向加权无向图中添加一条边4. public Queue<Edge> adj(int v):获取和顶点v关联的所有边5. public Queue<Edge> edges():获取加权无向图的所有边 |
成员变量 | 1. private final int V:记录顶点数量2. private int E:记录边数量3. private Queue<Edge>[] adj:邻接表 |
2. 最小生成树
之前学习的加权图,我们发现它的边关联的一个权重,那么我们就可以根据这个权重解决最小成本问题,但如何才能找对最小成本对应的顶点和边呢?最小生成树 可以解决
2.1 最小生成树定义及相关约定
2.1.1 定义:
图的生成树是它的一颗含有其所有顶点的无环连通子图,一副加权无向图的最小生成树就是它的一颗权值(树中所有边的权重之和)最小的生成树
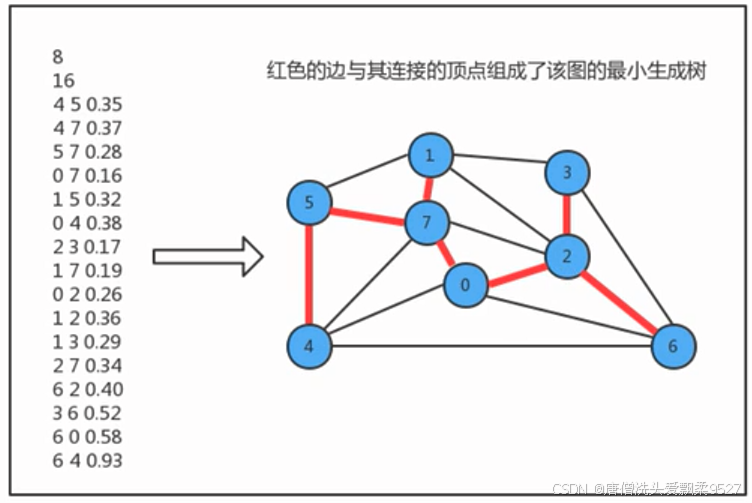
2.1.2 约定:
最小生成树 只考虑连通图,最小生成树的定义说明它只能存在于连通图中,如果图不是连通的,那么分别计算每个连通子图的最小生成树,合并到一起称为最小生成森林
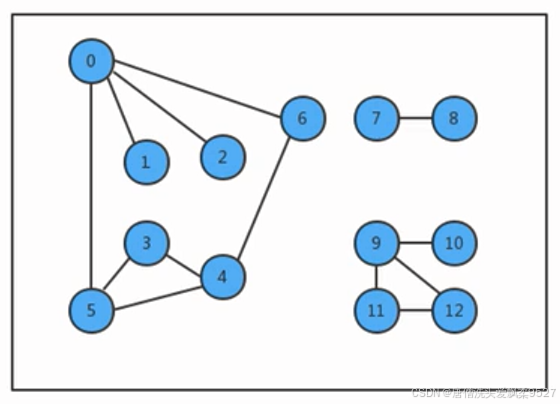
所有边的权重都各不相同,如果不同的边权重可以相通,那么一副图的最小生成树就可能不唯一了,虽然我们的算法可以处理这种情况,但为了好理解,我们约定所有边的权重都各不相同
2.2 最小生成树原理
2.2.1 树的性质
- 用一条边连接树中的任意两个顶点都会产生一个新的环;
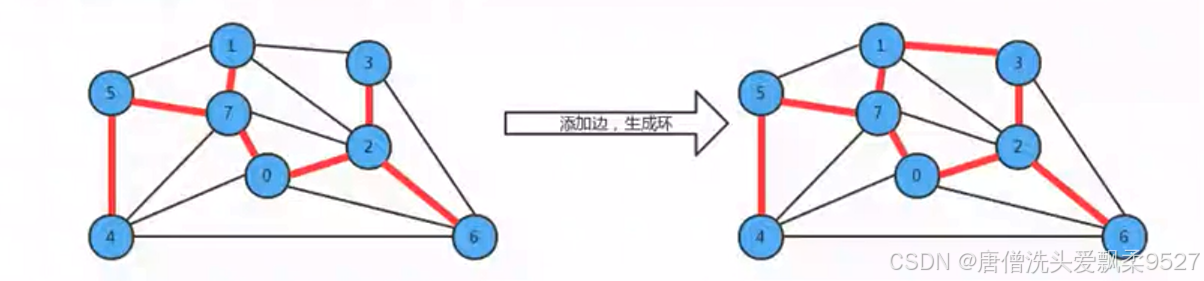
- 从树中删除任意一条边,将会得到两颗独立的树;
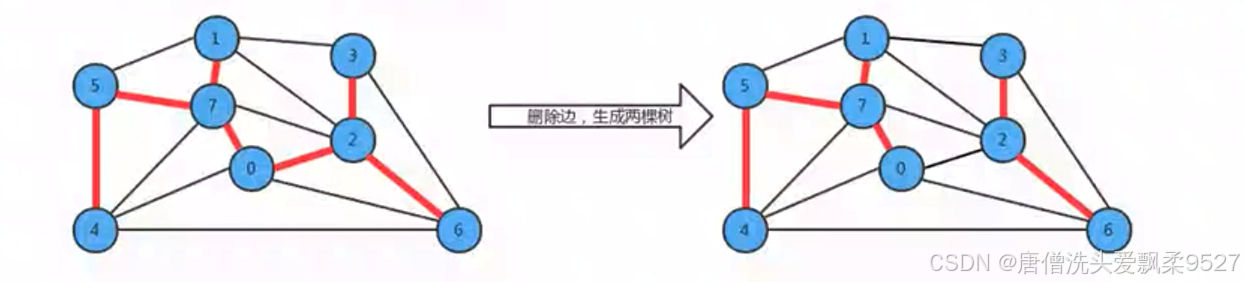
2.2.2 切分定理
要从一副连通图中找出该图的最小生成树,需要通过切分定理完成。
切分:
- 将图的所有顶点按照某些规则分为两个非空且没有交集的集合。
横切边:
- 连接两个属于不同集合的顶点的边称之为横切边
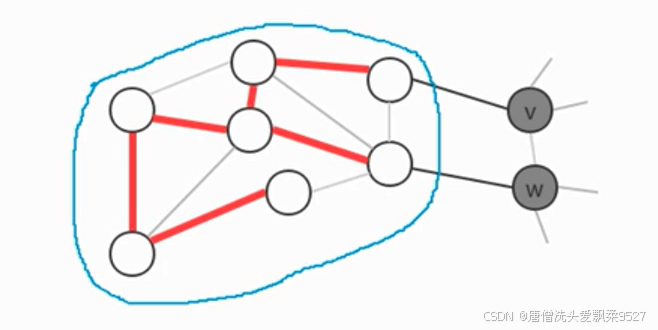
- 例如我们将图中的顶点切分为两个集合,灰色顶点属于一个集合,白色顶点属于另外一个集合,那么效果如下:
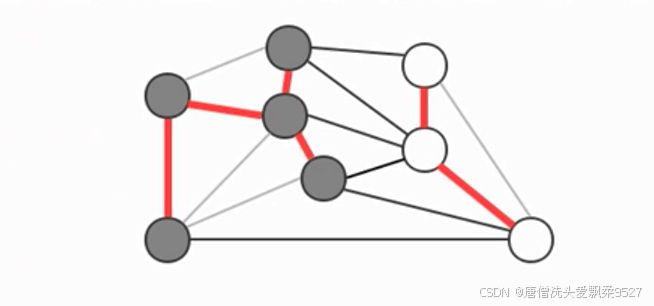
切分定理:
- 在一副加权图中,给定任意的切分,它的横切边中的权重最小者必然属于图中的最小生成树
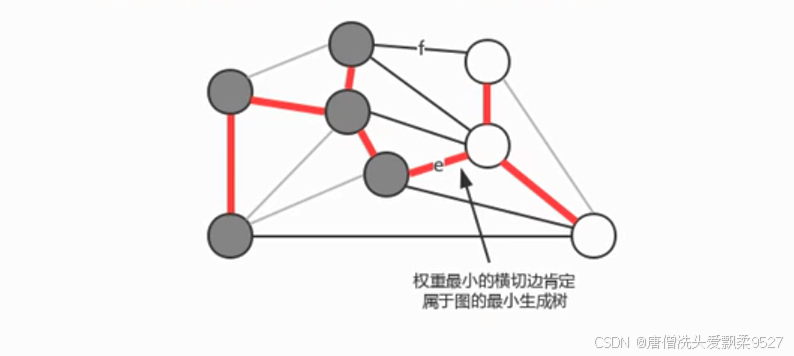
- **注意:**一次切分产生多个横切边中,权重最小的边不一定是所有横切边中唯一属于图的最小生成树的边
2.2.3 贪心算法
贪心算法是计算图的最小生成树的基础算法,它的基本原理就是切分定理,使用切分定理找到最小生成树的一条边,不断的重复直到找到最小生成树的所有边。
如果图有V个顶点,那么需要找 V-1 条边,就可以表示该图的最小生成树
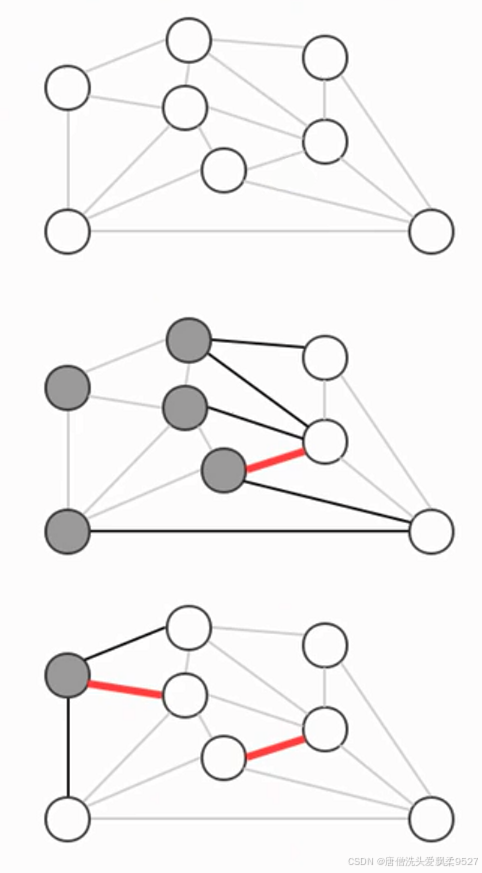
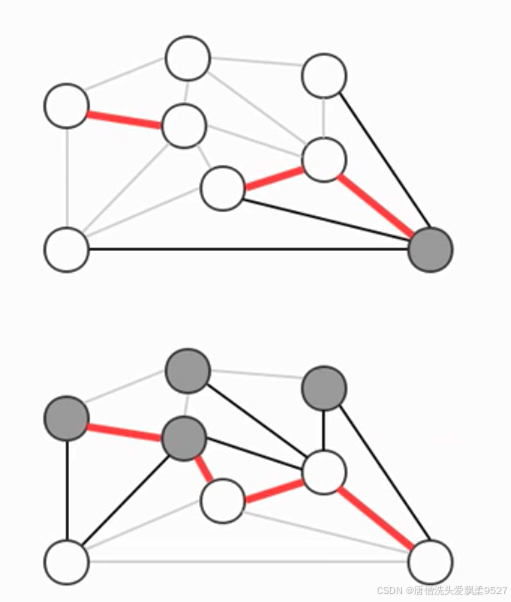
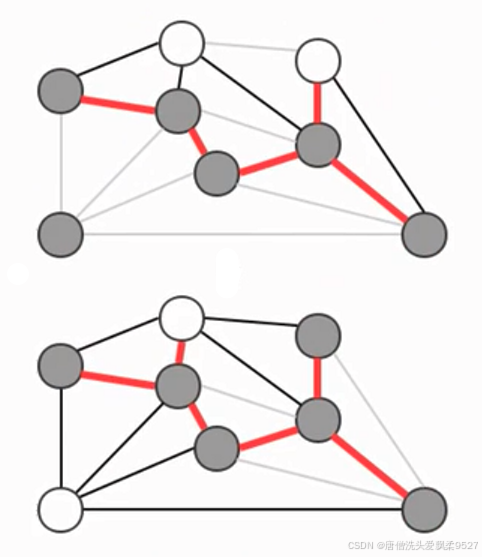
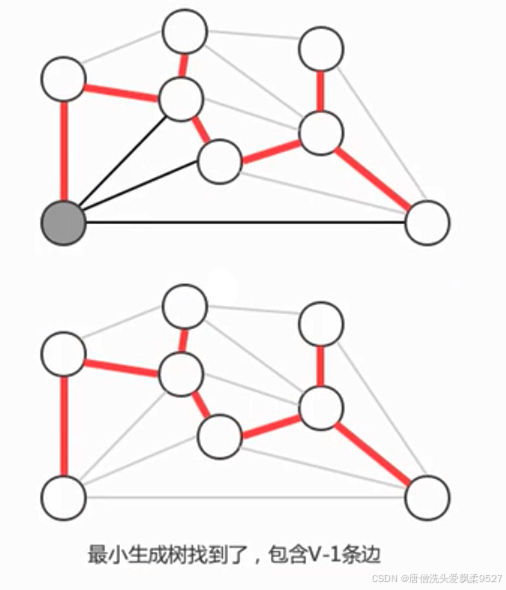
计算图的最小生成树的算法有很多种,但这些算法都可以看作是贪心算法的一种特殊情况,这些算法的不同指出在于保存切分和判定权重最小的横切边方式
更多关于 贪心算法 的知识 可以在我的新一篇文章中查询到喔~!!
2.2.4 Prim 算法
V :某顶点的邻接表中所有的顶点
计算最小生成树的算法:Prim算法,它的每一步都会为一棵生成的树添加一条边。一开始这棵树只有一个顶点,然后会向它添加 V-1条边,每次总是将下一条连接树中的顶点与不再树种的顶点且权重最小的边加入到树中。
2.2.4.1 Pirm算法切分规则:
把最小生成树中的顶点看作是一个集合,把不再最小生成树中的顶点看作是另外一个集合。
2.2.4.2 Prim算法API设计
类名 | PrimMST |
|---|---|
构造方法 | PrimMST(EdgeWeightedGraph G):根据一副加权无向图,创建最小生成树计算对象 |
成员方法 | 1. private void visit(EdgeWeightedGraph G,int V):将顶点v添加到最小生成树中,并且更新数据2. public Queue<Edge> edges():获取最小生成树的所有边 |
成员变量 | 1. private Edge[] edgeTo:索引代表顶点,值表示当前顶点和最小生成树之间的最短边2. private double[] distTo:索引代表顶点,值表示当前顶点和最小生成树之间的最短边的权重3. private boolean[] marked:索引代表顶点,如果当前顶点已经在树中,则值为true,否则为false4. private indexMinPriorityQueue<Double> pq:存放树中和非树中顶点之间的有效横切边 |
2.2.4.3 Prim算法的实现原理
Prim算法始终将图中的顶点切分成两个集合,最小生成树和非最小生成树顶点,通过不断的重复做某些操作,可以主键将非最小生成树中的顶点加入到最小生成树中,直到所有的顶点,都加入到最小生成树中
在设计API的时候,使用最小索引优先队列存放树中顶点与非树中顶点的有效横切边,那么它是如何表示的呢?我们可以让最小索引处优先队列的索引值表示圆的顶点,让最小索引优先队列中的值表示其他某个顶点到当前顶点的边权重。
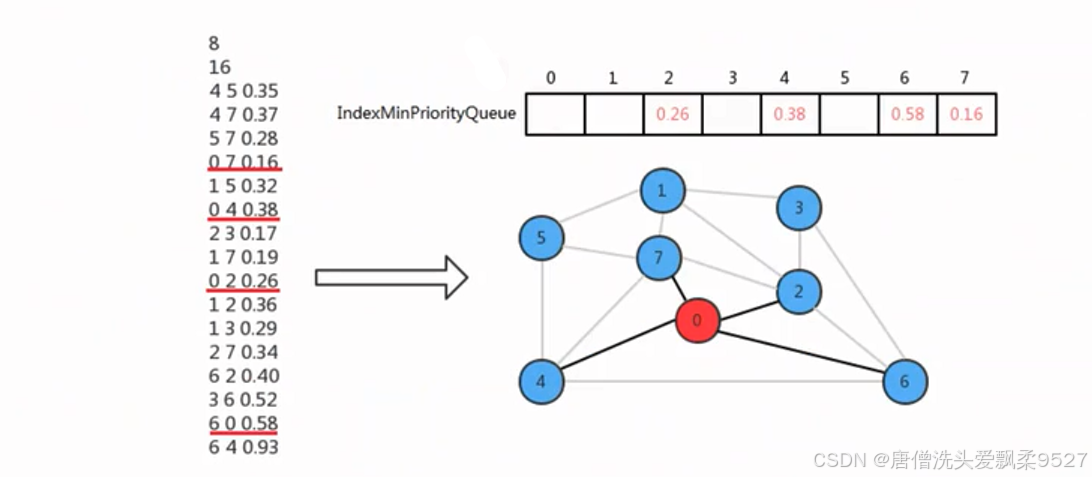
初始化状态,线默认0是最小生成树中的唯一顶点,其他的顶点都不再最小生成树中,此时横切边就是顶点0的邻接表中0-2,0-4,0-6,0-7这四条边,我们只需要将索引优先队列的2、4、6、7索引处分别存储这些边的权重值就可以表示了
现在只需要从这四条横切边中找出权重最小的边,如何把对应的顶点加进 最小生成树 中即可。
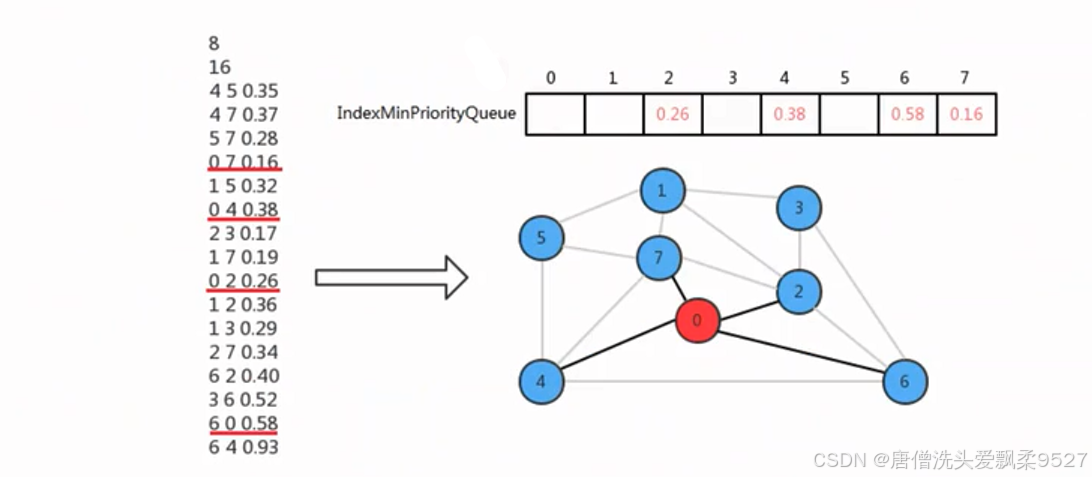
所以找到0-7这条横切边的权重最小,因此0-7这条边添加进来,此时0和7属于最小生成树的顶点。其他的不属于,现在顶点7的邻接表中的边也成为了横切边,这时需要做两个操作:
- 0-7这边已经不是横切边了,需要让它失效: 只需要调用最小索引优先队列的delMin()方法即可完成;
- 2和4顶点各有两条连接指向最小生成树,需要只保留一条: 4-7的权重小于0-4的权重,所以保留4-7,调用所以优先队列的change(4,0.37)即可 0-2的权重小于2-7的权重,所以保留0-2,不需要做额外操作
2.2.4.4 Prim算法实现
package com.renecdemo.prim;
import com.renecdemo.graph.Queue;
import com.renecdemo.queue.IndexMinPriorityQueue;
import com.renecdemo.weighted.Edge;
import com.renecdemo.weighted.EdgeWeightedGraph;
// Prim算法实现最小生成树
public class PrimMST {
// 索引代表顶点,值表示当前顶点和最小生成树之间的最短边
private Edge[] edgeTo;
// 索引代表顶点,值表示当前顶点和最小生成树之间的最短边的权重
private double[] distTo;
// 索引代表顶点,如果当前顶点已经在树中,则值为true,否则为false
private boolean[] marked;
// 存放树中和非树中顶点之间的有效横切边
private IndexMinPriorityQueue<Double> pq;
// 根据一副加权无向图,创建最小生成树计算对象
public PrimMST(EdgeWeightedGraph G) {
// 初始化变量
this.edgeTo = new Edge[G.V()];
this.distTo = new double[G.V()];
// 初始化权重
for (int i = 0; i < distTo.length; i++) {
// 让double数组中的每个值都等于Double类型所能存储的最大值
// 当权重默认为无限大时,意味着该边永远不可能是最短边
distTo[i] = Double.POSITIVE_INFINITY;
}
this.marked = new boolean[G.V()];
this.pq = new IndexMinPriorityQueue<Double>(G.V());//16
// 默认让顶点0进入到树中,当树中只有一个顶点0
distTo[0] = 0.0;// 顶点0 的权重为 0.0
pq.insert(0,0.0);// 它的横切边为 0, 该边权重为0.0
// 遍历所以最小优先队列
while (!pq.isEmpty()){
// 切分 - 对 顶点0 进行切分
visit(G,pq.delMin());
}
}
// 将顶点v添加到最小生成树中,并且更新数据
private void visit(EdgeWeightedGraph G,int v){
// 把顶点v添加到最小生成树中
marked[v] = true;// 标识 顶点v 在树中已存在
/*
遍历 G图 中 顶点v 的邻接表
*/
for (Edge e : G.adj(v)) {
int w = e.other(v);// 获得v顶点外的另一个顶点
/*
判断 w 顶点是否在树中,如果在,那么进行下一次循环
- 如果 w顶点 在树中就无需为w顶点添加到树中了
*/
if (marked[w]){
continue;
}
/*
判断边 e边 的权重是否小于从w到树中已经存在最小边的权重
- 小于才做更新操作
*/
if (e.weight()<distTo[w]){
// 更新数据;更新记录的权重和最短边
edgeTo[w] = e;
distTo[w] = e.weight();
// 更改优先队列中顶点的权重
if (pq.contains(w)){
pq.changeItem(w,e.weight());
}else {
pq.insert(w,e.weight());
}
}
}
}
// 获取最小生成树的所有边
public Queue<Edge> edges(){
// 创建队列edges
Queue<Edge> allEdge = new Queue<>();
for (int i = 0; i < edgeTo.length; i++) {
if (edgeTo[i] != null){
allEdge.enqueue(edgeTo[i]);
}
}
return allEdge;
}
}2.2.5 Kruskal 算法
Kruskal算法师计算一副加权无向图的最小生成树的另外一种算法,它的主要思想是按照边的权重(从小到大)处理它们,及那个边加入最小生成树中,加入的边不会与已经加入最小生成树的边构成环,直到树中含有V-1条边为止
2.2.5.1 Kruskal算法和Prim算法的区别:
Pirm算法 是一条边一条边的构造最小生成树,每一步都为一棵树添加一条边。
kruskal算法 构造最小生成树的时候也是一条边一条边的构造,但它的切分规则不一样。
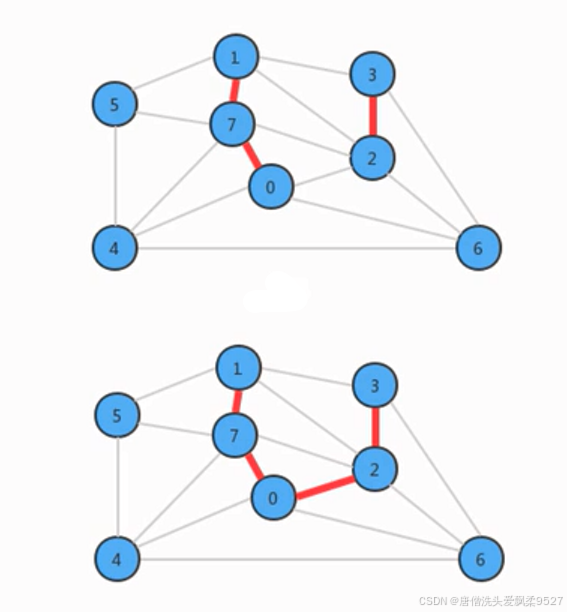
- 它每次寻找的边会连接一篇森林中的两棵树。
- 如果一副加权无向图由V个顶点组成,初始化情况下每个顶点都构成一颗独立的树,则V个顶点对应V棵树,组成一片森林,
- kruskal算法每一次处理都会将两棵树合并为一棵树,直到整个森林中只剩一棵树为止。
2.2.5.2 API 设计
类名 | KruskalMST |
|---|---|
构造方法 | KruskalMST(EdgeWeightedGraph G):根据一副加权无向图,创建最小生成树计算对象 |
成员方法 | 1. public Queue<Edge> edges():获取最小生成树的所有边 |
成员变量 | 1. private Queue<Edge> mst:保存最小生成树的所有边2. private UF_Tree_Weighted uf:索引代表顶点,使用connect方法可以判断两个顶点是否在同一颗树种,使用union方法可以将两个顶点所在的树合并3. private MinPriorityQueue<Edge> pq:存储图中所有的边,使用最小优先队列,对边按照权重进行排序 |
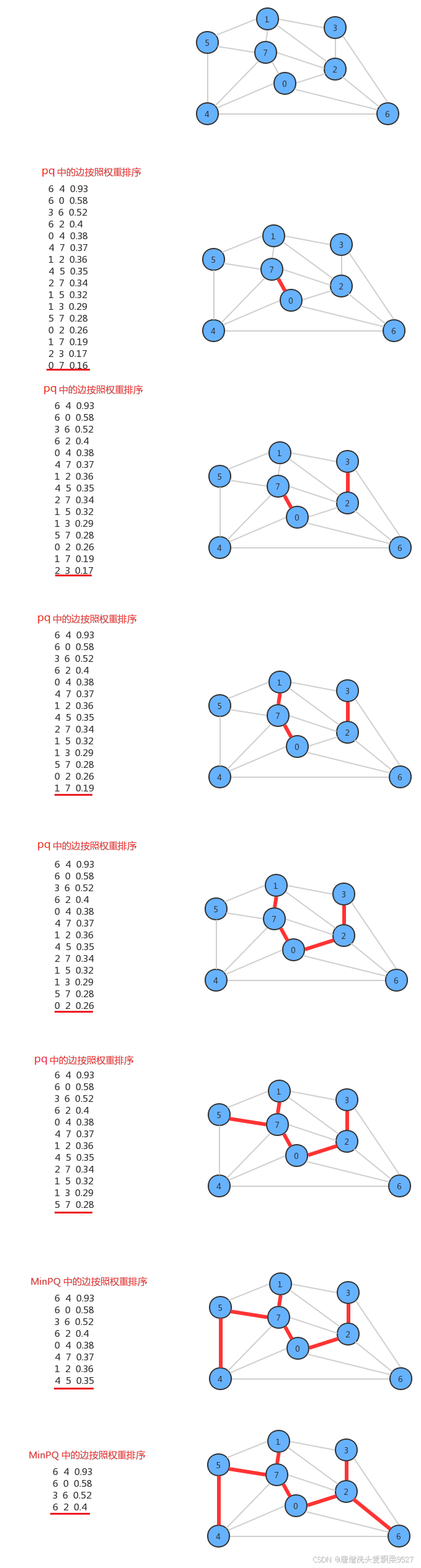
2.2.5.3 kruskal 算法的原理
在设计API的时候,使用了MinpriorityQueue<Edge> pq存储图中所有的边,每次使用pq.delMin()取出权重最小的边,并得到该边关联的两个顶点v和w,通过uf.connect(v,w)判断v和w是否已经连通。
- 如果连通则证明这两个顶点在同一棵树中,那么就不能再把这条边添加到最小生成树中,因为在一棵树的任意两个顶点上添加一条边,都会形成环,而最小生成树不能有环的存在。
- 如果不连通,则通过uf.connect(v,w)把顶点v所在的树和顶点w所在的树合并成一棵树,并把这条边加入到mst队列中,这样如果把所有的边处理完,最终mst中存储的就是最小生成树的所有边
2.2.5.4 kruskal 算法实现
package com.renecdemo.graph;
import com.renecdemo.queue.MinPriorityQueue;
import com.renecdemo.weighted.Edge;
import com.renecdemo.weighted.EdgeWeightedGraph;
import com.renexdemo.tree.UF_Tree_Weighted;
/**
* Kruskal 算法实现
*/
public class KruskalMST {
// 保存最小生成树的所有边
private Queue<Edge> mst;
/**
* 索引代表顶点,
* 使用connect方法可以判断两个顶点是否在同一颗树中,
* 使用union方法可以将两个顶点所在的树合并
*/
private UF_Tree_Weighted uf;
// 存储图中所有的边,使用最小优先队列,对边按照权重进行排序
private MinPriorityQueue<Edge> pq;
/**
* 初始化构造
* @param G
*/
public KruskalMST(EdgeWeightedGraph G){
// 初始化
this.mst = new Queue<>();
this.uf = new UF_Tree_Weighted(G.V());
this.pq = new MinPriorityQueue<>(G.E()+1);
// 把图中所有的边添加到pq中
for (Edge e : G.edges()) {
pq.insert(e);
}
/*
pq数组不为空
并且
最小生成树的所有边不应该小于子图中顶点数-1
- 如果所有边小于 子图中顶点数-1 那么代表最小生成树已经规划完毕
*/
while (!pq.isEmpty() && mst.size() < G.V()-1){
// 找到权重最小的边
Edge e = pq.delMin();
// 找到该边的两个顶点
int v = e.either();
int w = e.other(v);
// 判断这两个顶点是否已经在同一棵树中
if (uf.connected(v,w)){
// 在一棵数中不做处理直接跳过当前循环
continue;
}
// 不再一棵树中,那么合并
uf.union(v,w);
// 让边e进入到mst队列汇总
mst.enqueue(e);
}
}
/**
* 获取最小生成树的所有边
* @return
*/
public Queue<Edge> edges(){
return mst;
}
}2.2.6 Prim 算法和 Kruskal 算法的实现对比
- Prim 算法: prim算法 默认将顶点0作为最小生成树,通过不断找该顶点邻接表中的最短权重边,找到边后添加进记录数组中,当顶点0边找寻完毕,那么找到这条最短权重边的另一个顶点(顶点1),对 顶点1 进行再次查找该顶点的邻接表中的最短权重边,当找寻完毕再次找该顶点的另一个顶点,以此循环。最后返回记录数组,那么最小生成树就是该数组
- Kruskal算法: Kruskal算法 默认将图中所有的顶点都看作是最小生成树,形成森林状,并将所有边都按照权重排序添加进最小索引优先队列中,按照队列中的权重对树进行循环合并,循环合并到最后,最后合并的树就成为了最小生成树
- 个人理解: 从代码量上来说,Kruskal算法比Prim算法要少,但是从逻辑上来说,Prim算法比Kruskal算法要简单。 而从时间复杂度上来说,Kruskal算法比Prim算法还是要精简点的。
3. 前置文章
- 浅入数据结构 “堆” - 实现和理论
- 开始熟悉 “二叉树” 的数据结构
- 队列 和 符号表 两种数据结构的实现
- 队列的进阶结构-优先队列
- 2-3树思想与红黑树的实现与基本原理
- B树和B+树的实现原理阐述
- 图的基本原理和API实现
- 有向图与拓扑排序的实现原理与基本实现
4. ES8 如何使用?
快来看看这篇好文章吧~~!! 😊👉(全篇详细讲解)ElasticSearch8.7 搭配 SpringDataElasticSearch5.1 的使用

