【优选算法必刷100题】第003~004题（双指针算法）：快乐数和盛水最多的容器

用户11915063

发布于 2025-11-20 09:55:01

330

003.快乐数

题目链接：

202. 快乐数 - 力扣（LeetCode）

题目描述：

题目示例：

题目分析：

为了方便叙述，将【对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和】这一个操作记为 x 操作

当我们读到下面这句话的时候，我们就可以清晰地将这道题分为两种情况

情况一：一直在 1 中死循环，即 1 -> 1 -> 1- > 1……
情况二：在历史的数据中死循环，但始终变不到 1

简单证明：

1.经过依次变化之后的最大值 9^2*10=810 (2^31-1=2147483647。选一个更大的最大9999999999），也就是变化的区间在【1，810】之间
2.根据【鸽巢原理】，一个数变化 811 次之后，必然会形成一个循环；
3.所以，变化的过程最终会走到一个圈里面，因此可以用【快慢指针】来解决

解法：（快慢指针）

算法思路：

根据上述的题目分析，我们可以知道，当重复执行 x 的时候，数据会陷入到一个【循环】之中。而【快慢指针】有一个特性，就是在一个圆圈里，快指针总是会追上慢指针的，也就是说他们总会相遇在一个位置上。如果相遇的位置的值是 1 ，那么这个数一定是快乐数；如果相遇的位置不是 1 的话，那么就不是快乐数。

补充：如何求一个数n每个位置上的数字的平方和

1.把数 n 的每一位的数都提取出来，循环迭代以下步骤

1.1 int t = n % 10 提取个位；
1.2 n /= 10 干掉个位

直到 n 的值变为 0；

2.提取每一位的时候，用一个变量 tmp 记录这一位的平方与之前提取位数的平方和

tmp = tmp + t * t

C++代码演示：

class Solution {
    int bitsum(int n)
    {
        int sum=0;
        while(n)
        {
            int t=n%10;
            sum+=t*t;
            n/=10;
        }
        return sum;
    }
public:
    bool isHappy(int n) {
        int slow=n;
        int fast=bitsum(n);
        while(slow!=fast)
        {
            slow=bitsum(slow);
            fast=bitsum(bitsum(fast));
        }
        return slow==1;
    }
};

算法总结&&笔记展示：

博主笔记（字迹有点丑，请大家见谅）：

04.盛水最多的容器

题目链接：

11. 盛最多水的容器 - 力扣（LeetCode）

题目描述：

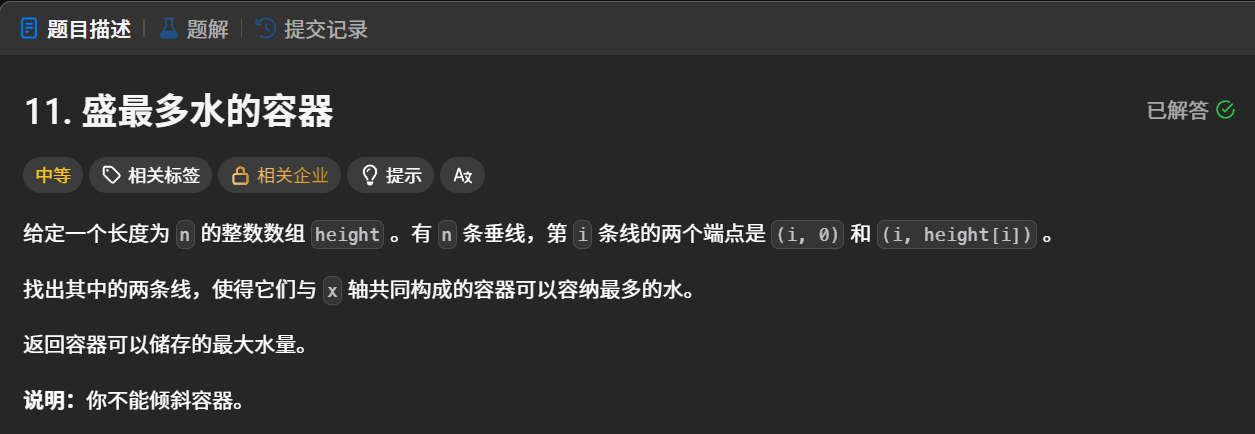
题目示例：

解法：双指针（对撞指针)

算法思路：

设两个指针 left ，right 分别指向容器的左右两个端点，此时容器的容积：

v = （right - left）* min（height[right]，height[left]）

容器的左边界为 height[left]，右边界为 height[right]

为了方便叙述，我们假设【左边边界】小于【右边边界】。

如果此时我们固定一个边界，改变另一个边界，水的容积会有如下变化形式：

容器的宽度一定变小
由于左边界较小，决定了水的高度。如果改变左边界，新的水面高度不确定，但是一定不会超过右边的柱子高度，因此容器的容积可能会增大
如果改变右边界，无论右边界移动到哪里，新的水面高度一定不会超过左边界，也就是不会超过现在的水面高度，但是由于容器的宽度减小，因此容器的容积是一定会变小的

由此可见，左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界，继续去判断下一个右边界。（那在本题里就是先比较左右谁小，如果左边小就left++，右边小就right--）

当我们不断重复上述过程，每次都可以舍去大量不必要的枚举过程，直到 left 与 right 相遇。期间产生的所有的容积里面的最大值，就是最终答案

C++代码演示：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left=0,right=height.size()-1,ret=0;
        while(left<right)
        {
            int v=min(height[left],height[right])*(right-left);
            ret=max(ret,v);
            if(height[left]<height[right]) left++;
            else right--;
        }
        return ret;
    }
};