【优选算法必刷100题】第007~008题（双指针算法）：三数之和，四数之和

用户11915063

发布于 2025-11-20 09:55:50

680

007.三数之和

题目链接：

15. 三数之和 - 力扣（LeetCode）

题目描述：

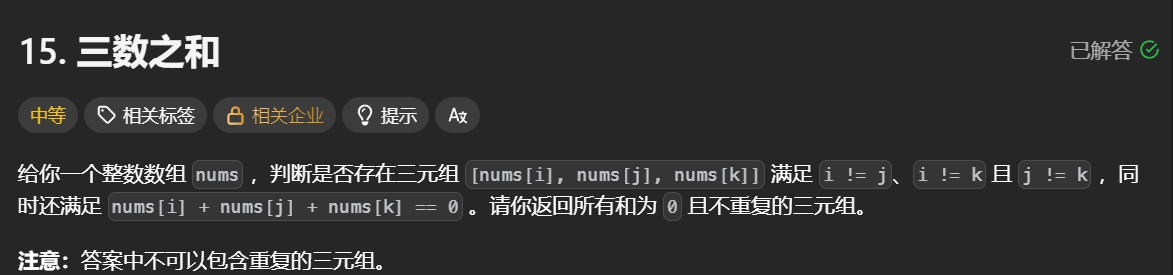
题目示例：

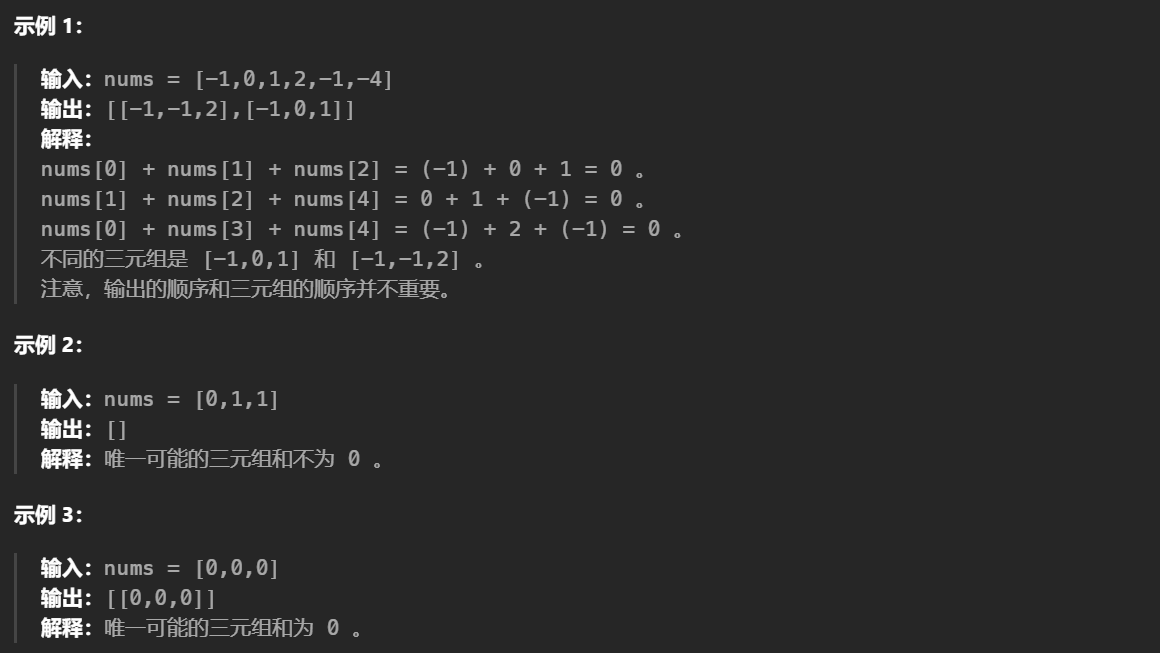
解法：（排序+双指针）

--暴力算法就不讲了，（排序+暴力+set去重）。时间复杂度过高，肯定过不了。

算法思路：

本题与两数之和为s类似，是非常经典的面试题

与两数之和稍微不同的是，题目中要求找到所有【不重复】的三元组。那我们可以利用在两数之和为s那里的双指针思想，来对我们暴力枚举进行优化：

先排序
然后固定一个数a
在这个数后面的区间内，使用【双指针算法】快速找到两个数之和等于 -a 即可。

但是我们需要注意的是，这道题里面需要有【去重】操作！

找到一个结果之后，不要停，left++，right-- 缩小区间后， left 和 right 指针也要【跳过重复】的元素；

当使用完一次双指针算法之后，固定的 a 也要 【跳过重复】的元素

C++代码演示：

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) 
    {
        vector<vector<int>> ret;
        //排序
        sort(nums.begin(),nums.end());
        //利用双指针算法
        int n=nums.size();
        for(int i=0;i<n;)
        {
            if(nums[i]>0) break;
            int left=i+1,right=n-1,target=-nums[i];
            while(left<right)
            {
                int sum=nums[left]+nums[right];
                if(sum>target) right--;
                else if(sum<target) left++;
                else
                {
                    ret.push_back({nums[i],nums[left],nums[right]});
                    left++,right--;
                    //去重操作left和right
                    while(left<right&&nums[left]==nums[left-1]) left++;
                    while(right<right&&nums[right]==nums[right+1]) right--;
                }
            }
            //去重i
            i++;
            while(i<n&&nums[i]==nums[i-1]) i++;
        }
        return ret;
    }
};

算法总结&&笔记展示：

博主笔记（字迹有点丑，请大家见谅）：

008.四数之和

题目链接：

18. 四数之和 - 力扣（LeetCode）

题目描述：

题目示例：

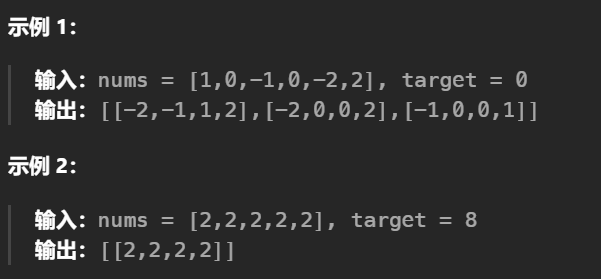
解法：（排序+双指针）

--暴力解法这里还是不提了，肯定超时。

算法思路：

依次固定一个数 a；
在这个数 a 的后面区间上，利用【三数之和】找到三个数，使这三个数的和等于 target-a 即可

C++代码演示：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) 
    {
        vector<vector<int>> ret;
        //排序
        sort(nums.begin(),nums.end());
        //利用双指针解决问题
        int n=nums.size();
        for(int i=0;i<n;)//固定数a
        {
            for(int j=i+1;j<n;)//固定数b
            {
                int left=j+1,right=n-1;
                long long aim=(long long)target-nums[i]-nums[j];
                while(left<right)
                {
                    int sum=nums[left]+nums[right];
                    if(sum>aim) right--;
                    else if(sum<aim) left++;
                    else
                    {
                        ret.push_back({nums[i],nums[j],nums[left++],nums[right--]});
                        //去重1
                        while(left<right&&nums[left]==nums[left-1]) left++;
                        while(left<right&&nums[right]==nums[right+1]) right--;
                    }
                }
                //去重2
                j++;
                while(j<n&&nums[j]==nums[j-1]) j++;
            }
            //去重3
            i++;
            while(i<n&&nums[i]==nums[i-1]) i++;
        }    
        return ret;
    }
};

算法总结&&笔记展示：

博主笔记（字迹有点丑，请大家见谅）：

往期回顾：

【优选算法必刷100题】第001~002题（双指针算法）：移动零、复写零问题

【优选算法必刷100题】第003~004题（双指针算法）：快乐数和盛水最多的容器

【优选算法必刷100题】第005~006题（双指针算法）：有效三角形的个数和查找总价值为目标值的两个商品

总结：本篇博客介绍了LeetCode中三数之和与四数之和问题的解题思路。通过排序+双指针算法优化暴力解法，重点讲解了去重操作的实现方法。对于三数之和，固定一个数后用双指针在剩余区间寻找两数之和；四数之和则通过固定两个数后转化为三数之和问题。如果文章对你有帮助的话，欢迎评论，点赞，收藏加关注，感谢大家的支持

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-10-06，如有侵权请联系 cloudcommunity@tencent.com 删除

笔记