2025-12-03：计数质数间隔平衡子数组。用go语言，给定一个整数数组 nums 和一个整数 k。请计算数组中有多少个连续且

福大大架构师每日一题

发布于 2025-12-19 09:33:52

530

文章被收录于专栏：福大大架构师每日一题福大大架构师每日一题

2025-12-03：计数质数间隔平衡子数组。用go语言，给定一个整数数组 nums 和一个整数 k。请计算数组中有多少个连续且非空的子序列满足下面两个条件：

1. 子序列中至少包含两个质数；
2. 该子序列里所有质数中的最大值与最小值之差不超过 k。

这里“子序列”指的是数组中位置相邻的一段元素（即常说的子数组）。质数指大于 1 且只有 1 和自身两个约数的正整数。返回符合上述条件的子序列数量。

1 <= nums.length <= 50000。

1 <= nums[i] <= 50000。

0 <= k <= 50000。

输入：nums = [2,3,5,7], k = 3。

输出：4。

解释：

质数间隔平衡子数组有：

[2,3]：包含 2 个质数（2 和 3），最大值 - 最小值 = 3 - 2 = 1 <= k.

[2,3,5]：包含 3 个质数（2，3 和 5），最大值 - 最小值 = 5 - 2 = 3 <= k.

[3,5]：包含 2 个质数（3 和 5），最大值 - 最小值 = 5 - 3 = 2 <= k.

[5,7]：包含 2 个质数（5 和 7），最大值 - 最小值 = 7 - 5 = 2 <= k.

因此，答案为 4。

题目来自力扣3589。

算法过程详解

该Go语言程序用于统计满足特定条件的连续子数组（子序列）数量。以下是大体过程的详细分步描述：

1. 质数预计算（初始化阶段）

• 程序使用埃拉托斯特尼筛法预计算所有小于50,001的质数。全局数组np用于标记非质数（np[i]为true表示i不是质数）。
• 筛法从2开始遍历到√mx，对每个质数i，标记其所有倍数（从i*i开始）为非质数。这一步确保在后续处理中能以O(1)时间判断任意数是否为质数。

2. 滑动窗口遍历主逻辑

函数primeSubarray使用双指针（滑动窗口） 结合单调队列来动态维护窗口内的质数极值：

• 初始化：
- • left：窗口左边界，初始为0。
- • last和last2：分别记录当前窗口内最近一个和倒数第二个质数的位置，初始为-1。
- • minQ和maxQ：单调队列（双端队列），分别维护当前窗口内质数索引的递增（最小值队列）和递减（最大值队列）顺序。
• 遍历数组（右指针扩张）：
- • 对每个元素nums[i]，若它是质数（!np[x]为真）：
  1. 1. 更新质数位置： last2记录上一个质数位置（last），last更新为当前索引i。这确保窗口内至少有两个质数时，last2有效。
  2. 2. 维护单调队列：
    - • 最小值队列minQ：从队尾移除所有对应质数大于等于当前质数的索引，保持队列严格递增。
    - • 最大值队列maxQ：从队尾移除所有对应质数小于等于当前质数的索引，保持队列严格递减。然后将当前索引i加入两队。
  3. 3. 调整窗口左边界（收缩）：若当前窗口内最大质数与最小质数之差（即nums[maxQ[0]] - nums[minQ[0]]）超过k，则右移左边界left。同时，清理minQ和maxQ中队首小于left的索引（这些索引已离开窗口）。
• 统计有效子数组：每处理一个元素后（无论是否为质数），若窗口内至少有两个质数（last2 ≠ -1），则计算以i结尾的有效子数组数量： 左边界范围是[left, last2]，因为子数组必须包含last2和last两个质数。因此，答案增加last2 - left + 1。

3. 结果返回

• 遍历结束后，返回累加值ans，即所有满足条件的子数组数量。

复杂度分析

• 时间复杂度：
- • 质数筛预计算：O(mx log log mx) ≈ O(50,000 log log 50,000)，可视为常数级。
- • 主遍历：数组长度为n，每个元素最多被加入/移除单调队列一次，均摊操作O(1)。因此总时间复杂度为 O(n)。
• 空间复杂度：
- • 固定数组np占用O(mx) ≈ O(50,000)，为常数空间。
- • 单调队列minQ和maxQ最坏情况下存储O(n)个索引。因此总额外空间复杂度为 O(n)。

关键点总结

• 通过质数筛实现O(1)质数判断，避免每次重复计算。
• 单调队列高效维护滑动窗口内的极值，确保质数差约束的实时检查。
• 利用last2记录倒数第二个质数位置，直接确定有效左边界范围，避免暴力枚举。

Go完整代码如下：

package main

import (
    "fmt"
)

const mx = 50_001

var np = [mx]bool{1: true} // 1 不是质数

func init() {
    for i := 2; i*i < mx; i++ {
        if !np[i] {
            for j := i * i; j < mx; j += i {
                np[j] = true
            }
        }
    }
}

func primeSubarray(nums []int, k int) (ans int) {
    var minQ, maxQ []int
    last, last2 := -1, -1
    left := 0

    for i, x := range nums {
        if !np[x] {
            // 1. 入
            last2 = last
            last = i

            forlen(minQ) > 0 && x <= nums[minQ[len(minQ)-1]] {
                minQ = minQ[:len(minQ)-1]
            }
            minQ = append(minQ, i)

            forlen(maxQ) > 0 && x >= nums[maxQ[len(maxQ)-1]] {
                maxQ = maxQ[:len(maxQ)-1]
            }
            maxQ = append(maxQ, i)

            // 2. 出
            for nums[maxQ[0]]-nums[minQ[0]] > k {
                left++
                if minQ[0] < left {
                    minQ = minQ[1:]
                }
                if maxQ[0] < left {
                    maxQ = maxQ[1:]
                }
            }
        }

        // 3. 更新答案
        ans += last2 - left + 1
    }

    return
}

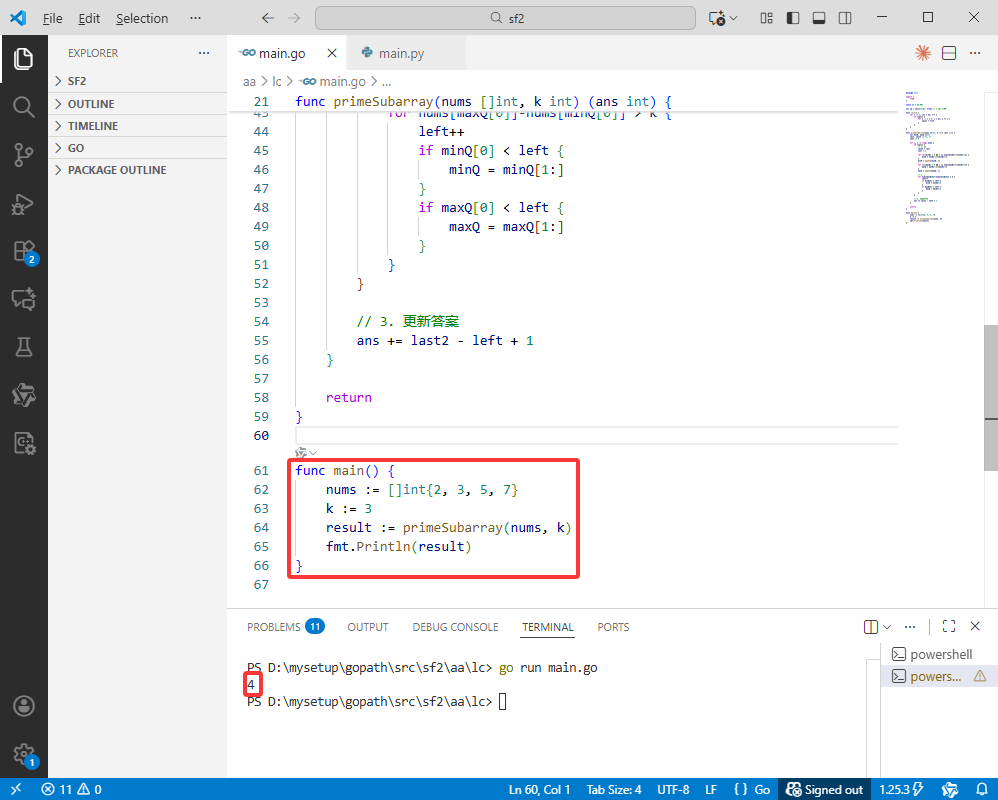
func main() {
    nums := []int{2, 3, 5, 7}
    k := 3
    result := primeSubarray(nums, k)
    fmt.Println(result)
}

Python完整代码如下：

# -*-coding:utf-8-*-

from typing import List
from collections import deque

# 预处理质数
MX = 50001
np = [False] * MX
np[0] = np[1] = True  # 0 和 1 不是质数

for i in range(2, int(MX ** 0.5) + 1):
    if not np[i]:
        for j in range(i * i, MX, i):
            np[j] = True

def primeSubarray(nums: List[int], k: int) -> int:
    ans = 0
    min_q = deque()  # 单调递增队列（最小值的索引）
    max_q = deque()  # 单调递减队列（最大值的索引）
    last = -1  # 最近一个质数的索引
    last2 = -1  # 倒数第二个质数的索引
    left = 0  # 窗口左边界
    
    for i, x in enumerate(nums):
        if not np[x]:  # x 是质数
            # 1. 更新质数索引
            last2 = last
            last = i
            
            # 维护最小值的单调递增队列
            while min_q and x <= nums[min_q[-1]]:
                min_q.pop()
            min_q.append(i)
            
            # 维护最大值的单调递减队列
            while max_q and x >= nums[max_q[-1]]:
                max_q.pop()
            max_q.append(i)
            
            # 2. 调整窗口左边界，确保窗口内最大最小差值 <= k
            while nums[max_q[0]] - nums[min_q[0]] > k:
                left += 1
                if min_q[0] < left:
                    min_q.popleft()
                if max_q[0] < left:
                    max_q.popleft()
        
        # 3. 更新答案（累加以当前元素结尾的有效子数组数量）
        ans += max(0, last2 - left + 1)
    
    return ans

if __name__ == "__main__":
    nums = [2, 3, 5, 7]
    k = 3
    result = primeSubarray(nums, k)
    print(result)  # 输出结果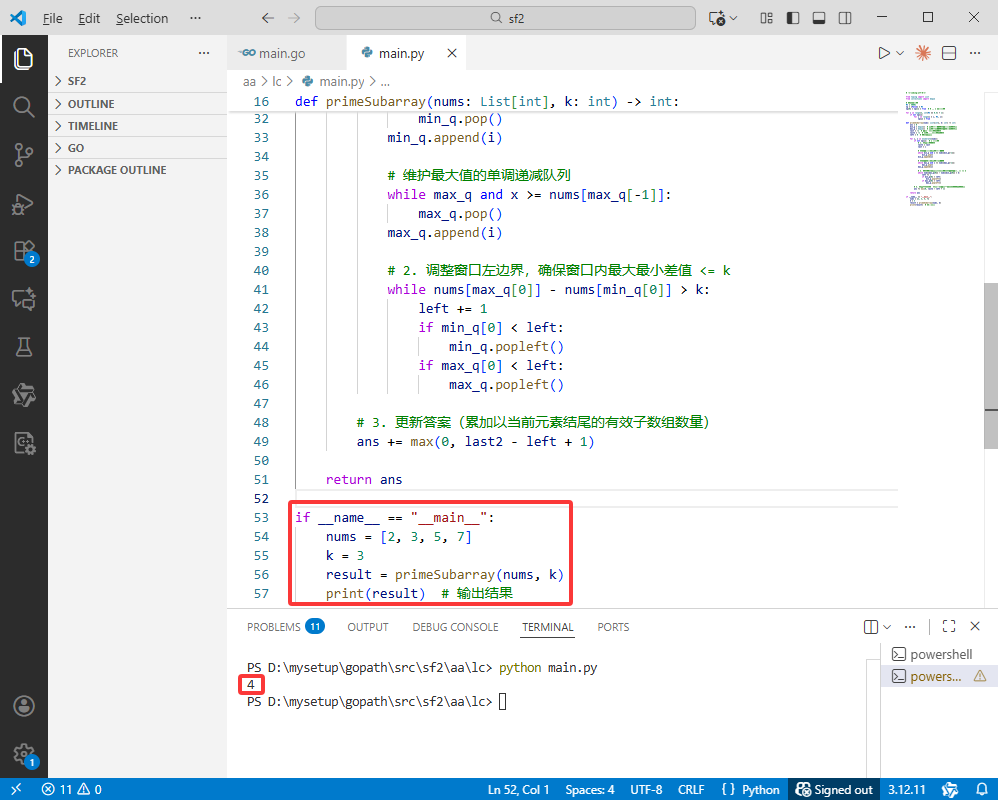

C++完整代码如下：

#include <iostream>
#include <vector>
#include <deque>
#include <algorithm>
using namespace std;

constint MX = 50001;
bool np[MX] = {false};

// 初始化质数筛
void init() {
    np[0] = np[1] = true;  // 0和1不是质数
    for (int i = 2; i * i < MX; i++) {
        if (!np[i]) {
            for (int j = i * i; j < MX; j += i) {
                np[j] = true;
            }
        }
    }
}

int primeSubarray(vector<int>& nums, int k) {
    int ans = 0;
    deque<int> minQ;  // 单调递增队列（最小值的索引）
    deque<int> maxQ;  // 单调递减队列（最大值的索引）
    int last = -1;    // 最近一个质数的索引
    int last2 = -1;   // 倒数第二个质数的索引
    int left = 0;     // 窗口左边界

    for (int i = 0; i < nums.size(); i++) {
        int x = nums[i];
        if (!np[x]) {  // x是质数
            // 1. 更新质数索引
            last2 = last;
            last = i;

            // 维护最小值的单调递增队列
            while (!minQ.empty() && x <= nums[minQ.back()]) {
                minQ.pop_back();
            }
            minQ.push_back(i);

            // 维护最大值的单调递减队列
            while (!maxQ.empty() && x >= nums[maxQ.back()]) {
                maxQ.pop_back();
            }
            maxQ.push_back(i);

            // 2. 调整窗口左边界，确保窗口内最大最小差值 <= k
            while (nums[maxQ.front()] - nums[minQ.front()] > k) {
                left++;
                if (!minQ.empty() && minQ.front() < left) {
                    minQ.pop_front();
                }
                if (!maxQ.empty() && maxQ.front() < left) {
                    maxQ.pop_front();
                }
            }
        }

        // 3. 更新答案（累加以当前元素结尾的有效子数组数量）
        if (last2 >= left) {
            ans += last2 - left + 1;
        }
    }

    return ans;
}

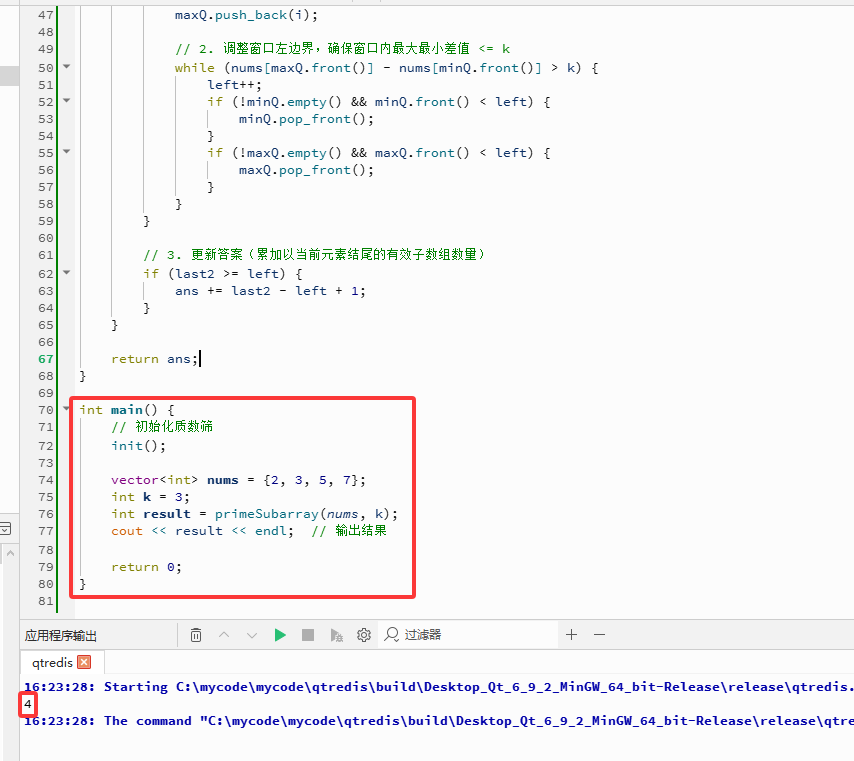
int main() {
    // 初始化质数筛
    init();

    vector<int> nums = {2, 3, 5, 7};
    int k = 3;
    int result = primeSubarray(nums, k);
    cout << result << endl;  // 输出结果

    return0;
}