七大基于比较的常见排序算法
七大基于比较的常见排序算法
景画
发布于 2025-12-19 13:42:37
发布于 2025-12-19 13:42:37
一. 常见排序算法
算法: 危险而迷人的数字炼金术 接下来我们会一一介绍下面常见的排序算法
二. 直接插入排序
1. 算法原理
1.给出一组无序数组时, 从前先后遍历该数组, 同时因为只有一个数据时默认是有序的, 因此从下标1开始遍历 2.遍历过程中, 把当前i下标的值 arri 用临时变量tmp储存起来, 并设定第二个循环从 i-1 位置, 从后往前开始比较 tmp 中的值, 大于则将 arrj 往前移一位, 以此类推, 否则直接跳出该循环 3.循环结束或者跳出循环后, 需要把tmp中的值赋值到 j+1 位置
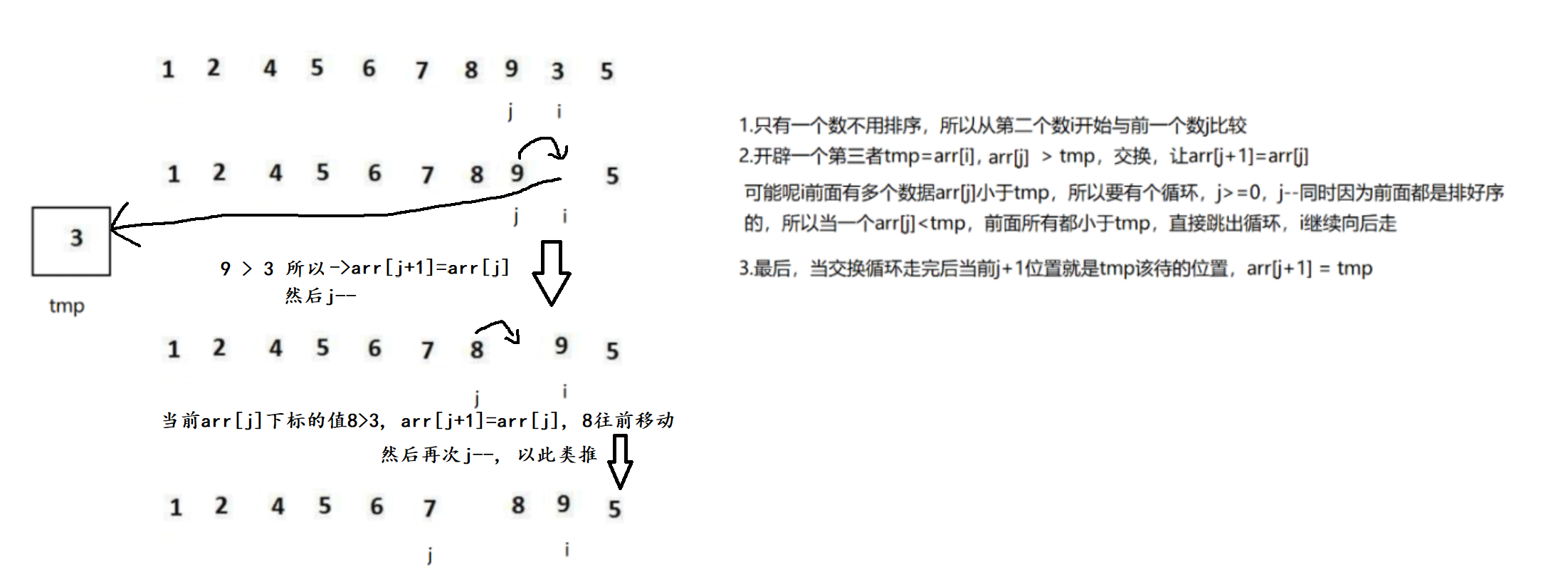
在这里插入图片描述
2. 代码
/**
* Created with IntelliJ IDEA.
* Description:
* User: ran
* Date: 2025-09-11
* Time: 15:58
*/
public class Sort {
public void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i - 1;
for (; j >= 0; j--) {
if (array[j] > tmp) {
array[j + 1] = array[j];
}else {
break;
}
}
array[j + 1] = tmp;
}
}
}3. 测试图
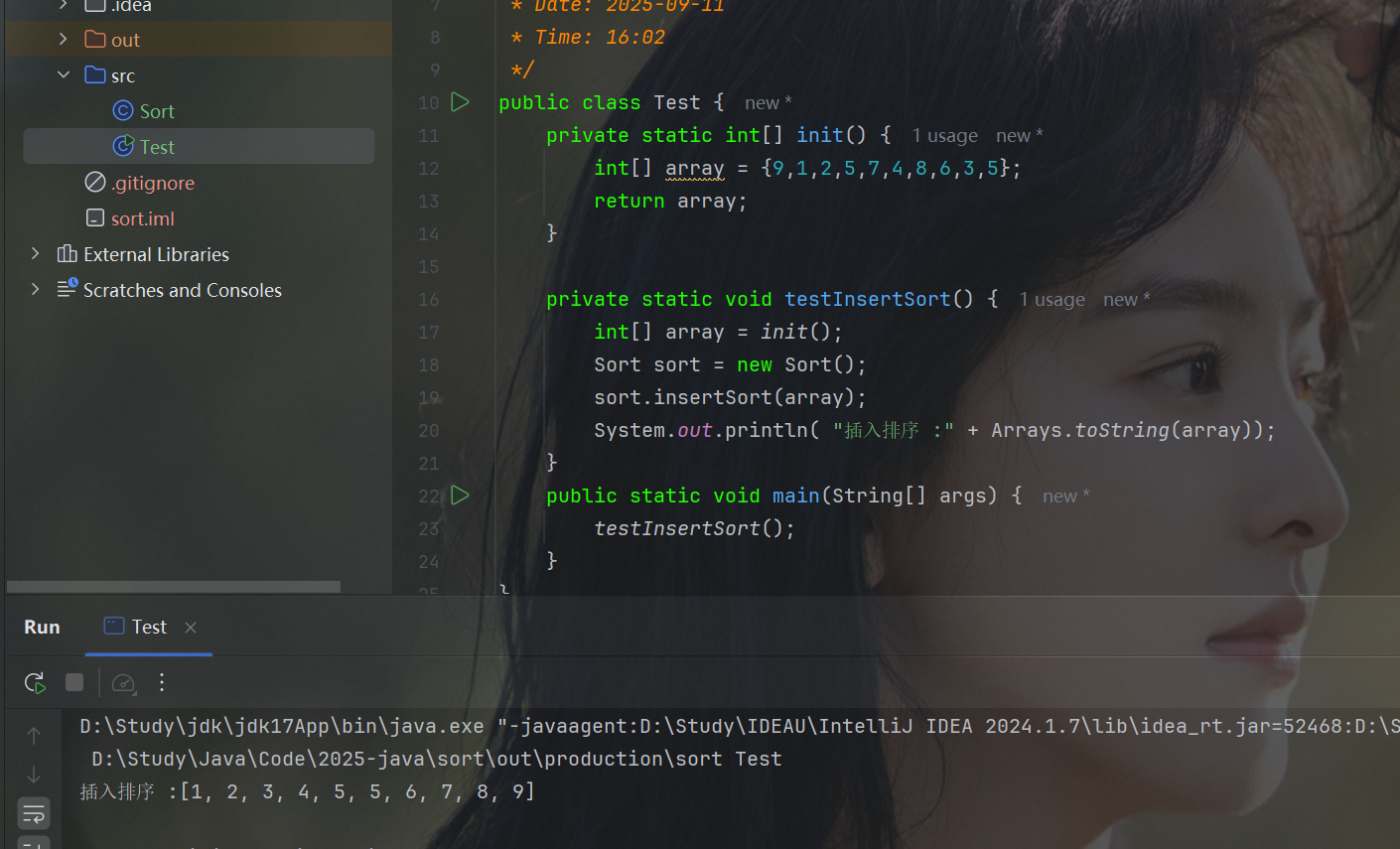
在这里插入图片描述
4. 复杂度
1.时间复杂度:O(N^2) 最好情况(顺序排列)能达到O(N) 2.空间复杂度:O(1) 3.稳定性: 稳定
三. 希尔排序
1. 算法原理
1.先分组: 按数组的长度每次除2来分组, 且最后一组必须是1 2.分完组之后调用插入排序, 但这里这插入排序的 i 每次都从gap开始, j 每次都从 (i - gap) 开始, 且每次 j 都减去gap的长度, 每次比较仍然是将 i 下标的值放入临时变量 tmp 中 3.将 j 下标的值与 tmp 比较, 大于则放到 (j + gap) 位置, 同时 j 向前移动 gap 个长度, 知道小于0 越界, 小于则直接 break 跳出循环 4.循环结束则将 tmp 的值赋值到 (j + gap) 位置
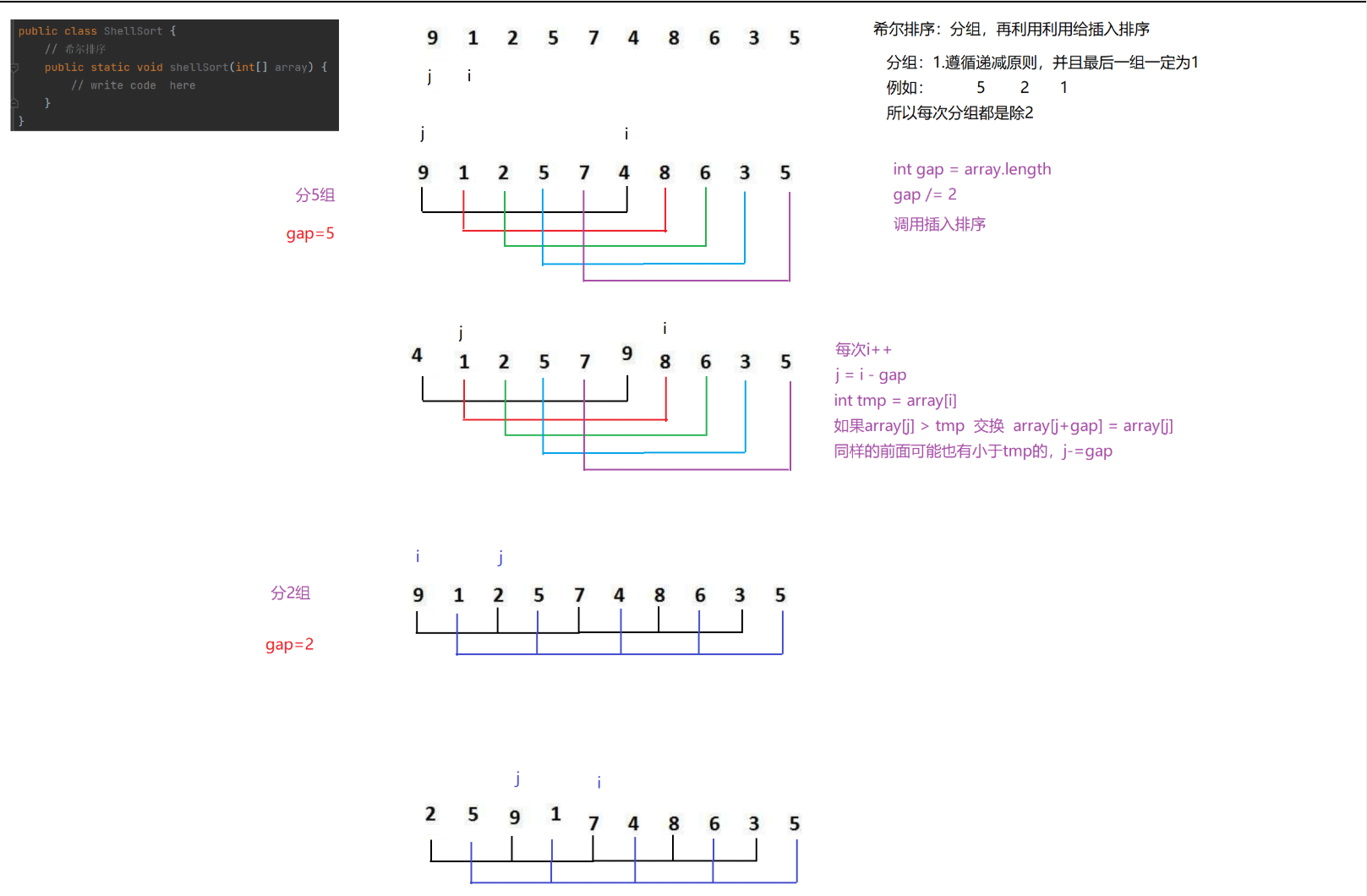
在这里插入图片描述
2. 代码
public void shellSort(int[] array) {
int gap = array.length;
while (gap > 1) {
gap /= 2;
insert(array,gap);
}
}
private void insert(int[] array, int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i - gap;
for (; j >= 0; j -= gap) {
if (array[j] > tmp) {
array[j + gap] = array[j];
}else {
break;
}
}
array[j + gap] = tmp;
}
}3. 测试图
在这里插入图片描述
4. 复杂度
1.时间复杂度:O(N^1.25 至 1.6N^1.25) 2.空间复杂度:O(1) 3.稳定性: 不稳定
四. 直接选择排序
1. 算法原理
i 从0位置开始, 遍历整个数组, 找到最小的那个数, 该数就是 i 的位置, 然后交换这两个位置的数值, 以此类推, 当然也可以从后往前找最大值

在这里插入图片描述
2. 代码
public void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int min = array[i];
int index = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < min) {
min = array[j];
index = j;
}
}
swap(array,i,index);
}
}3. 测试图
在这里插入图片描述
4. 优化
1.设置左右下标 left 与 right, 遍历数组, 同时找最大值下标 minIndex 和最小值下标 maxIndex 2.同时进行 mindex 与 left 交换, maxIndex 与 right 交换, 然后 left++, right– 3.每次寻找都要从 left,right 的范围之中去寻找 4.但是当 maxIndex == left 时, 最小值交换后会导致 left 的值发生改变, 所以需要特殊处理, 把 maxIndex 改为 minIndex

在这里插入图片描述
5. 代码
public void selectSort2(int[] array) {
int left = 0;
int right = array.length - 1;
for (;left < right; left++,right--) {
int min = array[left];
int minIndex = left;
int max = array[right];
int maxIndex = right;
for (int j = left; j < right; j++) {
if (array[j] < min) {
min = array[j];
minIndex = j;
}
if (array[j] > max) {
max = array[j];
maxIndex = j;
}
}
swap(array,left,minIndex);
if (maxIndex == left) {
maxIndex = minIndex;
}
swap(array,right,maxIndex);
}
}6. 测试图

在这里插入图片描述
7. 复杂度
1.时间复杂度:O(N^2) 2.空间复杂度:O(1) 3.稳定性: 不稳定
五. 堆排序
1. 算法原理
堆排序的前提就是创建一个堆, 从小到大排序就创建大根堆, 从大到小排序就创建小根堆, 首尾元素交换, 然后通过向下调整为大根堆, 首元素与末尾前一个元素交换, 以此类推
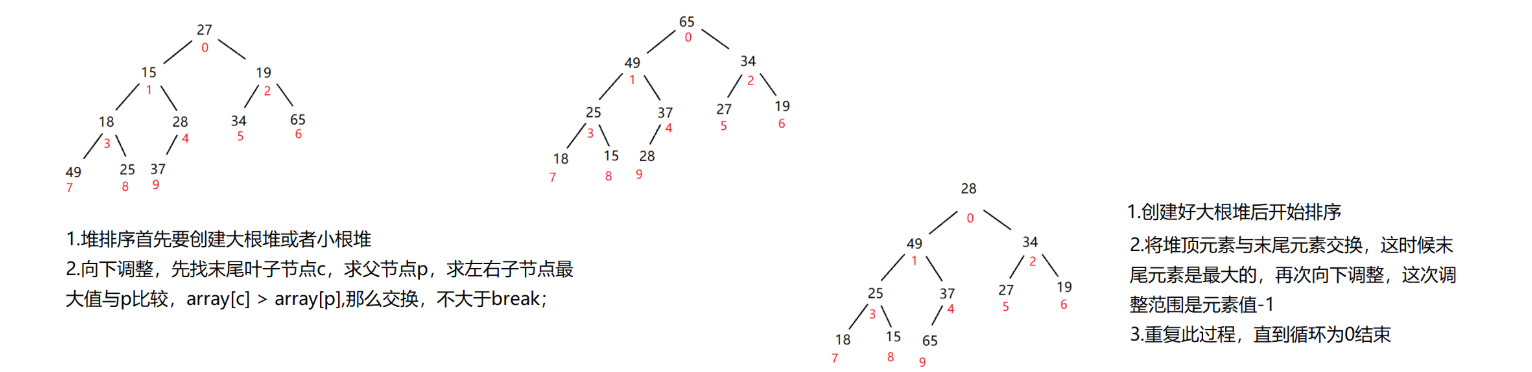
在这里插入图片描述
2. 代码
public void heapSort(int[] array) {
int tail = array.length - 1;
createHeap(array);
while (tail > 0) {
swap(array,0,tail);
tail--;
down(array,0,tail);
}
}
private void createHeap(int[] array) {
int parent = (array.length - 1) / 2;
while (parent >= 0) {
down(array,parent,array.length - 1);
parent--;
}
}
private void down(int[] array, int parent,int limit) {
int child = parent * 2 + 1;
while (child <= limit) {
if ((child + 1) < limit && array[child + 1] > array[child]) {
child++;
}
if (array[parent] < array[child]) {
swap(array,parent,child);
}else {
break;
}
parent = child;
child = parent * 2 + 1;
}
}3. 测试图
在这里插入图片描述
4. 复杂度
1.时间复杂度:O(N*logN) 2.空间复杂度:O(1) 3.稳定性: 不稳定
六. 快速排序(典中典)
1. Hoare法
(1) 算法原理
每次先设定left下标的值为基准 pivot , right然后先从后往前遍历, 找到比 pivot 小的数就停下来, left再从前往后遍历, 找到比 pivot 大的数 就停下来, 然后交换 left下标与 right下标的值, 以此类推, 直到 left >= right停止, 该相遇位置, 就是原来 pivot 该待的位置, 再次交换后基准值位置就确定了下来, 我们可以发现: pivot左面都是小于基准值的数, 右面都是大于或等于基准值的数(或者pivot左面都是小于/等于基准值的数, 右面都是大于基准值的数)

在这里插入图片描述
(2) 代码
public void quickSort(int[] array) {
quick(array,0,array.length - 1);
}
private void quick(int[] array, int left, int right) {
if (left >= right) {
return;
}
// 获取pivot值
int pivot = partition(array,left,right);
// 递归左
quick(array,left,pivot - 1);
// 递归右
quick(array,pivot + 1,right);
}
private int partition(int[] array, int left, int right) {
int pivot = left;
while (left < right) {
while (left < right && array[right] >= array[pivot]) {
right--;
}
while (left < right && array[left] <= array[pivot]) {
left++;
}
// 当前 left 下标值是大于基准值的, right 下标值是小于基准值的
swap(array,left,right);
}
// 最后将基准值放到 left 与 right 相遇处
swap(array,pivot,left);
return right;
}(3) 疑问
1.为什么要先从后往前找呢? 我先从前往后找不行吗? 答: 不行, 会不满足pivot左面都是小于基准值的数, 右面都是大于或等于基准值的数(或者pivot左面都是小于/等于基准值的数, 右面都是大于基准值的数)

在这里插入图片描述
2.在partition这个函数中 arrayright >= arraypivot 与 arrayleft <= arraypivot, 这两个条件, 必须带等号吗? 都去掉可不可以? 去掉一个可不可以?
答: 都去掉是不行的会陷入死循环, 去掉一个是可以的

在这里插入图片描述
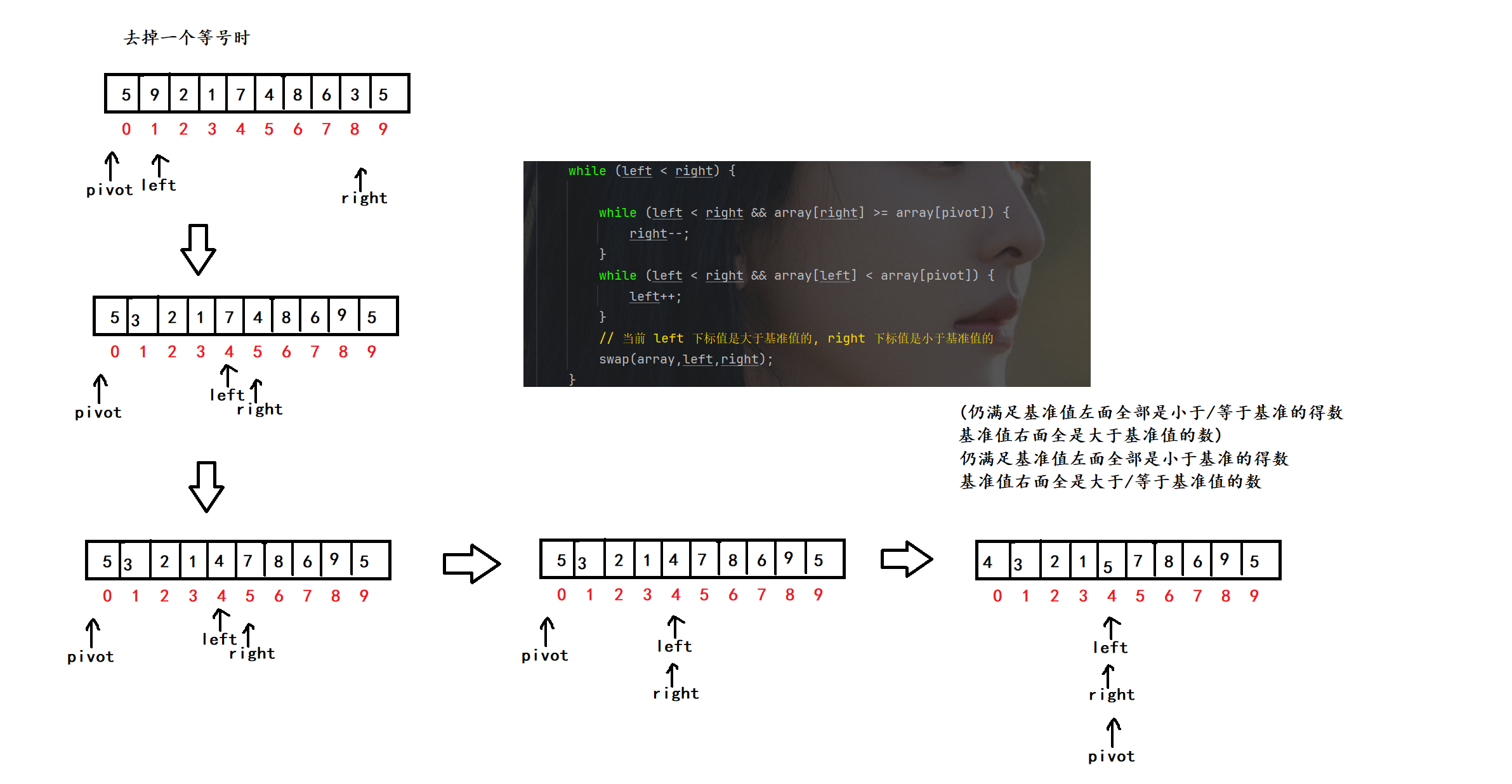
在这里插入图片描述
(4) 测试图

在这里插入图片描述
2. 挖坑法(最常考, 最重要)
(1) 算法原理
先以left为基准值, 把基准值放入到临时数组tmp中, left 下标位置相当于为空, 先从右往左遍历找到小于该基准值的下标 right, 将值放入到 left 下标, 这时 right 下标相当于空出一个位置, left再从左向右遍历, 找到比基准值大的值, 放入到right 下标, 以此类推, 直到 left 与 right 相遇, 基准值放入到相遇的下标位置 , 找基准值 pivot 的方法与 Hoare 法一致

在这里插入图片描述
(2) 代码
public void quickSort(int[] array) {
quick(array,0,array.length - 1);
}
private void quick(int[] array, int left, int right) {
if (left >= right) {
return;
}
// 获取pivot值
int pivot = partition(array,left,right);
// 递归左
quick(array,left,pivot - 1);
// 递归右
quick(array,pivot + 1,right);
}
private int partition(int[] array, int left, int right) {
int tmp = array[left];
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
while (left < right && array[left] < tmp) {
left++;
}
array[right] = array[left];
}
// 最后将基准值放到 left 与 right 相遇处
array[left] = tmp;
return right;
}(3) 测试图
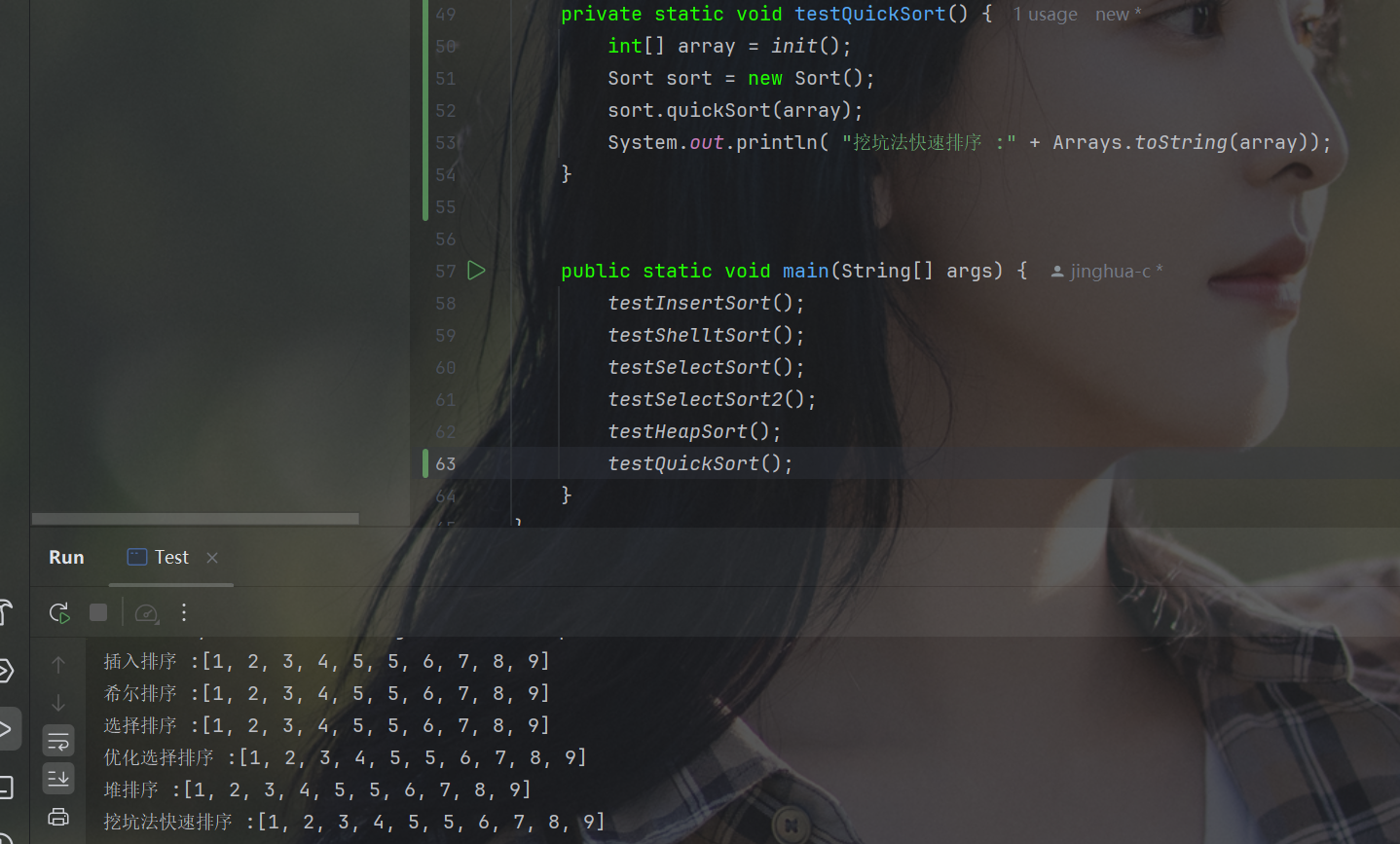
在这里插入图片描述
3. 双指针法
(1) 算法原理
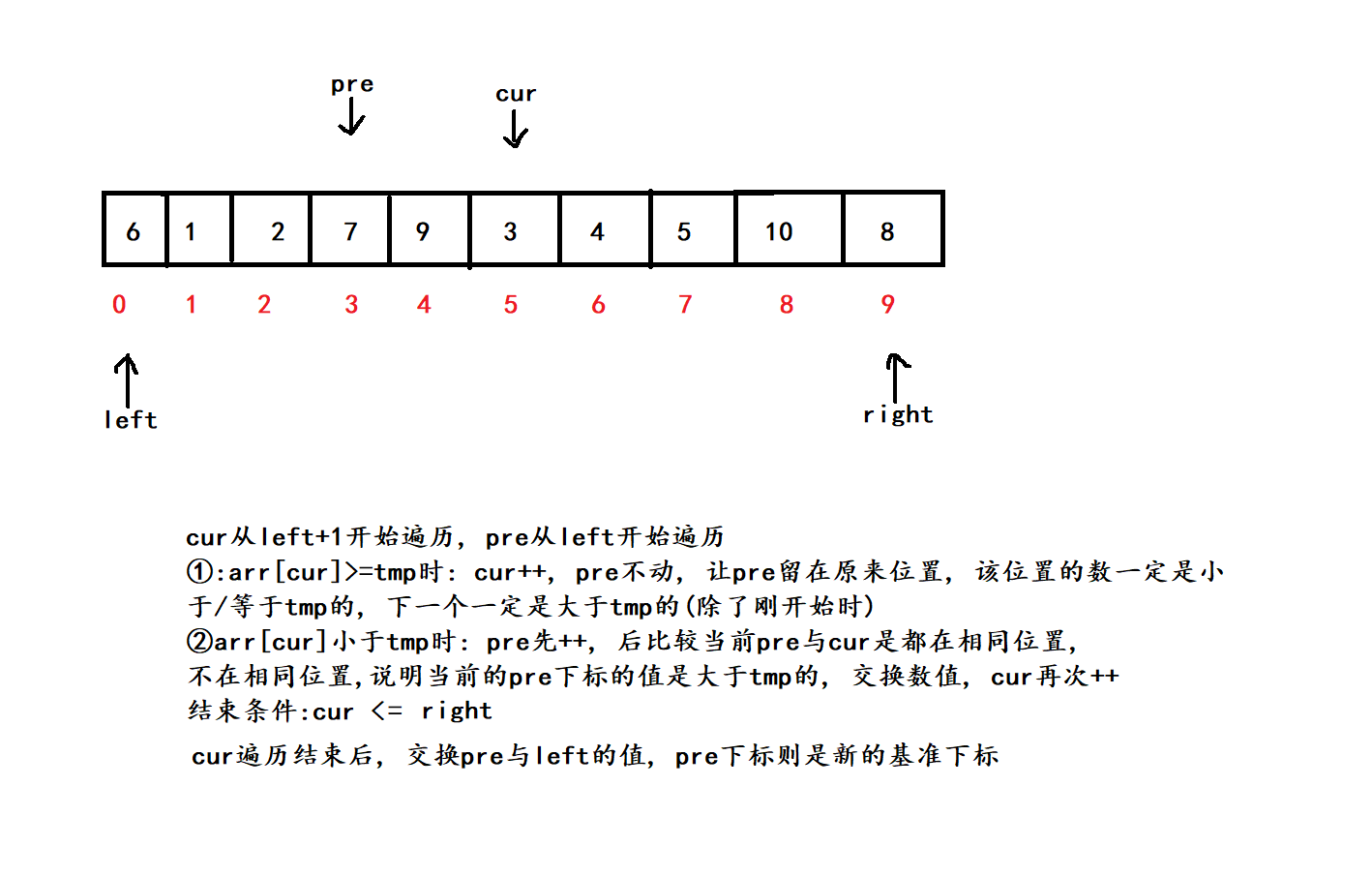
在这里插入图片描述
(2) 代码
private int partitionPreAndafter(int[] array, int left, int right) {
int tmp = array[left];
int pre = left;
int cur = left + 1;
while (cur <= right) {
if (array[cur] < tmp && ++pre != cur) {
swap(array,pre,cur);
}
cur++;
}
swap(array,pre,left);
return pre;
}(3) 测试图
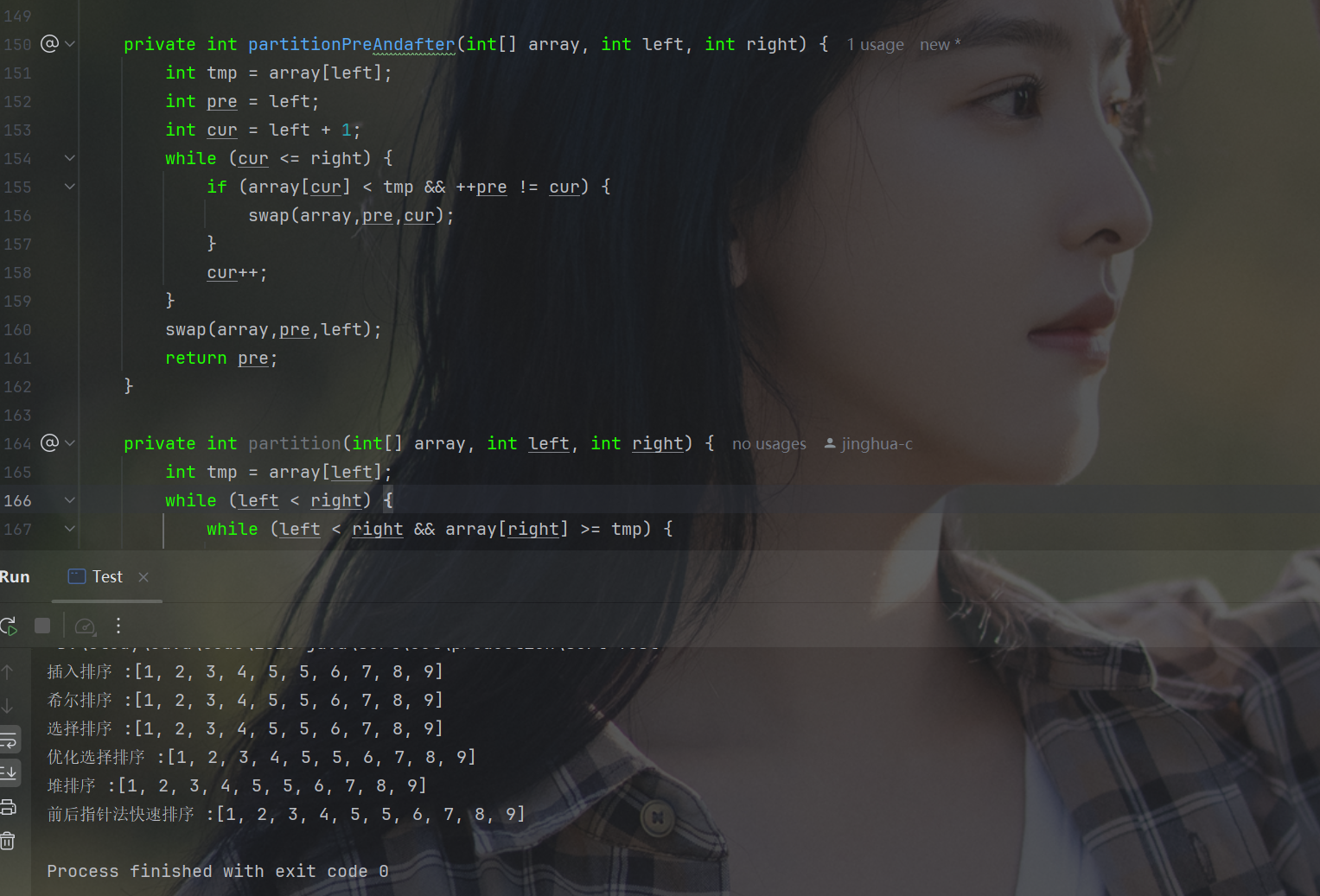
在这里插入图片描述
4. 非递归算法
(1) 算法原理
非递归主要中的是模拟每次递归过程中的新写的start与end如何找到, 这里可以借助一个容器-栈

在这里插入图片描述
(2) 代码
public void quickNoRecursive(int[] array) {
int start = 0;
int end = array.length - 1;
// 获取pivot值
int pivot = partition(array,start,end);
// 加入左侧新的s与e
Stack<Integer> stack = new Stack<>();
if (pivot > start + 1) {
stack.push(start);
stack.push(pivot - 1);
}
// 加入右侧新的s与e
if (pivot < end - 1) {
stack.push(pivot + 1);
stack.push(end);
}
while (!stack.isEmpty()) {
end = stack.pop();
start = stack.pop();
pivot = partition(array,start,end);
// 加入左侧新的s与e
if (pivot > start + 1) {
stack.push(start);
stack.push(pivot - 1);
}
// 加入右侧新的s与e
if (pivot < end - 1) {
stack.push(pivot + 1);
stack.push(end);
}
}
}
private int partition(int[] array, int left, int right) {
int tmp = array[left];
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
while (left < right && array[left] < tmp) {
left++;
}
array[right] = array[left];
}
// 最后将基准值放到 left 与 right 相遇处
array[left] = tmp;
return right;
}(3) 测试图
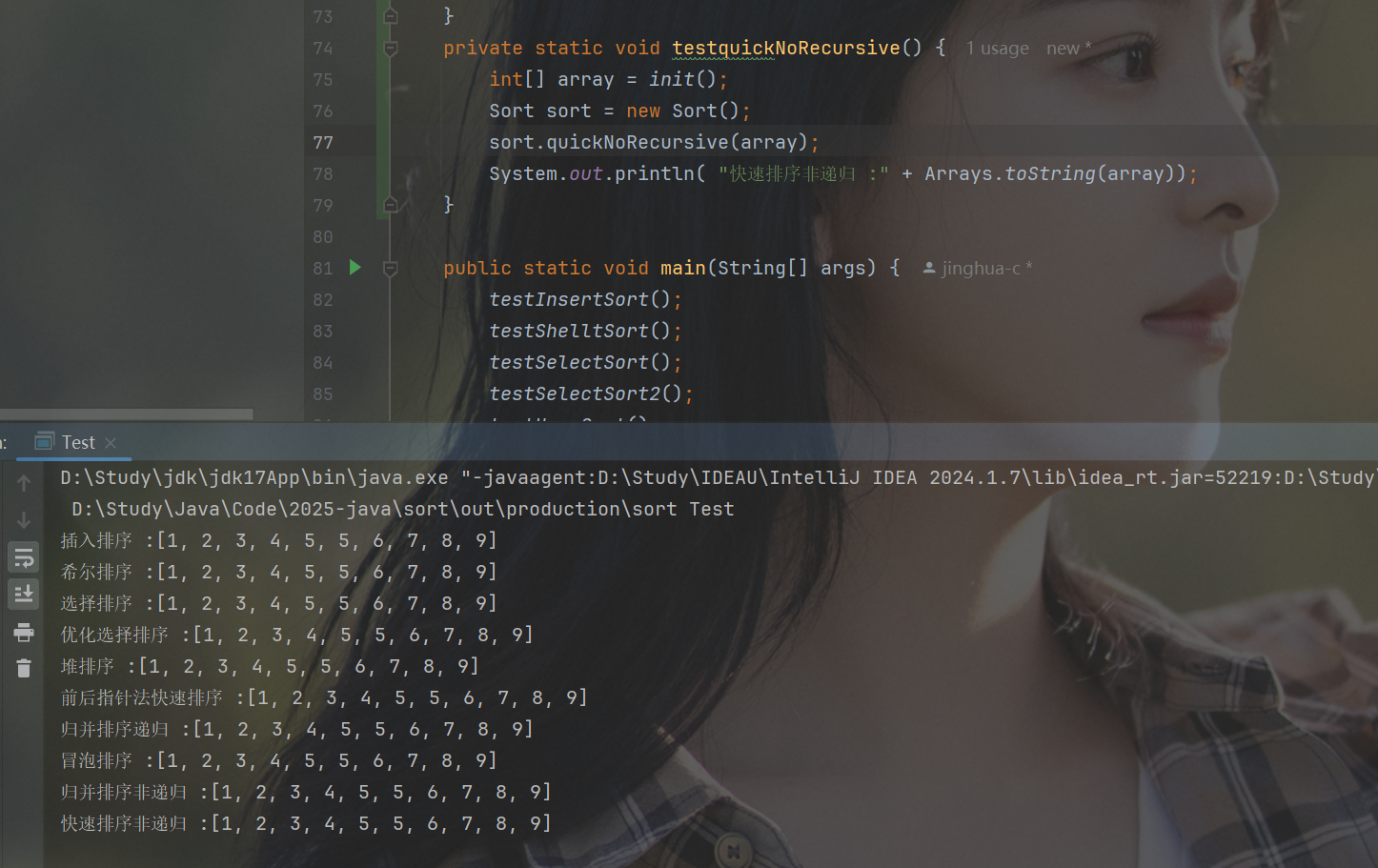
在这里插入图片描述
4. 复杂度
1.时间复杂度: O(N*logN) 2.空间复杂度: O(logN) 3.稳定性: 不稳定
5. 优化
1.快速排有很多优化方式,比如在获取基准值时, 我们不直接将left下标的值设置为基准,而是采用三数取中的方式先大致确定一个基准值, 然后将这个取得中间值与left下标值交换, 这种就可以避免一些极端情况(顺序或逆序)导致的时间与空间复杂度剧增, 优化的代码如下
public void quickSort(int[] array) {
quick(array,0,array.length - 1);
}
private void quick(int[] array, int left, int right) {
if (left >= right) {
return;
}
// 获取pivot值
threeToMid(array, left, right);
int pivot = partition(array,left,right);
// 递归左
quick(array,left,pivot - 1);
// 递归右
quick(array,pivot + 1,right);
}
private void threeToMid(int[] array, int left, int right) {
int mid = (left + right) / 2;
if (array[left] < array[right]) {
if (array[mid] > array[right]) {
swap(array,left, right);
}else if (array[mid] < array[right] && array[mid] > array[left]){
swap(array,left,mid);
}
}else {
if (array[mid] > array[right] && array[mid] < array[left]) {
swap(array, left, mid);
}else if (array[mid] < array[right]) {
swap(array, left, right);
}
}
}
private int partition(int[] array, int left, int right) {
int tmp = array[left];
while (left < right) {
while (left < right && array[right] >= tmp) {
right--;
}
array[left] = array[right];
while (left < right && array[left] < tmp) {
left++;
}
array[right] = array[left];
}
// 最后将基准值放到 left 与 right 相遇处
array[left] = tmp;
return right;
}2.当遇到数组递归到较小区间的时候,这时候数组已经是趋于有序的这种情况了, 那么我们可以在这里使用直接插入排序, 来实现快速达到有序 3.快排还有许多种优化方式, 这里就不一一列举, 感兴趣的兄弟可以去深入探索…

在这里插入图片描述
七. 归并排序
1. 递归算法
(1) 算法原理
归并排序也是一种稳定的排序, 这个排序是一个严格意义上的从中间等分, 该排序在面试中也十分常见与常考, 下面是图解, 对归并排序相关题目感兴趣的可以去算法奇妙屋(四)-归并分治这篇博客看一下相关题目解法
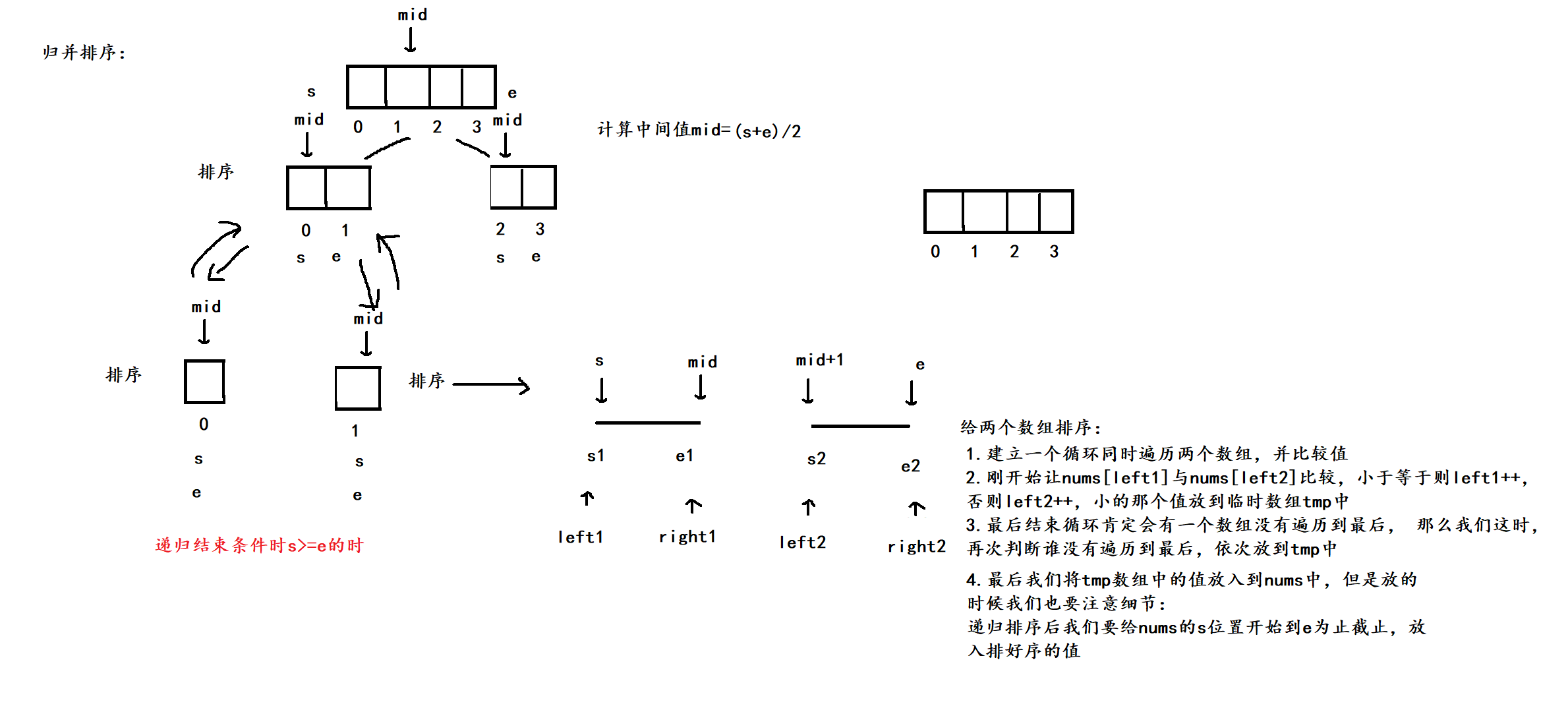
在这里插入图片描述
(2) 代码
public void mergeSort(int[] array) {
mergeChild(array, 0, array.length - 1);
}
private void mergeChild(int[] array, int start, int end) {
if (start >= end) {
return;
}
int mid = (start + end) / 2;
// 分解左边数组
mergeChild(array, start, mid);
// 分解右边数组
mergeChild(array, mid + 1, end);
// 合并数组
merge(array,start,mid,end);
}
private void merge(int[] array, int start, int mid, int end) {
int left1 = start;
int left2 = mid + 1;
int i = 0;
int[] tmp = new int[end - start + 1];
while (left1 <= mid && left2 <= end) {
if (array[left1] <= array[left2]) {
tmp[i++] = array[left1++];
}else {
tmp[i++] = array[left2++];
}
}
while (left1 <= mid) {
tmp[i++] = array[left1++];
}
while (left2 <= end) {
tmp[i++] = array[left2++];
}
for (int j = 0; j < end - start + 1; j++) {
array[start + j] = tmp[j];
}
}(3) 测试图
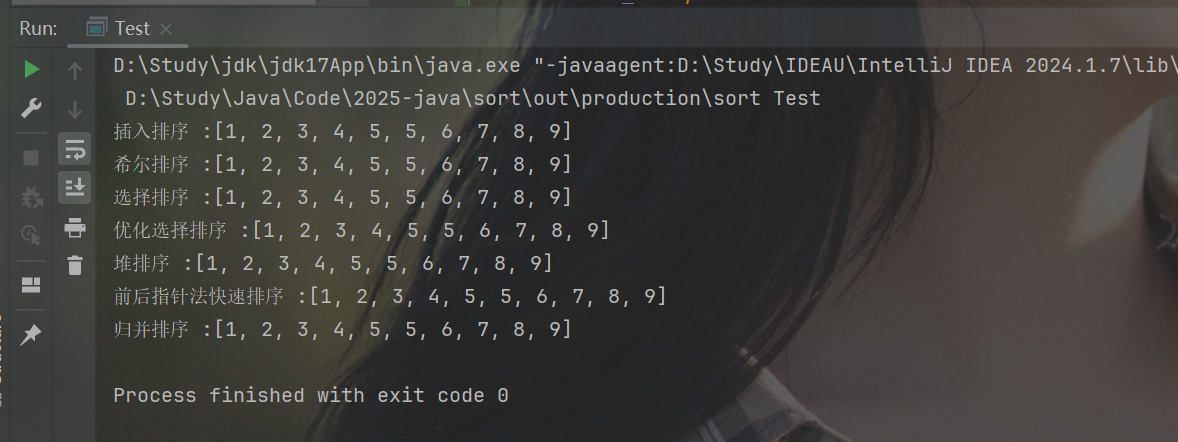
在这里插入图片描述
2. 非递归算法
(1) 算法原理
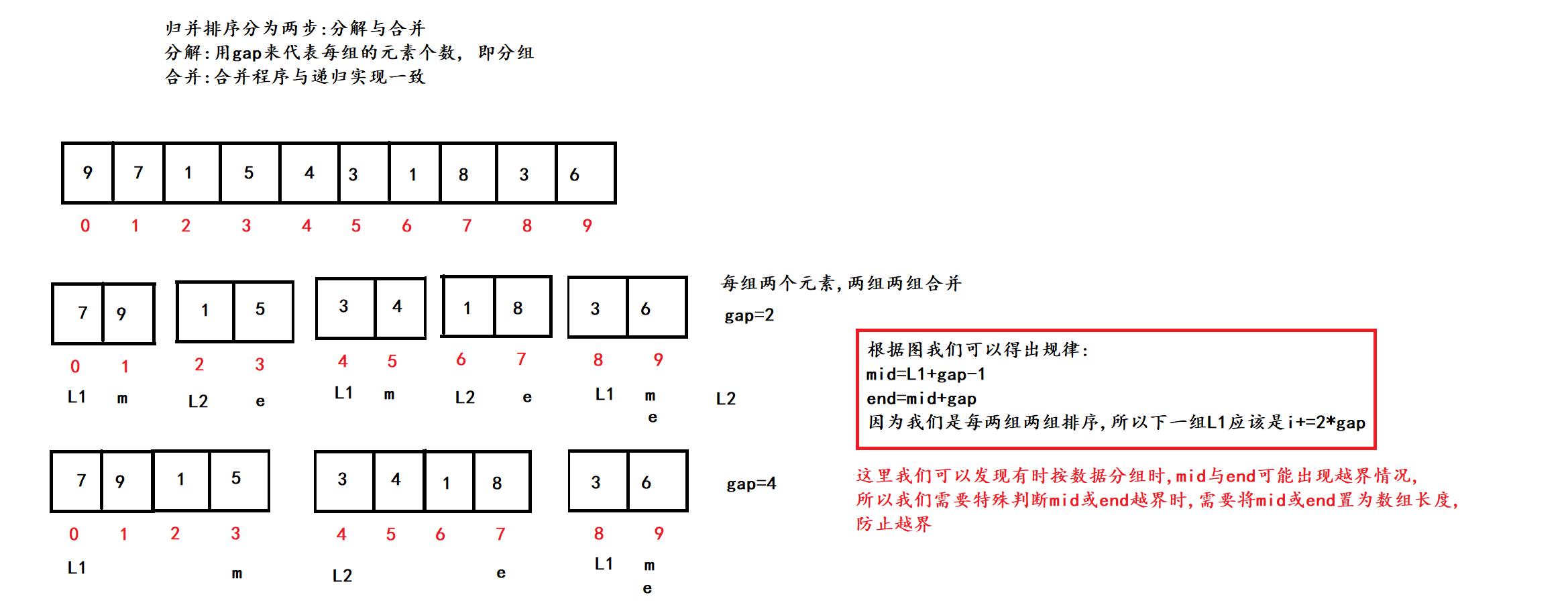
在这里插入图片描述
(2) 代码
public void mergeNoRecursive(int[] array) {
int gap = 1;
while (gap < array.length) {
for (int i = 0; i < array.length; i += 2 * gap) {
int start = i;
int mid = start + gap - 1;
if (mid >= array.length) {
mid = array.length - 1;
}
int end = mid + gap;
if (end >= array.length) {
end = array.length - 1;
}
merge(array,start,mid,end);
}
gap *= 2;
}
}
private void merge(int[] array, int start, int mid, int end) {
int left1 = start;
int left2 = mid + 1;
int i = 0;
int[] tmp = new int[end - start + 1];
while (left1 <= mid && left2 <= end) {
if (array[left1] <= array[left2]) {
tmp[i++] = array[left1++];
}else {
tmp[i++] = array[left2++];
}
}
while (left1 <= mid) {
tmp[i++] = array[left1++];
}
while (left2 <= end) {
tmp[i++] = array[left2++];
}
for (int j = 0; j < end - start + 1; j++) {
array[start + j] = tmp[j];
}
}(3) 测试图
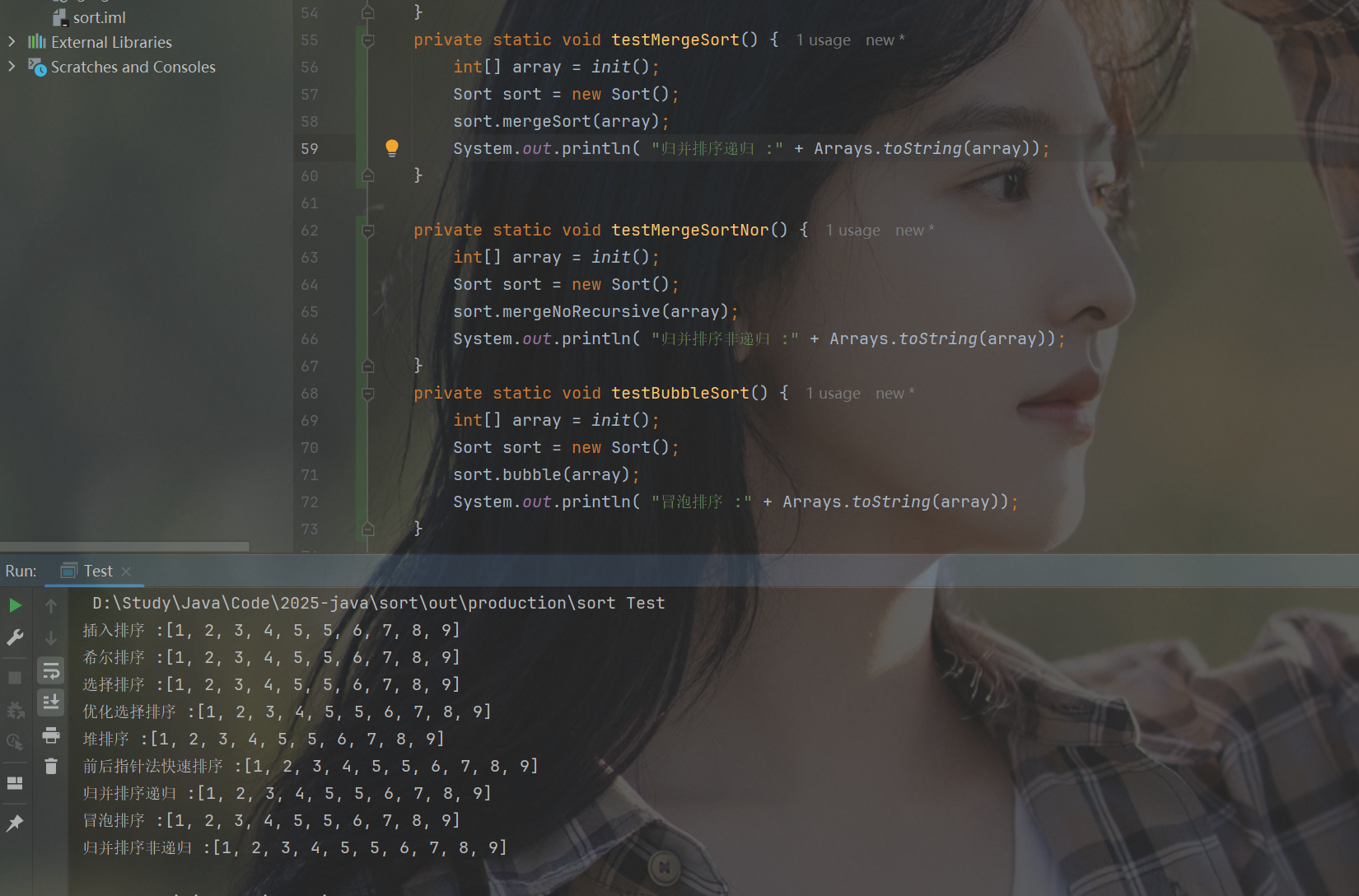
在这里插入图片描述
4. 复杂度
1.时间复杂度: O(N*logN) 2.空间复杂度: O(N) 3.稳定性: 稳定

在这里插入图片描述
八. 冒泡排序
1. 算法原理
该排序可以说是最常见的排序, 记得当初博主第一个学的就是这个排序, 花了好长时间才搞明白, 下面我们直接上图
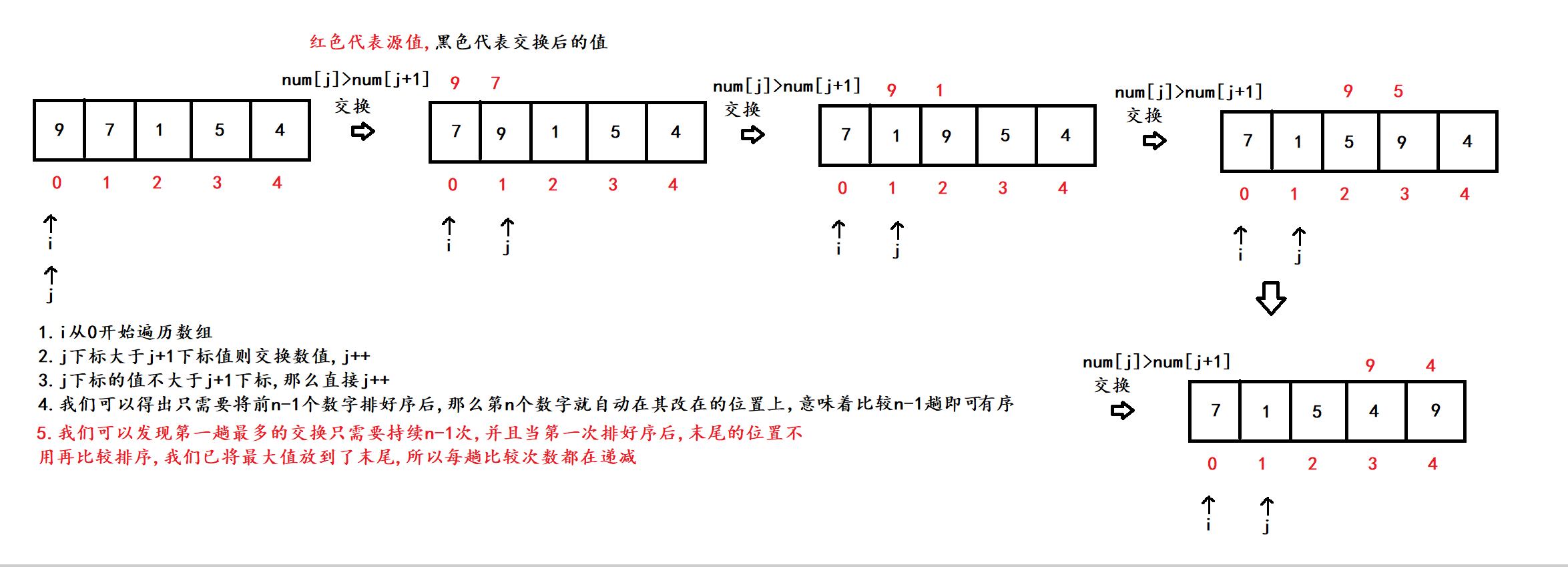
在这里插入图片描述
2. 代码
private void swap(int[] array, int i, int index) {
int tmp = array[i];
array[i] = array[index];
array[index] = tmp;
}
public void bubble(int[] num) {
for (int i = 0; i < num.length - 1; i++) {
for (int j = 0; j < num.length - 1 - i; j++) {
if (num[j] > num[j + 1]) {
swap(num, j, j + 1);
}
}
}
}3. 测试

4. 复杂度
1.时间复杂度: O(N^2)
2.空间复杂度: O(1)
3.稳定性: 稳定
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-12-08,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

