链表进化论:C语言实现带哨兵位的双向循环链表,解锁O(1)删除的奥秘
链表进化论:C语言实现带哨兵位的双向循环链表,解锁O(1)删除的奥秘

Extreme35
发布于 2025-12-23 18:27:30
发布于 2025-12-23 18:27:30

在这里插入图片描述
🏠 个人主页: EXtreme35
📚 个人专栏:
专栏名称 | 专栏主题简述 |
|---|---|
《C语言》 | C语言基础、语法解析与实战应用 |
《数据结构》 | 线性表、树、图等核心数据结构详解 |
《题解思维》 | 算法思路、解题技巧与高效编程实践 |

在这里插入图片描述
1. 链表家族的八大结构:分类与选择
在数据结构领域,链表是一种灵活多变的结构。通过组合不同的连接方式和头部处理策略,我们可以衍生出八种主要的链表形态。了解这些分类,有助于我们理解本次实现的双向循环带哨兵位链表为何是最强大、最灵活的形态之一。
链表的八种基本分类: 链表结构由两个核心维度组合而成:基础结构(4种)和头部处理方式(2种),共
种形态。
序号 | 基础结构 | 首尾关系 | 头部处理 | 核心特性与优势 |
|---|---|---|---|---|
1 | 单向非循环 | 尾 → \rightarrow → NULL | 不带头结点 | 最基础,内存开销最小。 |
2 | 单向非循环 | 尾 → \rightarrow → NULL | 带头结点 | 统一头插/头删操作,简化代码边界处理。 |
3 | 单向循环 | 尾 → \rightarrow → 头 | 不带头结点 | 适用于环形任务调度、遍历无需判空。 |
4 | 单向循环 | 尾 → \rightarrow → 头 | 带头结点 | 结合了循环和头结点的优势。 |
5 | 双向非循环 | 尾 → \rightarrow → NULL | 不带头结点 | 双向遍历,已知节点 O ( 1 ) O(1) O(1) 删除。 |
6 | 双向非循环 | 尾 → \rightarrow → NULL | 带头结点 | 统一双向操作的入口。 |
7 | 双向循环 | 尾 → \rightarrow → 头 | 不带头结点 | 复杂的双向环形结构。 |
8 | 双向循环 | 尾 → \rightarrow → 头 | 带头结点 | 最完善。所有 O ( 1 ) O(1) O(1) 插入/删除操作逻辑高度统一。 |
NULL不带头结点最基础,内存开销最小。2单向非循环尾
NULL带头结点统一头插/头删操作,简化代码边界处理。3单向循环尾
头不带头结点适用于环形任务调度、遍历无需判空。4单向循环尾
头带头结点结合了循环和头结点的优势。5双向非循环尾
NULL不带头结点双向遍历,已知节点
删除。6双向非循环尾
NULL带头结点统一双向操作的入口。7双向循环尾
头不带头结点复杂的双向环形结构。8双向循环尾
头带头结点最完善。所有
插入/删除操作逻辑高度统一。
我们本次实现和讨论的,正是结构最复杂、但在实际工程应用中操作效率最高、代码最简洁的 第八种 结构。
2. 单链表的局限与双链表的呼唤
在数据结构的世界里,单向链表是我们最早接触到的动态存储结构之一。它通过一个指针域 next,将零散的内存空间串联起来,实现了灵活的数据组织。然而,随着我们对数据操作复杂度的要求提升,单链表的几大局限性也逐渐凸显:
- 单向遍历,缺乏灵活性: 节点只能从前向后访问。一旦需要反向查找或从尾部高效操作,就不得不从头开始遍历,操作效率低下。
- 删除操作的痛点: 在单链表中删除一个已知节点
时,我们无法直接通过
访问其前驱节点
。这意味着,我们必须从链表头部开始遍历,直到找到
,才能完成
的断链操作。这无疑增加了时间开销。
- 特定场景效率低: 对于需要频繁进行“插入到前驱”或“获取前驱”的操作场景,单链表表现不佳。
正是基于这些限制,一种更加强大、灵活的链式结构应运而生——双向链表(Doubly Linked List)。它在空间上做出了一点小小的“牺牲”,却换来了时间效率上的巨大飞跃。下面,我们就深入解析这一高效的数据结构。
3. 双链表核心概念解析:双指针,效率翻倍
双向链表的设计核心在于其节点结构的升级,使得数据项的访问不再受限于单一方向。
核心节点结构
双链表的节点结构相比单链表多了一个关键指针:prev。
data: 存储实际数据,类型为LTDataType(在此实现中是int)。next: 指向下一个节点的指针(与单链表相同)。prev: 指向前一个节点的指针(双链表的关键)。
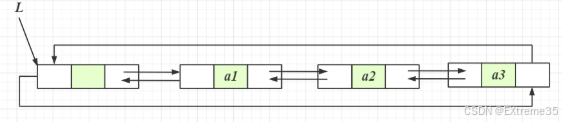
在这里插入图片描述
typedef int LTDataType;
typedef struct ListNode
{
LTDataType data;
struct ListNode* next; // 指向下一个节点
struct ListNode* prev; // 指向前一个节点
}LTNode;核心特性:双向遍历与本质区别
由于每个节点同时持有前后两个节点的地址,双向链表具备以下核心特性:
- 双向遍历特性:
- 可以通过
pcur = pcur->next从前往后遍历。 - 也可以通过
pcur = pcur->prev从后往前遍历。
- 可以通过
- 本质区别:操作效率的提升
- 插入操作: 在
N 之后插入一个新节点,需要调整
N 的
next和N \rightarrow next 的
prev。- 删除操作: 要删除节点
N ,直接通过
N \rightarrow prev 找到前驱,通过
N \rightarrow next 找到后继。然后执行:
N \rightarrow prev \rightarrow next = N \rightarrow next N \rightarrow next \rightarrow prev = N \rightarrow prev
这个过程是
时间复杂度的,无需像单链表那样进行
的查找操作! 这彻底解决了单链表无法反向访问的痛点,核心优势在于对已知节点
的操作。
特殊的结构:带哨兵位循环链表
我们本次实现采用了最高效、最简洁的设计:带哨兵位的循环双向链表。
- 哨兵位(
phead): 一个不存储有效数据、永远存在的特殊头结点。 - 循环特性: 链表的最后一个节点的
next指向哨兵位 (phead),哨兵位的prev指向最后一个节点。
这种设计的好处是:所有对数据的操作(头插、尾插、头删、尾删、中间插入/删除)都可以被统一处理,无需特殊判断链表为空的情况!
4. 操作实现与思路解析
1. 节点管理与初始化
1.1 申请节点 (LTBuyNode)
实现思路:
- 使用
malloc动态分配一个LTNode大小的内存空间。 - 检查分配是否成功,失败则报错退出。
- 将传入的数据
x赋给节点的data域。 - 关键: 由于这是一个双向循环链表,初始化的节点应将其
next和prev指针都指向自身,以保证节点的独立性和通用性。
代码实现:
//申请节点
LTNode* LTBuyNode(LTDataType x)
{
LTNode* node = (LTNode*)malloc(sizeof(LTNode));
if (node == NULL)
{
perror("malloc fail!");
exit(1);
}
node->data = x;
// 初始时,节点的next和prev都指向自身
node->next = node->prev = node;
return node;
}1.2 初始化
实现思路:
- 创建一个哨兵位(头结点)。哨兵位不存储有效数据,只是作为链表的起点/终点标记。
- 直接调用
LTBuyNode创建一个节点,并将其作为链表的头结点返回。此时,这个哨兵位节点通过LTBuyNode的初始化,其next和prev均指向自身,代表一个空的双向循环链表。
代码实现:
//初始化
LTNode* LTInit()
{
LTNode* phead = LTBuyNode(-1); // -1 仅用于标记,实际数据无意义
return phead;
}2. 插入操作
所有的插入操作都是
的时间复杂度,其核心在于调整四个指针,将新节点 newnode 插入到 pos 和 pos->next 之间。
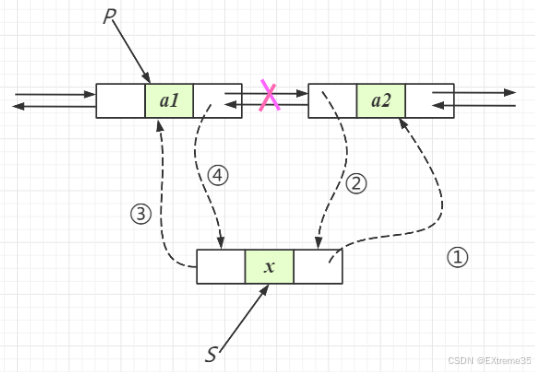
在这里插入图片描述
2.1 尾插
实现思路: 尾插等效于在哨兵位头结点 phead 的前面插入节点。
- 创建新节点
newnode。 - 确定插入位置:在
phead->prev(原尾节点)和phead(哨兵位)之间。 - 四指针调整:
newnode->prev = phead->prev(新节点指向原尾节点)newnode->next = phead(新节点指向哨兵位)phead->prev->next = newnode(原尾节点的next指向新节点)phead->prev = newnode(哨兵位的prev指向新节点)
代码实现:
//尾插
void LTPushBack(LTNode* phead, LTDataType x)
{
assert(phead);
LTNode* newnode = LTBuyNode(x);
// phead <-> phead->prev <-> newnode <-> phead
newnode->prev = phead->prev;
newnode->next = phead;
phead->prev->next = newnode;
phead->prev = newnode;
}2.2 头插
实现思路: 头插等效于在哨兵位头结点 phead 的后面插入节点。
- 创建新节点
newnode。 - 确定插入位置:在
phead(哨兵位)和phead->next(原头节点)之间。 - 四指针调整:
newnode->next = phead->next(新节点指向原头节点)newnode->prev = phead(新节点指向哨兵位)phead->next->prev = newnode(原头节点的prev指向新节点)phead->next = newnode(哨兵位的next指向新节点)
代码实现:
//头插
void LTPushFront(LTNode* phead, LTDataType x)
{
assert(phead);
LTNode* newnode = LTBuyNode(x);
// phead <-> newnode <-> phead->next
newnode->next = phead->next;
newnode->prev = phead;
phead->next->prev = newnode;
phead->next = newnode;
}2.3 指定位置插入
实现思路: 在给定的位置 pos 之后插入节点,这是插入操作的通用模板。
- 创建新节点
newnode。 - 确定插入位置:在
pos和pos->next之间。 - 四指针调整:
newnode->next = pos->next(新节点指向pos的后继)newnode->prev = pos(新节点指向pos)pos->next->prev = newnode(pos后继的prev指向新节点)pos->next = newnode(pos的next指向新节点)
代码实现:
//在pos位置之后插入数据
void LTInsert(LTNode* pos, LTDataType x)
{
assert(pos);
LTNode* newnode = LTBuyNode(x);
// pos <-> newnode <-> pos->next
newnode->next = pos->next;
newnode->prev = pos;
pos->next->prev = newnode;
pos->next = newnode;
}3. 删除操作
所有的删除操作都是
的时间复杂度,其核心在于调整两个指针的 next 和 prev,然后释放被删除节点的内存。
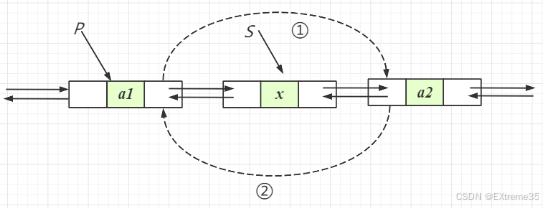
在这里插入图片描述
3.1 尾删
实现思路: 删除链表中有效数据的最后一个节点(即 phead->prev)。
- 校验: 链表必须不为空(即
phead->next != phead)。 - 定位要删除的节点
del = phead->prev。 - 两指针调整: 让
del的前驱直接连接到phead。del->prev->next = phead(原倒数第二个节点的next指向哨兵位)phead->prev = del->prev(哨兵位的prev指向原倒数第二个节点)
- 释放
del节点的内存。
代码实现:
//尾删
void LTPopBack(LTNode* phead)
{
// 链表必须有效且链表不能为空(只有一个哨兵位)
assert(phead && phead->next != phead);
LTNode* del = phead->prev; // del即为尾节点
// phead <-> del->prev <-> del
del->prev->next = phead;
phead->prev = del->prev;
free(del);
del = NULL;
}3.2 头删
实现思路: 删除链表中有效数据的第一个节点(即 phead->next)。
- 校验: 链表必须不为空。
- 定位要删除的节点
del = phead->next。 - 两指针调整: 让
phead直接连接到del的后继。phead->next = del->next(哨兵位的next指向原第二个节点)del->next->prev = phead(原第二个节点的prev指向哨兵位)
- 释放
del节点的内存。
代码实现:
//头删
void LTPopFront(LTNode* phead)
{
assert(phead && phead->next != phead);
LTNode* del = phead->next; // del即为头节点
// phead <-> del <-> del->next
phead->next = del->next;
del->next->prev = phead;
free(del);
del = NULL;
}3.3 删除指定节点
实现思路: 删除已知的节点 pos。这是删除操作的通用模板。
- 校验:
pos必须有效(且在逻辑上不能是哨兵位)。 - 两指针调整: 让
pos的前驱直接连接到pos的后继。pos->next->prev = pos->prev(后继节点的prev指向pos的前驱)pos->prev->next = pos->next(前驱节点的next指向pos的后继)
- 释放
pos节点的内存。
代码实现:
//删除pos节点
void LTErase(LTNode* pos)
{
assert(pos);
// pos->prev <-> pos <-> pos->next
pos->next->prev = pos->prev;
pos->prev->next = pos->next;
free(pos);
pos = NULL;
}4. 查找与遍历
4.1 查找
实现思路: 查找操作仍需遍历。从哨兵位 phead 的下一个节点(即第一个有效数据节点)开始,沿着 next 指针遍历,直到回到 phead。在遍历过程中,比对节点的 data 是否等于目标值 x。
- 初始化指针
pcur = phead->next。 - 循环条件:
pcur != phead(遍历到哨兵位即停止)。 - 如果找到匹配数据,立即返回
pcur。 - 若遍历结束未找到,返回
NULL。
代码实现:
LTNode* LTFind(LTNode* phead, LTDataType x)
{
LTNode* pcur = phead->next;
while (pcur != phead)
{
if (pcur->data == x)
return pcur;
pcur = pcur->next;
}
// 没有找到
return NULL;
}4.2 打印
实现思路: 遍历链表,打印所有有效数据。与查找类似,从 phead->next 开始,沿着 next 指针移动,直到回到 phead。
代码实现:
void LTPrint(LTNode* phead)
{
LTNode* pcur = phead->next;
while (pcur != phead)
{
printf("%d->", pcur->data);
pcur = pcur->next;
}
printf("head(loop)\n"); // 打印结束标记
}4.3 销毁
实现思路: 销毁操作需要释放链表中的所有节点内存,包括哨兵位 phead。
- 从第一个有效节点
phead->next开始遍历。 - 在释放当前节点前,必须先用一个临时指针(
next)保存下一个节点的地址,防止“野指针”问题。 - 释放当前节点。
- 移动到下一个节点,直到
pcur重新指向phead。 - 最后释放哨兵位
phead。
代码实现:
void LTDesTroy(LTNode* phead)
{
assert(phead);
LTNode* pcur = phead->next;
while (pcur != phead)
{
LTNode* next = pcur->next; // 提前保存下一个节点的地址
free(pcur);
pcur = next;
}
// 此时pcur指向phead,最后销毁哨兵位
free(phead);
phead = NULL;
}5. 性能提升一览
双链表最大的优势在于其对插入和删除操作的优化。下表对比了单链表和双链表在常见操作上的渐进时间复杂度。
操作类型 | 单链表 | 双向链表(带哨兵) | 备注 |
|---|---|---|---|
初始化 | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) | 均创建头节点 |
头插/头删 | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) | 均高效 |
尾插/尾删 | O ( N ) O(N) O(N) | O ( 1 ) O(1) O(1) | 双链表可直接访问尾节点的前驱,实现 O ( 1 ) O(1) O(1) |
按值查找 | O ( N ) O(N) O(N) | O ( N ) O(N) O(N) | 均需遍历 |
已知节点 N N N 后的插入 | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) | |
已知节点 N N N 的删除 | O ( N ) O(N) O(N) | O ( 1 ) O(1) O(1) | 双链表可通过 N->prev 直接找到前驱 |
空间复杂度 | O ( N ) O(N) O(N) | O ( N ) O(N) O(N) | 双链表额外存储 prev 指针,常数因子更大 |
均创建头节点头插/头删
均高效尾插/尾删
双链表可直接访问尾节点的前驱,实现
按值查找
均需遍历已知节点
后的插入
已知节点
的删除
双链表可通过 N->prev 直接找到前驱空间复杂度
双链表额外存储 prev 指针,常数因子更大
从表格中可以清晰看出,双向链表在尾部操作和已知节点删除方面拥有绝对的性能优势,将复杂度从
优化到了
。
6. 实际应用场景
双向链表因其双向访问和高效删除的特性,在多个核心领域得到广泛应用:
- 实现 LRU 缓存淘汰算法: LRU (Least Recently Used) 算法需要频繁将最近访问的元素移动到链表头部,并将链表尾部的旧元素淘汰。双链表可以实现
的头部插入和尾部删除,是实现 LRU 的首选结构。
- 浏览器历史记录与编辑器撤销/重做: “前进”和“后退”(浏览历史)或“撤销”和“重做”(文本编辑)功能本质上就是对数据序列进行双向操作。双链表可以轻松实现双向导航和快速插入新的操作记录。
- 高级数据结构的底层实现:
例如,许多语言中的
Deque(双端队列)底层就是用双链表来实现的,以保证在两端的操作都达到
的时间复杂度。
7. 总结
双向循环链表(带哨兵位)是 C 语言数据结构中的一个优雅且高效的设计。
它通过在节点中引入 prev 指针,彻底解决了单链表在反向遍历和高效删除方面的痛点,将尾部操作和已知节点删除的复杂度从
优化到令人满意的
。而哨兵位和循环的结合,进一步简化了代码逻辑,消除了大量边界条件的判断。
掌握双链表的实现,是能够设计和实现高效算法的关键一步!
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-12-03,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

