深入理解 C 语言中的二分法查找：从代码解析到实践优化

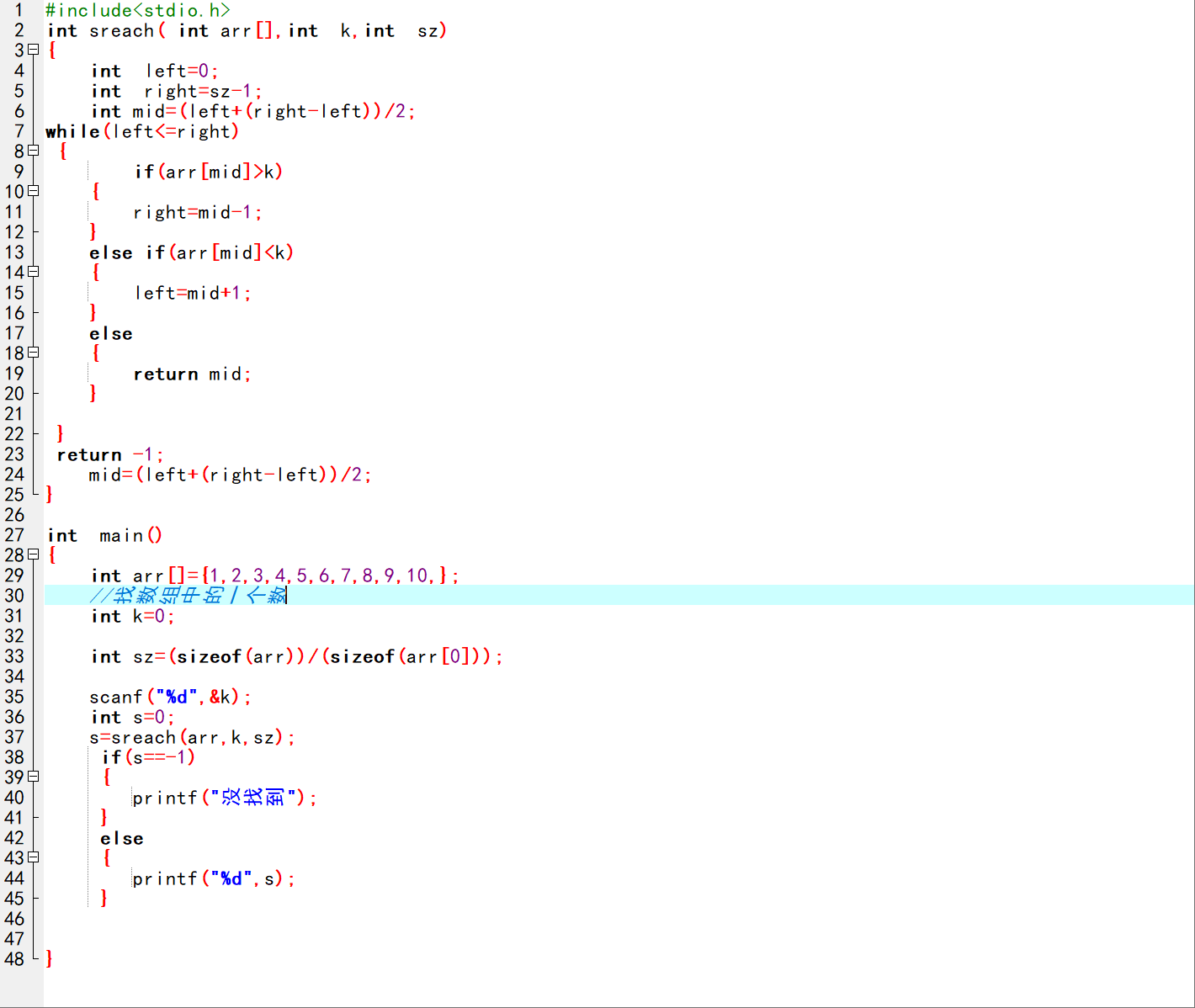
在 C 语言的数据查找领域，二分法查找凭借其高效的性能，成为处理有序数组查找问题的 “利器”。它与顺序查找逐元素遍历的方式不同，通过不断将查找范围减半，能大幅减少比较次数，尤其在数据量较大时，优势更为明显。今天，我们就以一段具体的 C 语言代码为切入点，带大家全面认识二分法查找的实现逻辑、代码细节以及优化方向。

一、二分法查找的核心原理

在正式分析代码前，我们先明确二分法查找的适用条件和核心逻辑。二分法查找仅适用于有序数组（本文以升序数组为例），其核心思路可概括为 “三步走”：

1. 确定查找范围的左右边界（初始时左边界为数组起始索引0，右边界为数组最后一个元素的索引sz-1，其中sz为数组长度）；
2. 计算查找范围的中间索引mid，并比较中间元素arr[mid]与目标值k；
3. 根据比较结果调整查找范围：

• • 若arr[mid] > k：说明目标值在左半部分，将右边界更新为mid-1；
• • 若arr[mid] < k：说明目标值在右半部分，将左边界更新为mid+1；
• • 若arr[mid] == k：找到目标值，返回中间索引mid。

若循环结束后仍未找到目标值（即左边界大于右边界），则返回-1表示查找失败。

二、代码逐段解析：二分法的 C 语言实现

接下来，我们结合你提供的代码，逐部分拆解二分法查找的实现过程，同时梳理代码中的关键细节与潜在问题。

1. 头文件与函数声明

#include<stdio.h>

int sreach(int arr[], int k, int sz);

• #include<stdio.h>：引入标准输入输出头文件，为后续的scanf（输入目标值）和printf（输出结果）函数提供支持；
• int sreach(int arr[], int k, int sz)：声明二分法查找函数 sreach（注：标准拼写应为search，此处为代码笔误），函数参数含义如下：
• • int arr[]：传入待查找的有序数组（在函数中，数组名会退化为指针，指向数组首元素）；
• • int k：传入需要查找的目标值；
• • int sz：传入数组的长度（数组长度需在主函数中计算，因为函数内部无法通过sizeof(arr)获取真实数组长度）。

2. 二分法查找函数实现（核心部分）

int sreach(int arr[], int k, int sz)

{

int left = 0; // 左边界初始化为数组起始索引

int right = sz - 1; // 右边界初始化为数组末尾索引

int mid = (left + (right - left)) / 2; // 计算中间索引

while (left <= right) // 循环条件：左边界 <= 右边界（表示查找范围有效）

{

if (arr[mid] > k)

{

right = mid - 1; // 目标值在左半部分，更新右边界

}

else if (arr[mid] < k)

{

left = mid + 1; // 目标值在右半部分，更新左边界

}

else

{

return mid; // 找到目标值，返回索引

}

}

return -1; // 循环结束未找到，返回-1表示失败

mid = (left + (right - left)) / 2; // 无效代码：执行不到此处

}

（1）关键变量初始化

• left = 0和right = sz - 1：明确初始查找范围为整个数组，这是二分法的基础；
• mid = (left + (right - left)) / 2：计算中间索引的 “安全写法”。这里需要注意，若直接使用(left + right) / 2，当left和right均为较大整数时，可能会出现 “整数溢出” 问题（例如left=2^30、right=2^30，left+right会超过int类型的最大值），而(left + (right - left)) / 2等价于(left + right) / 2，却能有效避免溢出，是工业级代码中常用的写法。

（2）循环逻辑与查找过程

循环条件left <= right是二分法的核心细节之一：

• 当left == right时，查找范围缩小到单个元素，此时仍需判断该元素是否为目标值，因此循环条件不能写成left < right（否则会漏掉最后一个元素的判断）；
• 每次循环中，根据arr[mid]与k的大小关系调整left或right，本质是将查找范围 “减半”，这也是二分法时间复杂度为O(log n)（n为数组长度）的原因 —— 例如，查找长度为 1000 的数组，最多只需 10 次循环（2^10=1024）。

（3）代码中的潜在问题

细心的同学会发现，函数末尾有一行mid = (left + (right - left)) / 2，但这行代码在return -1之后，永远无法被执行，属于 “无效代码”，在实际编程中需要删除，避免冗余。

3. 主函数：数据准备与函数调用

主函数的作用是准备待查找的有序数组、获取用户输入的目标值、调用二分法函数并输出结果，是整个程序的 “入口” 和 “控制中心”。

int main()

{

int arr[] = {1,2,3,4,5,6,7,8,9,10,}; // 待查找的有序数组（升序）

int k = 0; // 目标值初始化

int sz = (sizeof(arr)) / (sizeof(arr[0])); // 计算数组长度

scanf("%d", &k); // 获取用户输入的目标值k

int s = 0;

s = sreach(arr, k, sz); // 调用二分法查找函数，接收返回结果

if (s == -1)

{

printf("没找到"); // 查找失败：输出提示

}

else

{

printf("%d", s); // 查找成功：输出目标值的索引

}

return 0; // 主函数正常结束

}

（1）数组长度计算

sz = (sizeof(arr)) / (sizeof(arr[0]))是 C 语言中计算数组长度的标准写法：

• sizeof(arr)：计算整个数组所占的字节数（例如arr为 10 个int元素的数组，若int为 4 字节，则sizeof(arr)=40）；
• sizeof(arr[0])：计算数组单个元素所占的字节数（此处为 4 字节）；
• 两者相除得到数组的元素个数（即长度sz=10）。

需要注意的是，数组长度必须在主函数中计算，不能在 sreach函数中计算 —— 因为在函数参数中，arr[]会退化为指针，sizeof(arr)得到的是指针的字节数（例如 32 位系统中为 4 字节），而非数组的真实长度，若在函数中计算会导致结果错误。

（2）用户交互与结果输出

• scanf("%d", &k)：获取用户从键盘输入的目标值k，例如用户输入 “5”，则k=5；
• 调用 sreach(arr, k, sz)后，将返回的索引值赋给变量s：
• • 若s=-1：说明未找到目标值，输出 “没找到”；
• • 若s为非负整数：说明找到目标值，输出其在数组中的索引（例如k=5时，返回索引4，输出 “4”）。

三、代码优化与测试：让二分法更严谨

为了让代码更规范、更健壮，我们针对上述问题进行优化，并通过测试案例验证二分法的正确性。

1. 代码优化点

• 修正函数名拼写：将sreach改为标准拼写search，提升代码可读性；
• 删除无效代码：移除函数末尾无法执行的mid重新赋值语句；
• 增加代码注释：在关键步骤添加注释，方便他人理解（尤其是团队协作场景）；
• 优化输出信息：查找成功时，不仅输出索引，还可输出目标值，让结果更直观（例如 “找到目标值 5，索引为 4”）。

优化后的完整代码如下：

#include<stdio.h>

// 二分法查找函数声明：在有序数组arr中查找目标值k，返回索引（失败返回-1）

int search(int arr[], int k, int sz);

int search(int arr[], int k, int sz)

{

int left = 0; // 左边界：数组起始索引

int right = sz - 1; // 右边界：数组末尾索引

while (left <= right) // 查找范围有效（左<=右）

{

// 计算中间索引，避免left+right溢出

int mid = left + (right - left) / 2;

if (arr[mid] > k)

{

right = mid - 1; // 目标值在左半部分，缩小右边界

}

else if (arr[mid] < k)

{

left = mid + 1; // 目标值在右半部分，扩大左边界

}

else

{

return mid; // 找到目标值，返回索引

}

}

return -1; // 查找失败，返回-1

}

int main()

{

int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; // 升序有序数组

int k = 0; // 目标值

// 计算数组长度：总字节数 / 单个元素字节数

int sz = sizeof(arr) / sizeof(arr[0]);

printf("请输入要查找的目标值：");

scanf("%d", &k);

// 调用二分法查找函数

int result = search(arr, k, sz);

// 输出查找结果

if (result == -1)

{

printf("没找到目标值%d\n", k);

}

else

{

printf("找到目标值%d，其在数组中的索引为%d\n", k, result);

}

return 0;

}

2. 测试案例验证

我们通过 3 组典型测试案例，验证优化后代码的正确性：

• 案例 1：目标值在数组中间（如k=5）：

输入5，输出 “找到目标值 5，其在数组中的索引为 4”，符合预期（数组索引从 0 开始，第 5 个元素索引为 4）；

• 案例 2：目标值在数组边界（如k=1或k=10）：

输入1，输出 “找到目标值 1，其在数组中的索引为 0”；输入10，输出 “找到目标值 10，其在数组中的索引为 9”，边界情况处理正确；

• 案例 3：目标值不在数组中（如k=11或k=0）：

输入11，输出 “没找到目标值 11”；输入0，输出 “没找到目标值 0”，查找失败处理正确。

四、二分法的适用场景与局限性

通过以上分析，我们不仅掌握了二分法的 C 语言实现，还需要明确它的适用场景与局限性，以便在实际开发中合理选择查找算法：

• 适用场景：

1. 1. 处理有序数组（升序或降序，降序只需调整比较逻辑）；
2. 1. 数据量较大且查找频繁的场景（二分法的O(log n)时间复杂度远优于顺序查找的O(n)）；
3. 1. 数组元素不频繁插入 / 删除的场景（若数组频繁变动，需先排序，排序的时间成本可能抵消二分法的优势）。

• 局限性：

1. 1. 不适用于无序数组（若强行使用，需先排序，额外增加时间成本）；
2. 1. 不适用于链表等非连续存储结构（链表无法直接通过索引访问中间元素，需遍历到中间节点，失去二分法的优势）；
3. 1. 若数组中存在多个相同的目标值，二分法只能返回其中一个的索引（如需返回所有相同值的索引，需额外处理）。

五、总结

本文以一段 C 语言代码为载体，从原理、解析、优化到实践，全面讲解了二分法查找的核心逻辑。我们不仅学会了二分法的标准实现（避免整数溢出、正确处理循环条件），还掌握了数组长度计算、函数参数传递等 C 语言基础知识点，同时明确了二分法的适用场景与局限性。

二分法作为一种高效的查找算法，是 C 语言学习中的重要知识点，也是面试中的高频考点。希望通过本文的分析，大家能真正理解二分法的 “减半” 思想，而不仅仅是背诵代码 —— 在后续学习中，还可以尝试基于二分法实现更复杂的功能（如查找有序数组中第一个大于目标值的元素、旋转有序数组的查找等），进一步加深对算法的理解。