信号链中：不相关噪音的重叠计算

继续，讲这个重叠的噪音计算

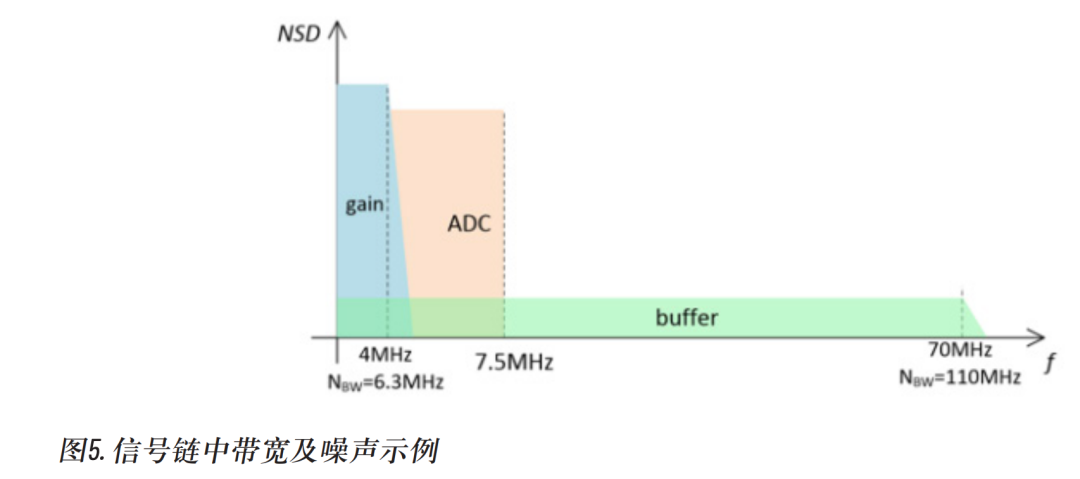
image-20250930094305825

面积代表总噪声：矩形的“高 × 宽”≈ NSD × √NBW，就是 RMS 噪声。哪怕某级 NSD 很低，只要带宽特别宽（如 buffer），总能量仍然大。

各级特征鲜明：

增益级：高密度 + 窄带宽。

缓冲级：低密度 + 宽带宽。

ADC：中等密度 + 中等带宽；这三类噪声叠加后决定整链的噪声地板。

可以看到老生常谈的问题带宽控制极其重要：若缓冲级带宽无限大，它会把很多高频噪声折叠回 Nyquist 内，从而显著抬高系统噪声。

要求增益级尽量低噪声（降低 RTI）；缓冲级带宽要“够用但不多余”（满足采样建立即可）；虽然知道ADC 自身噪声不可避免 → 通过合理增益把信号抬高到满量程，减小 ADC 噪声的相对占比。

图告诉我们：噪声不只看谱密度，还要看带宽；控制缓冲带宽，是降低系统噪声的关键。

噪声叠加的物理规律

在之前我写过几个低噪音测量的文章，其实这个是课本的内容，在一开始的理论部分。

噪声源之间通常是 互不相关（un-correlated） 的随机过程。

对于互不相关噪声，功率相加，幅度不开方相加：

其中 是第 i 个噪声源在频率 f 的谱密度。

最后，积分得到总均方值：

就算这些噪声频率范围重叠，由于它们是随机独立的，不会“互相抵消”，而是功率叠加。

在图 5 里的重叠区

以 4 MHz–7.5 MHz 区间为例：

蓝色（增益级）、橙色（ADC）、绿色（buffer）的谱密度都“同时存在”。

在这段频率里，瞬时的总 NSD 是：

然后对这个区间做积分，得到 RMS 噪声贡献。

所以，图上“颜色叠加”的区域不能简单地几何相加，而是 平方和再开方 得到真实值；如果某级噪声远大于其他级（如增益级 NSD ≫ ADC NSD），那在重叠区里它基本决定总噪声；如果多级噪声在同一区间相当，那么它们会 以平方和增加总 RMS。

简单来说两个相等的独立噪声源 → RMS 提高 √2 ≈ 1.41 倍，要把关键带宽内的“主导噪声”压低，确保总 SNR 足够。

计算一下

把 0–110 MHz 分成三段：

0–6.3 MHz：gain + ADC + buffer 同时存在

6.3–7.5 MHz：ADC + buffer

7.5–110 MHz：只有 buffer

在每个频段，总功率谱密度 = 各源 PSD 之和（互不相关噪声功率相加）： （单位 V/Hz） 该段噪声功率

把三个频段的功率相加，再开根号得到 总 RMS。

这和“分别对每级在自己的 NBW 内积分，然后功率求和”的结果一致：

代入图 5 的数值

增益级：NSD = 19 nV/√Hz，NBW = 6.3 MHz

缓冲级：NSD = 2 nV/√Hz，NBW = 110 MHz

ADC：NSD = 16.8 nV/√Hz，NBW = 7.5 MHz

结果（μV）

增益级单独：47.69

ADC 自身单独：46.01

缓冲级单独：20.98

总 RMS（含重叠、功率相加）：69.51

虽然缓冲级的 NSD 很低，但因带宽极宽，积分后也贡献了 ~21 μV_rms；增益级与 ADC 的 NSD 都较高，NBW 也不小，因此它们占据了总噪声的大头；在重叠频段内，三者的功率叠加抬高了地板，最终总 RMS 达到约 69.5 μV；这与文中“平衡得当时整链噪声 ~68 μV_rms、SNR ~92–93 dB”的量级吻合。