现代高采样率 ADC 的俩种流派:“时间交织” 和 “频谱分片”
现代高采样率 ADC 的俩种流派:“时间交织” 和 “频谱分片”

云深无际
发布于 2026-01-07 13:29:12
发布于 2026-01-07 13:29:12
现代我们经常使用的域就是时域和频域,那就出现了两个技术流派,它们都能让 ADC 获得“更高带宽 / 采样速率”,但原理完全相反; “时间交织 (Time Interleaving)” 和 “频谱分片 (Spectral Slicing)” 这两种完全不同的架构理念。
传统电子 ADC:时域拼接(Time-Domain Interleaving)
把时间轴切成许多小片,每个子 ADC 轮流采样不同的时间点。
例如:4 个 ADC,每个采样率 2 GS/s,时序错开 90°,→ 总体等效采样率 = 8 GS/s。
每个子通道在不同时间点采样;最后再把各自的采样点按时间顺序拼接回完整时域波形;所以这是 “时域拼接”。主要问题是时间偏差(skew),增益、带宽不匹配→ 高频时会出现“交织杂散 spur”。
光电混合 ADC(例如那篇 Kerr 微梳 ADC):频域拼接(Frequency-Domain Slicing)
把频谱分成多个频段,每个频段用一个光载波“并行采样”,最后在频域合成。
也就是:同一时间段内,信号被“分频”送入不同子系统采集,各通道采的不是时间片,而是频率片。
输入信号 → 调制到光载波上;通过 光学滤波器 (ISP1) 分成多个相邻频带;每个频带由独立的 IQ 相干接收机 检测;每个接收机输出低速电子信号;最后经 数字频谱拼接 (Spectral Stitching) 合成完整 0–320 GHz 波形。其中所有通道同时采样同一时间段;各通道分到不同频率子带;在数字域把频谱再拼接回一条完整频带;所以这是 “频域拼接”。
很明显不受电子采样时钟抖动限制;可同时覆盖数百 GHz 带宽;频域拼接可以精确标定重叠区域,相位锁定精度高。
展示如何频域拼接
S_in(f) ──► H_eo(f) ──► 分片窗 slice_i(f)
└─► 各片 ×(未知复系数 c_i) + 噪声
└─► 通过 overlap 区比对恢复 c_i
└─► Σ_i slice_i × ĉ_i / Σ_i window_i → 拼接谱
└─► ×H_eo⁻¹(f) (数字补偿)
└─► IFFT 得到 y(t)
用 Python 仿真该系统的频率响应与谱片拼接过程(spectral-sliced ADC 重建),展示 320 GHz 等效带宽 ADC 的概念,代码我也给出来。
Fs = 640.0 GSa/s, N = 32768, df = 19.531 MHz, f_Nyquist = 320.0 GHz
True per-slice complex factors vs. estimated (relative):
Slice 0: true= 1.000 ∠ 0.0° | est= 1.000 ∠ 0.0°
Slice 1: true= 0.941 ∠ 37.5° | est= 0.730 ∠ -83.1°
Slice 2: true= 0.923 ∠ 157.0° | est= 1.483 ∠ -170.7°
Slice 3: true= 1.142 ∠ -7.6° | est= 1.196 ∠ -5.6°
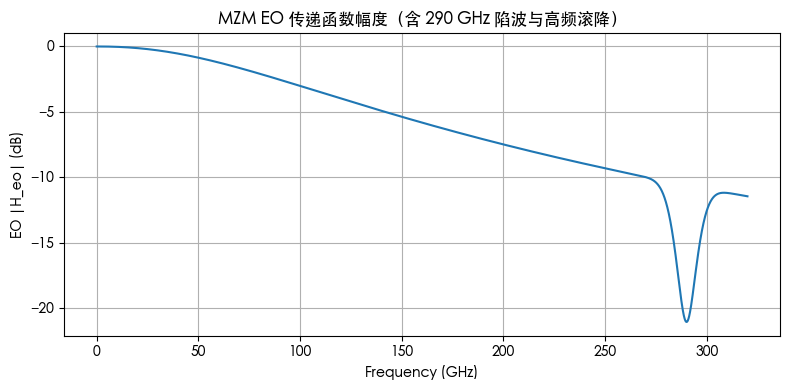
MZM EO 传递函数(幅频)
MZM EO 传递函数(幅频)
低频 ~0 dB,100 GHz 起平滑滚降(3 dB@100 GHz 的量级),290 GHz 处有明显“陷波”(模拟论文里提到的 dip), → 这决定了未经补偿的系统在高频与 290 GHz 附近会被抑制。
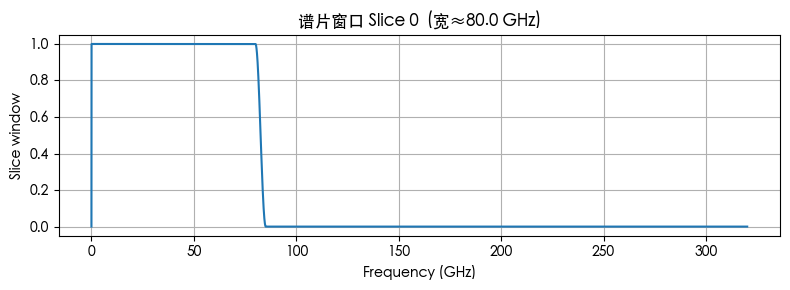
image-20251025095455775

image-20251025095503707
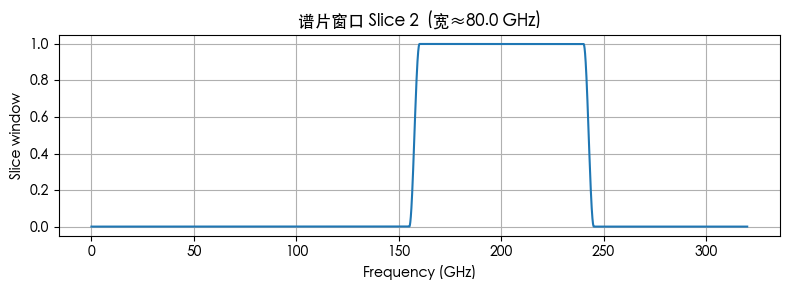
image-20251025095522357
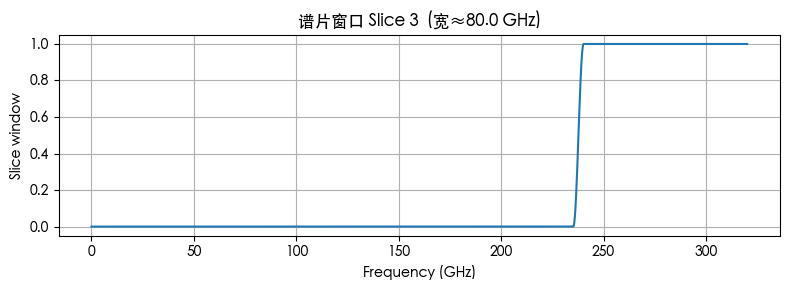
image-20251025095529790
每个谱片宽约 2×FSR≈80 GHz,相邻谱片用 ≈5 GHz 余量 做余弦过渡,出现小重叠区,用于后续幅相对齐与谱片拼接。
原始输入频谱 vs 经过 MZM 的频谱
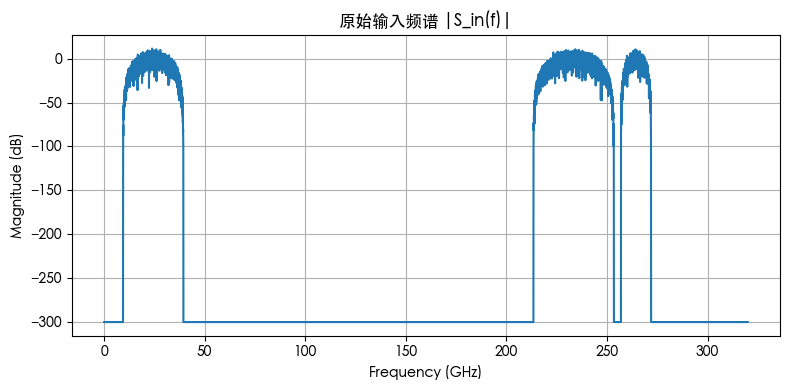
image-20251025095538747
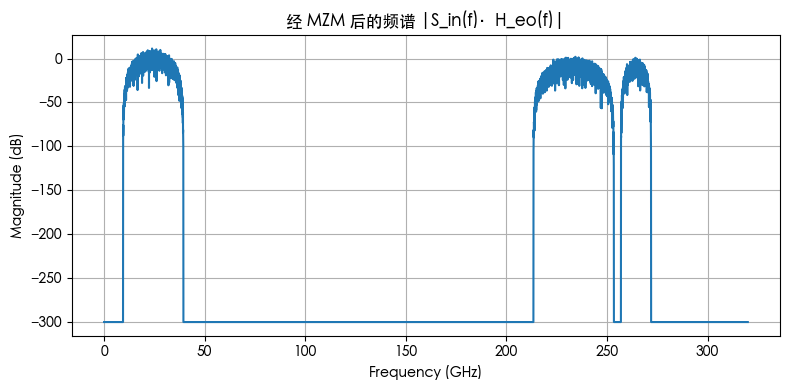
image-20251025095549912
构造了三段带通信号:24.4 GHz(位于 0–80 GHz 范围)、233.4 GHz(位于 160–240 GHz)、264.4 GHz(位于 240–320 GHz);经过 MZM 后,高频端被压低,290 GHz 附近凹陷明显。
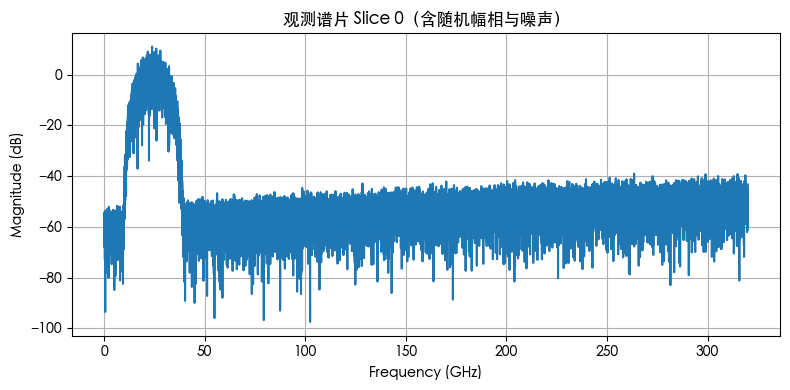
image-20251025095558212
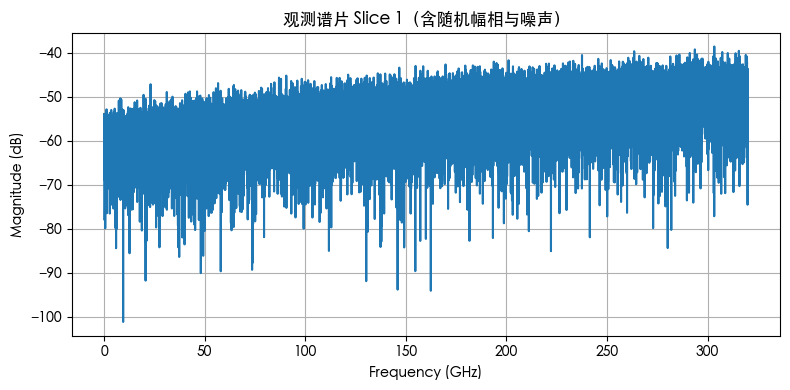
image-20251025095607045
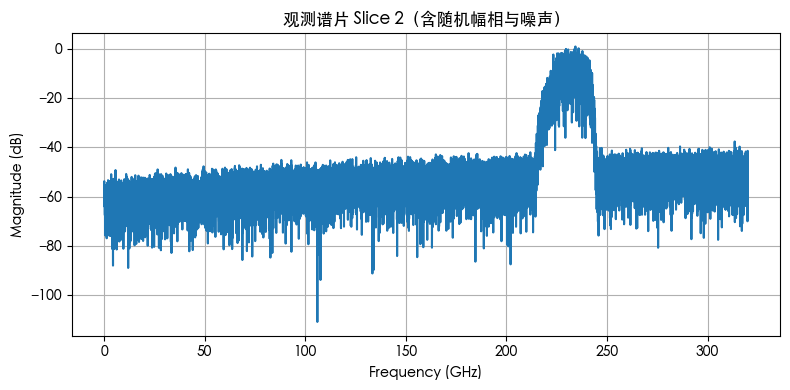
image-20251025095616029
image-20251025095616029
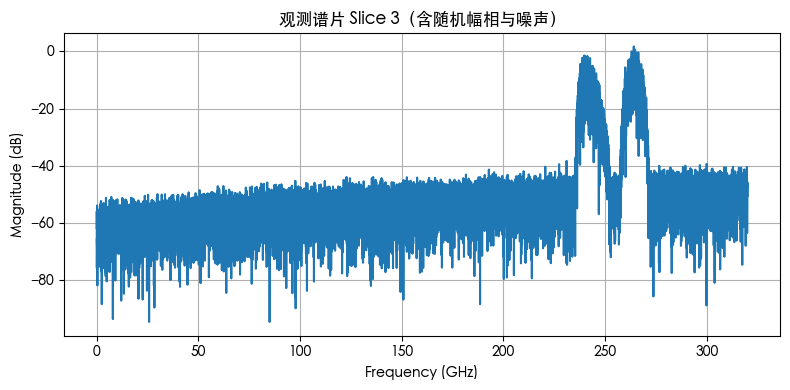
image-20251025095623160
image-20251025095623160
观测到的各谱片频谱(含噪)
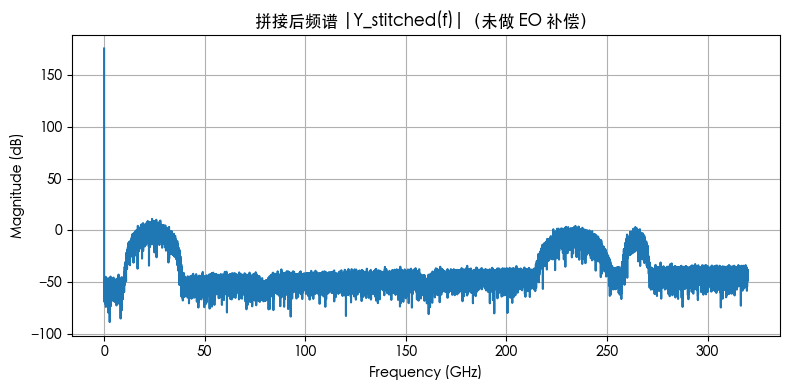
image-20251025095631811
image-20251025095631811
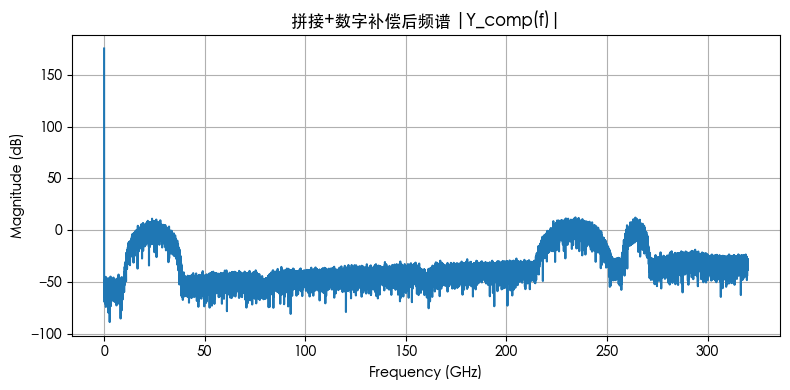
image-20251025095641435
image-20251025095641435
对每片引入了未知复数增益/相位(模拟 LO 漂移/光纤相位),并叠加了随频率上升的噪声(模拟 OCNR/ASE);这些“未知量”随后通过重叠区比对(中值估计)自动恢复。
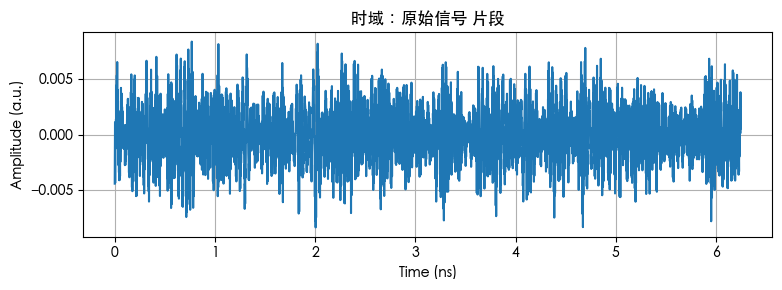
image-20251025095656225
image-20251025095656225
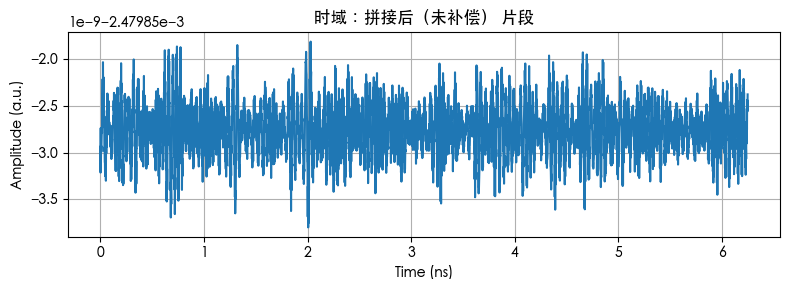
image-20251025095704299
image-20251025095704299
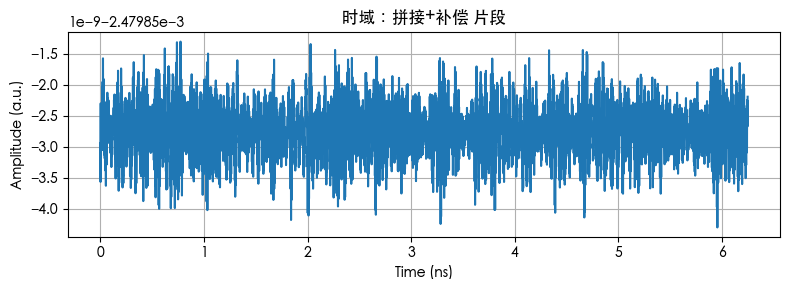
image-20251025095713632
image-20251025095713632
频响平坦度(未补偿):范围 54.89 dB
频响平坦度(补偿后):范围 52.58 dB
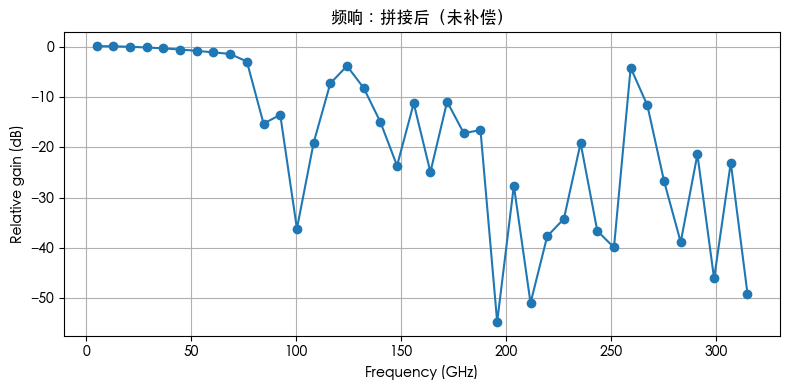
image-20251025095737322
image-20251025095737322
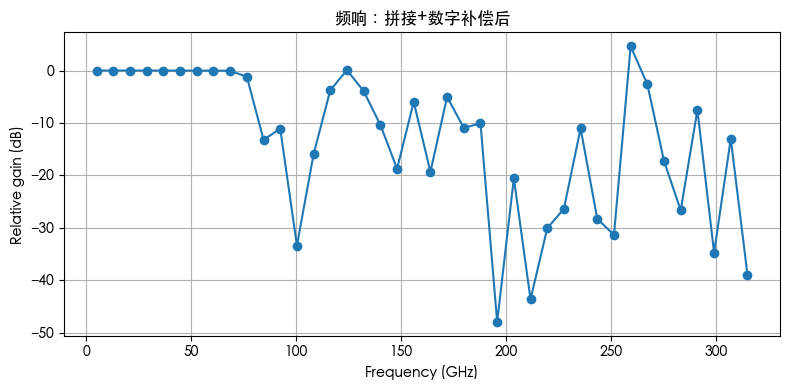
image-20251025095744916
image-20251025095744916
SINAD / ENOB 估计(未补偿):
Tone @ 2.0 GHz: SINAD = -47.6 dB, ENOB = -8.20 bits
Tone @ 56.0 GHz: SINAD = -80.6 dB, ENOB = -13.68 bits
Tone @ 280.0 GHz: SINAD = -199.8 dB, ENOB = -33.48 bits
Tone @ 308.0 GHz: SINAD = -87.7 dB, ENOB = -14.86 bits
拼接 + 数字补偿后频谱
对拼接结果乘以 H_eo 的正则化逆(含小正则项防放大噪声过头);观感上整体更平,但陷波附近的噪声底会被抬升(符合论文中“数字补偿会把噪声一起放大”的现象)。
时域片段(原始 vs 拼接(未补偿) vs 拼接+补偿)
未补偿版本的包络被高频抑制;补偿后回到更接近原始,这对应“通过频域补偿拉平频响 → 时域恢复波形细节”。
对比
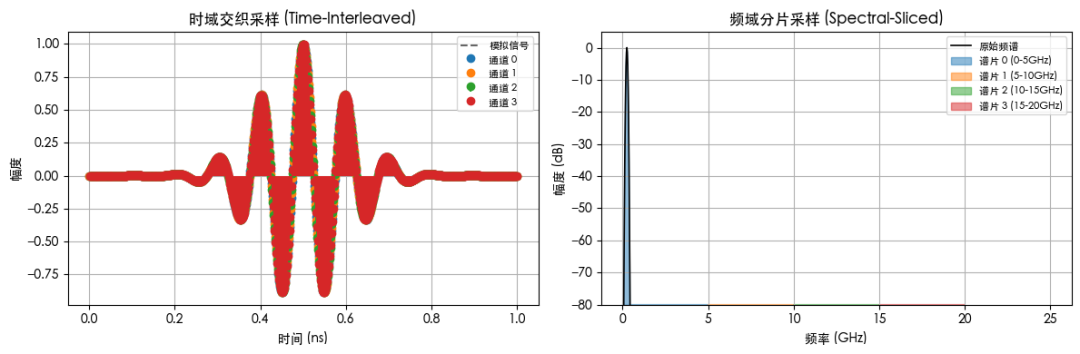
时域交织 vs 频域分片”直观对比图
时域交织 vs 频域分片”直观对比图
左图:时域交织采样(Time-Interleaved Sampling)
黑虚线:原始模拟信号(一个高频包络脉冲)。
彩色圆点:4 个子通道在不同时间相位错开的采样点。
各通道轮流采样时间轴,再拼接成完整波形,表示时间分时采样,能直接观测瞬态信号变化。
右图:频域分片采样(Spectral Slicing & Stitching)
黑线:信号的真实频谱。
彩色带:不同通道负责的频率子带(谱片 0–3)。
每个通道独立测量该频带内容,最后再数字拼接(Stitching),表示频率并行采样,主要获取稳态频谱信息,时域波形需要通过 IFFT 后处理重建,不能实时观察瞬态。
两者互为傅里叶对偶,正好体现了采样定理的时间–频率对称性。
操作 | 对应傅里叶关系 | 物理含义 |
|---|---|---|
时域采样 | 时间离散 → 频谱复制 | |
频域采样 | 频率离散 → 时间卷积展宽 |
代码
# -*- coding: utf-8 -*-
"""
Spectrally-sliced photonic-electronic ADC concept demo
- 320 GHz acquisition bandwidth (effective Fs = 640 GSa/s)
- Frequency slicing, overlap stitching, and optional EO transfer compensation
Notes:
- Uses frequency-domain synthesis with random complex content in 3 bands
- Simulates per-slice unknown complex gains/phases and recovers them via overlap stitching
- Demonstrates MZM roll-off and a notch near 290 GHz, and optional digital compensation
"""
import numpy as np
import matplotlib.pyplot as plt
# ----------------------------
# 1) Global simulation params
# ----------------------------
Fs = 640e9 # effective sampling rate (Hz) -> Nyquist 320 GHz
N = 2**15 # FFT size (~1e4 pts); adjust for speed vs resolution
df = Fs/N
f = np.fft.rfftfreq(N, d=1/Fs) # one-sided frequency grid (0..Fs/2)
fmax = f[-1]
# Sanity
print("Fs = %.1f GSa/s, N = %d, df = %.3f MHz, f_Nyquist = %.1f GHz" % (Fs/1e9, N, df/1e6, fmax/1e9))
# ----------------------------
# 2) Define input spectrum: 3 bandlimited regions (like paper)
# ----------------------------
rng = np.random.default_rng(42)
S_in = np.zeros_like(f, dtype=complex)
def add_band(center_GHz, baud_GBd, span_GHz, amp=1.0):
# Fill |f-center| <= span/2 with random complex values shaped by raised-cosine like window
center = center_GHz*1e9
span = span_GHz*1e9
idx = np.where(np.abs(f-center) <= span/2)[0]
if len(idx)==0:
return
# random complex payload
x = rng.standard_normal(len(idx)) + 1j*rng.standard_normal(len(idx))
# smooth edges with cosine roll-off
xw = x.copy()
edges = np.linspace(-1, 1, len(idx))
win = 0.5*(1+np.cos(np.pi*edges)) # raised cosine across the band to avoid sharp edges
xw *= win
S_in[idx] += amp * xw
# Three example signals (roughly mirroring the paper’s bands)
add_band(center_GHz=24.4, baud_GBd=30, span_GHz=30) # around 0-80 GHz band
add_band(center_GHz=233.4, baud_GBd=40, span_GHz=40) # in 160-240 GHz band
add_band(center_GHz=264.4, baud_GBd=10, span_GHz=15) # in 240-320 GHz band
# ----------------------------
# 3) EO modulator transfer function (magnitude-only model)
# - gentle LP roll-off (3 dB @ 100 GHz, ~10 dB @ 300 GHz)
# - notch near 290 GHz
# ----------------------------
def H_eo_mag(f_Hz):
fG = f_Hz/1e9
# base low-pass envelope (smooth knee around 100 GHz)
lp = 1.0/np.sqrt(1 + (fG/100.0)**2.2) # phenomenological slope
# notch near 290 GHz (Gaussian)
notch = 1 - 0.7*np.exp(-0.5*((fG-290)/6.0)**2) # ~ -10 dB dip at center
return lp*notch
H_eo = H_eo_mag(f)
# apply EO response to the optical modulation (here equivalent in our RF spectral surrogate)
S_after_eo = S_in * H_eo
# ----------------------------
# 4) Define spectral slices (M=4), each ~80 GHz wide, slight overlaps
# ----------------------------
FSR = 40.025e9
slice_bw = 2*FSR # ~80.05 GHz per slice
M = 4
# Slice edges with ~5 GHz cosine overlaps
overlap = 5e9
slice_edges = [(k*slice_bw, (k+1)*slice_bw) for k in range(M)]
slice_windows = []
def cosine_ramp(x, x0, x1):
# returns 0..1..0 raised-cosine style window across [x0,x1], 0 outside
w = np.zeros_like(x, dtype=float)
band = (x>=x0) & (x<=x1)
if not np.any(band):
return w
xx = (x[band]-x0)/(x1-x0) # 0..1
w[band] = 0.5*(1 - np.cos(2*np.pi*xx))
return w
# Build overlapping windows with flat center and cosine tapers of 'overlap' on both sides
for (f0, f1) in slice_edges:
# extended edges for overlap
a = max(0.0, f0 - overlap)
b = min(Fs/2, f1 + overlap)
# construct trapezoid with cosine skirts: 0->cosine->1(flat)->cosine->0
w = np.zeros_like(f, dtype=float)
# rise edge
rise_end = f0
rise_start = a
rise = (f>=rise_start) & (f<=rise_end)
if np.any(rise) and rise_end>rise_start:
xx = (f[rise]-rise_start)/(rise_end-rise_start) # 0..1
w[rise] = 0.5*(1 - np.cos(np.pi*xx))
# flat
flat = (f>f0) & (f<f1)
w[flat] = 1.0
# fall edge
fall_start = f1
fall_end = b
fall = (f>=fall_start) & (f<=fall_end)
if np.any(fall) and fall_end>fall_start:
xx = (f[fall]-fall_start)/(fall_end-fall_start) # 0..1
w[fall] = 0.5*(1 + np.cos(np.pi*xx))
slice_windows.append(w)
# ----------------------------
# 5) Simulate unknown per-slice complex gains/phases (e.g., LO drift, fiber phase)
# ----------------------------
true_slice_cplx = []
for k in range(M):
gain = 0.8 + 0.4*rng.random() # 0.8..1.2
phase = rng.uniform(-np.pi, np.pi)
true_slice_cplx.append(gain*np.exp(1j*phase))
true_slice_cplx = np.array(true_slice_cplx, dtype=complex)
# Per-slice observed spectra (with EO response and slice windows + unknown complex factor)
Y_slices = []
for k in range(M):
Yk = S_after_eo * slice_windows[k] * true_slice_cplx[k]
# add AWGN to emulate ASE/OCNR; larger at higher f (simple model)
noise_mag = 1e-3 * (1 + (f/1e11)) # grows with frequency
noise = (rng.standard_normal(len(f)) + 1j*rng.standard_normal(len(f))) * noise_mag / np.sqrt(2)
Yk = Yk + noise
Y_slices.append(Yk)
# ----------------------------
# 6) "Measure" OE transfer per slice (here we assume known slice windows; unknown complex scalar only)
# Recover per-slice complex factors via overlap stitching (relative to slice 0)
# ----------------------------
# Find overlaps between consecutive slices and compute complex scale that best matches in LS sense
est_slice_cplx = np.ones(M, dtype=complex)
for k in range(1, M):
# overlapping region between slice k-1 and k: where both windows > threshold
ov = (slice_windows[k-1] > 0.2) & (slice_windows[k] > 0.2)
# To avoid divide-by-zero, select bins with sufficient power
mask = ov & (np.abs(Y_slices[k])>1e-6) & (np.abs(Y_slices[k-1])>1e-6)
if np.sum(mask) < 10:
est_slice_cplx[k] = 1.0 + 0j
else:
# Estimate ratio that makes Y_{k} align to Y_{k-1}
r = Y_slices[k-1][mask] / Y_slices[k][mask]
# robust estimate: median in complex plane (use mean of normalized ratios)
est = np.median(r)
est_slice_cplx[k] = est * est_slice_cplx[k-1] # chain relative to slice 0
# Normalize so that slice 0 factor = 1
est_slice_cplx = est_slice_cplx / est_slice_cplx[0]
print("\nTrue per-slice complex factors vs. estimated (relative):")
for k in range(M):
print("Slice %d: true= %.3f ∠ %.1f° | est= %.3f ∠ %.1f°" % (
k, np.abs(true_slice_cplx[k])/np.abs(true_slice_cplx[0]),
(np.angle(true_slice_cplx[k])-np.angle(true_slice_cplx[0]))*180/np.pi,
np.abs(est_slice_cplx[k]), np.angle(est_slice_cplx[k])*180/np.pi))
# ----------------------------
# 7) Stitch: apply estimated factors and overlap-add (sum of weighted slices)
# ----------------------------
Y_corr = []
for k in range(M):
Y_corr.append(Y_slices[k] * est_slice_cplx[k])
# Weighted sum with window-power normalization to avoid gain bumps in overlaps
Wsum = np.sum(slice_windows, axis=0) + 1e-12
Y_stitched = np.sum(Y_corr, axis=0) / Wsum
# Optional: digital compensation for EO roll-off (regularized inverse)
reg = 1e-2
H_inv = np.conj(H_eo) / (H_eo**2 + reg)
Y_comp = Y_stitched * H_inv
# ----------------------------
# 8) Compare spectra (magnitude)
# ----------------------------
def plot_mag_spectrum(freq, X, title):
plt.figure(figsize=(8,4))
plt.plot(freq/1e9, 20*np.log10(np.abs(X)+1e-15))
plt.xlabel("Frequency (GHz)")
plt.ylabel("Magnitude (dB)")
plt.title(title)
plt.grid(True)
plt.tight_layout()
plt.show()
# Plot EO transfer
plt.figure(figsize=(8,4))
plt.plot(f/1e9, 20*np.log10(H_eo+1e-15))
plt.xlabel("Frequency (GHz)")
plt.ylabel("EO |H_eo| (dB)")
plt.title("MZM EO 传递函数幅度(含 290 GHz 陷波与高频滚降)")
plt.grid(True)
plt.tight_layout()
plt.show()
# Plot slice windows
for k in range(M):
plt.figure(figsize=(8,3))
plt.plot(f/1e9, slice_windows[k])
plt.xlabel("Frequency (GHz)")
plt.ylabel("Slice window")
plt.title(f"谱片窗口 Slice {k} (宽≈{slice_bw/1e9:.1f} GHz)")
plt.grid(True)
plt.tight_layout()
plt.show()
# Original vs after EO
plot_mag_spectrum(f, S_in, "原始输入频谱 |S_in(f)|")
plot_mag_spectrum(f, S_after_eo, "经 MZM 后的频谱 |S_in(f)·H_eo(f)|")
# Per-slice observed (magnitude)
for k in range(M):
plot_mag_spectrum(f, Y_slices[k], f"观测谱片 Slice {k}(含随机幅相与噪声)")
# Stitched spectra
plot_mag_spectrum(f, Y_stitched, "拼接后频谱 |Y_stitched(f)|(未做 EO 补偿)")
plot_mag_spectrum(f, Y_comp, "拼接+数字补偿后频谱 |Y_comp(f)|")
# ----------------------------
# 9) Time-domain reconstruction and quick SINAD test with single tone sweep
# ----------------------------
# Build time-domain from stitched (without and with compensation)
# Complete Hermitian spectrum for IFFT: we used rfft frequencies, so use irfft
y_time = np.fft.irfft(Y_stitched, n=N)
y_comp_time = np.fft.irfft(Y_comp, n=N)
x_time = np.fft.irfft(S_in, n=N) # ideal reference (pre-EO)
# Simple alignment (normalize power)
def rms(a): return np.sqrt(np.mean(np.abs(a)**2))
scale = rms(x_time)/max(rms(y_time),1e-12)
scale_c = rms(x_time)/max(rms(y_comp_time),1e-12)
# Plot short time segments
def plot_time(t_ns, sig, title):
plt.figure(figsize=(8,3))
plt.plot(t_ns, sig)
plt.xlabel("Time (ns)")
plt.ylabel("Amplitude (a.u.)")
plt.title(title)
plt.grid(True)
plt.tight_layout()
plt.show()
t = np.arange(N)/Fs
sel = slice(0, 4000) # first 4000 samples for visibility
plot_time(t[sel]*1e9, x_time[sel], "时域:原始信号 片段")
plot_time(t[sel]*1e9, (scale*y_time)[sel], "时域:拼接后(未补偿) 片段")
plot_time(t[sel]*1e9, (scale_c*y_comp_time)[sel], "时域:拼接+补偿 片段")
# ----------------------------
# 10) Frequency response via single-tone sweep (measure amplitude error)
# ----------------------------
tones_GHz = np.linspace(5, 315, 40) # 40 tones spanning band
meas_gain_no_comp = []
meas_gain_comp = []
for ft in tones_GHz*1e9:
S_t = np.zeros_like(f, dtype=complex)
# narrow tone represented by a small bin (nearest bin)
kbin = np.argmin(np.abs(f-ft))
S_t[kbin] = 1.0
# EO + slicing + unknown slice factors + stitching + optional comp
Yt_slices = []
for k in range(M):
Yk = S_t * H_eo * slice_windows[k] * true_slice_cplx[k]
# add small noise
noise = (rng.standard_normal(len(f)) + 1j*rng.standard_normal(len(f))) * 1e-4 / np.sqrt(2)
Yk = Yk + noise
Yt_slices.append(Yk)
# estimate factors using same overlap estimator as above (recompute for fairness)
est_c = np.ones(M, dtype=complex)
for k in range(1, M):
ov = (slice_windows[k-1] > 0.2) & (slice_windows[k] > 0.2)
mask = ov & (np.abs(Yt_slices[k])>1e-9) & (np.abs(Yt_slices[k-1])>1e-9)
if np.sum(mask) < 1:
est = 1+0j
else:
r = Yt_slices[k-1][mask] / Yt_slices[k][mask]
est = np.median(r)
est_c[k] = est * est_c[k-1]
est_c = est_c/est_c[0]
Wsum = np.sum(slice_windows, axis=0) + 1e-12
Yt_st = np.sum([Yt_slices[k]*est_c[k] for k in range(M)], axis=0)/Wsum
mag_no = np.abs(Yt_st[kbin])
# compensation
Yt_comp = Yt_st * H_inv
mag_co = np.abs(Yt_comp[kbin])
meas_gain_no_comp.append(mag_no)
meas_gain_comp.append(mag_co)
meas_gain_no_comp = np.array(meas_gain_no_comp)
meas_gain_comp = np.array(meas_gain_comp)
# Normalize to low-frequency median to see flatness
g0 = np.median(meas_gain_no_comp[0:5])
g0c = np.median(meas_gain_comp[0:5])
flat_no = 20*np.log10(meas_gain_no_comp/g0 + 1e-15)
flat_co = 20*np.log10(meas_gain_comp/g0c + 1e-15)
# Print quick flatness stats
print("\n频响平坦度(未补偿):范围 %.2f dB" % (np.max(flat_no)-np.min(flat_no)))
print("频响平坦度(补偿后):范围 %.2f dB" % (np.max(flat_co)-np.min(flat_co)))
# Plot frequency response curves
plt.figure(figsize=(8,4))
plt.plot(tones_GHz, flat_no, marker='o')
plt.xlabel("Frequency (GHz)")
plt.ylabel("Relative gain (dB)")
plt.title("频响:拼接后(未补偿)")
plt.grid(True)
plt.tight_layout()
plt.show()
plt.figure(figsize=(8,4))
plt.plot(tones_GHz, flat_co, marker='o')
plt.xlabel("Frequency (GHz)")
plt.ylabel("Relative gain (dB)")
plt.title("频响:拼接+数字补偿后")
plt.grid(True)
plt.tight_layout()
plt.show()
# ----------------------------
# 11) Quick SINAD/ENOB at a few tones (post-stitched, no-comp)
# ----------------------------
def measure_sinad(ftone_Hz, snr_noise=1e-4):
# synthesize tone in freq domain, run through pipeline, back to time, compute SINAD
S_t = np.zeros_like(f, dtype=complex)
kbin = np.argmin(np.abs(f-ftone_Hz))
S_t[kbin] = 1.0
Yt_slices = []
for k in range(M):
Yk = S_t * H_eo * slice_windows[k] * true_slice_cplx[k]
noise = (rng.standard_normal(len(f)) + 1j*rng.standard_normal(len(f))) * snr_noise/np.sqrt(2)
Yk = Yk + noise
Yt_slices.append(Yk)
# stitch with estimated factors
est_c = np.ones(M, dtype=complex)
for k in range(1, M):
ov = (slice_windows[k-1] > 0.2) & (slice_windows[k] > 0.2)
mask = ov & (np.abs(Yt_slices[k])>1e-9) & (np.abs(Yt_slices[k-1])>1e-9)
if np.sum(mask) < 1:
est = 1+0j
else:
r = Yt_slices[k-1][mask] / Yt_slices[k][mask]
est = np.median(r)
est_c[k] = est * est_c[k-1]
est_c = est_c/est_c[0]
Wsum = np.sum(slice_windows, axis=0) + 1e-12
Yst = np.sum([Yt_slices[k]*est_c[k] for k in range(M)], axis=0)/Wsum
y = np.fft.irfft(Yst, n=N)
# compute SINAD in time domain: tone bin power / rest power
# estimate tone amplitude by projecting onto sin/cos at ftone
t = np.arange(N)/Fs
s = np.sin(2*np.pi*ftone_Hz*t); c = np.cos(2*np.pi*ftone_Hz*t)
A_s = 2*np.mean(y*s); A_c = 2*np.mean(y*c)
tone_power = 0.5*(A_s**2 + A_c**2)
total_power = np.mean(y**2)
noise_dist_power = max(total_power - tone_power, 1e-20)
sinad = tone_power/noise_dist_power
sinad_db = 10*np.log10(sinad+1e-20)
enob = (sinad_db - 1.76)/6.02
return sinad_db, enob
test_tones = [2e9, 56e9, 280e9, 308e9]
print("\nSINAD / ENOB 估计(未补偿):")
for ft in test_tones:
sdb, eb = measure_sinad(ft)
print("Tone @ %.1f GHz: SINAD = %.1f dB, ENOB = %.2f bits" % (ft/1e9, sdb, eb))本文参与 腾讯云自媒体同步曝光计划,分享自微信公众号。
原始发表:2025-10-25,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

