数据结构(C语言篇):(十九)归并排序和非比较排序
前言
归并排序作为分治策略的经典实现,通过递归分解与有序合并确保最坏情况下仍保持O(n log n)的时间复杂度,成为稳定排序的标杆。而非比较排序(如计数排序、桶排序)突破了基于元素比较的理论下限,在特定数据范围内可实现线性时间复杂度,但依赖数据的分布特征。这两种技术路线的本质差异——比较与映射——揭示了算法设计中对时间与空间权衡的不同思考维度,也为工程实践中根据数据特征选择算法提供了理论依据。下面就让我们正式进入今天的学习吧!
一、归并排序
1.1 算法思想
归并排序(Merge Sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每一个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,就称为二路归并。归并算法的核心思想如下:
- 分解(Divide):将待排序的数组递归地分割成两个规模大致相等的子数组,直到每个子数组只包含一个元素(单个元素天然有序)。
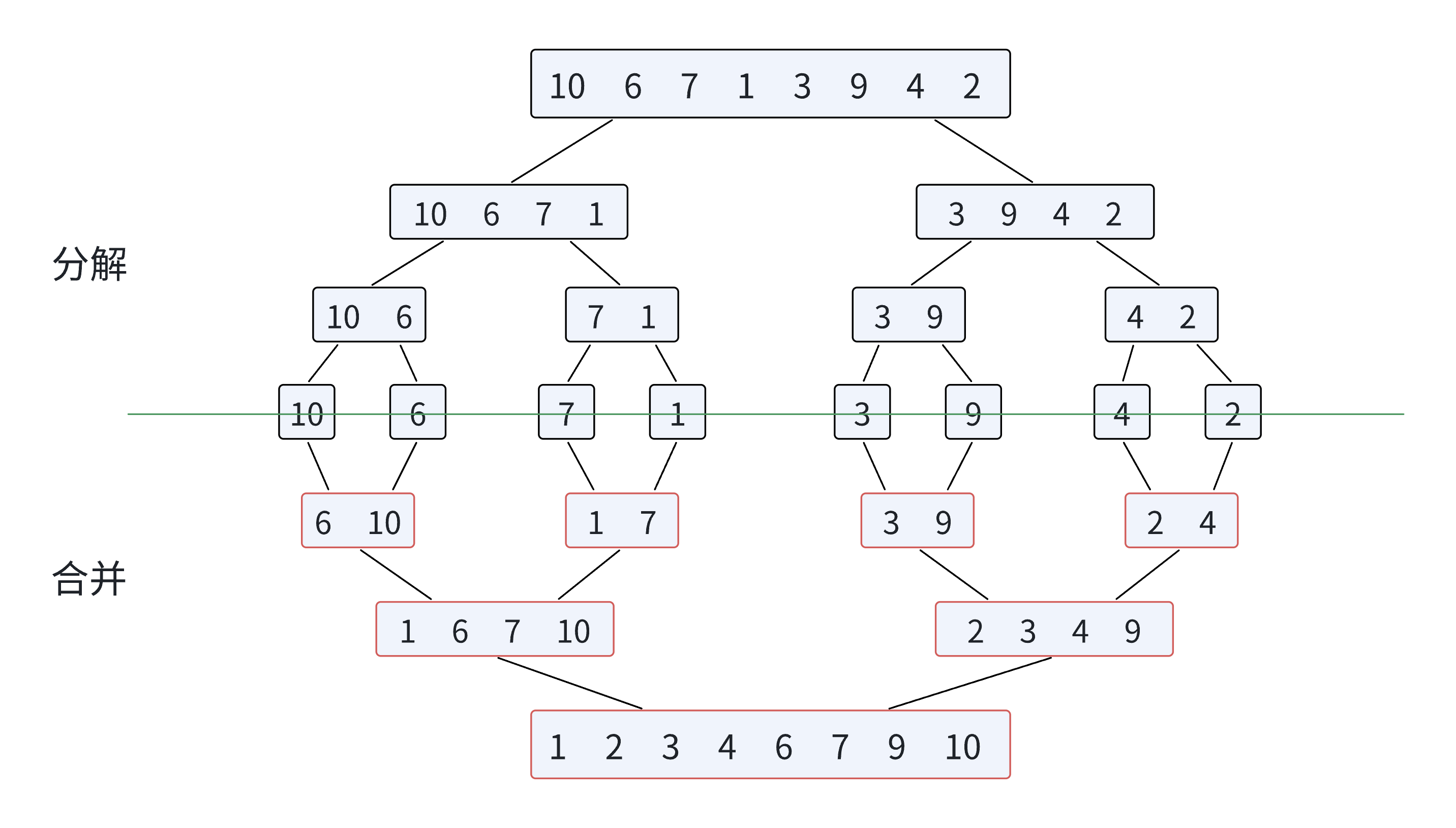
例如,对数组
[8, 4, 5, 7, 1, 3, 6, 2]分解:第一轮分割为[8,4,5,7]和[1,3,6,2];第二轮分割为[8,4]、[5,7]、[1,3]、[6,2];第三轮分割为[8]、[4]、[5]、[7]、[1]、[3]、[6]、[2](此时所有子数组都只含一个元素)。 - 合并(Merge):将已排序的子数组逐步合并,每次合并两个有序子数组为一个更大的有序数组,直到最终合并为一个完整的有序数组。
合并的关键是 “双指针法”:对两个有序子数组
left和right,分别设置指针i和j指向起始位置,创建一个临时数组temp;比较left[i]和right[j],将较小的元素放入temp并移动对应指针;当一个子数组遍历完后,将另一个子数组的剩余元素直接复制到temp;最后将temp中的元素复制回原数组,完成合并。
我将核心步骤以流程图的形式为大家展示如下:
1.2 代码实现
// 合并两个有序子数组
// arr: 原始数组
// left: 左子数组起始索引
// mid: 中间索引(左子数组结束索引)
// right: 右子数组结束索引
void merge(int arr[], int left, int mid, int right) {
int i, j, k;
int n1 = mid - left + 1; // 左子数组大小
int n2 = right - mid; // 右子数组大小
// 创建临时数组
int *L = (int*)malloc(n1 * sizeof(int));
int *R = (int*)malloc(n2 * sizeof(int));
// 复制数据到临时数组
for (i = 0; i < n1; i++)
L[i] = arr[left + i];
for (j = 0; j < n2; j++)
R[j] = arr[mid + 1 + j];
// 合并临时数组到原数组
i = 0; // 左子数组起始索引
j = 0; // 右子数组起始索引
k = left; // 合并后数组起始索引
// 比较两个子数组元素,将较小的放入原数组
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// 复制左子数组剩余元素
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// 复制右子数组剩余元素
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
// 释放临时数组内存
free(L);
free(R);
}
// 归并排序主函数
// arr: 要排序的数组
// left: 起始索引
// right: 结束索引
void mergeSort(int arr[], int left, int right) {
if (left < right) {
// 计算中间索引,避免溢出
int mid = left + (right - left) / 2;
// 递归排序左半部分
mergeSort(arr, left, mid);
// 递归排序右半部分
mergeSort(arr, mid + 1, right);
// 合并已排序的两部分
merge(arr, left, mid, right);
}
}从上面的代码中我们可以看出,归并排序的实现是依赖于两个关键函数的,分别是:
(1)mergeSort 函数(分治函数)
- 递归地将数组分成两半,直到子数组长度为 1;
- 计算中间索引的方式
mid = left + (right - left) / 2可以避免整数溢出; - 对左右两半分别递归排序后,调用 merge 函数合并。
(2)merge 函数(合并函数)
- 创建临时数组存储左右两个子数组;
- 使用双指针技术比较两个子数组的元素,将较小的元素放入原数组;
- 处理剩余未合并的元素(当一个子数组已完全合并,另一个还有剩余元素时);
- 释放临时数组占用的内存。
1.3 时间复杂度计算
要计算归并排序的时间复杂度,我们可以把归并排序拆分成两个过程:
- 分解过程:将数组分成两半的过程可以形成一棵二叉树,树的深度为
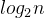
log_2n
;
- 合并过程:每一层的合并操作总共需要
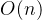
O (n)
时间(每个元素都被处理一次)。
因此,归并排序总的时间复杂度为:
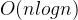
O (n log n)
1.4 排序算法的性能对比
我们来通过一段代码,比较并分析我们目前为止学过的排序算法的性能:
// 测试排序的性能对⽐
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int)*N);
int* a2 = (int*)malloc(sizeof(int)*N);
int* a3 = (int*)malloc(sizeof(int)*N);
int* a4 = (int*)malloc(sizeof(int)*N);
int* a5 = (int*)malloc(sizeof(int)*N);
int* a6 = (int*)malloc(sizeof(int)*N);
int* a7 = (int*)malloc(sizeof(int)*N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N-1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
BubbleSort(a7, N);
int end7 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
printf("BubbleSort:%d\n", end7 - begin7);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
}我们分析代码的运行结果,可以得到以下结论:
- 快速排序(QuickSort):最快,时间最短;
- 堆排序(HeapSort):略慢于快速排序,但性能稳定;
- 归并排序(MergeSort):与堆排序接近,略慢于快速排序;
- 希尔排序(ShellSort):比上述三种算法慢,但远快于简单排序;
- 插入排序(InsertSort):明显慢于希尔排序;
- 选择排序(SelectSort):比插入排序更慢;
- 冒泡排序(BubbleSort):最慢,可能需要极长的时间。
是什么导致了上述这样的结果呢?
结果背后的原因如下:
- 时间复杂度差异: 快速排序、堆排序、归并排序:
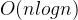
O (n log n)
,效率高; 希尔排序:
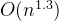
O (n^{1.3})
,介于两种复杂度之间;插入排序、选择排序、冒泡排序:
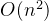
O (n^{2})
,效率低。
- 算法特性影响:
快速排序虽然最坏情况是
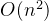
O (n^{2})
,但平均性能最优;
堆排序不需要递归,空间复杂度低,但常数因子较大;
归并排序需要额外
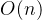
O (n)
空间,影响了实际性能;
简单排序算法(插入、选择、冒泡)在处理 10 万级数据时,
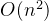
O (n^{2})
的复杂度会导致运算量达到 100 亿级别,因此耗时极长。
二、非比较排序
2.1 计数排序
计数排序又被称为鸽巢原理,是对哈希直接定址法的变形应用。它是一种非比较型排序算法,其核心思想是通过统计待排序元素中每个值出现的次数,然后根据次数信息将元素直接放置到正确的位置,从而实现排序。
与快速排序、归并排序等依赖元素间比较的算法不同,计数排序的排序过程不涉及元素比较,而是利用了 “元素值的范围有限” 这一特性,适用于整数排序或可映射为整数的离散值排序(如年龄、成绩等)。
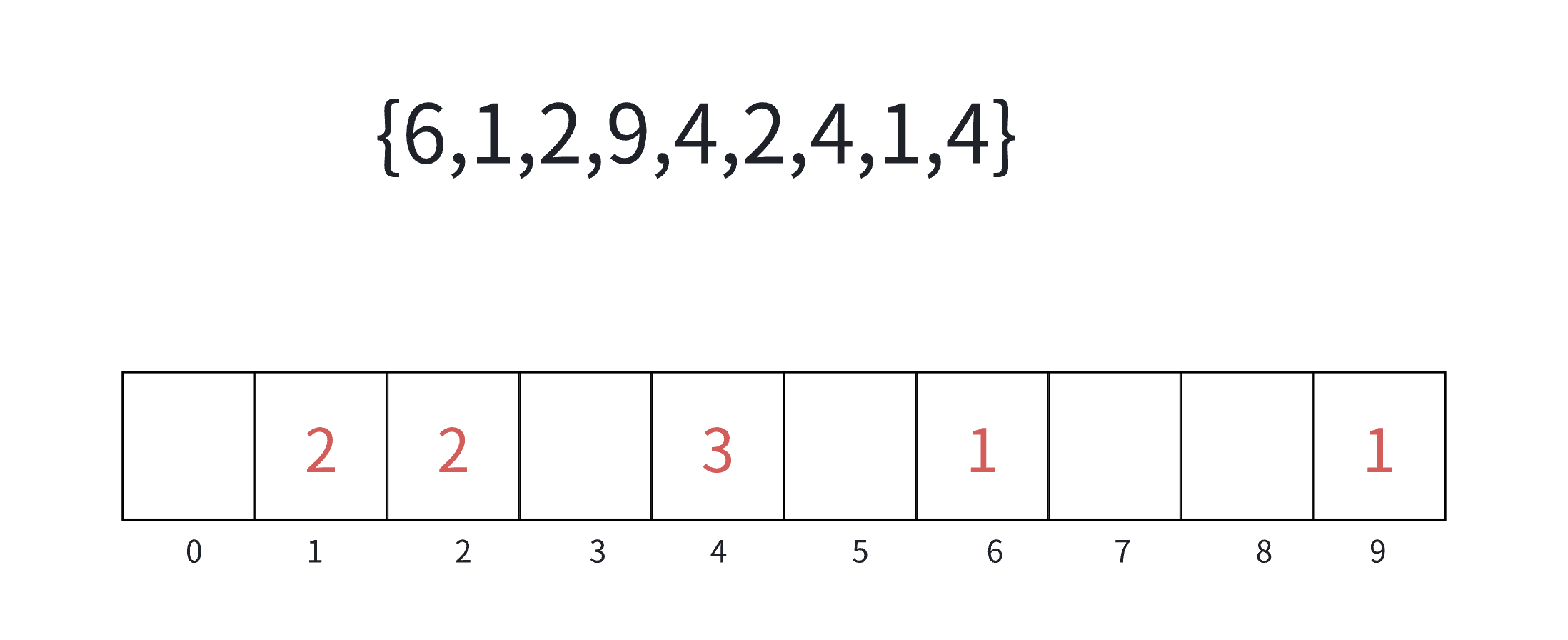
计数排序的实现步骤如下:
(1)统计相同元素出现次数;
(2)根据统计的结果将序列回收到原来的序列中。
我们可以将上述步骤画图分析如下:

下面是完整的代码实现:
// 计数排序函数
// arr: 待排序数组
// n: 数组元素个数
// 返回值: 排序后的新数组(需要手动释放内存)
int* countingSort(int arr[], int n) {
if (n <= 0) return NULL;
// 1. 找出数组中的最大值和最小值
int min = arr[0];
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] < min) {
min = arr[i];
}
if (arr[i] > max) {
max = arr[i];
}
}
// 2. 计算数据范围并创建计数数组
int range = max - min + 1;
int* count = (int*)calloc(range, sizeof(int)); // 初始化为0
if (count == NULL) {
printf("内存分配失败\n");
return NULL;
}
// 3. 统计每个元素出现的次数
for (int i = 0; i < n; i++) {
count[arr[i] - min]++; // 映射到计数数组的索引
}
// 4. 计算前缀和,确定每个元素的结束位置
for (int i = 1; i < range; i++) {
count[i] += count[i - 1];
}
// 5. 构建结果数组(倒序遍历保证稳定性)
int* result = (int*)malloc(n * sizeof(int));
if (result == NULL) {
printf("内存分配失败\n");
free(count);
return NULL;
}
for (int i = n - 1; i >= 0; i--) {
// 根据计数数组确定当前元素的位置
int index = count[arr[i] - min] - 1;
result[index] = arr[i];
count[arr[i] - min]--; // 更新计数
}
// 释放计数数组
free(count);
return result;
}2.2 计数排序的特性
(1)计数排序是唯一不依赖元素间比较的线性时间排序算法,其核心逻辑不涉及 “谁大谁小” 的判断,而是通过两个关键步骤实现排序:
- 先统计每个元素的出现次数(用计数数组记录);
- 再根据次数信息,直接将元素 “填充” 到最终的有序位置(通过前缀和确定位置)。这与快速排序、归并排序等 “比较型算法” 有本质区别 —— 后者的时间复杂度下限是
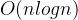
O(n log n)
,而计数排序可突破该下限,达到线性时间。
(2)计数排序的时间消耗集中在 3 个线性操作上,整体复杂度为
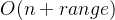
O(n + range)
(n 是元素个数,range 是数据范围,即 max - min + 1)。
(3)可实现稳定排序,但需要依赖 “倒序遍历”。计数排序的稳定性可通过 “倒序遍历原始数组” 来保证 —— 即从原始数组的最后一个元素开始,根据计数数组的前缀和确定其在结果数组的位置,然后将计数减 1。
(4)适用场景有限,仅支持 “离散整数” 或可映射为整数的数据,无法直接排序浮点数、字符串等类型。若要处理非整数数据(如 0~1 的浮点数),需先将其 “映射” 为整数(如乘以 100 转为 0~100 的整数),排序后再还原,但会损失精度。
(5)计数排序对于数据范围是及其敏感的,依赖已知且有限的数据范围。必须提前确定 min 和 max,否则无法创建计数数组。若数据是动态新增的(如实时插入新元素),计数数组的大小无法预先确定,无法动态调整,因此仅适用于 “静态数据集” 的一次性排序。
三、排序算法复杂度及稳定性分析
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且 r[i] 在 r[j] 之前,⽽在排序后的序列中, r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
冒泡排序 | 稳定 | ||||
直接选择排序 | 不稳定 | ||||
直接插入排序 | 稳定 | ||||
希尔排序 | 不稳定 | ||||
堆排序 | 不稳定 | ||||
归并排序 | 稳定 | ||||
快速排序 | 不稳定 |
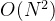
O(n^{2})
总结
本期博客是数据结构C语言篇的最后一期博客啦!我在本期博客中为大家介绍了归并排序、非比较排序,并对前几期博客中所学的排序算法进行了总结与比较。希望这个专栏的博客能给大家带来不少收获!谢谢大家一直以来对博主的支持!从下期博客开始,我将正式开始C++以及Linux相关内容的更新,请大家继续关注哦!
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2026-01-13,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

