三大主流速度规划方法对比

索旭东

发布于 2026-02-04 14:51:29

380

文章被收录于专栏：具身小站具身小站

方法一：梯形速度规划（基础但生硬）

原理：如同它的名字，速度曲线呈“梯形”。过程是：匀加速 → 匀速 → 匀减速。
优点：计算极其简单，对控制器要求低。
致命缺点：在加速开始、结束以及转向匀速的瞬间，加速度会发生跳变（想象一下瞬间推一把或拉一把）。这种力的突变就是机械臂抖动和异响的元凶。
适用：仅适用于对平滑性要求极低的低速场合。

方法二：S型速度规划（高速高精的首选）

原理：在梯形规划基础上，对加速度的变化率（Jerk） 进行约束，让加速度也能“斜坡式”地增大或减小，从而变得连续。
核心价值：速度曲线呈柔和的“S”形，加速度曲线是平滑的梯形。从根本上消除了刚性冲击，大幅减少残余振动。
调参关键：加加速度（Jerk） 的限值。调小它，运动更柔和；调大它，响应更迅速但可能更“冲”。这是调试手感的“灵魂参数”。
适用：几乎所有要求高速、高精度、低振动的场景，如精密装配、快速分拣、激光切割等。

方法三：多项式规划（灵活但复杂）

原理：使用高阶多项式函数（如3-5-3、4-3-4多项式）来拟合整个运动过程。
优点：极其灵活，可以精确设定起点和终点的位置、速度、加速度等多个边界条件。
缺点：在线计算量大，对控制器性能要求高，且参数选择不当可能导致曲线超调。
适用：需要与动力学状态（例如力控交互）进行复杂对接的特殊场合。

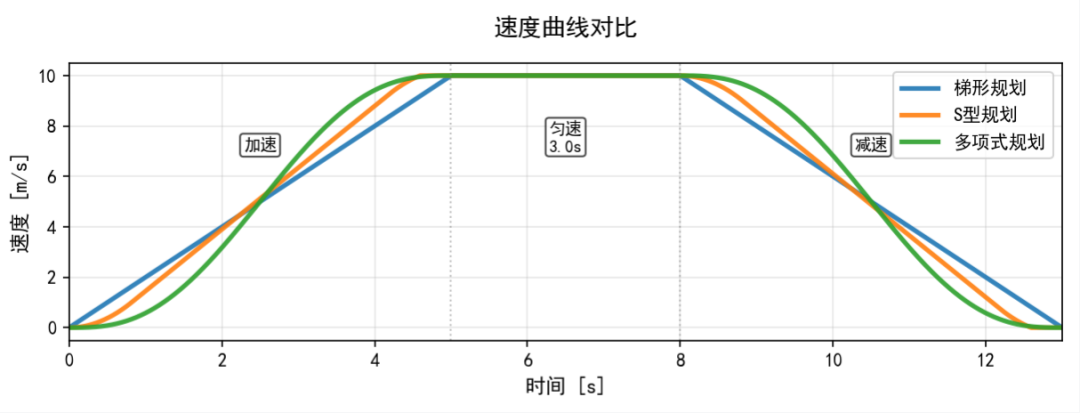
上面图形的绘制代码如下：

import numpy as np
import matplotlib.pyplot as plt
# ----------------------
# 基本参数
# ----------------------
v0 = 0.0          # 初速度
a_max = 2.0       # 最大加速度
v_max = 10.0      # 最大速度
t_acc = v_max / a_max  # 加速到最大速度的时间 = 5s
t_keep = 3.0          # 保持时间
T = t_acc + t_keep + t_acc  # 总时间 = 13s
dt = 0.001
t = np.arange(0, T + dt, dt)
# ----------------------
# 1. 梯形速度规划
# ----------------------
def trapezoid_velocity(t, v0, a_max, v_max, T):
    t_acc = v_max / a_max     # 加速时间
    t_dec_start = T - t_acc   # 减速开始时间
    
    v = np.zeros_like(t)
    for i, ti in enumerate(t):
        if ti <= t_acc:
            # 匀加速段
            v[i] = v0 + a_max * ti
        elif ti >= t_dec_start:
            # 匀减速段（对称）
            tau = T - ti
            v[i] = v0 + a_max * tau
        else:
            # 匀速段
            v[i] = v_max
    return v
v_trap = trapezoid_velocity(t, v0, a_max, v_max, T)
# ----------------------
# 2. S型速度规划（7段式，简化实现）
# ----------------------
def s_curve_velocity_simple(t, v0, v_max, a_max, T, t_acc, t_keep):
    """
    简化的S型速度规划
    确保：起点速度=0，终点速度=0，中间匀速段时间=t_keep
    """
    # 设置加加速度（控制平滑度）
    j_max = 2.5  # 加加速度，可调节
    
    # 计算各段时间（对称结构）
    # 加加速阶段时间（达到最大加速度）
    Tj = min(t_acc / 2, np.sqrt(a_max / j_max))
    
    # 加加速阶段能达到的最大加速度
    a_lim = j_max * Tj
    
    # 加速段总时间 = 加加速 + 匀加速 + 减加速
    # 实际上我们固定总加速时间 = t_acc，所以匀加速时间 = t_acc - 2*Tj
    Ta = t_acc  # 总加速时间
    
    # 计算各段实际时间
    t1 = Tj  # 加加速结束时间
    t2 = Ta - Tj  # 匀加速结束时间（也是减加速开始时间）
    t3 = Ta  # 加速段结束时间
    
    # 匀速段开始和结束时间
    t4 = Ta + t_keep  # 匀速段结束时间
    t5 = t4 + Tj  # 加减速结束时间
    t6 = T - Tj  # 匀减速结束时间
    t7 = T  # 总时间
    
    v = np.zeros_like(t)
    
    for i, ti in enumerate(t):
        if ti <= t1:
            # 1. 加加速段
            v[i] = 0.5 * j_max * ti**2
        elif ti <= t2:
            # 2. 匀加速段
            tau = ti - t1
            v[i] = 0.5 * j_max * t1**2 + a_lim * tau
        elif ti <= t3:
            # 3. 减加速段
            tau = ti - t2
            v[i] = 0.5 * j_max * t1**2 + a_lim * (t2 - t1) + a_lim * tau - 0.5 * j_max * tau**2
        elif ti <= t4:
            # 4. 匀速段
            v[i] = v_max
        elif ti <= t5:
            # 5. 加减速段（开始减速）
            tau = ti - t4
            v[i] = v_max - 0.5 * j_max * tau**2
        elif ti <= t6:
            # 6. 匀减速段
            tau = ti - t5
            v[i] = v_max - 0.5 * j_max * (t5 - t4)**2 - a_lim * tau
        elif ti <= t7:
            # 7. 减减速段
            tau = ti - t6
            v[i] = v_max - 0.5 * j_max * (t5 - t4)**2 - a_lim * (t6 - t5) - a_lim * tau + 0.5 * j_max * tau**2
        else:
            v[i] = 0
    
    # 确保速度不超过v_max且最终为0
    v = np.clip(v, 0, v_max)
    v[-1] = 0
    
    return v
v_s = s_curve_velocity_simple(t, v0, v_max, a_max, T, t_acc, t_keep)
# ----------------------
# 3. 多项式速度规划（5次多项式）
# ----------------------
def polynomial_velocity_simple(t, v0, v_max, T, t_acc, t_keep):
    """
    简化的5次多项式速度规划
    确保：起点速度=0，终点速度=0，中间匀速段时间=t_keep
    """
    # 时间分段点
    t1 = t_acc  # 加速结束
    t2 = t_acc + t_keep  # 匀速结束/减速开始
    
    v = np.zeros_like(t)
    
    for i, ti in enumerate(t):
        if ti <= t1:
            # 加速段：0 → t1，使用5次多项式
            # v(t) = v_max * (10τ^3 - 15τ^4 + 6τ^5)，其中 τ = t/t1
            τ = ti / t1
            v[i] = v_max * (10 * τ**3 - 15 * τ**4 + 6 * τ**5)
        elif ti <= t2:
            # 匀速段
            v[i] = v_max
        else:
            # 减速段：t2 → T，使用对称的5次多项式
            # τ = (T - t) / t_acc，注意时间方向
            τ = (T - ti) / t_acc
            v[i] = v_max * (10 * τ**3 - 15 * τ**4 + 6 * τ**5)
    
    # 确保终点速度为0
    v[-1] = 0
    
    return v
v_poly = polynomial_velocity_simple(t, v0, v_max, T, t_acc, t_keep)
# ----------------------
# 4. 计算加速度曲线
# ----------------------
def calculate_acceleration(v, dt):
    """通过中心差分法计算加速度"""
    a = np.zeros_like(v)
    a[1:-1] = (v[2:] - v[:-2]) / (2 * dt)
    a[0] = (v[1] - v[0]) / dt
    a[-1] = (v[-1] - v[-2]) / dt
    return a
# 计算三种规划的加速度
a_trap = calculate_acceleration(v_trap, dt)
a_s = calculate_acceleration(v_s, dt)
a_poly = calculate_acceleration(v_poly, dt)
# ----------------------
# 5. 可视化对比
# ----------------------
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 创建子图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
# 5.1 速度曲线对比
ax1 = axes[0, 0]
ax1.plot(t, v_trap, label='梯形规划', color='#1f77b4', linewidth=2.5, alpha=0.9)
ax1.plot(t, v_s, label='S型规划', color='#ff7f0e', linewidth=2.5, alpha=0.9)
ax1.plot(t, v_poly, label='多项式规划', color='#2ca02c', linewidth=2.5, alpha=0.9)
ax1.set_title('速度曲线对比', fontsize=13, fontweight='bold', pad=15)
ax1.set_xlabel('时间 [s]', fontsize=11)
ax1.set_ylabel('速度 [m/s]', fontsize=11)
ax1.grid(True, alpha=0.3)
ax1.legend(fontsize=10, loc='upper right')
ax1.set_xlim([0, T])

本文参与腾讯云自媒体同步曝光计划，分享自微信公众号。

原始发表：2026-01-27，如有侵权请联系 cloudcommunity@tencent.com 删除