将任意数目的多边形组合在一起
我有任意数量的多边形(在这种情况下是六边形)是随机排列的,但它们都在接触另一个六角。
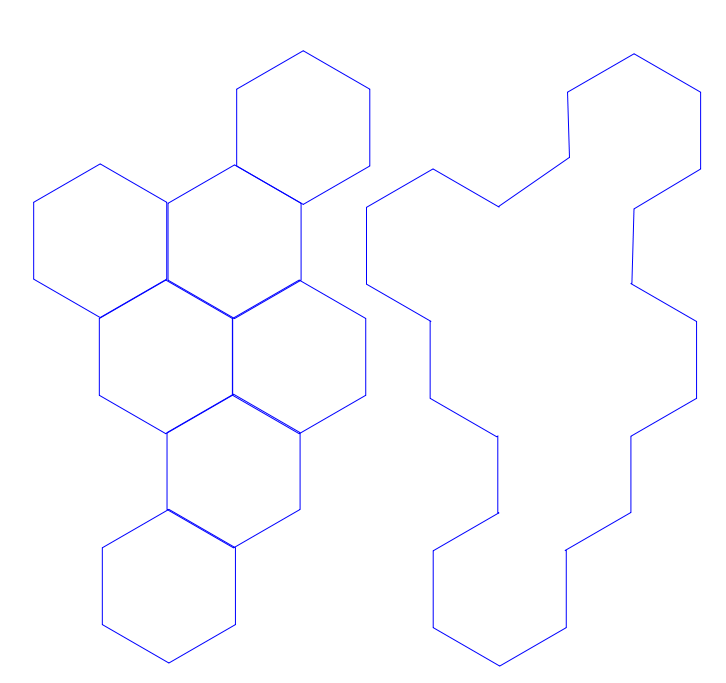
每个单独的十六进制都有6x,y点。所有的六边形都知道顶点的存在。
有人能指出一个算法的方向吗?这个算法将所有的六边形组合成一个多边形?本质上,我只是在寻找一个函数,它以一种从一条线到另一条线的方式排列出一个顶点位置数组,它形成多边形。
到目前为止,这是我的方法:
- 为所有的十六进制创建所有顶点的数组。
- 确定数组中顶点发生的次数。
- 如果顶点在数组3+时间内,则从数组中删除顶点。
- 如果顶点在数组中2次,则删除其中的一个。
不过,下一步是很棘手的。我用画布画出这些多边形,实质上是画一条从一个顶点到另一个顶点的线。因此,最终数组中顶点的顺序是非常重要的。不能武断地分类。
另外,我不是在寻找一个“凸包”算法,因为这不会正确地绘制多边形。
有这样的功能吗?我是在正确的轨道上,还是有更好的更有效的方式?
回答 3
Stack Overflow用户
发布于 2012-12-01 15:08:22
我会这样做:
- 把所有的都列出来。边由两对坐标定义。
- 如果任何一方不止一次出现,则移除该侧的所有实例。
- 挑一个任意的一面,然后从那一边选择一个点。
- 将该点放置在数组中。
- 按照当前的方向,在数组中放置另一个点。
- 删除你刚才跟着的那一边。
- 然后查找另一侧的点,该点与数组中的最后一个点相同。只有一个这样的一面。如果没有,你就完蛋了。
- 回到第5步。
您现在应该有一个数组的点组成,按照顺序,你想要的形状。
只是要注意这不会处理洞。形状必须由一条路径来定义。
Stack Overflow用户
发布于 2012-12-01 16:27:17
如果不跟踪构成线的坐标对,就不可能确定形状的外部边界。
如果你知道构成线的坐标对,那么
- 创建两个列表,一个顶点(列表1),一行(列表2)
- 从顶点列表中删除所有重复顶点
- 创建一个新列表(列表3),列出所有有3行行的顶点。
- 使用列表3,从列表3中删除所有有两个顶点的行作为它们的两个坐标对。
- 现在是遍历形状的时候了,剩下的行列表应该形成您想要的形状,从任意坐标开始,然后对于所有线的每个坐标,如果(x1,y1) =当前坐标,然后添加(x2,y2)来堆栈,然后从列表断点(x2,y2) =当前坐标中移除这条线,然后添加(x1,y1)到堆栈,然后从列表中断中删除这一行。
Stack Overflow用户
发布于 2012-12-01 18:28:45
对于每一个十六进制,你有一个6个顶点的列表。如果有必要,对列表进行排序,以便按逆时针顺序排列顶点(这是数学惯例)。
现在你有了一组多边形(最初是六边形)。这个想法是组合多边形,直到只有一个(或尽可能少)。
选择多边形的一条边,并在其他多边形中寻找相同的边(即同一对顶点)。如果有两个实例,则将该边的两个多边形组合起来,例如(a,b,c,d,e,f) + (g,h,d,c,i,j) => (a,b,c,i,j,g,g,h,d,e,f)。(如果两个顶点在两个多边形中的顺序相同,或者如果存在三个或多个边缘实例,则报告一个错误并终止。)遍历所有的边缘。如果这些六边形真的形成了一个连续的群,就只剩下一个多边形了。
多边形可能有重复的边。如果一个边不止出现一次,则通过将列表分成两部分来消除它,例如(a,b,c,d,b,a,e,f,g) => (b,c,d) + (a,e,f,g)。如果边缘相邻,则移除它们:(a,b,c,b,d,e) => (a,b,d,e)。或者,如果该列表只有该边,则删除该列表:(a,b) => nothing。
一旦你消除了重复的边缘,将有一个列表的逆时针外边的多边形,也许一个或多个列表顺时针方向的内部边缘的孔。
https://stackoverflow.com/questions/13664642
复制







