Hands on Reinforcement Learning Advanced Chapter
Hands on Reinforcement Learning Advanced Chapter
一只野生彩色铅笔
发布于 2023-04-24 09:51:12
发布于 2023-04-24 09:51:12
7 DQN 算法
7.1 简介
在第 5 章讲解的 Q-learning 算法中,我们以矩阵的方式建立了一张存储每个状态下所有动作值的表格。表格中的每一个动作价值Q(s,a)Q(s,a)Q(s,a)表示在状态sss下选择动作aaa然后继续遵循某一策略预期能够得到的期望回报。然而,这种用表格存储动作价值的做法只在环境的状态和动作都是离散的,并且空间都比较小的情况下适用,我们之前进行代码实战的几个环境都是如此(如悬崖漫步)。当状态或者动作数量非常大的时候,这种做法就不适用了。例如,当状态是一张 RGB 图像时,假设图像大小是210×160×3210\times 160\times 3210×160×3,此时一共有256(210×160×3)256^{(210\times 160\times 3)}256(210×160×3)种状态,在计算机中存储这个数量级的QQQ值表格是不现实的。更甚者,当状态或者动作连续的时候,就有无限个状态动作对,我们更加无法使用这种表格形式来记录各个状态动作对的QQQ值。
对于这种情况,我们需要用函数拟合的方法来估计QQQ值,即将这个复杂的QQQ值表格视作数据,使用一个参数化的函数QθQ_\thetaQθ来拟合这些数据。很显然,这种函数拟合的方法存在一定的精度损失,因此被称为近似方法。我们今天要介绍的 DQN 算法便可以用来解决连续状态下离散动作的问题。
7.2 CartPole 环境
以图 7-1 中所示的所示的车杆(CartPole)环境为例,它的状态值就是连续的,动作值是离散的。
图 7-1 CartPole环境示意图
在车杆环境中,有一辆小车,智能体的任务是通过左右移动保持车上的杆竖直,若杆的倾斜度数过大,或者车子离初始位置左右的偏离程度过大,或者坚持时间到达 200 帧,则游戏结束。智能体的状态是一个维数为 4 的向量,每一维都是连续的,其动作是离散的,动作空间大小为 2,详情参见表 7-1 和表 7-2。在游戏中每坚持一帧,智能体能获得分数为 1 的奖励,坚持时间越长,则最后的分数越高,坚持 200 帧即可获得最高的分数。
表 7-1 CartPole环境的状态空间
维度 | 意义 | 最小值 | 最大值 |
|---|---|---|---|
0 | 车的位置 | -2.4 | 2.4 |
1 | 车的速度 | -Inf | Inf |
2 | 杆的角度 | ~ -41.8° | ~ 41.8° |
3 | 杆尖端的速度 | -Inf | Inf |
表7-2 CartPole环境的动作空间
标号 | 动作 |
|---|---|
0 | 向左移动小车 |
1 | 向右移动小车 |
7.3 DQN
现在我们想在类似车杆的环境中得到动作价值函数Q(s,a)Q(s,a)Q(s,a),由于状态每一维度的值都是连续的,无法使用表格记录,因此一个常见的解决方法便是使用函数拟合(function approximation)的思想。由于神经网络具有强大的表达能力,因此我们可以用一个神经网络来表示函数QQQ。若动作是连续(无限)的,神经网络的输入是状态sss和动作aaa,然后输出一个标量,表示在状态sss下采取动作aaa能获得的价值。若动作是离散(有限)的,除了可以采取动作连续情况下的做法,我们还可以只将状态sss输入到神经网络中,使其同时输出每一个动作的QQQ值。通常 DQN(以及 Q-learning)只能处理动作离散的情况,因为在函数QQQ的更新过程中有maxa\max_amaxa这一操作。假设神经网络用来拟合函数的参数是ω\omegaω ,即每一个状态sss下所有可能动作aaa的值我们都能表示为Qω(s,a)Q_\omega(s,a)Qω(s,a)。我们将用于拟合函数QQQ函数的神经网络称为Q 网络,如图 7-2 所示。
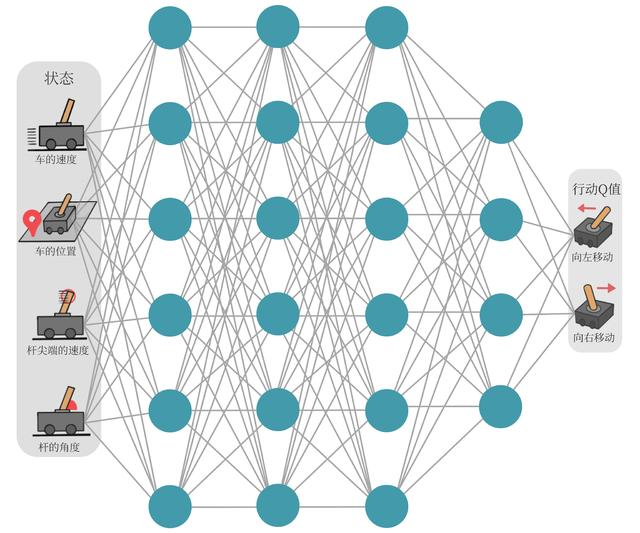
图7-2 工作在CartPole环境中的Q网络示意图
那么 Q 网络的损失函数是什么呢?我们先来回顾一下 Q-learning 的更新规则(参见 5.5 节):
Q(s,a)←Q(s,a)+α[r+γmaxa′∈AQ(s′,a′)−Q(s,a)]Q(s,a) \leftarrow Q(s,a) + \alpha \Big[ r + \gamma \max_{a'\in\mathcal{A}} Q(s',a') - Q(s,a) \Big] Q(s,a)←Q(s,a)+α[r+γa′∈AmaxQ(s′,a′)−Q(s,a)]
上述公式用时序差分(temporal difference,TD)学习目标r+γmaxa′∈AQ(s′,a′)r + \gamma \max_{a'\in\mathcal{A}} Q(s',a')r+γmaxa′∈AQ(s′,a′)来增量式更新Q(s,a)Q(s,a)Q(s,a),也就是说要使Q(s,a)Q(s,a)Q(s,a)和TD目标r+γmaxa′∈AQ(s′,a′)r + \gamma \max_{a'\in\mathcal{A}} Q(s',a')r+γmaxa′∈AQ(s′,a′)靠近。于是,对于一组数据{(si,ai,ri,si′)}\Big\{(s_i,a_i,r_i,s_i')\Big\}{(si,ai,ri,si′)},我们可以很自然地将 Q 网络的损失函数构造为均方误差的形式:
ω∗=arg minω12N∑i=1N[Qω(si,ai)−(ri+γmaxa′Qω(si′,a′))]2\omega^* = \underset{\omega}{\argmin} \dfrac{1}{2N} \sum_{i=1}^N \bigg[ Q_\omega(s_i,a_i) - \Big( r_i + \gamma \max_{a'}Q_\omega (s_i', a') \Big) \bigg]^2 ω∗=ωargmin2N1i=1∑N[Qω(si,ai)−(ri+γa′maxQω(si′,a′))]2
至此,我们就可以将 Q-learning 扩展到神经网络形式——深度 Q 网络(deep Q network,DQN)算法。由于 DQN 是离线策略算法,因此我们在收集数据的时候可以使用一个ε-贪婪策略来平衡探索与利用,将收集到的数据存储起来,在后续的训练中使用。DQN 中还有两个非常重要的模块——经验回放和目标网络,它们能够帮助 DQN 取得稳定、出色的性能。
7.3.1 经验回放
在一般的有监督学习中,假设训练数据是独立同分布的,我们每次训练神经网络的时候从训练数据中随机采样一个或若干个数据来进行梯度下降,随着学习的不断进行,每一个训练数据会被使用多次。在原来的 Q-learning 算法中,每一个数据只会用来更新一次QQQ值。为了更好地将 Q-learning 和深度神经网络结合,DQN 算法采用了经验回放(experience replay)方法,具体做法为维护一个回放缓冲区,将每次从环境中采样得到的四元组数据(状态、动作、奖励、下一状态)存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。这么做可以起到以下两个作用。
- 使样本满足独立假设。在 MDP 中交互采样得到的数据本身不满足独立假设,因为这一时刻的状态和上一时刻的状态有关。非独立同分布的数据对训练神经网络有很大的影响,会使神经网络拟合到最近训练的数据上。采用经验回放可以打破样本之间的相关性,让其满足独立假设。 如果直接使用连续的样本进行训练,会导致样本之间的相关性较强,这可能会影响训练效果,使得Q值函数收敛较慢甚至不收敛。为了避免这种情况,DQN使用经验回放机制,将智能体的经验存储在回放缓冲区中,并从中随机抽取样本进行训练。在回放缓冲区中,每个样本都是从智能体在环境中的不同时间步采集的,因此它们之间的相关性很低。通过随机抽取样本进行训练,可以保证每个样本都有相同的机会被选中,从而使得样本之间的相关性更加随机化。此外,经验回放还可以减少训练数据的相关性,从而避免了过拟合的风险。这是因为经验回放可以从回放缓冲区中删除旧的样本,同时添加新的样本,从而确保样本之间的相关性始终保持在一个合理的范围内。
- 提高样本效率。每一个样本可以被使用多次,十分适合深度神经网络的梯度学习。
7.3.2 目标网络
DQN 算法最终更新的目标是让Qω(s,a)Q_\omega(s,a)Qω(s,a)逼近r+γmaxa′Qω(s′,a′)r + \gamma \max_{a'}Q_\omega(s',a')r+γmaxa′Qω(s′,a′),由于 TD 误差目标本身就包含神经网络的输出,因此在更新网络参数的同时目标也在不断地改变,这非常容易造成神经网络训练的不稳定性(在监督学习里,标签是固定不动的,但这里的估计Q值和目标Q值会一起变动,我们希望至少有一方变动不那么大,来保证算法稳定)。为了解决这一问题,DQN 便使用了目标网络(target network)的思想:既然训练过程中 Q 网络的不断更新会导致目标不断发生改变,不如暂时先将 TD 目标中的 Q 网络固定住。为了实现这一思想,我们需要利用两套 Q 网络。
- 原来的训练网络Qω(s,a)Q_\omega(s,a)Qω(s,a),用于计算原来的损失函数12[Qω(s,a)−(r+γmaxa′Qω−(s′,a′))]2\dfrac{1}{2}\bigg[Q_\omega(s,a) - \Big(r + \gamma\underset{a'}{\max} Q_{\omega^{-}}(s',a')\Big)\bigg]^221[Qω(s,a)−(r+γa′maxQω−(s′,a′))]2中的Qω(s,a)Q_\omega(s,a)Qω(s,a)项,并且使用正常梯度下降方法来进行更新。
- 目标网络Qω−(s,a)Q_{\omega^{-}}(s,a)Qω−(s,a),用于计算原先损失函数12[Qω(s,a)−(r+γmaxa′Qω−(s′,a′))]2\dfrac{1}{2}\bigg[Q_\omega(s,a) - \Big(r + \gamma\underset{a'}{\max} Q_{\omega^{-}}(s',a')\Big)\bigg]^221[Qω(s,a)−(r+γa′maxQω−(s′,a′))]2中的(r+γmaxa′Qω−(s′,a′))\Big(r + \gamma\underset{a'}{\max} Q_{\omega^{-}}(s',a')\Big)(r+γa′maxQω−(s′,a′))项,其中ω−\omega^{-}ω−表示目标网络中的参数。如果两套网络的参数随时保持一致,则仍为原先不够稳定的算法。为了让更新目标更稳定,目标网络并不会每一步都更新。具体而言,目标网络使用训练网络的一套较旧的参数,训练网络Qω(s,a)Q_\omega(s,a)Qω(s,a)在训练中的每一步都会更新,而目标网络的参数每隔CCC步才会与训练网络同步一次,即ω−←ω\omega^{-} \leftarrow \omegaω−←ω。这样做使得目标网络相对于训练网络更加稳定。
综上所述,DQN 算法的具体流程如下:
- 用随机的网络参数ω\omegaω初始化网络Qω(s,a)Q_\omega(s,a)Qω(s,a)
- 复制相同的参数ω−←ω\omega^{-}\leftarrow \omegaω−←ω来初始化目标网络Qω−Q_{\omega^{-}}Qω−
- 初始化经验回放池RRR
- for 序列e=1→Ee=1\rightarrow Ee=1→E do
- 获取环境初始状态s1s_1s1
- for 时间步t=1→Tt=1\rightarrow Tt=1→T do
- 根据当前网络Qω(s,a)Q_\omega(s,a)Qω(s,a)以ε-贪婪策略选择动作ata_tat
- 执行动作ata_tat,获得回报rtr_trt,环境状态变为st+1s_{t+1}st+1
- 将(st,at,rt,st+1)(s_t,a_t,r_t,s_{t+1})(st,at,rt,st+1)存储进回放池RRR中
- 若RRR中数据足够,从RRR中采样NNN个数据{(s1,ai,ri,si+1)}i=1,…,N\Big\{(s_1,a_i,r_i,s_{i+1})\Big\}_{i=1,\dots,N}{(s1,ai,ri,si+1)}i=1,…,N
- 对每个数据,用目标网络计算yi=ri+γmaxaQω−(si+1,a)y_i=r_i+\gamma\max_aQ_{\omega^{-}}(s_{i+1},a)yi=ri+γmaxaQω−(si+1,a)
- 最小化目标损失L=1N∑i12(yi−Qω(si,ai))2L=\dfrac{1}{N}\underset{i}{\sum}\dfrac{1}{2}\Big(y_i - Q_\omega(s_i,a_i)\Big)^2L=N1i∑21(yi−Qω(si,ai))2,以此更新当前网络QωQ_\omegaQω
- 更新目标网络
- end for
- end for
7.4 DQN 代码实践
接下来,我们就正式进入 DQN 算法的代码实践环节。我们采用的测试环境是 CartPole-v0,其状态空间相对简单,只有 4 个变量,因此网络结构的设计也相对简单:采用一层 128 个神经元的全连接并以 ReLU 作为激活函数。当遇到更复杂的诸如以图像作为输入的环境时,我们可以考虑采用深度卷积神经网络。
从 DQN 算法开始,我们将会用到rl_utils库,它包含一些专门为本书准备的函数,如绘制移动平均曲线、计算优势函数等,不同的算法可以一起使用这些函数。为了能够调用rl_utils库,请从本书的GitHub 仓库下载rl_utils.py文件。
import random
import gym
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
首先定义经验回放池的类,主要包括加入数据、采样数据两大函数。
class ReplayBuffer:
''' 经验回放池 '''
def __init__(self, capacity):
self.buffer = collections.deque(maxlen=capacity) # 队列,先进先出
def add(self, state, action, reward, next_state, done): # 将数据加入buffer
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size): # 从buffer中采样数据,数量为batch_size
transitions = random.sample(self.buffer, batch_size)
state, action, reward, next_state, done = zip(*transitions)
return np.array(state), action, reward, np.array(next_state), done
def size(self): # 目前buffer中数据的数量
return len(self.buffer)
然后定义一个只有一层隐藏层的 Q 网络。
class Qnet(torch.nn.Module):
''' 只有一层隐藏层的Q网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(Qnet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x)) # 隐藏层使用ReLU激活函数
return self.fc2(x)
有了这些基本组件之后,接来下开始实现 DQN 算法。
class DQN:
''' DQN算法 '''
def __init__(self,
state_dim,
hidden_dim,
action_dim,
learning_rate,
gamma,
epsilon,
target_update,
device
):
self.action_dim = action_dim
self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device) # Q网络
# 目标网络
self.target_q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
# 使用Adam优化器
self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略
self.target_update = target_update # 目标网络更新频率
self.count = 0 # 计数器,记录更新次数
self.device = device
def take_action(self, state): # epsilon-贪婪策略采取动作
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q值
# 下个状态的最大Q值
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # TD误差目标
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
dqn_loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(self.q_net.state_dict()) # 更新目标网络
self.count += 1
一切准备就绪,开始训练并查看结果。我们之后会将这一训练过程包装进rl_utils库中,方便之后要学习的算法的代码实现。
lr = 2e-3
num_episodes = 500
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 10
buffer_size = 10000
minimal_size = 500
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device)
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done, _ = env.step(action)
replay_buffer.add(state, action, reward, next_state, done)
state = next_state
episode_return += reward
# 当buffer数据的数量超过一定值后,才进行Q网络训练
if replay_buffer.size() > minimal_size:
b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
transition_dict = {
'states': b_s,
'actions': b_a,
'next_states': b_ns,
'rewards': b_r,
'dones': b_d
}
agent.update(transition_dict)
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
Iteration 0: 100%|████████████████████████████████████████| 50/50 [00:00<00:00, 589.55it/s, episode=50, return=9.300]
Iteration 1: 100%|████████████████████████████████████████| 50/50 [00:00<00:00, 60.01it/s, episode=100, return=12.300]
Iteration 2: 100%|████████████████████████████████████████| 50/50 [00:04<00:00, 11.94it/s, episode=150, return=123.000]
Iteration 3: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.27it/s, episode=200, return=159.300]
Iteration 4: 100%|████████████████████████████████████████| 50/50 [00:16<00:00, 3.04it/s, episode=250, return=192.200]
Iteration 5: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.23it/s, episode=300, return=199.900]
Iteration 6: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.28it/s, episode=350, return=193.400]
Iteration 7: 100%|████████████████████████████████████████| 50/50 [00:16<00:00, 3.10it/s, episode=400, return=200.000]
Iteration 8: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.28it/s, episode=450, return=172.300]
Iteration 9: 100%|████████████████████████████████████████| 50/50 [00:15<00:00, 3.32it/s, episode=500, return=185.000]
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()
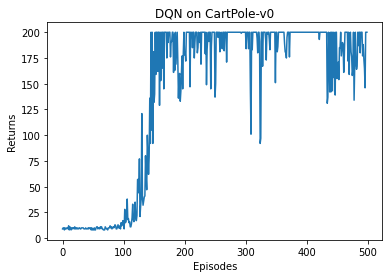
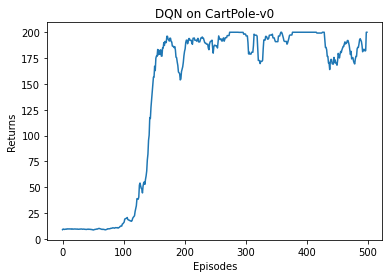
可以看到,DQN 的性能在 100 个序列后很快得到提升,最终收敛到策略的最优回报值 200。我们也可以看到,在 DQN 的性能得到提升后,它会持续出现一定程度的震荡,这主要是神经网络过拟合到一些局部经验数据后由arg max\argmaxargmax运算带来的影响。
7.5 以图像为输入的 DQN 算法
在本书前面章节所述的强化学习环境中,我们都使用非图像的状态作为输入(例如车杆环境中车的坐标、速度),但是在一些视频游戏中,智能体并不能直接获取这些状态信息,而只能直接获取屏幕中的图像。要让智能体和人一样玩游戏,我们需要让智能体学会以图像作为状态时的决策。我们可以利用 7.4 节的 DQN 算法,将卷积层加入其网络结构以提取图像特征,最终实现以图像为输入的强化学习。以图像为输入的 DQN 算法的代码与 7.4 节的代码的不同之处主要在于 Q 网络的结构和数据输入。DQN 网络通常会将最近的几帧图像一起作为输入,从而感知环境的动态性。接下来我们实现以图像为输入的 DQN 算法,但由于代码需要运行较长的时间,我们在此便不展示训练结果。
class ConvolutionalQnet(torch.nn.Module):
''' 加入卷积层的Q网络 '''
def __init__(self, action_dim, in_channels=4):
super(ConvolutionalQnet, self).__init__()
self.conv1 = torch.nn.Conv2d(in_channels, 32, kernel_size=8, stride=4)
self.conv2 = torch.nn.Conv2d(32, 64, kernel_size=4, stride=2)
self.conv3 = torch.nn.Conv2d(64, 64, kernel_size=3, stride=1)
self.fc4 = torch.nn.Linear(7 * 7 * 64, 512)
self.head = torch.nn.Linear(512, action_dim)
def forward(self, x):
x = x / 255
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
x = F.relu(self.conv3(x))
x = F.relu(self.fc4(x))
return self.head(x)
7.6 小结
本章讲解了 DQN 算法,其主要思想是用一个神经网络来表示最优策略的函数QQQ,然后利用 Q-learning 的思想进行参数更新。为了保证训练的稳定性和高效性,DQN 算法引入了经验回放和目标网络两大模块,使得算法在实际应用时能够取得更好的效果。在 2013 年的 NIPS 深度学习研讨会上,DeepMind 公司的研究团队发表了 DQN 论文,首次展示了这一直接通过卷积神经网络接受像素输入来玩转各种雅达利(Atari)游戏的强化学习算法,由此拉开了深度强化学习的序幕。DQN 是深度强化学习的基础,掌握了该算法才算是真正进入了深度强化学习领域,本书中还有更多的深度强化学习算法等待读者探索。
7.7 参考文献
[1] VOLODYMYR M, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning [J]. Nature, 2015, 518(7540): 529-533.
[2] VOLODYMYR M, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning [C]//NIPS Deep Learning Workshop, 2013.
8 DQN 改进算法
8.1 简介
DQN 算法敲开了深度强化学习的大门,但是作为先驱性的工作,其本身存在着一些问题以及一些可以改进的地方。于是,在 DQN 之后,学术界涌现出了非常多的改进算法。本章将介绍其中两个非常著名的算法:Double DQN 和 Dueling DQN,这两个算法的实现非常简单,只需要在 DQN 的基础上稍加修改,它们能在一定程度上改善 DQN 的效果。如果读者想要了解更多、更详细的 DQN 改进方法,可以阅读 Rainbow 模型的论文及其引用文献。
8.2 Double DQN
普通的 DQN 算法通常会导致对QQQ值的过高估计(overestimation)。传统 DQN 优化的 TD 误差目标为
r+γmaxa′Qω−(s′,a′)r + \gamma \max_{a'} Q_{\omega^{-}}(s',a') r+γa′maxQω−(s′,a′)
其中maxa′Qω−(s′,a′)\max_a' Q_{\omega^{-}}(s',a')maxa′Qω−(s′,a′)由目标网络(参数为ω−\omega^{-}ω−)计算得出,我们还可以将其写成如下形式:
Qω−(s′,arg maxa′Qω−(s′,a′))Q_{\omega^{-}} \Big( s', \underset{a'}{\argmax} Q_{\omega^{-}}(s',a') \Big) Qω−(s′,a′argmaxQω−(s′,a′))
换句话说,max\maxmax操作实际可以被拆解为两部分:首先选取状态s′s's′下的最优动作a∗=arg maxa′Qω−(s′,a′)a^*=\underset{a'}{\argmax} Q_{\omega^{-}}(s',a')a∗=a′argmaxQω−(s′,a′),接着计算该动作对应的价值Qω−(s′,a∗)Q_{\omega^{-}}(s',a^{*})Qω−(s′,a∗)。 当这两部分采用同一套 Q 网络进行计算时,每次得到的都是神经网络当前估算的所有动作价值中的最大值。考虑到通过神经网络估算的QQQ值本身在某些时候会产生正向或负向的误差,在 DQN 的更新方式下神经网络会将正向误差累积。例如,我们考虑一个特殊情形:在状态s′s's′下所有动作QQQ的值均为 000,即Q(s′,ai)=0,∀iQ(s',a_i)=0,\forall iQ(s′,ai)=0,∀i,此时正确的更新目标应为r+0=rr+0=rr+0=r,但是由于神经网络拟合的误差通常会出现某些动作的估算有正误差的情况,即存在某个动作a′a'a′有Q(s′,a′)>0Q(s',a')>0Q(s′,a′)>0,此时我们的更新目标出现了过高估计,r+γmaxQ>r+0r+\gamma\max Q > r + 0r+γmaxQ>r+0。因此,当我们用 DQN 的更新公式进行更新时,Q(s,a)Q(s,a)Q(s,a)也就会被过高估计了。同理,我们拿这个Q(s,a)Q(s,a)Q(s,a)来作为更新目标来更新上一步的QQQ值时,同样会过高估计,这样的误差将会逐步累积。对于动作空间较大的任务,DQN 中的过高估计问题会非常严重,造成 DQN 无法有效工作的后果。
为了解决这一问题,Double DQN 算法提出利用两个独立训练的神经网络估算maxa′Q∗(s′,a′)\max\limits_{a'}Q_{*}(s',a')a′maxQ∗(s′,a′)。具体做法是将原有的maxa′Qω−(s′,a′)\max\limits_{a'}Q_{\omega^{-}}(s',a')a′maxQω−(s′,a′)更改为Qω−(s′,arg maxa′Qω(s′,a′))Q_{\omega^{-}}(s',\underset{a'}{\argmax}Q_{\omega}(s',a'))Qω−(s′,a′argmaxQω(s′,a′)),即利用一套神经网络QωQ_\omegaQω的输出选取价值最大的动作,但在使用该动作的价值时,用另一套神经网络Qω−Q_\omega^-Qω−计算该动作的价值。这样,即使其中一套神经网络的某个动作存在比较严重的过高估计问题,由于另一套神经网络的存在,这个动作最终使用的QQQ值不会存在很大的过高估计问题。
在传统的 DQN 算法中,本来就存在两套QQQ函数的神经网络——目标网络和训练网络(参见 7.3.2 节),只不过maxa′Qω−(s′,a′)\underset{a'}{\max}Q_{\omega^{-}}(s',a')a′maxQω−(s′,a′)的计算只用到了其中的目标网络,那么我们恰好可以直接将训练网络作为 Double DQN 算法中的第一套神经网络来选取动作,将目标网络作为第二套神经网络计算QQQ值,这便是 Double DQN 的主要思想。由于在 DQN 算法中将训练网络的参数记为ω\omegaω,将目标网络的参数记为ω−\omega^{-}ω−,这与本节中 Double DQN 的两套神经网络的参数是统一的,因此,我们可以直接写出如下 Double DQN 的优化目标:
r+γQω−(s′,arg maxa′Qω(s′,a′))r + \gamma Q_{\omega^{-}} \Big( s', \underset{a'}{\argmax}Q_{\omega}(s',a') \Big) r+γQω−(s′,a′argmaxQω(s′,a′))
8.3 Double DQN 代码实践
显然,DQN 与 Double DQN 的差别只是在于计算状态s′s's′下QQQ值时如何选取动作:
- DQN 的优化目标可以写为r+γQω−(s′,arg maxa′Qω−(s′,a′))r + \gamma Q_{\omega^{-}}(s',\underset{a'}{\argmax} Q_{\omega^{-}}(s', a'))r+γQω−(s′,a′argmaxQω−(s′,a′)),动作的选取依靠目标网络Qω−Q_{\omega^{-}}Qω−;
- Double DQN 的优化目标为r+γQω−(s′,arg maxa′Qω(s′,a′))r + \gamma Q_{\omega^{-}}(s',\underset{a'}{\argmax} Q_{\omega}(s', a'))r+γQω−(s′,a′argmaxQω(s′,a′)),动作的选取依靠训练网络QωQ_{\omega}Qω。
所以 Double DQN 的代码实现可以直接在 DQN 的基础上进行,无须做过多修改。
本节采用的环境是倒立摆(Inverted Pendulum),该环境下有一个处于随机位置的倒立摆,如图 8-1 所示。环境的状态包括倒立摆角度的正弦值sinθ\sin\thetasinθ,余弦值cosθ\cos\thetacosθ,角速度θ˙\dot\thetaθ˙;动作为对倒立摆施加的力矩,详情参见表 8-1 和表 8-2。每一步都会根据当前倒立摆的状态的好坏给予智能体不同的奖励,该环境的奖励函数为−(θ2+0.1θ˙2+0.001a2)-(\theta^2 + 0.1\dot\theta^2 + 0.001a^2)−(θ2+0.1θ˙2+0.001a2),倒立摆向上保持直立不动时奖励为 000,倒立摆在其他位置时奖励为负数。环境本身没有终止状态,运行 200200200 步后游戏自动结束。
图8-1 Pendulum环境示意图
标号 | 名称 | 最小值 | 最大值 |
|---|---|---|---|
0 | cosθ\cos\thetacosθ | -1.0 | 1.0 |
1 | sinθ\sin\thetasinθ | -1.0 | 1.0 |
2 | θ˙\dot\thetaθ˙ | -8.0 | 8.0 |
表8-1 Pendulum环境的状态空间
标号 | 动作 | 最小值 | 最大值 |
|---|---|---|---|
0 | 力矩 | -2.0 | 2.0 |
表8-2 Pendulum环境的动作空间
力矩大小是在[−2,2][-2, 2][−2,2]范围内的连续值。由于 DQN 只能处理离散动作环境,因此我们无法直接用 DQN 来处理倒立摆环境,但倒立摆环境可以比较方便地验证 DQN 对QQQ值的过高估计:倒立摆环境下QQQ值的最大估计应为 000(倒立摆向上保持直立时能选取的最大QQQ值),值出现大于 000 的情况则说明出现了过高估计。为了能够应用 DQN,我们采用离散化动作的技巧。例如,下面的代码将连续的动作空间离散为 111111 个动作。动作[0,1,2,⋯ ,9,10][0,1,2,\cdots,9,10][0,1,2,⋯,9,10]分别代表力矩为[−2,−1.6,−1.2,⋯ ,1.2,1.6,2][-2, -1.6,-1.2,\cdots,1.2, 1.6, 2][−2,−1.6,−1.2,⋯,1.2,1.6,2]。
import random
import gym
import numpy as np
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
from tqdm import tqdm
class Qnet(torch.nn.Module):
''' 只有一层隐藏层的Q网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(Qnet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
接下来我们在 DQN 代码的基础上稍做修改以实现 Double DQN。
class DQN:
''' DQN算法,包括Double DQN '''
def __init__(self,
state_dim,
hidden_dim,
action_dim,
learning_rate,
gamma,
epsilon,
target_update,
device,
dqn_type='VanillaDQN'):
self.action_dim = action_dim
self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
self.target_q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
self.gamma = gamma
self.epsilon = epsilon
self.target_update = target_update
self.count = 0
self.dqn_type = dqn_type
self.device = device
def take_action(self, state):
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def max_q_value(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
return self.q_net(state).max().item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q值
# 下个状态的最大Q值
if self.dqn_type == 'DoubleDQN': # DQN与Double DQN的区别
max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
else: # DQN的情况
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # TD误差目标
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
dqn_loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(self.q_net.state_dict()) # 更新目标网络
self.count += 1
接下来我们设置相应的超参数,并实现将倒立摆环境中的连续动作转化为离散动作的函数。
lr = 1e-2
num_episodes = 200
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 50
buffer_size = 5000
minimal_size = 1000
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'Pendulum-v0'
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = 11 # 将连续动作分成11个离散动作
def dis_to_con(discrete_action, env, action_dim): # 离散动作转回连续的函数
action_lowbound = env.action_space.low[0] # 连续动作的最小值
action_upbound = env.action_space.high[0] # 连续动作的最大值
return action_lowbound + (discrete_action / (action_dim - 1)) * (action_upbound - action_lowbound)
接下来要对比 DQN 和 Double DQN 的训练情况,为了便于后续多次调用,我们进一步将 DQN 算法的训练过程定义成一个函数。训练过程会记录下每个状态的最大值,在训练完成后我们可以将结果可视化,观测这些QQQ值存在的过高估计的情况,以此来对比 DQN 和 Double DQN 的不同。
def train_DQN(agent, env, num_episodes, replay_buffer, minimal_size, batch_size):
return_list = []
max_q_value_list = []
max_q_value = 0
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
max_q_value = agent.max_q_value(state) * 0.005 + max_q_value * 0.995 # 平滑处理
max_q_value_list.append(max_q_value) # 保存每个状态的最大Q值
action_continuous = dis_to_con(action, env, agent.action_dim)
next_state, reward, done, _ = env.step([action_continuous])
replay_buffer.add(state, action, reward, next_state, done)
state = next_state
episode_return += reward
if replay_buffer.size() > minimal_size:
b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
transition_dict = {
'states': b_s,
'actions': b_a,
'next_states': b_ns,
'rewards': b_r,
'dones': b_d
}
agent.update(transition_dict)
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
return return_list, max_q_value_list
一切就绪!我们首先训练 DQN 并打印出其学习过程中最大QQQ值的情况。
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device)
return_list, max_q_value_list = train_DQN(agent, env, num_episodes, replay_buffer, minimal_size, batch_size)
episodes_list = list(range(len(return_list)))
mv_return = rl_utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()
frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('DQN on {}'.format(env_name))
plt.show()
Iteration 0: 100%|██████████| 20/20 [00:02<00:00, 7.14it/s, episode=20, return=-1018.764]
Iteration 1: 100%|██████████| 20/20 [00:03<00:00, 5.73it/s, episode=40, return=-463.311]
Iteration 2: 100%|██████████| 20/20 [00:03<00:00, 5.53it/s, episode=60, return=-184.817]
Iteration 3: 100%|██████████| 20/20 [00:03<00:00, 5.55it/s, episode=80, return=-317.366]
Iteration 4: 100%|██████████| 20/20 [00:03<00:00, 5.67it/s, episode=100, return=-208.929]
Iteration 5: 100%|██████████| 20/20 [00:03<00:00, 5.59it/s, episode=120, return=-182.659]
Iteration 6: 100%|██████████| 20/20 [00:03<00:00, 5.25it/s, episode=140, return=-275.938]
Iteration 7: 100%|██████████| 20/20 [00:03<00:00, 5.65it/s, episode=160, return=-209.702]
Iteration 8: 100%|██████████| 20/20 [00:03<00:00, 5.73it/s, episode=180, return=-246.861]
Iteration 9: 100%|██████████| 20/20 [00:03<00:00, 5.77it/s, episode=200, return=-293.374]
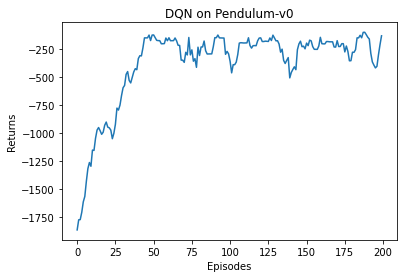
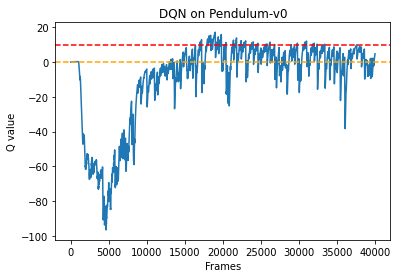
根据代码运行结果我们可以发现,DQN 算法在倒立摆环境中能取得不错的回报,最后的期望回报在−200-200−200左右,但是不少QQQ值超过了 000,有一些还超过了 101010,该现象便是 DQN 算法中的QQQ值过高估计。我们现在来看一下 Double DQN 是否能对此问题进行改善。
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device, 'DoubleDQN')
return_list, max_q_value_list = train_DQN(agent, env, num_episodes, replay_buffer, minimal_size, batch_size)
episodes_list = list(range(len(return_list)))
mv_return = rl_utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Double DQN on {}'.format(env_name))
plt.show()
frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('Double DQN on {}'.format(env_name))
plt.show()
Iteration 0: 100%|██████████| 20/20 [00:03<00:00, 6.60it/s, episode=20, return=-818.719]
Iteration 1: 100%|██████████| 20/20 [00:03<00:00, 5.43it/s, episode=40, return=-391.392]
Iteration 2: 100%|██████████| 20/20 [00:03<00:00, 5.29it/s, episode=60, return=-216.078]
Iteration 3: 100%|██████████| 20/20 [00:03<00:00, 5.52it/s, episode=80, return=-438.220]
Iteration 4: 100%|██████████| 20/20 [00:03<00:00, 5.42it/s, episode=100, return=-162.128]
Iteration 5: 100%|██████████| 20/20 [00:03<00:00, 5.50it/s, episode=120, return=-389.088]
Iteration 6: 100%|██████████| 20/20 [00:03<00:00, 5.44it/s, episode=140, return=-273.700]
Iteration 7: 100%|██████████| 20/20 [00:03<00:00, 5.23it/s, episode=160, return=-221.605]
Iteration 8: 100%|██████████| 20/20 [00:04<00:00, 4.91it/s, episode=180, return=-262.134]
Iteration 9: 100%|██████████| 20/20 [00:03<00:00, 5.34it/s, episode=200, return=-278.752]
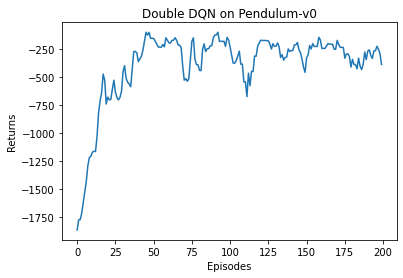
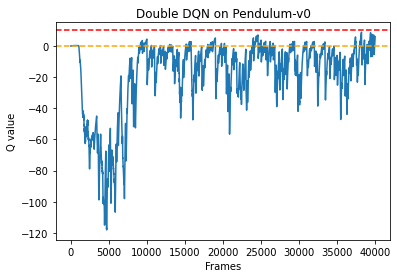
我们可以发现,与普通的 DQN 相比,Double DQN 比较少出现QQQ值大于 000 的情况,说明QQQ值过高估计的问题得到了很大缓解。
8.4 Dueling DQN
Dueling DQN 是 DQN 另一种的改进算法,它在传统 DQN 的基础上只进行了微小的改动,但却能大幅提升 DQN 的表现。在强化学习中,我们将状态动作价值函数QQQ减去状态价值函数VVV的结果定义为优势函数AAA,即A(s,a)=Q(s,a)−V(s)A(s,a) = Q(s,a) - V(s)A(s,a)=Q(s,a)−V(s)。在同一个状态下,所有动作的优势值之和为 000,因为所有动作的动作价值的期望就是这个状态的状态价值。据此,在 Dueling DQN 中,Q 网络被建模为:
Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)Q_{\eta,\alpha,\beta}(s,a) = V_{\eta,\alpha}(s) + A_{\eta,\beta}(s,a) Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)
其中,Vη,α(s)V_{\eta,\alpha}(s)Vη,α(s)为状态价值函数,而Aη,β(s,a)A_{\eta,\beta}(s,a)Aη,β(s,a)则为该状态下采取不同动作的优势函数,表示采取不同动作的差异性;η\etaη是状态价值函数和优势函数共享的网络参数,一般用在神经网络中,用来提取特征的前几层;而α\alphaα和β\betaβ分别为状态价值函数和优势函数的参数。在这样的模型下,我们不再让神经网络直接输出QQQ值,而是训练神经网络的最后几层的两个分支,分别输出状态价值函数和优势函数,再求和得到QQQ值。Dueling DQN 的网络结构如图 8-2 所示。
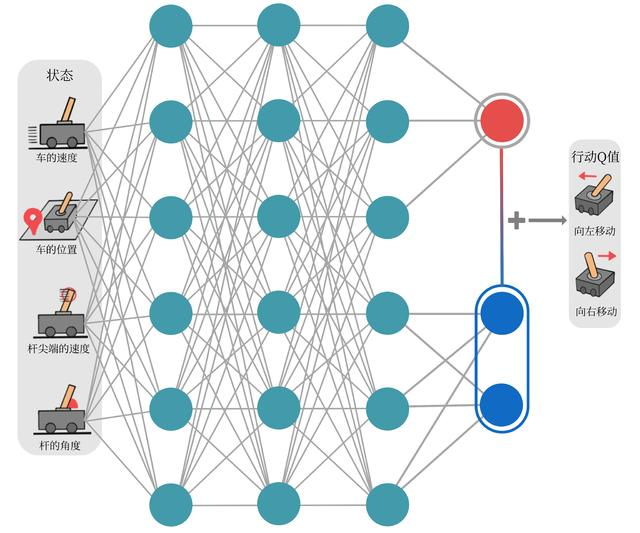
图8-2 Dueling DQN的网络结构图
将状态价值函数和优势函数分别建模的好处在于:某些情境下智能体只会关注状态的价值,而并不关心不同动作导致的差异,此时将二者分开建模能够使智能体更好地处理与动作关联较小的状态。在图 8-3 所示的驾驶车辆游戏中,智能体注意力集中的部位被显示为橙色(另见彩插图 4),当智能体前面没有车时,车辆自身动作并没有太大差异,此时智能体更关注状态价值,而当智能体前面有车时(智能体需要超车),智能体开始关注不同动作优势值的差异。
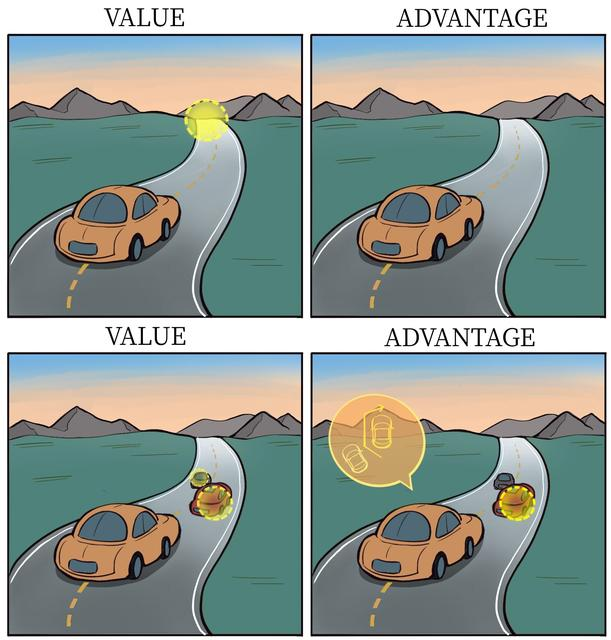
图8-3 状态价值和优势值的简单例子
对于 Dueling DQN 中的公式Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)Q_{\eta,\alpha,\beta}(s,a) = V_{\eta,\alpha}(s) + A_{\eta,\beta}(s,a)Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a),它存在对于VVV值和AAA值建模不唯一性的问题。例如,对于同样的QQQ值,如果将VVV值加上任意大小的常数CCC,再将所有AAA值减去CCC,则得到的QQQ值依然不变,这就导致了训练的不稳定性。为了解决这一问题,Dueling DQN 强制最优动作的优势函数的实际输出为 000,即:
Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)−maxa′Aη,β(s,a′)Q_{\eta,\alpha,\beta}(s,a) = V_{\eta,\alpha}(s) + A_{\eta,\beta}(s,a) - \max_{a'} A_{\eta,\beta}(s,a') Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)−a′maxAη,β(s,a′)
此时V(s)=maxaQ(s,a)V(s)=\max\limits_aQ(s,a)V(s)=amaxQ(s,a),可以确保VVV值建模的唯一性。在实现过程中,我们还可以用平均代替最大化操作,即:
Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)−1A∑a′Aη,β(s,a′)Q_{\eta,\alpha,\beta}(s,a) = V_{\eta,\alpha}(s) + A_{\eta,\beta}(s,a) - \dfrac{1}{\mathcal{A}} \sum_{a'} A_{\eta,\beta}(s,a') Qη,α,β(s,a)=Vη,α(s)+Aη,β(s,a)−A1a′∑Aη,β(s,a′)
此时V(s)=1A∑a′Q(s,a′)V(s)=\dfrac{1}{\mathcal{A}} \sum\limits_{a'} Q(s,a')V(s)=A1a′∑Q(s,a′)。在下面的代码实现中,我们将采取此种方式,虽然它不再满足贝尔曼最优方程,但实际应用时更加稳定。
有的读者可能会问:“为什么 Dueling DQN 会比 DQN 好?”部分原因在于 Dueling DQN 能更高效学习状态价值函数。每一次更新时,函数VVV都会被更新,这也会影响到其他动作的QQQ值。而传统的 DQN 只会更新某个动作的QQQ值,其他动作的QQQ值就不会更新。因此,Dueling DQN 能够更加频繁、准确地学习状态价值函数。
8.5 Dueling DQN 代码实践
Dueling DQN 与 DQN 相比的差异只是在网络结构上,大部分代码依然可以继续沿用。我们定义状态价值函数和优势函数的复合神经网络VAnet。
class VAnet(torch.nn.Module):
''' 只有一层隐藏层的A网络和V网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(VAnet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim) # 共享网络部分
self.fc_A = torch.nn.Linear(hidden_dim, action_dim)
self.fc_V = torch.nn.Linear(hidden_dim, 1)
def forward(self, x):
A = self.fc_A(F.relu(self.fc1(x)))
V = self.fc_V(F.relu(self.fc1(x)))
Q = V + A - A.mean(1).view(-1, 1) # Q值由V值和A值计算得到
return Q
class DQN:
''' DQN算法,包括Double DQN和Dueling DQN '''
def __init__(self,
state_dim,
hidden_dim,
action_dim,
learning_rate,
gamma,
epsilon,
target_update,
device,
dqn_type='VanillaDQN'):
self.action_dim = action_dim
if dqn_type == 'DuelingDQN': # Dueling DQN采取不一样的网络框架
self.q_net = VAnet(state_dim, hidden_dim,
self.action_dim).to(device)
self.target_q_net = VAnet(state_dim, hidden_dim,
self.action_dim).to(device)
else:
self.q_net = Qnet(state_dim, hidden_dim,
self.action_dim).to(device)
self.target_q_net = Qnet(state_dim, hidden_dim,
self.action_dim).to(device)
self.optimizer = torch.optim.Adam(self.q_net.parameters(),
lr=learning_rate)
self.gamma = gamma
self.epsilon = epsilon
self.target_update = target_update
self.count = 0
self.dqn_type = dqn_type
self.device = device
def take_action(self, state):
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def max_q_value(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
return self.q_net(state).max().item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions)
if self.dqn_type == 'DoubleDQN':
max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
max_next_q_values = self.target_q_net(next_states).gather(
1, max_action)
else:
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(
-1, 1)
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
self.optimizer.zero_grad()
dqn_loss.backward()
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(self.q_net.state_dict())
self.count += 1
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
target_update, device, 'DuelingDQN')
return_list, max_q_value_list = train_DQN(agent, env, num_episodes,
replay_buffer, minimal_size,
batch_size)
episodes_list = list(range(len(return_list)))
mv_return = rl_utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Dueling DQN on {}'.format(env_name))
plt.show()
frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('Dueling DQN on {}'.format(env_name))
plt.show()
Iteration 0: 100%|███████████████████████████████████████| 20/20 [00:10<00:00, 1.87it/s, episode=20, return=-708.652]
Iteration 1: 100%|███████████████████████████████████████| 20/20 [00:15<00:00, 1.28it/s, episode=40, return=-229.557]
Iteration 2: 100%|███████████████████████████████████████| 20/20 [00:15<00:00, 1.32it/s, episode=60, return=-184.607]
Iteration 3: 100%|███████████████████████████████████████| 20/20 [00:13<00:00, 1.50it/s, episode=80, return=-200.323]
Iteration 4: 100%|███████████████████████████████████████| 20/20 [00:13<00:00, 1.51it/s, episode=100, return=-213.811]
Iteration 5: 100%|███████████████████████████████████████| 20/20 [00:13<00:00, 1.53it/s, episode=120, return=-181.165]
Iteration 6: 100%|███████████████████████████████████████| 20/20 [00:14<00:00, 1.35it/s, episode=140, return=-222.040]
Iteration 7: 100%|███████████████████████████████████████| 20/20 [00:14<00:00, 1.35it/s, episode=160, return=-173.313]
Iteration 8: 100%|███████████████████████████████████████| 20/20 [00:12<00:00, 1.62it/s, episode=180, return=-236.372]
Iteration 9: 100%|███████████████████████████████████████| 20/20 [00:12<00:00, 1.57it/s, episode=200, return=-230.058]
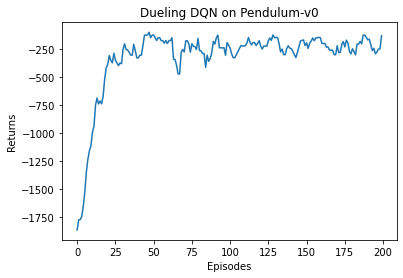
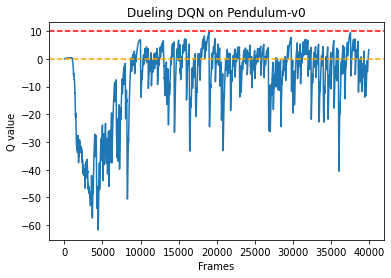
根据代码运行结果我们可以发现,相比于传统的 DQN,Dueling DQN 在多个动作选择下的学习更加稳定,得到的回报最大值也更大。由 Dueling DQN 的原理可知,随着动作空间的增大,Dueling DQN 相比于 DQN 的优势更为明显。之前我们在环境中设置的离散动作数为 11,我们可以增加离散动作数(例如 15、25 等),继续进行对比实验。
8.6 总结
在传统的 DQN 基础上,有两种非常容易实现的变式——Double DQN 和 Dueling DQN,Double DQN 解决了 DQN 中对QQQ值的过高估计,而 Dueling DQN 能够很好地学习到不同动作的差异性,在动作空间较大的环境下非常有效。从 Double DQN 和 Dueling DQN 的方法原理中,我们也能感受到深度强化学习的研究是在关注深度学习和强化学习有效结合:一是在深度学习的模块的基础上,强化学习方法如何更加有效地工作,并避免深度模型学习行为带来的一些问题,例如使用 Double DQN 解决QQQ值过高估计的问题;二是在强化学习的场景下,深度学习模型如何有效学习到有用的模式,例如设计 Dueling DQN 网络架构来高效地学习状态价值函数以及动作优势函数。
8.7 扩展阅读: 对 Q 值过高估计的定量分析
我们可以对QQQ值的过高估计做简化的定量分析。假设在状态sss下所有动作的期望回报均无差异,即Q∗(s,a)=V∗(s)Q^{*}(s,a)=V^{*}(s)Q∗(s,a)=V∗(s)(此设置是为了定量分析所简化的情形,实际上不同动作的期望回报通常会存在差异);假设神经网络估算误差Qω−(s,a)−V∗Q_{\omega^{-}}(s,a) - V^*Qω−(s,a)−V∗服从[−1,1][-1,1][−1,1]之间的均匀独立同分布;假设动作空间大小为mmm。那么,对于任意状态sss,有:
E[maxaQω−(s,a)−maxa′Q∗(s,a′)]=m−1m+1\mathbb{E} \Big[ \max_a Q_{\omega^{-}}(s,a) - \max_{a'}Q_{*}(s,a') \Big] = \dfrac{m-1}{m+1} E[amaxQω−(s,a)−a′maxQ∗(s,a′)]=m+1m−1
即动作空间mmm越大时,QQQ值过高,估计越严重。
证明:将估算误差记为ϵa=Qω−(s,a)−maxa′Q∗(s,a′)\epsilon_a = Q_{\omega^{-}}(s,a) - \max\limits_{a'}Q^{*}(s,a')ϵa=Qω−(s,a)−a′maxQ∗(s,a′),由于估算误差对于不同的动作是独立的,因此有:
P(maxaϵa≤x)=∏a=1mP(ϵa≤x)P(\max_{a} \epsilon_a \le x) = \prod_{a=1}^m P(\epsilon_a \le x) P(amaxϵa≤x)=a=1∏mP(ϵa≤x)
P(ϵa≤x)P(\epsilon_a \le x)P(ϵa≤x)是的累积分布函数(cumulative distribution function,即 CDF),它可以具体被写为:
P(ϵa≤x)={0if x≤−1x+12if x∈(−1,1)1if x≥1P(\epsilon_a \le x) = \begin{cases} 0 & \text{if } x \le -1 \\ \dfrac{x+1}{2} & \text{if } x \in (-1,1)\\ 1 & \text{if } x \ge 1 \end{cases} P(ϵa≤x)=⎩⎨⎧02x+11if x≤−1if x∈(−1,1)if x≥1
因此,我们得到关于maxaϵa\max\limits_{a} \epsilon_aamaxϵa的累积分布函数:
P(maxaϵa≤x)=∏a=1mP(ϵa≤x)={0if x≤−1(x+12)mif x∈(−1,1)1if x≥1\begin{aligned} P(\max_{a} \epsilon_a \le x) &= \prod_{a=1}^m P(\epsilon_a \le x)\\ &= \begin{cases} 0 & \text{if } x \le -1 \\ (\dfrac{x+1}{2})^m & \text{if } x \in (-1,1)\\ 1 & \text{if } x \ge 1 \end{cases} \end{aligned} P(amaxϵa≤x)=a=1∏mP(ϵa≤x)=⎩⎨⎧0(2x+1)m1if x≤−1if x∈(−1,1)if x≥1
最后我们可以得到:
E[maxaϵa]=∫−11xddxP(maxaϵa≤x)dx=[(x+12)mmx−1m+1]∣−11=m−1m+1\begin{aligned} \mathbb{E} \Big[\max_a\epsilon_a\Big] &= \int_{-1}^1 x \dfrac{\mathbf {d}}{\mathbf{d}x} P(\max_{a} \epsilon_a \le x) \mathbf{d}x\\ &= \Big[ \Big(\dfrac{x+1}{2}\Big)^m \dfrac{mx - 1}{m+1} \Big]\bigg|_{-1}^1\\ &= \dfrac{m-1}{m+1} \end{aligned} E[amaxϵa]=∫−11xdxdP(amaxϵa≤x)dx=[(2x+1)mm+1mx−1]−11=m+1m−1
虽然这一分析简化了实际环境,但它仍然正确刻画了QQQ值过高估计的一些性质,比如QQQ值的过高估计随动作空间大小mmm的增加而增加,换言之,在动作选择数更多的环境中,QQQ值的过高估计会更严重。
8.8 参考文献
[1] HASSELT V H, GUEZ A, SILVER D. Deep reinforcement learning with double q-learning [C]// Proceedings of the AAAI conference on artificial intelligence. 2016, 30(1).
[2] WANG Z, SCHAUL T, HESSEL M, et al. Dueling network architectures for deep reinforcement learning [C]// International conference on machine learning, PMLR, 2016: 1995-2003.
[3] HESSEL M, MODAYIL J, HASSELT V H, et al. Rainbow: Combining improvements in deep reinforcement learning [C]// Thirty-second AAAI conference on artificial intelligence, 2018.
9 策略梯度算法
9.1 简介
本书之前介绍的 Q-learning、DQN 及 DQN 改进算法都是基于价值(value-based)的方法,其中 Q-learning 是处理有限状态的算法,而 DQN 可以用来解决连续状态的问题。在强化学习中,除了基于值函数的方法,还有一支非常经典的方法,那就是基于策略(policy-based)的方法。对比两者,基于值函数的方法主要是学习值函数,然后根据值函数导出一个策略,学习过程中并不存在一个显式的策略;而基于策略的方法则是直接显式地学习一个目标策略。策略梯度是基于策略的方法的基础,本章从策略梯度算法说起。
9.2 策略梯度
基于策略的方法首先需要将策略参数化。假设目标策略πθ\pi_\thetaπθ是一个随机性策略,并且处处可微,其中θ\thetaθ是对应的参数。我们可以用一个线性模型或者神经网络模型来为这样一个策略函数建模,输入某个状态,然后输出一个动作的概率分布。我们的目标是要寻找一个最优策略并最大化这个策略在环境中的期望回报。我们将策略学习的目标函数定义为
J(θ)=Es0[Vπθ(s0)]J(\theta) = \mathbb{E}_{s_0}\Big[{V^{\pi_\theta}(s_0)}\Big] J(θ)=Es0[Vπθ(s0)]
其中,s0s_0s0表示初始状态。现在有了目标函数J(θ)J(\theta)J(θ),我们将目标函数对策略θ\thetaθ求导,得到导数后,就可以用梯度上升方法来最大化这个目标函数,从而得到最优策略。
我第 3 章讲解过策略π\piπ下的状态访问分布,在此用νπ\nu^{\pi}νπ表示。然后我们对目标函数J(θ)J(\theta)J(θ)求梯度,可以得到如下式子,更详细的推导过程将在 9.6 节给出。
∇θJ(θ)∝∑s∈Sνπθ(s)∑a∈AQπθ(s,a)∇θπθ(a∣s)=∑s∈Sνπθ(s)∑a∈AQπθ(s,a)πθ(a∣s)⋅∇θπθ(a∣s)πθ(a∣s)=∑s∈Sνπθ(s)(∑a∈Aπθ(a∣s)Qπθ(s,a)⋅∇θπθ(a∣s)πθ(a∣s))=∑s∈Sνπθ(s)(∑a∈Aπθ(a∣s)Qπθ(s,a)⋅∇θlogπθ(a∣s))=Eπθ[Qπθ(s,a)∇θlogπθ(a∣s)]\begin{aligned} \nabla_\theta J(\theta) &\propto \sum_{s\in\mathcal{S}} \nu^{\pi_{\theta}}(s) \sum_{a\in\mathcal{A}}Q^{\pi_{\theta}}(s,a)\nabla_{\theta}\pi_{\theta}(a|s) \\ &= \sum_{s\in\mathcal{S}} \nu^{\pi_{\theta}}(s) \sum_{a\in\mathcal{A}}Q^{\pi_{\theta}}(s,a) \pi_{\theta}(a|s) \cdot \dfrac{\nabla_{\theta}\pi_{\theta}(a|s)}{\pi_{\theta}(a|s)} \\ &= \sum_{s\in\mathcal{S}} \nu^{\pi_{\theta}}(s) \Big( \sum_{a\in\mathcal{A}} \pi_{\theta}(a|s) Q^{\pi_{\theta}}(s,a) \cdot \dfrac{\nabla_{\theta}\pi_{\theta}(a|s)}{\pi_{\theta}(a|s)} \Big) \\ &= \sum_{s\in\mathcal{S}} \nu^{\pi_{\theta}}(s) \Big( \sum_{a\in\mathcal{A}} \pi_{\theta}(a|s) Q^{\pi_{\theta}}(s,a) \cdot \nabla_{\theta}\log \pi_{\theta}(a|s) \Big) \\ &= \mathbb{E}_{\pi_{\theta}} \Big[Q^{\pi_{\theta}}(s,a) \nabla_{\theta}\log \pi_{\theta}(a|s)\Big] \\ \end{aligned} ∇θJ(θ)∝s∈S∑νπθ(s)a∈A∑Qπθ(s,a)∇θπθ(a∣s)=s∈S∑νπθ(s)a∈A∑Qπθ(s,a)πθ(a∣s)⋅πθ(a∣s)∇θπθ(a∣s)=s∈S∑νπθ(s)(a∈A∑πθ(a∣s)Qπθ(s,a)⋅πθ(a∣s)∇θπθ(a∣s))=s∈S∑νπθ(s)(a∈A∑πθ(a∣s)Qπθ(s,a)⋅∇θlogπθ(a∣s))=Eπθ[Qπθ(s,a)∇θlogπθ(a∣s)]
这个梯度可以用来更新策略。需要注意的是,因为上式中期望E\mathbb{E}E的下标是πθ\pi_\thetaπθ,所以策略梯度算法为在线策略(on-policy)算法,即必须使用当前策略πθ\pi_\thetaπθ采样得到的数据来计算梯度。直观理解一下策略梯度这个公式,可以发现在每一个状态下,梯度的修改是让策略更多地去采样到带来较高QQQ值的动作,更少地去采样到带来较低QQQ值的动作,如图 9-1 所示。
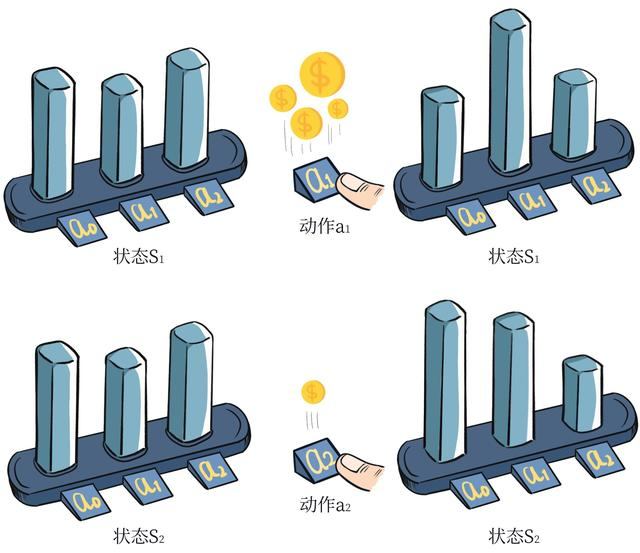
图9-1 策略梯度示意图
在计算策略梯度的公式中,我们需要用到Qπθ(s,a)Q^{\pi_{\theta}}(s,a)Qπθ(s,a),可以用多种方式对它进行估计。接下来要介绍的 REINFORCE 算法便是采用了蒙特卡洛方法来估计Qπθ(s,a)Q^{\pi_{\theta}}(s,a)Qπθ(s,a),对于一个有限步数的环境来说,REINFORCE 算法中的策略梯度为:
∇θJ(θ)=Eπθ[∑t=0T(∑t′=tTγt′−trt′)∇θlogπθ(at∣st)]\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta} \bigg[ \sum_{t=0}^T \Big( \sum_{t'=t}^T \gamma^{t'-t}r_{t'} \Big) \nabla_{\theta} \log \pi_{\theta}(a_t|s_t) \bigg] ∇θJ(θ)=Eπθ[t=0∑T(t′=t∑Tγt′−trt′)∇θlogπθ(at∣st)]
其中,TTT是和环境交互的最大步数。例如,在车杆环境中,T=200T=200T=200。
9.3 REINFORCE
REINFORCE 算法的具体算法流程如下:
- 初始化策略参数θ\thetaθ
- for 序列e=1→Ee=1\rightarrow Ee=1→E do :
- 用当前策略πθ\pi_\thetaπθ采样轨迹{s1,a1,r1,s2,a2,r2,⋯ ,sT,aT,rT}\{s_1,a_1,r_1,s_2,a_2,r_2,\cdots,s_T,a_T,r_T\}{s1,a1,r1,s2,a2,r2,⋯,sT,aT,rT}
- 计算当前轨迹每个时刻ttt往后的回报∑t′=tTγt′−trt′\displaystyle\sum_{t'=t}^T \gamma^{t'-t}r_{t'}t′=t∑Tγt′−trt′,记为ψt\psi_tψt
- 对θ\thetaθ进行更新,θ←θ+α∑t′=tTψtlogπθ(at∣st)\displaystyle\theta \leftarrow \theta + \alpha \sum_{t'=t}^{T}\psi_t\log\pi_\theta(a_t|s_t)θ←θ+αt′=t∑Tψtlogπθ(at∣st)
- end for
这便是 REINFORCE 算法的全部流程了。接下来让我们来用代码来实现它,看看效果如何吧!
9.4 REINFORCE 代码实践
我们在车杆环境中进行 REINFORCE 算法的实验。
import gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
import rl_utils
首先定义策略网络PolicyNet,其输入是某个状态,输出则是该状态下的动作概率分布,这里采用在离散动作空间上的softmax()函数来实现一个可学习的多项分布(multinomial distribution)。
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
再定义我们的 REINFORCE 算法。在函数take_action()函数中,我们通过动作概率分布对离散的动作进行采样。在更新过程中,我们按照算法将损失函数写为策略回报的负数,即−∑tψt∇θlogπθ(at∣st)\displaystyle-\sum\limits_t\psi_t\nabla_\theta \log\pi_\theta(a_t|s_t)−t∑ψt∇θlogπθ(at∣st),对求导后就可以通过梯度下降来更新策略。
class REINFORCE:
def __init__(
self,
state_dim,
hidden_dim,
action_dim,
learning_rate,
gamma,
device
):
self.policy_net = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.optimizer = torch.optim.Adam(self.policy_net.parameters(), lr=learning_rate) # 使用Adam优化器
self.gamma = gamma # 折扣因子
self.device = device
def take_action(self, state): # 根据动作概率分布随机采样
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.policy_net(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self, transition_dict):
reward_list = transition_dict['rewards']
state_list = transition_dict['states']
action_list = transition_dict['actions']
G = 0
self.optimizer.zero_grad()
for i in reversed(range(len(reward_list))): # 从最后一步算起
reward = reward_list[i]
state = torch.tensor([state_list[i]], dtype=torch.float).to(self.device)
action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
log_prob = torch.log(self.policy_net(state).gather(1, action))
G = self.gamma * G + reward
loss = -log_prob * G # 每一步的损失函数
loss.backward() # 反向传播计算梯度
self.optimizer.step() # 梯度下降
定义好策略,我们就可以开始实验了,看看 REINFORCE 算法在车杆环境上表现如何吧!
learning_rate = 1e-3
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = "CartPole-v0"
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = REINFORCE(
state_dim,
hidden_dim,
action_dim,
learning_rate,
gamma,
device
)
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
transition_dict = {
'states': [],
'actions': [],
'next_states': [],
'rewards': [],
'dones': []
}
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done, _ = env.step(action)
transition_dict['states'].append(state)
transition_dict['actions'].append(action)
transition_dict['next_states'].append(next_state)
transition_dict['rewards'].append(reward)
transition_dict['dones'].append(done)
state = next_state
episode_return += reward
return_list.append(episode_return)
agent.update(transition_dict)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
Iteration 0: 100%|██████████████████████████████████████| 100/100 [00:02<00:00, 47.36it/s, episode=100, return=55.500]
Iteration 1: 100%|██████████████████████████████████████| 100/100 [00:04<00:00, 21.26it/s, episode=200, return=75.300]
Iteration 2: 100%|██████████████████████████████████████| 100/100 [00:09<00:00, 10.55it/s, episode=300, return=178.800]
Iteration 3: 100%|██████████████████████████████████████| 100/100 [00:11<00:00, 8.74it/s, episode=400, return=164.600]
Iteration 4: 100%|██████████████████████████████████████| 100/100 [00:11<00:00, 8.74it/s, episode=500, return=156.500]
Iteration 5: 100%|██████████████████████████████████████| 100/100 [00:11<00:00, 8.54it/s, episode=600, return=187.400]
Iteration 6: 100%|██████████████████████████████████████| 100/100 [00:11<00:00, 8.52it/s, episode=700, return=194.500]
Iteration 7: 100%|██████████████████████████████████████| 100/100 [00:13<00:00, 7.57it/s, episode=800, return=200.000]
Iteration 8: 100%|██████████████████████████████████████| 100/100 [00:12<00:00, 7.84it/s, episode=900, return=200.000]
Iteration 9: 100%|██████████████████████████████████████| 100/100 [00:12<00:00, 7.89it/s, episode=1000, return=186.100]
在 CartPole-v0 环境中,满分就是 200 分,我们发现 REINFORCE 算法效果很好,可以达到 200 分。接下来我们绘制训练过程中每一条轨迹的回报变化图。由于回报抖动比较大,往往会进行平滑处理。
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.show()

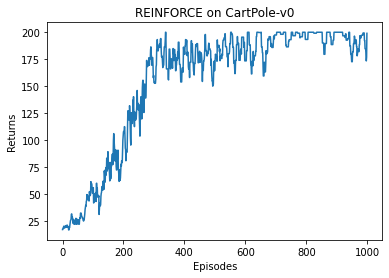
可以看到,随着收集到的轨迹越来越多,REINFORCE 算法有效地学习到了最优策略。不过,相比于前面的 DQN 算法,REINFORCE 算法使用了更多的序列,这是因为 REINFORCE 算法是一个在线策略算法,之前收集到的轨迹数据不会被再次利用。此外,REINFORCE 算法的性能也有一定程度的波动,这主要是因为每条采样轨迹的回报值波动比较大,这也是 REINFORCE 算法主要的不足。
9.5 小结
REINFORCE 算法是策略梯度乃至强化学习的典型代表,智能体根据当前策略直接和环境交互,通过采样得到的轨迹数据直接计算出策略参数的梯度,进而更新当前策略,使其向最大化策略期望回报的目标靠近。这种学习方式是典型的从交互中学习,并且其优化的目标(即策略期望回报)正是最终所使用策略的性能,这比基于价值的强化学习算法的优化目标(一般是时序差分误差的最小化)要更加直接。 REINFORCE 算法理论上是能保证局部最优的,它实际上是借助蒙特卡洛方法采样轨迹来估计动作价值,这种做法的一大优点是可以得到无偏的梯度。但是,正是因为使用了蒙特卡洛方法,REINFORCE 算法的梯度估计的方差很大,可能会造成一定程度上的不稳定,这也是第 10 章将介绍的 Actor-Critic 算法要解决的问题。
9.6 扩展阅读:策略梯度证明
策略梯度定理是强化学习中的重要理论。本节我们来证明
∇θJ(θ)∝∑s∈Sνπθ(s)∑a∈AQπθ(s,a)∇θπθ(a∣s)\nabla_\theta J(\theta) \propto \sum_{s\in\mathcal{S}} \nu^{\pi_\theta}(s) \sum_{a\in\mathcal{A}} Q^{\pi_\theta}(s,a)\nabla_\theta \pi_\theta(a|s) ∇θJ(θ)∝s∈S∑νπθ(s)a∈A∑Qπθ(s,a)∇θπθ(a∣s)
先从状态价值函数的推导开始:
∇θVπθ(s)=∇θ(∑a∈Aπθ(a∣s)Qπθ(s,a))=∑a∈A(Qπθ(s,a)∇θπθ(a∣s)+πθ(a∣s)∇θQπθ(s,a))=∑a∈A(Qπθ(s,a)∇θπθ(a∣s))+∑a∈A(πθ(a∣s)∇θQπθ(s,a))=∑a∈A(Qπθ(s,a)∇θπθ(a∣s))+∑a∈Aπθ(a∣s)∇θ(∑s′,rp(s′,r∣s,a)(r+γVπθ(s′)))=∑a∈A(Qπθ(s,a)∇θπθ(a∣s))+∑a∈Aπθ(a∣s)(∑s′,rp(s′,r∣s,a)∇θ(r+γVπθ(s′)))=∑a∈A(Qπθ(s,a)∇θπθ(a∣s))+∑a∈Aπθ(a∣s)(∑s′,rp(s′,r∣s,a)∇θ(γVπθ(s′)))=∑a∈A(Qπθ(s,a)∇θπθ(a∣s))+γ∑a∈Aπθ(a∣s)(∑s′p(s′∣s,a)∇θVπθ(s′))\begin{aligned} \nabla_\theta V^{\pi_\theta}(s) &= \nabla_\theta \Big( \sum_{a\in\mathcal{A}}\pi_\theta (a|s) Q^{\pi_\theta}(s,a) \Big)\\ &= \sum_{a\in\mathcal{A}} \Big( Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s) + \pi_\theta (a|s) \nabla_\theta Q^{\pi_\theta}(s,a) \Big)\\ &= \sum_{a\in\mathcal{A}} \Big( Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s) \Big) + \sum_{a\in\mathcal{A}} \Big( \pi_\theta (a|s) \nabla_\theta Q^{\pi_\theta}(s,a)\Big) \\ &= \sum_{a\in\mathcal{A}} \Big( Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s) \Big) + \sum_{a\in\mathcal{A}} \pi_\theta (a|s) \nabla_\theta \bigg( \sum_{s',r} p(s',r|s,a)\Big(r+\gamma V^{\pi_\theta}(s')\Big) \bigg) \\ &= \sum_{a\in\mathcal{A}} \Big( Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s) \Big) + \sum_{a\in\mathcal{A}} \pi_\theta (a|s) \bigg( \sum_{s',r} p(s',r|s,a) \nabla_\theta \Big(r+\gamma V^{\pi_\theta}(s')\Big) \bigg) \\ &= \sum_{a\in\mathcal{A}} \Big( Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s) \Big) + \sum_{a\in\mathcal{A}} \pi_\theta (a|s) \bigg( \sum_{s',r} p(s',r|s,a) \nabla_\theta \Big(\gamma V^{\pi_\theta}(s')\Big) \bigg) \\ &= \sum_{a\in\mathcal{A}} \Big( Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s) \Big) + \gamma \sum_{a\in\mathcal{A}} \pi_\theta (a|s) \Big( \sum_{s'} p(s'|s,a) \nabla_\theta V^{\pi_\theta}(s') \Big) \end{aligned} ∇θVπθ(s)=∇θ(a∈A∑πθ(a∣s)Qπθ(s,a))=a∈A∑(Qπθ(s,a)∇θπθ(a∣s)+πθ(a∣s)∇θQπθ(s,a))=a∈A∑(Qπθ(s,a)∇θπθ(a∣s))+a∈A∑(πθ(a∣s)∇θQπθ(s,a))=a∈A∑(Qπθ(s,a)∇θπθ(a∣s))+a∈A∑πθ(a∣s)∇θ(s′,r∑p(s′,r∣s,a)(r+γVπθ(s′)))=a∈A∑(Qπθ(s,a)∇θπθ(a∣s))+a∈A∑πθ(a∣s)(s′,r∑p(s′,r∣s,a)∇θ(r+γVπθ(s′)))=a∈A∑(Qπθ(s,a)∇θπθ(a∣s))+a∈A∑πθ(a∣s)(s′,r∑p(s′,r∣s,a)∇θ(γVπθ(s′)))=a∈A∑(Qπθ(s,a)∇θπθ(a∣s))+γa∈A∑πθ(a∣s)(s′∑p(s′∣s,a)∇θVπθ(s′))
为了简化表示,我们让ϕ(s)=∑a∈AQπθ(s,a)∇θπθ(a∣s)\displaystyle \phi(s) = \sum\limits_{a\in\mathcal{A}}Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s)ϕ(s)=a∈A∑Qπθ(s,a)∇θπθ(a∣s), 定义dπθ(s→x,k)d^{\pi_\theta}(s\rightarrow x,k)dπθ(s→x,k)为策略π\piπ从状态sss出发kkk步后到达状态xxx的概率。我们继续推导:
∇θVπθ(s)=ϕ(s)+γ∑a∈Aπθ(a∣s)(∑s′p(s′∣s,a)∇θVπθ(s′))=ϕ(s)+γ∑a∈A∑s′πθ(a∣s)p(s′∣s,a)∇θVπθ(s′)=ϕ(s)+γ∑s′dπθ(s→s′,1)∇θVπθ(s′)(利用该递推式)=ϕ(s)+γ∑s′dπθ(s→s′,1)[ϕ(s′)+γ∑s′′dπθ(s′→s′′,1)∇θVπθ(s′′)]=ϕ(s)+γ∑s′dπθ(s→s′,1)ϕ(s′)+γ2∑s′′dπθ(s→s′′,2)∇θVπθ(s′′)=ϕ(s)+γ∑s′dπθ(s→s′,1)ϕ(s′)+γ2∑s′′dπθ(s→s′′,2)ϕ(s′′)+γ3∑s′′′dπθ(s→s′′′,3)∇θVπθ(s′′′)=⋯=∑s∈S∑k=0∞γkdπθ(s0→s,k)ϕ(x)\begin{aligned} \nabla_\theta V^{\pi_\theta}(s) &= \phi(s) + \gamma \sum_{a\in\mathcal{A}} \pi_\theta (a|s) \Big( \sum_{s'} p(s'|s,a) \nabla_\theta V^{\pi_\theta}(s') \Big)\\ &= \phi(s) + \gamma \sum_{a\in\mathcal{A}} \sum_{s'} \pi_\theta (a|s) p(s'|s,a) \nabla_\theta V^{\pi_\theta}(s')\\ &= \phi(s) + \gamma \sum_{s'} d^{\pi_\theta}(s\rightarrow s',1) \nabla_\theta V^{\pi_\theta}(s') \quad (\text{利用该递推式})\\ &= \phi(s) + \gamma \sum_{s'} d^{\pi_\theta}(s\rightarrow s',1) \Big[ \phi(s') + \gamma \sum_{s''} d^{\pi_\theta}(s'\rightarrow s'',1) \nabla_\theta V^{\pi_\theta}(s'') \Big]\\ &= \phi(s) + \gamma \sum_{s'} d^{\pi_\theta}(s\rightarrow s',1) \phi(s') + \gamma^2 \sum_{s''} d^{\pi_\theta}(s\rightarrow s'',2) \nabla_\theta V^{\pi_\theta}(s'')\\ &= \phi(s) + \gamma \sum_{s'} d^{\pi_\theta}(s\rightarrow s',1) \phi(s') + \gamma^2 \sum_{s''} d^{\pi_\theta}(s\rightarrow s'',2) \phi(s'') + \gamma^3 \sum_{s'''} d^{\pi_\theta}(s\rightarrow s''',3) \nabla_\theta V^{\pi_\theta}(s''')\\ &= \cdots\\ &= \sum_{s\in\mathcal{S}}\sum_{k=0}^\infin \gamma^kd^{\pi_\theta}(s_0\rightarrow s,k)\phi(x) \end{aligned} ∇θVπθ(s)=ϕ(s)+γa∈A∑πθ(a∣s)(s′∑p(s′∣s,a)∇θVπθ(s′))=ϕ(s)+γa∈A∑s′∑πθ(a∣s)p(s′∣s,a)∇θVπθ(s′)=ϕ(s)+γs′∑dπθ(s→s′,1)∇θVπθ(s′)(利用该递推式)=ϕ(s)+γs′∑dπθ(s→s′,1)[ϕ(s′)+γs′′∑dπθ(s′→s′′,1)∇θVπθ(s′′)]=ϕ(s)+γs′∑dπθ(s→s′,1)ϕ(s′)+γ2s′′∑dπθ(s→s′′,2)∇θVπθ(s′′)=ϕ(s)+γs′∑dπθ(s→s′,1)ϕ(s′)+γ2s′′∑dπθ(s→s′′,2)ϕ(s′′)+γ3s′′′∑dπθ(s→s′′′,3)∇θVπθ(s′′′)=⋯=s∈S∑k=0∑∞γkdπθ(s0→s,k)ϕ(x)
定义η(s)=Es0[∑k=0∞γkdπθ(s0→s,k)]\displaystyle \eta(s) = \mathbb{E}_{s_0}\Big[\sum_{k=0}^\infin \gamma^kd^{\pi_\theta}(s_0\rightarrow s,k)\Big]η(s)=Es0[k=0∑∞γkdπθ(s0→s,k)]。至此,回到目标函数:
∇θJ(θ)=∇θEs0[Vπθ(s0)]=∑s∈SEs0[∑k=0∞γkdπθ(s0→s,k)]ϕ(x)=∑s∈Sη(s)ϕ(x)=∑s∈Sη(s)⋅1⋅ϕ(x)=∑s∈Sη(s)⋅(∑s∈Sη(s)∑s∈Sη(s))⋅ϕ(x)∝(∑s∈Sη(s)∑s∈Sη(s))⋅ϕ(x)=(∑s∈Sη(s)∑s∈Sη(s))⋅(∑a∈AQπθ(s,a)∇θπθ(a∣s))=∑s∈Sνπθ(s)∑a∈AQπθ(s,a)∇θπθ(a∣s)\begin{aligned} \nabla_\theta J(\theta) &= \nabla_\theta \mathbb{E}_{s_0} \Big[ V^{\pi_\theta}(s_0) \Big] \\ &= \sum_{s\in\mathcal{S}} \mathbb{E}_{s_0} \bigg[\sum_{k=0}^\infin \gamma^kd^{\pi_\theta}(s_0\rightarrow s,k)\bigg]\phi(x) \\ &= \sum_{s\in\mathcal{S}} \eta(s)\phi(x) \\ &= \sum_{s\in\mathcal{S}} \eta(s) \cdot 1 \cdot \phi(x) \\ &= \sum_{s\in\mathcal{S}} \eta(s) \cdot \bigg(\sum_{s\in\mathcal{S}} \dfrac{\eta(s)}{\displaystyle \sum_{s\in\mathcal{S}} \eta(s)}\bigg) \cdot \phi(x) \\ &\propto \bigg(\sum_{s\in\mathcal{S}} \dfrac{\eta(s)}{\displaystyle \sum_{s\in\mathcal{S}} \eta(s)}\bigg) \cdot \phi(x) \\ &= \bigg(\sum_{s\in\mathcal{S}} \dfrac{\eta(s)}{\displaystyle \sum_{s\in\mathcal{S}} \eta(s)} \bigg) \cdot \bigg( \sum\limits_{a\in\mathcal{A}}Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s)\bigg) \\ &= \sum_{s\in\mathcal{S}} \nu^{\pi_\theta}(s) \sum\limits_{a\in\mathcal{A}}Q^{\pi_\theta}(s,a) \nabla_\theta\pi_\theta (a|s) \\ \end{aligned} ∇θJ(θ)=∇θEs0[Vπθ(s0)]=s∈S∑Es0[k=0∑∞γkdπθ(s0→s,k)]ϕ(x)=s∈S∑η(s)ϕ(x)=s∈S∑η(s)⋅1⋅ϕ(x)=s∈S∑η(s)⋅(s∈S∑s∈S∑η(s)η(s))⋅ϕ(x)∝(s∈S∑s∈S∑η(s)η(s))⋅ϕ(x)=(s∈S∑s∈S∑η(s)η(s))⋅(a∈A∑Qπθ(s,a)∇θπθ(a∣s))=s∈S∑νπθ(s)a∈A∑Qπθ(s,a)∇θπθ(a∣s)
证明完毕!
9.7 参考文献
[1] SUTTON R S, MCALLESTER D A, SINGH S P, et al. Policy gradient methods for reinforcement learning with function approximation [C] // Advances in neural information processing systems, 2000: 1057-1063.
10 Actor-Critic 算法
10.1 简介
本书之前的章节讲解了基于值函数的方法(DQN)和基于策略的方法(REINFORCE),其中基于值函数的方法只学习一个价值函数,而基于策略的方法只学习一个策略函数。那么,一个很自然的问题是,有没有什么方法既学习价值函数,又学习策略函数呢?答案就是 Actor-Critic。Actor-Critic 是囊括一系列算法的整体架构,目前很多高效的前沿算法都属于 Actor-Critic 算法,本章接下来将会介绍一种最简单的 Actor-Critic 算法。需要明确的是,Actor-Critic 算法本质上是基于策略的算法,因为这一系列算法的目标都是优化一个带参数的策略,只是会额外学习价值函数,从而帮助策略函数更好地学习。
10.2 Actor-Critic
回顾一下,在 REINFORCE 算法中,目标函数的梯度中有一项轨迹回报,用于指导策略的更新。REINFOCE 算法用蒙特卡洛方法来估计Q(s,a)Q(s,a)Q(s,a),能不能考虑拟合一个值函数来指导策略进行学习呢?这正是 Actor-Critic 算法所做的。在策略梯度中,可以把梯度写成下面这个更加一般的形式:
g=E[∑t=0Tψt∇θlogπθ(at∣st)]g = \mathbb{E} \Big[ \sum_{t=0}^T \psi_t \nabla_\theta \log \pi_\theta (a_t|s_t) \Big] g=E[t=0∑Tψt∇θlogπθ(at∣st)]
其中,ψt\psi_tψt可以有很多种形式:
(1) ∑t′=0Tγt′rt′\displaystyle \sum_{t'=0}^T \gamma^{t'}r_{t'}t′=0∑Tγt′rt′:轨迹的总回报;
(2) ∑t′=tTγt′−trt′\displaystyle \sum_{t'=t}^T \gamma^{t' - t}r_{t'}t′=t∑Tγt′−trt′:动作ata_tat之后的回报;
(3) ∑t′=tTγt′−trt′−b(st)\displaystyle \sum_{t'=t}^T \gamma^{t'-t}r_{t'} - b(s_t)t′=t∑Tγt′−trt′−b(st):基准线版本的改进;
(4) Qπθ(st,at)Q^{\pi_\theta}(s_t,a_t)Qπθ(st,at):动作价值函数
(5) Aπθ(st,at)A^{\pi_\theta}(s_t,a_t)Aπθ(st,at):优势函数
(6) rt+γVπθ(st+1)−Vπθ(st)r_t + \gamma V^{\pi_{\theta}}(s_{t+1}) - V^{\pi_{\theta}}(s_t)rt+γVπθ(st+1)−Vπθ(st):时序差分残差
9.5 节提到 REINFORCE 通过蒙特卡洛采样的方法对策略梯度的估计是无偏的,但是方差非常大。我们可以用形式(3)引入基线函数(baseline function)b(st)b(s_t)b(st)来减小方差。此外,我们也可以采用 Actor-Critic 算法估计一个动作价值函数QQQ,代替蒙特卡洛采样得到的回报,这便是形式(4)。这个时候,我们可以把状态价值函数VVV作为基线,从QQQ函数减去这个VVV函数则得到了AAA函数,我们称之为优势函数(advantage function),这便是形式(5)。更进一步,我们可以利用Q=r+γVQ=r+\gamma VQ=r+γV等式得到形式(6)。
本章将着重介绍形式(6),即通过时序差分残差ψt=rt+γVπ(st+1)−Vπ(st)\psi_t = r_t + \gamma V^{\pi}(s_{t+1}) - V^{\pi}(s_t)ψt=rt+γVπ(st+1)−Vπ(st)来指导策略梯度进行学习。事实上,用QQQ值或者VVV值本质上也是用奖励来进行指导,但是用神经网络进行估计的方法可以减小方差、提高鲁棒性。除此之外,REINFORCE 算法基于蒙特卡洛采样,只能在序列结束后进行更新,这同时也要求任务具有有限的步数,而 Actor-Critic 算法则可以在每一步之后都进行更新,并且不对任务的步数做限制。
我们将 Actor-Critic 分为两个部分:Actor(策略网络)和 Critic(价值网络),如图 10-1 所示。
- Actor 要做的是与环境交互,并在 Critic 价值函数的指导下用策略梯度学习一个更好的策略。
- Critic 要做的是通过 Actor 与环境交互收集的数据学习一个价值函数,这个价值函数会用于判断在当前状态什么动作是好的,什么动作不是好的,进而帮助 Actor 进行策略更新。

图10-1 Actor 和 Critic 的关系
Actor 的更新采用策略梯度的原则,那 Critic 如何更新呢?我们将 Critic 价值网络表示为VωV_\omegaVω,参数为ω\omegaω。于是,我们可以采取时序差分残差的学习方式,对于单个数据定义如下价值函数的损失函数:
L(ω)=12(r+γVω(st+1)−Vω(st))2\mathcal{L}(\omega) = \dfrac{1}{2} \Big(r + \gamma V_{\omega}(s_{t+1}) - V_{\omega}(s_t)\Big)^2 L(ω)=21(r+γVω(st+1)−Vω(st))2
与 DQN 中一样,我们采取类似于目标网络的方法,将上式中r+γVω(st+1)r + \gamma V_{\omega}(s_{t+1})r+γVω(st+1)作为时序差分目标,不会产生梯度来更新价值函数。因此,价值函数的梯度为:
∇ωL(ω)=−(r+γVω(st+1)−Vω(st))∇ωVω(st)\nabla_{\omega}\mathcal{L}(\omega) = - \Big( r + \gamma V_{\omega}(s_{t+1}) - V_{\omega}(s_t) \Big) \nabla_{\omega} V_{\omega}(s_t) ∇ωL(ω)=−(r+γVω(st+1)−Vω(st))∇ωVω(st)
然后使用梯度下降方法来更新 Critic 价值网络参数即可。
Actor-Critic 算法的具体流程如下:
- 初始化策略网络参数θ\thetaθ,价值网络参数ω\omegaω
- for 序列 e=1→Ee=1\rightarrow Ee=1→E do :
- 用当前策略πθ\pi_\thetaπθ采样轨迹{s1,a1,r1,s2,a2,r2,⋯}\Big\{ s_1,a_1,r_1,s_2,a_2,r_2,\cdots \Big\}{s1,a1,r1,s2,a2,r2,⋯}
- 为每一步数据计算: δt=rt+γVω(st+1)−Vω(st)\delta_t = r_t + \gamma V_{\omega}(s_{t+1}) - V_{\omega}(s_t)δt=rt+γVω(st+1)−Vω(st)
- 更新价值参数 ω=ω+αω∑tδt∇ωVω(st)\displaystyle \omega = \omega + \alpha_\omega \sum_t \delta_t \nabla_\omega V_\omega (s_t)ω=ω+αωt∑δt∇ωVω(st)
- 更新策略参数 θ=θ+αθ∑tδt∇θlogπθ(at∣st)\displaystyle \theta = \theta + \alpha_\theta \sum_t \delta_t \nabla_\theta \log \pi_\theta(a_t|s_t)θ=θ+αθt∑δt∇θlogπθ(at∣st)
- end for
以上就是 Actor-Critic 算法的流程,接下来让我们来用代码实现它,看看效果如何吧!
10.3 Actor-Critic 代码实践
我们仍然在车杆环境上进行 Actor-Critic 算法的实验。
import gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
import rl_utils
首先定义策略网络PolicyNet(与 REINFORCE 算法一样)。
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
Actor-Critic 算法中额外引入一个价值网络,接下来的代码定义价值网络ValueNet,其输入是某个状态,输出则是状态的价值。
class ValueNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim):
super(ValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
现在定义ActorCritic算法,主要包含采取动作(take_action())和更新网络参数(update())两个函数。
class ActorCritic:
def __init__(
self,
state_dim,
hidden_dim,
action_dim,
actor_lr,
critic_lr,
gamma,
device
):
# 策略网络
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device) # 价值网络
# 策略网络优化器
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr) # 价值网络优化器
self.gamma = gamma
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
# 时序差分目标
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones)
td_delta = td_target - self.critic(states) # 时序差分误差
log_probs = torch.log(self.actor(states).gather(1, actions))
actor_loss = torch.mean(-log_probs * td_delta.detach())
# 均方误差损失函数
critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward() # 计算策略网络的梯度
critic_loss.backward() # 计算价值网络的梯度
self.actor_optimizer.step() # 更新策略网络的参数
self.critic_optimizer.step() # 更新价值网络的参数
定义好 Actor 和 Critic,我们就可以开始实验了,看看 Actor-Critic 在车杆环境上表现如何吧!
actor_lr = 1e-3
critic_lr = 1e-2
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = ActorCritic(
state_dim,
hidden_dim,
action_dim,
actor_lr,
critic_lr,
gamma,
device
)
return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
Iteration 0: 100%|██████████| 100/100 [00:00<00:00, 101.75it/s, episode=100, return=21.100]
Iteration 1: 100%|██████████| 100/100 [00:01<00:00, 58.71it/s, episode=200, return=72.800]
Iteration 2: 100%|██████████| 100/100 [00:05<00:00, 19.73it/s, episode=300, return=109.300]
Iteration 3: 100%|██████████| 100/100 [00:05<00:00, 17.30it/s, episode=400, return=163.000]
Iteration 4: 100%|██████████| 100/100 [00:06<00:00, 16.27it/s, episode=500, return=193.600]
Iteration 5: 100%|██████████| 100/100 [00:06<00:00, 15.90it/s, episode=600, return=195.900]
Iteration 6: 100%|██████████| 100/100 [00:06<00:00, 15.80it/s, episode=700, return=199.100]
Iteration 7: 100%|██████████| 100/100 [00:06<00:00, 15.72it/s, episode=800, return=186.900]
Iteration 8: 100%|██████████| 100/100 [00:06<00:00, 15.94it/s, episode=900, return=200.000]
Iteration 9: 100%|██████████| 100/100 [00:06<00:00, 15.45it/s, episode=1000, return=200.000]
在 CartPole-v0 环境中,满分就是 200 分。和 REINFORCE 相似,接下来我们绘制训练过程中每一条轨迹的回报变化图以及其经过平滑处理的版本。
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()

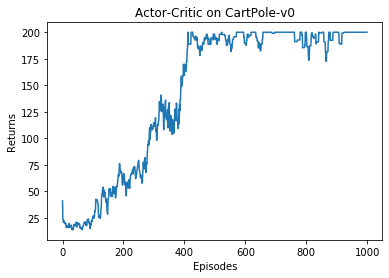
根据实验结果我们可以发现,Actor-Critic 算法很快便能收敛到最优策略,并且训练过程非常稳定,抖动情况相比 REINFORCE 算法有了明显的改进,这说明价值函数的引入减小了方差。
10.4 总结
本章讲解了 Actor-Critic 算法,它是基于值函数的方法和基于策略的方法的叠加。价值模块 Critic 在策略模块 Actor 采样的数据中学习分辨什么是好的动作,什么不是好的动作,进而指导 Actor 进行策略更新。随着 Actor 的训练的进行,其与环境交互所产生的数据分布也发生改变,这需要 Critic 尽快适应新的数据分布并给出好的判别。
Actor-Critic 算法非常实用,后续章节中的 TRPO、PPO、DDPG、SAC 等深度强化学习算法都是在 Actor-Critic 框架下进行发展的。深入了解 Actor-Critic 算法对读懂目前深度强化学习的研究热点大有裨益。
10.5 参考文献
[1] KONDA, V R, TSITSIKLIS J N. Actor-critic algorithms [C]// Advances in neural information processing systems, 2000.
11 TRPO 算法
11.1 简介
本书之前介绍的基于策略的方法包括策略梯度算法和 Actor-Critic 算法。这些方法虽然简单、直观,但在实际应用过程中会遇到训练不稳定的情况。回顾一下基于策略的方法:参数化智能体的策略,并设计衡量策略好坏的目标函数,通过梯度上升的方法来最大化这个目标函数,使得策略最优。具体来说,假设 θ\thetaθ 表示策略 πθ\pi_\thetaπθ 的参数,定义J(θ)=Eπθ[Vπθ(s0)]=Eπθ[∑t=0∞γtr(st,at)]\displaystyle J(\theta)=\mathbb{E}_{\pi_{\theta}}[V^{\pi_\theta}(s_0)]=\mathbb{E}_{\pi_{\theta}}[\sum_{t=0}^\infin \gamma^t r(s_t,a_t)]J(θ)=Eπθ[Vπθ(s0)]=Eπθ[t=0∑∞γtr(st,at)],基于策略的方法的目标是找到θ∗=arg maxθJ(θ)\theta^*=\underset{\theta}{\argmax}J(\theta)θ∗=θargmaxJ(θ),策略梯度算法主要沿着 ∇θJ(θ)\nabla_\theta J(\theta)∇θJ(θ) 方向迭代更新策略参数θ\thetaθ。但是这种算法有一个明显的缺点:当策略网络是深度模型时,沿着策略梯度更新参数,很有可能由于步长太长,策略突然显著变差,进而影响训练效果。
针对以上问题,我们考虑在更新时找到一块信任区域(trust region),在这个区域上更新策略时能够得到某种策略性能的安全性保证,这就是信任区域策略优化(trust region policy optimization,TRPO)算法的主要思想。TRPO 算法在 2015 年被提出,它在理论上能够保证策略学习的性能单调性,并在实际应用中取得了比策略梯度算法更好的效果。
11.2 策略目标
策略梯度优化目标有两种表达形式:J(θ)=Eπθ[Vπθ(s0)]J(\theta) = \mathbb{E}_{\pi_{\theta}}[V^{\pi_\theta}(s_0)]J(θ)=Eπθ[Vπθ(s0)] 第一种是根据cumulative discounted reward设计的,形式为:J(θ)=Eτ∼pθ(τ)[∑t∞γtr(st,at)]\displaystyle J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [\sum_t^{\infin} \gamma^t r(s_t, a_t)]J(θ)=Eτ∼pθ(τ)[t∑∞γtr(st,at)] 因为 Vπθ(s)=Ea∼πθ(s)[Qπθ(s,a)]=Ea∼πθ(s)[Eτ∼pθ(τ)[∑sk=s,ak=a∑t=k∞γt−kr(st,at)]]\displaystyle V^{\pi_\theta}(s) = \mathbb{E}_{a\sim \pi_\theta(s)}[Q^{\pi_\theta}(s,a)] = \mathbb{E}_{a\sim \pi_\theta(s)}\Big[\mathbb{E}_{\tau \sim p_{\theta}(\tau)} [\sum_{s_k=s, a_k=a} \sum_{t=k}^{\infin} \gamma^{t-k} r(s_t,a_t)]\Big]Vπθ(s)=Ea∼πθ(s)[Qπθ(s,a)]=Ea∼πθ(s)[Eτ∼pθ(τ)[sk=s,ak=a∑t=k∑∞γt−kr(st,at)]] 第二种是根据s0s_0s0的distribution来设计的,形式为:J(θ)=Es0∼pθ(s0)[Vπθ(s0)]J(\theta) = \mathbb{E}_{s_0 \sim p_{\theta}(s_0)}[V^{\pi_\theta}(s_0)]J(θ)=Es0∼pθ(s0)[Vπθ(s0)]
假设当前策略为πθ\pi_\thetaπθ,参数为θ\thetaθ。我们考虑如何借助当前的θ\thetaθ找到一个更优的参数θ′\theta'θ′,使得J(θ′)≥J(θ)J(\theta')\ge J(\theta)J(θ′)≥J(θ)。具体来说,由于初始状态s0s_0s0的分布和策略无关,因此上述策略πθ\pi_\thetaπθ下的优化目标J(θ)J(\theta)J(θ)可以写成在新策略πθ′\pi_{\theta'}πθ′的期望形式:
s0s_0s0只与环境有关,所以s0s_0s0的概率与根据策略πθ\pi_{\theta}πθ采样得到的轨迹τ\tauτ中的第一个状态s0s_0s0的概率是一样的。 这样就可以对期望的因子进行换元,由 s0s_0s0 变成 τ\tauτ,然后采 τ\tauτ 里的 s0s_0s0。
J(θ)=Es0∼p(s0)[Vπθ(s0)]=Eτ∼pθ′(τ)[Vπθ(s0)]=Eτ∼pθ′(τ)[Vπθ(s0)+∑t=1∞γtVπθ(st)−∑t=1∞γtVπθ(st)]=Eτ∼pθ′(τ)[∑t=0∞γtVπθ(st)−∑t=1∞γtVπθ(st)]=−Eτ∼pθ′(τ)[∑t=1∞γtVπθ(st)−∑t=0∞γtVπθ(st)]=−Eτ∼pθ′(τ)[∑t=0∞γt+1Vπθ(st+1)−∑t=0∞γtVπθ(st)]=−Eτ∼pθ′(τ)[∑t=0∞γt(γVπθ(st+1)−Vπθ(st))]\begin{aligned} J(\theta) &= \mathbb{E}_{s_0\sim p(s_0)} [V^{\pi_\theta}(s_0)]\\ &= \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} [V^{\pi_\theta}(s_0)]\\ &= \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} \bigg[V^{\pi_\theta}(s_0) + \sum_{t=1}^\infin \gamma^t V^{\pi_{\theta}}(s_t) - \sum_{t=1}^\infin \gamma^t V^{\pi_{\theta}}(s_t)\bigg]\\ &= \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} \bigg[\sum_{t=0}^\infin \gamma^tV^{\pi_\theta}(s_t) - \sum_{t=1}^\infin \gamma^t V^{\pi_{\theta}}(s_t)\bigg]\\ &= -\mathbb{E}_{\tau \sim p_{\theta'}(\tau)} \bigg[\sum_{t=1}^\infin \gamma^t V^{\pi_{\theta}}(s_t) - \sum_{t=0}^\infin \gamma^tV^{\pi_\theta}(s_t)\bigg]\\ &= -\mathbb{E}_{\tau \sim p_{\theta'}(\tau)} \bigg[\sum_{t=0}^\infin \gamma^{t+1} V^{\pi_{\theta}}(s_{t+1}) - \sum_{t=0}^\infin \gamma^tV^{\pi_\theta}(s_t)\bigg]\\ &= -\mathbb{E}_{\tau \sim p_{\theta'}(\tau)} \bigg[\sum_{t=0}^\infin \gamma^t \Big(\gamma V^{\pi_\theta}(s_{t+1}) - V^{\pi_{\theta}}(s_t)\Big)\bigg]\\ \end{aligned} J(θ)=Es0∼p(s0)[Vπθ(s0)]=Eτ∼pθ′(τ)[Vπθ(s0)]=Eτ∼pθ′(τ)[Vπθ(s0)+t=1∑∞γtVπθ(st)−t=1∑∞γtVπθ(st)]=Eτ∼pθ′(τ)[t=0∑∞γtVπθ(st)−t=1∑∞γtVπθ(st)]=−Eτ∼pθ′(τ)[t=1∑∞γtVπθ(st)−t=0∑∞γtVπθ(st)]=−Eτ∼pθ′(τ)[t=0∑∞γt+1Vπθ(st+1)−t=0∑∞γtVπθ(st)]=−Eτ∼pθ′(τ)[t=0∑∞γt(γVπθ(st+1)−Vπθ(st))]
基于以上等式,我们可以推导新旧策略的目标函数之间的差距:
前面用第一种形式(cumulative discounted reward)展开,后面一个根据上面推导的形式展开
J(θ′)−J(θ)=Es0[Vπθ′(s0)]−Es0[Vπθ(s0)]=Eτ∼pθ′(τ)[∑t=0∞γtr(st,at)]+Eτ∼pθ′(τ)[∑t=0∞γt(γVπθ(st+1)−Vπθ(st))]=Eτ∼pθ′(τ)[∑t=0∞γt(r(st,at)+γVπθ(st+1)−Vπθ(st))]\begin{aligned} J(\theta') - J(\theta) &= \mathbb{E}_{s_0}[V^{\pi_{\theta'}}(s_0)] - \mathbb{E}_{s_0}[V^{\pi_{\theta}}(s_0)] \\ &= \mathbb{E}_{\tau \sim p_{\theta'}(\tau)}\Big[ \sum_{t=0}^\infin \gamma^tr(s_t,a_t) \Big] + \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} \bigg[\sum_{t=0}^\infin \gamma^t \Big(\gamma V^{\pi_\theta}(s_{t+1}) - V^{\pi_{\theta}}(s_t)\Big)\bigg] \\ &= \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} \bigg[\sum_{t=0}^\infin \gamma^t \Big(r(s_t,a_t) + \gamma V^{\pi_\theta}(s_{t+1}) - V^{\pi_{\theta}}(s_t)\Big)\bigg] \\ \end{aligned} J(θ′)−J(θ)=Es0[Vπθ′(s0)]−Es0[Vπθ(s0)]=Eτ∼pθ′(τ)[t=0∑∞γtr(st,at)]+Eτ∼pθ′(τ)[t=0∑∞γt(γVπθ(st+1)−Vπθ(st))]=Eτ∼pθ′(τ)[t=0∑∞γt(r(st,at)+γVπθ(st+1)−Vπθ(st))]
将时序差分残差定义为优势函数AAA:
=Eτ∼pθ′(τ)[∑t=0∞γtAπθ(st,at)]=∑t=0∞γtEst∼Ptπθ′Eat∼πθ′(⋅∣st)[Aπθ(st,at)]=11−γEs∼νπθ′Ea∼πθ′(⋅∣s)[Aπθ(s,a)]\begin{aligned} &= \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} \bigg[\sum_{t=0}^\infin \gamma^t A^{\pi_\theta}(s_t,a_t)\bigg] \\ &= \sum_{t=0}^\infin \gamma^t \mathbb{E}_{s_t \sim P_t^{\pi_{\theta'}}} \mathbb{E}_{a_t \sim \pi_{\theta'}(\cdot|s_t)} [A^{\pi_\theta}(s_t,a_t)] \\ &= \dfrac{1}{1-\gamma} \mathbb{E}_{s \sim \nu^{\pi_{\theta'}}} \mathbb{E}_{a \sim \pi_{\theta'}(\cdot|s)} [A^{\pi_\theta}(s,a)] \\ \end{aligned} =Eτ∼pθ′(τ)[t=0∑∞γtAπθ(st,at)]=t=0∑∞γtEst∼Ptπθ′Eat∼πθ′(⋅∣st)[Aπθ(st,at)]=1−γ1Es∼νπθ′Ea∼πθ′(⋅∣s)[Aπθ(s,a)]
最后一个等号的成立运用到了状态访问分布的定义:νπ(s)=(1−γ)∑t=0∞(1−γ)γtPtπ(s)\displaystyle \nu^\pi(s)=(1-\gamma)\sum_{t=0}^\infin (1-\gamma)\gamma^tP_t^\pi(s)νπ(s)=(1−γ)t=0∑∞(1−γ)γtPtπ(s),所以只要我们能找到一个新策略,使得Es∼νπθ′Ea∼πθ′(⋅∣s)[Aπθ(s,a)]≥0\mathbb{E}_{s \sim \nu^{\pi_{\theta'}}} \mathbb{E}_{a \sim \pi_{\theta'}(\cdot|s)} [A^{\pi_\theta}(s,a)] \ge 0Es∼νπθ′Ea∼πθ′(⋅∣s)[Aπθ(s,a)]≥0,就能保证策略性能单调递增,即J(θ′)≥J(θ)J(\theta') \ge J(\theta)J(θ′)≥J(θ)。
但是直接求解该式是非常困难的,因为πθ′\pi_{\theta'}πθ′是我们需要求解的策略,但我们又要用它来收集样本。(我们只是先求了一个πθ′\pi_{\theta'}πθ′,然后用之前的数据判断他好不好,不可能说拿他进行一轮采样再来判断,采样一次的成本太大了,而且这一般不是最优策略,显然更新要好多轮的,一直重新采样,可想而知时间开销多大)把所有可能的新策略都拿来收集数据,然后判断哪个策略满足上述条件的做法显然是不现实的。于是 TRPO 做了一步近似操作,对状态访问分布进行了相应处理。具体而言,忽略两个策略之间的状态访问分布变化,直接采用旧的策略πθ\pi_\thetaπθ的状态分布,定义如下替代优化目标:
J(θ′)≈Lθ(θ′)=J(θ)+11−γEs∼νπθEa∼πθ′(⋅∣s)[Aπθ(s,a)]J(\theta') \approx L_\theta(\theta') = J(\theta) + \dfrac{1}{1-\gamma} \mathbb{E}_{s \sim \nu^{\pi_{\theta}}} \mathbb{E}_{a \sim \pi_{\theta'}(\cdot|s)} [A^{\pi_\theta}(s,a)] J(θ′)≈Lθ(θ′)=J(θ)+1−γ1Es∼νπθEa∼πθ′(⋅∣s)[Aπθ(s,a)]
当新旧策略非常接近时,状态访问分布变化很小,这么近似是合理的。其中,动作仍然用新策略πθ′\pi_{\theta'}πθ′采样得到(这样我们只需用PolicyNet算一次就完成采样了),我们可以用重要性采样对动作分布进行处理:
Lθ(θ′)=J(θ)+11−γEs∼νπθEa∼πθ′(⋅∣s)[Aπθ(s,a)]=J(θ)+11−γEs∼νπθ[∑a∈Aπθ′(a∣s)⋅Aπθ(s,a)]=J(θ)+11−γEs∼νπθ[∑a∈Aπθ′(a∣s)⋅πθ(a∣s)πθ(a∣s)⋅Aπθ(s,a)]=J(θ)+11−γEs∼νπθ[∑a∈Aπθ(a∣s)⋅(πθ′(a∣s)πθ(a∣s)Aπθ(s,a))]=J(θ)+Es∼νπθEa∼πθ(⋅∣s)[πθ′(a∣s)πθ(a∣s)Aπθ(s,a)]\begin{aligned} L_\theta(\theta') &= J(\theta) + \dfrac{1}{1-\gamma} \mathbb{E}_{s \sim \nu^{\pi_{\theta}}} \mathbb{E}_{a \sim \pi_{\theta'}(\cdot|s)} [A^{\pi_\theta}(s,a)]\\ &= J(\theta) + \dfrac{1}{1-\gamma} \mathbb{E}_{s \sim \nu^{\pi_{\theta}}} \Big[\sum_{a \in \mathcal{A}} \pi_{\theta'}(a|s) \cdot A^{\pi_\theta}(s,a)\Big]\\ &= J(\theta) + \dfrac{1}{1-\gamma} \mathbb{E}_{s \sim \nu^{\pi_{\theta}}} \Big[\sum_{a \in \mathcal{A}} \pi_{\theta'}(a|s) \cdot \dfrac{\pi_{\theta}(a|s)}{\pi_{\theta}(a|s)} \cdot A^{\pi_\theta}(s,a)\Big]\\ &= J(\theta) + \dfrac{1}{1-\gamma} \mathbb{E}_{s \sim \nu^{\pi_{\theta}}} \bigg[\sum_{a \in \mathcal{A}} \pi_{\theta}(a|s) \cdot \Big( \dfrac{\pi_{\theta'}(a|s)}{\pi_{\theta}(a|s)} A^{\pi_\theta}(s,a) \Big)\bigg]\\ &= J(\theta) + \mathbb{E}_{s \sim \nu^{\pi_{\theta}}} \mathbb{E}_{a \sim \pi_{\theta}(\cdot|s)} \bigg[ \dfrac{\pi_{\theta'}(a|s)}{\pi_{\theta}(a|s)} A^{\pi_\theta}(s,a)\bigg] \\ \end{aligned} Lθ(θ′)=J(θ)+1−γ1Es∼νπθEa∼πθ′(⋅∣s)[Aπθ(s,a)]=J(θ)+1−γ1Es∼νπθ[a∈A∑πθ′(a∣s)⋅Aπθ(s,a)]=J(θ)+1−γ1Es∼νπθ[a∈A∑πθ′(a∣s)⋅πθ(a∣s)πθ(a∣s)⋅Aπθ(s,a)]=J(θ)+1−γ1Es∼νπθ[a∈A∑πθ(a∣s)⋅(πθ(a∣s)πθ′(a∣s)Aπθ(s,a))]=J(θ)+Es∼νπθEa∼πθ(⋅∣s)[πθ(a∣s)πθ′(a∣s)Aπθ(s,a)]
这样,我们就可以基于旧策略πθ\pi_\thetaπθ已经采样出的数据来估计并优化新策略πθ′\pi_{\theta'}πθ′了。为了保证新旧策略足够接近,TRPO 使用了库尔贝克-莱布勒(Kullback-Leibler,KL)散度来衡量策略之间的距离,并给出了整体的优化公式:
maxθ′Lθ(θ′)s.t. Es∼νπθk[DKL(πθk(⋅∣s),πθ′(⋅∣s))]≤δ\begin{aligned} & \underset{\theta'}{\max} L_\theta(\theta')\\ & \text{s.t. } \mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}} \Big[ D_{KL}\Big(\pi_{\theta_k}(\cdot|s), \pi_{\theta'}(\cdot|s)\Big) \Big]\le\delta \end{aligned} θ′maxLθ(θ′)s.t. Es∼νπθk[DKL(πθk(⋅∣s),πθ′(⋅∣s))]≤δ
这里的不等式约束定义了策略空间中的一个 KL 球,被称为信任区域。在这个区域中,可以认为当前学习策略和环境交互的状态分布与上一轮策略最后采样的状态分布一致,进而可以基于一步行动的重要性采样方法使当前学习策略稳定提升。TRPO 背后的原理如图 11-1 所示。
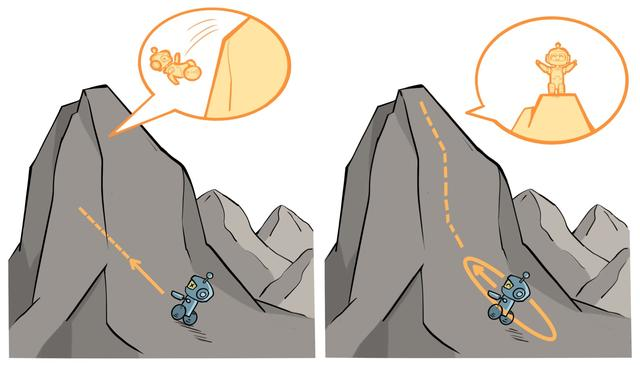
图11-1 TRPO原理示意图
左图表示当完全不设置信任区域时,策略的梯度更新可能导致策略的性能骤降;右图表示当设置了信任区域时,可以保证每次策略的梯度更新都能来带性能的提升。
11.3 近似求解
直接求解上式带约束的优化问题比较麻烦,TRPO 在其具体实现中做了一步近似操作来快速求解。为方便起见,我们在接下来的式子中用θk\theta_kθk代替之前的θ\thetaθ,表示这是第kkk次迭代之后的策略。首先对目标函数和约束在θk\theta_kθk进行泰勒展开,分别用 1 阶、2 阶进行近似:
Es∼νπθkEa∼πθk(⋅∣s)[πθ′(a∣s)πθk(a∣s)Aπθk(s,a)]≈gT(θ′−θk)\mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}} \mathbb{E}_{a \sim \pi_{\theta_k}(\cdot|s)} \bigg[ \dfrac{\pi_{\theta'}(a|s)}{\pi_{\theta_k}(a|s)} A^{\pi_{\theta_k}}(s,a)\bigg] \approx g^T(\theta' - \theta_k) Es∼νπθkEa∼πθk(⋅∣s)[πθk(a∣s)πθ′(a∣s)Aπθk(s,a)]≈gT(θ′−θk)
Es∼νπθk[DKL(πθk(⋅∣s),πθ′(⋅∣s))]≈12(θ′−θk)TH(θ′−θk)\mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}} \Big[ D_{KL}\Big(\pi_{\theta_k}(\cdot|s), \pi_{\theta'}(\cdot|s)\Big) \Big] \approx \dfrac{1}{2} (\theta' - \theta_k)^T H (\theta'-\theta_k) Es∼νπθk[DKL(πθk(⋅∣s),πθ′(⋅∣s))]≈21(θ′−θk)TH(θ′−θk)
其中g=∇θ′Es∼νπθkEa∼πθk(⋅∣s)[πθ′(a∣s)πθk(a∣s)Aπθk(s,a)]g=\nabla_{\theta'}\mathbb{E}_{s\sim\nu^{\pi_{\theta_k}}} \mathbb{E}_{a\sim\pi_{\theta_k}(\cdot|s)}\Big[\dfrac{\pi_{\theta'}(a|s)}{\pi_{\theta_k}(a|s)} A^{\pi_{\theta_k}}(s,a)\Big]g=∇θ′Es∼νπθkEa∼πθk(⋅∣s)[πθk(a∣s)πθ′(a∣s)Aπθk(s,a)],表示目标函数的梯度,H=H[Es∼νπθk[DKL(πθk(⋅∣s),πθ′(⋅∣s))]]H = \mathbf{H}\Big[\mathbb{E}_{s \sim \nu^{\pi_{\theta_k}}} \Big[D_{KL}\Big(\pi_{\theta_k}(\cdot|s), \pi_{\theta'}(\cdot|s)\Big)\Big]\Big]H=H[Es∼νπθk[DKL(πθk(⋅∣s),πθ′(⋅∣s))]]表示策略之间平均 KL 距离的黑塞矩阵(Hessian matrix)。
于是我们的优化目标变成了:
θk+1=arg maxθ′gT(θ′−θk)s.t. 12(θ′−θk)TH(θ′−θk)≤δ\begin{aligned} & \theta_{k+1} = \argmax_{\theta'} g^T(\theta' - \theta_k)\\ &\text{s.t. } \dfrac{1}{2} (\theta' - \theta_k)^T H (\theta'-\theta_k) \le \delta \end{aligned} θk+1=θ′argmaxgT(θ′−θk)s.t. 21(θ′−θk)TH(θ′−θk)≤δ
此时,我们可以用卡罗需-库恩-塔克(Karush-Kuhn-Tucker,KKT)条件直接导出上述问题的解:
θk+1=θk+2δgTH−1gH−1g\theta_{k+1} = \theta_k + \sqrt{\dfrac{2\delta}{g^T H^{-1} g}} H^{-1}g θk+1=θk+gTH−1g2δH−1g
证明
推导过程如下,根据KKT条件,可以得到以下结论:
首先修改优化问题为求最小值问题:
θk+1=−arg minθ′gT(θ′−θk)s.t. 12(θ′−θk)TH(θ′−θk)≤δ\begin{aligned} & \theta_{k+1} = - \argmin_{\theta'} g^T(\theta' - \theta_k)\\ &\text{s.t. } \dfrac{1}{2} (\theta' - \theta_k)^T H (\theta'-\theta_k) \le \delta \end{aligned} θk+1=−θ′argmingT(θ′−θk)s.t. 21(θ′−θk)TH(θ′−θk)≤δ
如果λ>0\lambda > 0λ>0,则有12(θ′−θk)TH(θ′−θk)=δ\dfrac{1}{2} (\theta' - \theta_k)^T H (\theta'-\theta_k) = \delta21(θ′−θk)TH(θ′−θk)=δ,即等式约束处于严格约束状态,此时Stationarity条件可以简化为:
∇θ′[−gT(θ′−θk)+λ(12(θ′−θk)TH(θ′−θk)−δ)]=0−g+λH(θ′−θk)=0θ′=θk+1λH−1g\begin{aligned} \nabla_{\theta'} \Big[-g^T(\theta' - \theta_k) + \lambda \Big( \dfrac{1}{2} (\theta' - \theta_k)^T H (\theta'-\theta_k) - \delta \Big) \Big] &= 0\\ -g + \lambda H (\theta'-\theta_k) &= 0 \\ \theta' &= \theta_k + \dfrac{1}{\lambda} H^{-1} g \end{aligned} ∇θ′[−gT(θ′−θk)+λ(21(θ′−θk)TH(θ′−θk)−δ)]−g+λH(θ′−θk)θ′=0=0=θk+λ1H−1g
将上式代入等式约束中,得到:
δ=12(1λH−1g)TH(1λH−1g)δ=12λ2gTH−1gλ=gTH−1g2δ\begin{aligned} \delta &= \dfrac{1}{2} (\dfrac{1}{\lambda} H^{-1}g)^T H (\dfrac{1}{\lambda} H^{-1}g)\\ \delta &= \dfrac{1}{2\lambda^2} g^T{H^{-1}}g\\ \lambda &= \sqrt{\dfrac{g^TH^{-1}g}{2\delta}} \end{aligned} δδλ=21(λ1H−1g)TH(λ1H−1g)=2λ21gTH−1g=2δgTH−1g
回代到 θ′\theta'θ′ 的表达式中:
θ′=θk+1λH−1g=θk+2δgTH−1gH−1g\theta' = \theta_k + \dfrac{1}{\lambda} H^{-1} g = \theta_k + \sqrt{\dfrac{2\delta}{g^TH^{-1}g}} H^{-1} g θ′=θk+λ1H−1g=θk+gTH−1g2δH−1g
如果λ=0\lambda = 0λ=0,则有12(θ′−θk)TH(θ′−θk)<δ\dfrac{1}{2} (\theta' - \theta_k)^T H (\theta'-\theta_k) < \delta21(θ′−θk)TH(θ′−θk)<δ,即等式约束处于松弛状态。此时,Stationarity条件可以简化为:
∇θ′[−gT(θ′−θk)+λ(12(θ′−θk)TH(θ′−θk)−δ)]=0gT=0\begin{aligned} \nabla_{\theta'} \Big[-g^T(\theta' - \theta_k) + \lambda \Big( \dfrac{1}{2} (\theta' - \theta_k)^T H (\theta'-\theta_k) - \delta \Big) \Big] &= 0\\ g^T &= 0 \end{aligned} ∇θ′[−gT(θ′−θk)+λ(21(θ′−θk)TH(θ′−θk)−δ)]gT=0=0
此时,最优解可以在不等式约束的边界处取到,综上有:
θk+1=θk+2δgTH−1gH−1g\theta_{k+1} = \theta_k + \sqrt{\dfrac{2\delta}{g^T H^{-1} g}} H^{-1}g θk+1=θk+gTH−1g2δH−1g
得证。
11.4 共轭梯度
一般来说,用神经网络表示的策略函数的参数数量都是成千上万的,计算和存储黑塞矩阵的逆矩阵HHH会耗费大量的内存资源和时间。TRPO 通过共轭梯度法(conjugate gradient method)回避了这个问题。易观察到更新公式中 θk+1=θk+2δgTH−1gH−1g\theta_{k+1} = \theta_k + \sqrt{\dfrac{2\delta}{g^T H^{-1} g}} H^{-1}gθk+1=θk+gTH−1g2δH−1g 由向量 H−1gH^{-1} gH−1g 和标量 2δgTH−1g\sqrt{\dfrac{2\delta}{g^T H^{-1} g}}gTH−1g2δ 共同组成。通过换元法,把向量换成x=H−1gx=H^{-1}gx=H−1g表示参数更新方向。假设满足 KL 距离约束的参数更新时的最大步长为β\betaβ,于是,根据 KL 距离约束条件,有12(βx)TH(βx)=δ\dfrac{1}{2}(\beta x)^TH(\beta x) = \delta21(βx)TH(βx)=δ。求解β\betaβ:
12(βx)TH(βx)=δβ22xTHx=δβ2=2δxTHxβ=2δxTHx\begin{aligned} \dfrac{1}{2}(\beta x)^TH(\beta x) &= \delta \\ \dfrac{\beta^2}{2}x^T H x &= \delta \\ \beta^2&= \dfrac{2\delta}{x^T H x} \\ \beta &= \sqrt{\dfrac{2\delta}{x^T H x}} \\ \end{aligned} 21(βx)TH(βx)2β2xTHxβ2β=δ=δ=xTHx2δ=xTHx2δ
得到β=2δxTHx\beta = \sqrt{\dfrac{2\delta}{x^THx}}β=xTHx2δ。因此,此时参数更新方式为
θk+1=θk+2δxTHxx\theta_{k+1} = \theta_k + \sqrt{\dfrac{2\delta}{x^THx}}x θk+1=θk+xTHx2δx
因此,只要可以直接计算x=H−1gx=H^{-1}gx=H−1g,就可以根据该式更新参数,问题转化为解Hx=gHx=gHx=g。实际上HHH为对称正定矩阵,所以我们可以使用共轭梯度法来求解。共轭梯度法的具体流程如下:
- 初始化r0=g−Hx0r_0=g-Hx_0r0=g−Hx0,p0=r0p_0=r_0p0=r0,x0=0x_0=0x0=0
- for k=0→Nk=0 \rightarrow Nk=0→N do:
- 计算步长:αk=rkTrkpkTHpk\alpha_k=\dfrac{r_k^T r_k}{p_k^T H p_k}αk=pkTHpkrkTrk
- 更新当前解:xk+1=xk+αkpkx_{k+1} = x_k + \alpha_k p_kxk+1=xk+αkpk
- 更新残差:rk+1=rk−αkHpkr_{k+1} = r_k - \alpha_k H p_krk+1=rk−αkHpk
- 如果rk+1Trk+1r_{k+1}^Tr_{k+1}rk+1Trk+1非常小,则退出循环
- 计算新搜索方向的权重系数:βk=rk+1Trk+1rkTrk\beta_k = \dfrac{r_{k+1}^Tr_{k+1}}{r_k^Tr_k}βk=rkTrkrk+1Trk+1
- 计算新的搜索方向:pk+1=rk+1+βkpkp_{k+1}=r_{k+1} + \beta_kp_kpk+1=rk+1+βkpk
- end for
- 输出xN+1x_{N+1}xN+1
在共轭梯度运算过程中,直接计算αk\alpha_kαk和rk+1r_{k+1}rk+1需要计算和存储海森矩阵HHH。为了避免这种大矩阵的出现,我们只计算HxH_xHx向量,而不直接计算和存储HHH矩阵。这样做比较容易,因为对于任意的列向量vvv,容易验证:
Hv=∇θ((∇θ(DKLνπθk(πθk,πθ′)))T)v=∇θ((∇θ(DKLνπθk(πθk,πθ′)))Tv)Hv = \nabla_\theta \bigg( \Big(\nabla_\theta (D_{KL}^{\nu^{\pi_{\theta_k}}}(\pi_{\theta_k, \pi_{\theta'}}))\Big)^T \bigg)v = \nabla_\theta \bigg( \Big(\nabla_\theta (D_{KL}^{\nu^{\pi_{\theta_k}}}(\pi_{\theta_k, \pi_{\theta'}}))\Big)^T v \bigg) Hv=∇θ((∇θ(DKLνπθk(πθk,πθ′)))T)v=∇θ((∇θ(DKLνπθk(πθk,πθ′)))Tv)
即先用梯度和向量vvv点乘后计算梯度。
11.5 线性搜索
由于 TRPO 算法用到了泰勒展开的 1 阶和 2 阶近似,这并非精准求解,因此,θ′\theta'θ′可能未必比θk\theta_kθk好,或未必能满足 KL 散度限制。TRPO 在每次迭代的最后进行一次线性搜索(Line Search),以确保找到满足条件。具体来说,就是找到一个最小的非负整数iii,使得按照
θk+1=θk+αi2δxTHxx\theta_{k+1} = \theta_k + \alpha^i\sqrt{\dfrac{2\delta}{x^THx}}x θk+1=θk+αixTHx2δx
求出的θk+1\theta_{k+1}θk+1依然满足最初的 KL 散度限制,并且确实能够提升目标函数LθkL_{\theta_k}Lθk,这其中α∈(0,1)\alpha\in(0,1)α∈(0,1)是一个决定线性搜索长度的超参数。
至此,我们已经基本上清楚了 TRPO 算法的大致过程,它具体的算法流程如下:
- 初始化策略网络参数θ\thetaθ,价值网络参数ω\omegaω
- for 序列e=1→Ee=1\rightarrow Ee=1→E do:
- 用当前策略πθ\pi_\thetaπθ采样轨迹{s1,a1,r1,s2,a2,r2,⋯ }\{s_1,a_1,r_1,s_2,a_2,r_2, \cdots\}{s1,a1,r1,s2,a2,r2,⋯}
- 根据收集到的数据和价值网络估计每个状态动作对的优势A(st,at)A(s_t,a_t)A(st,at)
- 计算策略目标函数的梯度ggg
- 用共轭梯度法计算x=H−1gx=H^{-1}gx=H−1g
- 用线性搜索找到一个iii值,并更新策略网络参数θk+1=θk+αi2δxTHxx\theta_{k+1} = \theta_k + \alpha^i\sqrt{\dfrac{2\delta}{x^THx}}xθk+1=θk+αixTHx2δx,其中i∈{1,2,⋯ ,K}i\in\{1,2,\cdots,K\}i∈{1,2,⋯,K}为能 提升- 策略并满足 KL 距离限制的最小整数
- 更新价值网络参数(与 Actor-Critic 中的更新方法相同)
- end for
11.6 广义优势估计
从 11.5 节中,我们尚未得知如何估计优势函数AAA。目前比较常用的一种方法为广义优势估计(Generalized Advantage Estimation,GAE),接下来我们简单介绍一下 GAE 的做法。首先,用δt=rt+γV(st+1)−V(st)\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)δt=rt+γV(st+1)−V(st)表示时序差分误差,其中VVV是一个已经学习的状态价值函数。于是,根据多步时序差分的思想,有:
At(1)=δt=−V(st)+rt+γV(st+1)At(2)=δt+γδt+1=−V(st)+rt+γrt+1+γ2V(st+2)At(2)=δt+γδt+1+γ2δt+2=−V(st)+rt+γrt+1+γ2rt+2+γ3V(st+3)⋮At(k)=∑l=0k−1γlδt+l=−V(st)+rt+γrt+1+⋯+γk−1rt+k−1+γkV(st+)\begin{aligned} &&A_t^{(1)} &= \delta_t &&= -V(s_t) + r_t + \gamma V(s_{t+1}) \\ &&A_t^{(2)} &= \delta_t + \gamma\delta_{t+1} &&= -V(s_t) + r_t + \gamma r_{t+1} + \gamma^2 V(s_{t+2}) \\ &&A_t^{(2)} &= \delta_t + \gamma\delta_{t+1} + \gamma^2\delta_{t+2} &&= -V(s_t) + r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \gamma^3 V(s_{t+3})\\ &&&&&\vdots\\ &&A_t^{(k)} &= \sum_{l=0}^{k-1} \gamma^l\delta_{t+l} &&= -V(s_t) + r_t + \gamma r_{t+1} + \cdots + \gamma^{k-1}r_{t+k-1} + \gamma^kV(s_{t+}) \\ \end{aligned} At(1)At(2)At(2)At(k)=δt=δt+γδt+1=δt+γδt+1+γ2δt+2=l=0∑k−1γlδt+l=−V(st)+rt+γV(st+1)=−V(st)+rt+γrt+1+γ2V(st+2)=−V(st)+rt+γrt+1+γ2rt+2+γ3V(st+3)⋮=−V(st)+rt+γrt+1+⋯+γk−1rt+k−1+γkV(st+)
然后,GAE 将这些不同步数的优势估计进行指数加权平均:
AtGAE=(1−λ)(At(1)+λAt(2)+λ2At(3)+⋯ )=(1−λ)(δt+λ(δt+γδt+1)+λ2(δt+γδt+1+γ2δt+2)+⋯ )=(1−λ)(δ(1+λ+λ2+⋯ )+γδt+1(λ+λ2+λ3+⋯ )+γ2δt+2(λ2+λ3+λ4+⋯ )+⋯ )=(1−λ)(δt11−λ+γδt+1λ1−λ+γ2δt+2λ21−λ+⋯)=δt+γλδt+1+(γλ)2δt+2+⋯=∑l=0∞(γλ)lδt+l\begin{aligned} A_t^{GAE} &= (1-\lambda)(A_t^{(1)} + \lambda A_t^{(2)} + \lambda^2 A_t^{(3)} + \cdots)\\ &= (1-\lambda)(\delta_t + \lambda (\delta_t + \gamma \delta_{t+1}) + \lambda^2 (\delta_t + \gamma\delta_{t+1} + \gamma^2\delta_{t+2}) + \cdots)\\ &= (1-\lambda)(\delta(1+\lambda+\lambda^2 +\cdots) + \gamma\delta_{t+1}(\lambda + \lambda^2 + \lambda^3 + \cdots) + \gamma^2\delta_{t+2}(\lambda^2 + \lambda^3 + \lambda^4 + \cdots) + \cdots)\\ &= (1-\lambda) \bigg(\delta_t \dfrac{1}{1-\lambda} + \gamma\delta_{t+1}\dfrac{\lambda}{1-\lambda} + \gamma^2\delta_{t+2}\dfrac{\lambda^2}{1-\lambda} + \cdots\bigg)\\ &= \delta_{t} + \gamma\lambda \delta_{t+1} + (\gamma\lambda)^2 \delta_{t+2} + \cdots\\ &= \sum_{l=0}^\infin (\gamma\lambda)^l \delta_{t+l} \end{aligned} AtGAE=(1−λ)(At(1)+λAt(2)+λ2At(3)+⋯)=(1−λ)(δt+λ(δt+γδt+1)+λ2(δt+γδt+1+γ2δt+2)+⋯)=(1−λ)(δ(1+λ+λ2+⋯)+γδt+1(λ+λ2+λ3+⋯)+γ2δt+2(λ2+λ3+λ4+⋯)+⋯)=(1−λ)(δt1−λ1+γδt+11−λλ+γ2δt+21−λλ2+⋯)=δt+γλδt+1+(γλ)2δt+2+⋯=l=0∑∞(γλ)lδt+l
有递推式:
AtGAE=δt+γλδt+1+(γλ)2δt+2+⋯AtGAE=δt+γλ(δt+1+γλδt+2+⋯)AtGAE=δt+γλAt+1GAE\begin{aligned} A_{t}^{GAE} &= \delta_{t} + \gamma\lambda \delta_{t+1} + (\gamma\lambda)^2 \delta_{t+2} + \cdots\\ A_{t}^{GAE} &= \delta_{t} + \gamma\lambda\bigg( \delta_{t+1} + \gamma\lambda \delta_{t+2} + \cdots \bigg)\\ A_{t}^{GAE} &= \delta_{t} + \gamma\lambda A_{t+1}^{GAE}\\ \end{aligned} AtGAEAtGAEAtGAE=δt+γλδt+1+(γλ)2δt+2+⋯=δt+γλ(δt+1+γλδt+2+⋯)=δt+γλAt+1GAE
其中,λ∈[0,1]\lambda\in[0,1]λ∈[0,1]是在 GAE 中额外引入的一个超参数。当λ=0\lambda=0λ=0时,AtGAE=δt=rt+γV(st+1)−V(st)A_t^{GAE}=\delta_t=r_t+\gamma V(s_{t+1})-V(s_t)AtGAE=δt=rt+γV(st+1)−V(st),也即是仅仅只看一步差分得到的优势;当λ=1\lambda=1λ=1时,AtGAE=∑l=0∞γlδt+l=∑l=0∞γlrt+l−V(st)\displaystyle A_t^{GAE}=\sum_{l=0}^\infin \gamma^l \delta_{t+l} = \sum_{l=0}^\infin \gamma^l r_{t+l} - V(s_t)AtGAE=l=0∑∞γlδt+l=l=0∑∞γlrt+l−V(st),则是看每一步差分得到优势的完全平均值。
下面一段是 GAE 的代码,给定γ,λ\gamma,\lambdaγ,λ以及每个时间步的δt\delta_tδt之后,我们可以根据公式直接进行优势估计。
def compute_advantage(gamma, lmbda, td_delta):
td_delta = td_delta.detach().numpy()
advantage_list = []
advantage = 0.0
for delta in td_delta[::-1]:
advantage = gamma * lmbda * advantage + delta
advantage_list.append(advantage)
advantage_list.reverse()
return torch.tensor(advantage_list, dtype=torch.float)
11.7 TRPO 代码实践
本节将使用支持与离散和连续两种动作交互的环境来进行 TRPO 的实验。我们使用的第一个环境是车杆(CartPole),第二个环境是倒立摆(Inverted Pendulum)。
首先导入一些必要的库。
import torch
import numpy as np
import gym
import matplotlib.pyplot as plt
import torch.nn.functional as F
import rl_utils
import copy
然后定义策略网络和价值网络(与 Actor-Critic 算法一样)。
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
class ValueNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim):
super(ValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
class TRPO:
""" TRPO算法 """
def __init__(
self,
hidden_dim,
state_space,
action_space,
lmbda,
kl_constraint,
alpha,
critic_lr,
gamma,
device
):
state_dim = state_space.shape[0]
action_dim = action_space.n
# 策略网络参数不需要优化器更新
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
self.lmbda = lmbda # GAE参数
self.kl_constraint = kl_constraint # KL距离最大限制
self.alpha = alpha # 线性搜索参数
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def hessian_matrix_vector_product(self, states, old_action_dists, vector):
# 计算黑塞矩阵和一个向量的乘积
# 计算新模型actor根据states输出的动作状态分布
new_action_dists = torch.distributions.Categorical(self.actor(states))
# 计算新旧分布的平均KL距离
kl = torch.mean(torch.distributions.kl.kl_divergence(old_action_dists,new_action_dists))
# kl距离求一阶导
kl_grad = torch.autograd.grad(kl, self.actor.parameters(), create_graph=True)
kl_grad_vector = torch.cat([grad.view(-1) for grad in kl_grad])
# KL距离的梯度先和向量进行点积运算(之前提到的Trick,可以不用存储二阶导的黑塞矩阵)
kl_grad_vector_product = torch.dot(kl_grad_vector, vector)
# 求二阶导
grad2 = torch.autograd.grad(kl_grad_vector_product, self.actor.parameters())
grad2_vector = torch.cat([grad.view(-1) for grad in grad2])
# 返回答案
return grad2_vector
def conjugate_gradient(self, grad, states, old_action_dists): # 共轭梯度法求解方程
x = torch.zeros_like(grad) # 初始化 x = 0
r = grad.clone() # r = g - Hx = g - 0 = 0
p = grad.clone() # p = r
rdotr = torch.dot(r, r)
for i in range(10): # 共轭梯度主循环
# 计算Hp
Hp = self.hessian_matrix_vector_product(states, old_action_dists, p)
alpha = rdotr / torch.dot(p, Hp) # alpha = (r^T r) / (p^T H p)
x += alpha * p # x = x + alpha * p
r -= alpha * Hp # r = r - alpha * H *p
new_rdotr = torch.dot(r, r)
if new_rdotr < 1e-10: # 收敛就提前结束
break
beta = new_rdotr / rdotr
p = r + beta * p
rdotr = new_rdotr
return x
def compute_surrogate_obj(self, states, actions, advantage, old_log_probs, actor): # 计算策略目标
# 计算 log(\pi_\theta (actions|states))
log_probs = torch.log(actor(states).gather(1, actions))
# 重要性采样
ratio = torch.exp(log_probs - old_log_probs)
# 相乘获得目标函数
return torch.mean(ratio * advantage)
def line_search(self, states, actions, advantage, old_log_probs, old_action_dists, max_vec): # 线性搜索
# 取出旧参数
old_para = torch.nn.utils.convert_parameters.parameters_to_vector(self.actor.parameters())
# 计算旧目标函数
old_obj = self.compute_surrogate_obj(states, actions, advantage, old_log_probs, self.actor)
for i in range(15): # 线性搜索主循环
# 计算alpha指数系数
coef = self.alpha**i
# 根据线性搜索章节的公式,更新出新的参数 theta_{k+1}
new_para = old_para + coef * max_vec
# 深拷贝一个new_actor,用于比较更新参数前后的模型表现
new_actor = copy.deepcopy(self.actor)
# 用新参数更新新模型
torch.nn.utils.convert_parameters.vector_to_parameters(new_para, new_actor.parameters())
# 用新模型求出动作分布
new_action_dists = torch.distributions.Categorical(new_actor(states))
# 计算两个模型求出的动作分布的KL散度
kl_div = torch.mean(torch.distributions.kl.kl_divergence(old_action_dists, new_action_dists))
# 计算新参数模型的surrogate目标
new_obj = self.compute_surrogate_obj(states, actions, advantage, old_log_probs, new_actor)
# 如果目标函数是增长的(性能更好)且KL散度满足要求,则进行参数更新
if new_obj > old_obj and kl_div < self.kl_constraint:
return new_para
return old_para
def policy_learn(self, states, actions,old_action_dists, old_log_probs, advantage): # 更新策略函数
# surrogate obj 目标函数
surrogate_obj = self.compute_surrogate_obj(states,actions, advantage, old_log_probs, self.actor)
# 用泰勒展开到一阶,用一阶导数来近似该目标函数,之后的目标函数就是 g^T (theta' - theta)
grads = torch.autograd.grad(surrogate_obj, self.actor.parameters())
# grads是parameters形状的tuple,把他展成一个一维向量,便于后续操作
g = torch.cat([grad.view(-1) for grad in grads]).detach()
# 用共轭梯度法计算x = H^(-1)g
descent_direction = self.conjugate_gradient(g, states, old_action_dists)
# 计算黑塞矩阵和一维向量的乘积:Hx
Hd = self.hessian_matrix_vector_product(states, old_action_dists, descent_direction)
# 计算KKT条件导出的答案
max_coef = torch.sqrt(2 * self.kl_constraint / (torch.dot(descent_direction, Hd) + 1e-8))
# 用线性搜索找出最有答案
new_para = self.line_search(states, actions, advantage, old_log_probs, old_action_dists, descent_direction * max_coef)
# 用线性搜索后的参数更新策略
torch.nn.utils.convert_parameters.vector_to_parameters(new_para, self.actor.parameters())
def update(self, transition_dict):
# 取出回放经验池采样样本的各类数据
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
# 计算td_target和td_delta
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones)
td_delta = td_target - self.critic(states)
# 更新价值函数
critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
# 更新策略函数
# 优势函数用广义优势函数GAE
advantage = compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device)
# 计算就模型的 log(\pi_\theta (actions|states))
old_log_probs = torch.log(self.actor(states).gather(1, actions)).detach()
# 计算旧模型对于states计算的离散动作分布
old_action_dists = torch.distributions.Categorical(self.actor(states).detach())
# 看似在线性搜索以前,actor始终没变过,你认为不需要区分old和new
# 这里要这么做,实际是为了去计算图,以便于求导的时候不会对这部分求,这样old就始终是old了
self.policy_learn(states, actions, old_action_dists, old_log_probs, advantage)
接下来在车杆环境中训练 TRPO,并将结果可视化。
num_episodes = 500
hidden_dim = 128
gamma = 0.98
lmbda = 0.95
critic_lr = 1e-2
kl_constraint = 0.0005
alpha = 0.5
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
agent = TRPO(hidden_dim, env.observation_space, env.action_space, lmbda, kl_constraint, alpha, critic_lr, gamma, device)
return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('TRPO on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('TRPO on {}'.format(env_name))
plt.show()
Iteration 0: 100%|██████████| 50/50 [00:03<00:00, 15.71it/s, episode=50, return=139.200]
Iteration 1: 100%|██████████| 50/50 [00:03<00:00, 13.08it/s, episode=100, return=150.500]
Iteration 2: 100%|██████████| 50/50 [00:04<00:00, 11.57it/s, episode=150, return=184.000]
Iteration 3: 100%|██████████| 50/50 [00:06<00:00, 7.60it/s, episode=200, return=183.600]
Iteration 4: 100%|██████████| 50/50 [00:06<00:00, 7.17it/s, episode=250, return=183.500]
Iteration 5: 100%|██████████| 50/50 [00:04<00:00, 10.91it/s, episode=300, return=193.700]
Iteration 6: 100%|██████████| 50/50 [00:04<00:00, 10.70it/s, episode=350, return=199.500]
Iteration 7: 100%|██████████| 50/50 [00:04<00:00, 10.89it/s, episode=400, return=200.000]
Iteration 8: 100%|██████████| 50/50 [00:04<00:00, 10.80it/s, episode=450, return=200.000]
Iteration 9: 100%|██████████| 50/50 [00:04<00:00, 11.09it/s, episode=500, return=200.000]
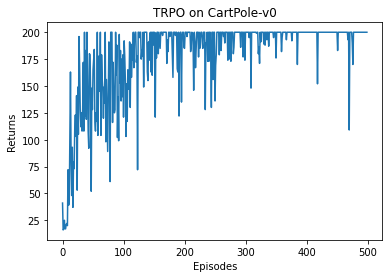
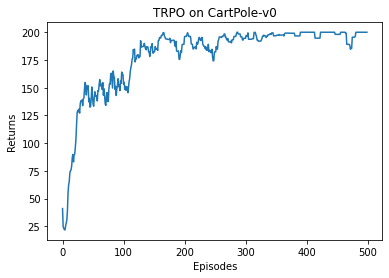
TRPO 在车杆环境中很快收敛,展现了十分优秀的性能效果。
接下来我们尝试倒立摆环境,由于它是与连续动作交互的环境,我们需要对上面的代码做一定的修改。对于策略网络,因为环境是连续动作的,所以策略网络分别输出表示动作分布的高斯分布的均值和标准差。
class PolicyNetContinuous(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc_mu = torch.nn.Linear(hidden_dim, action_dim)
self.fc_std = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
mu = 2.0 * torch.tanh(self.fc_mu(x))
std = F.softplus(self.fc_std(x))
return mu, std # 高斯分布的均值和标准差
class TRPOContinuous:
""" 处理连续动作的TRPO算法 """
def __init__(
self,
hidden_dim,
state_space,
action_space,
lmbda,
kl_constraint,
alpha,
critic_lr,
gamma,
device
):
state_dim = state_space.shape[0]
action_dim = action_space.shape[0]
self.actor = PolicyNetContinuous(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
self.lmbda = lmbda
self.kl_constraint = kl_constraint
self.alpha = alpha
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
mu, std = self.actor(state)
action_dist = torch.distributions.Normal(mu, std)
action = action_dist.sample()
return [action.item()]
def hessian_matrix_vector_product(self, states, old_action_dists, vector, damping=0.1):
mu, std = self.actor(states)
new_action_dists = torch.distributions.Normal(mu, std)
kl = torch.mean(torch.distributions.kl.kl_divergence(old_action_dists, new_action_dists))
kl_grad = torch.autograd.grad(kl, self.actor.parameters(), create_graph=True)
kl_grad_vector = torch.cat([grad.view(-1) for grad in kl_grad])
kl_grad_vector_product = torch.dot(kl_grad_vector, vector)
grad2 = torch.autograd.grad(kl_grad_vector_product, self.actor.parameters())
grad2_vector = torch.cat([grad.contiguous().view(-1) for grad in grad2])
return grad2_vector + damping * vector
def conjugate_gradient(self, grad, states, old_action_dists):
x = torch.zeros_like(grad)
r = grad.clone()
p = grad.clone()
rdotr = torch.dot(r, r)
for i in range(10):
Hp = self.hessian_matrix_vector_product(states, old_action_dists, p)
alpha = rdotr / torch.dot(p, Hp)
x += alpha * p
r -= alpha * Hp
new_rdotr = torch.dot(r, r)
if new_rdotr < 1e-10:
break
beta = new_rdotr / rdotr
p = r + beta * p
rdotr = new_rdotr
return x
def compute_surrogate_obj(self, states, actions, advantage, old_log_probs, actor):
mu, std = actor(states)
action_dists = torch.distributions.Normal(mu, std)
log_probs = action_dists.log_prob(actions)
ratio = torch.exp(log_probs - old_log_probs)
return torch.mean(ratio * advantage)
def line_search(self, states, actions, advantage, old_log_probs, old_action_dists, max_vec):
old_para = torch.nn.utils.convert_parameters.parameters_to_vector(self.actor.parameters())
old_obj = self.compute_surrogate_obj(states, actions, advantage, old_log_probs, self.actor)
for i in range(15):
coef = self.alpha ** i
new_para = old_para + coef * max_vec
new_actor = copy.deepcopy(self.actor)
torch.nn.utils.convert_parameters.vector_to_parameters(new_para, new_actor.parameters())
mu, std = new_actor(states)
new_action_dists = torch.distributions.Normal(mu, std)
kl_div = torch.mean(torch.distributions.kl.kl_divergence(old_action_dists, new_action_dists))
new_obj = self.compute_surrogate_obj(states, actions, advantage, old_log_probs, new_actor)
if new_obj > old_obj and kl_div < self.kl_constraint:
return new_para
return old_para
def policy_learn(self, states, actions, old_action_dists, old_log_probs, advantage):
surrogate_obj = self.compute_surrogate_obj(states, actions, advantage, old_log_probs, self.actor)
grads = torch.autograd.grad(surrogate_obj, self.actor.parameters())
obj_grad = torch.cat([grad.view(-1) for grad in grads]).detach()
descent_direction = self.conjugate_gradient(obj_grad, states, old_action_dists)
Hd = self.hessian_matrix_vector_product(states, old_action_dists, descent_direction)
max_coef = torch.sqrt(2 * self.kl_constraint / (torch.dot(descent_direction, Hd) + 1e-8))
new_para = self.line_search(states, actions, advantage, old_log_probs, old_action_dists, descent_direction * max_coef)
torch.nn.utils.convert_parameters.vector_to_parameters(new_para, self.actor.parameters())
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = (rewards + 8.0) / 8.0 # 对奖励进行修改,方便训练
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones)
td_delta = td_target - self.critic(states)
advantage = compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device)
mu, std = self.actor(states)
old_action_dists = torch.distributions.Normal(mu.detach(), std.detach())
old_log_probs = old_action_dists.log_prob(actions)
critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
self.policy_learn(states, actions, old_action_dists, old_log_probs, advantage)
接下来我们在倒立摆环境下训练连续动作版本的 TRPO 算法,并观测它的训练性能曲线。本段代码的完整运行需要一定的时间。
num_episodes = 2000
hidden_dim = 128
gamma = 0.9
lmbda = 0.9
critic_lr = 1e-2
kl_constraint = 0.00005
alpha = 0.5
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'Pendulum-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
agent = TRPOContinuous(hidden_dim, env.observation_space, env.action_space, lmbda, kl_constraint, alpha, critic_lr, gamma, device)
return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('TRPO on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('TRPO on {}'.format(env_name))
plt.show()
Iteration 0: 100%|██████████| 200/200 [00:23<00:00, 8.63it/s, episode=200, return=-1181.390]
Iteration 1: 100%|██████████| 200/200 [00:23<00:00, 8.68it/s, episode=400, return=-994.876]
Iteration 2: 100%|██████████| 200/200 [00:23<00:00, 8.39it/s, episode=600, return=-888.498]
Iteration 3: 100%|██████████| 200/200 [00:23<00:00, 8.69it/s, episode=800, return=-848.329]
Iteration 4: 100%|██████████| 200/200 [00:23<00:00, 8.68it/s, episode=1000, return=-772.392]
Iteration 5: 100%|██████████| 200/200 [00:22<00:00, 8.72it/s, episode=1200, return=-611.870]
Iteration 6: 100%|██████████| 200/200 [00:23<00:00, 8.62it/s, episode=1400, return=-397.705]
Iteration 7: 100%|██████████| 200/200 [00:23<00:00, 8.68it/s, episode=1600, return=-268.498]
Iteration 8: 100%|██████████| 200/200 [00:23<00:00, 8.61it/s, episode=1800, return=-408.976]
Iteration 9: 100%|██████████| 200/200 [00:23<00:00, 8.49it/s, episode=2000, return=-296.363]
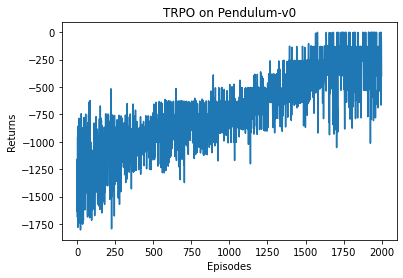
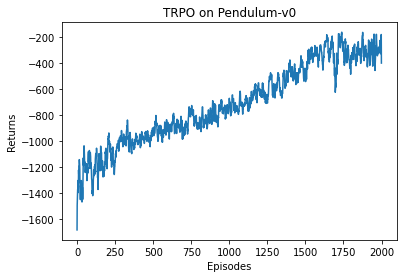
用 TRPO 在与连续动作交互的倒立摆环境中能够取得非常不错的效果,这说明 TRPO 中的信任区域优化方法在离散和连续动作空间都能有效工作。
11.8 总结
本章讲解了 TRPO 算法,并分别在离散动作和连续动作交互的环境中进行了实验。TRPO 算法属于在线策略学习方法,每次策略训练仅使用上一轮策略采样的数据,是基于策略的深度强化学习算法中十分有代表性的工作之一。直觉性地理解,TRPO 给出的观点是:由于策略的改变导致数据分布的改变,这大大影响深度模型实现的策略网络的学习效果,所以通过划定一个可信任的策略学习区域,保证策略学习的稳定性和有效性。
TRPO 算法是比较难掌握的一种强化学习算法,需要较好的数学基础。读者若在学习过程中遇到困难,可自行查阅相关资料。TRPO 有一些后续工作,其中最著名的当属 PPO,我们将在第 12 章进行介绍。
11.9 参考文献
[1] SCHULMAN J, LEVINE S, ABBEEL P, et al. Trust region policy optimization [C]// International conference on machine learning, PMLR, 2015:1889-1897.
[2] SHAM K M. A natural policy gradient [C]// Advances in neural information processing systems 2001: 14.
[3] SCHULMAN J, MORITZ P, LEVINE S, et al. High-dimensional continuous control using generalized advantage estimation [C]// International conference on learning representation, 2016.
12 PPO 算法
12.1 简介
第 11 章介绍的 TRPO 算法在很多场景上的应用都很成功,但是我们也发现它的计算过程非常复杂,每一步更新的运算量非常大。于是,TRPO 算法的改进版——PPO 算法在 2017 年被提出,PPO 基于 TRPO 的思想,但是其算法实现更加简单。并且大量的实验结果表明,与 TRPO 相比,PPO 能学习得一样好(甚至更快),这使得 PPO 成为非常流行的强化学习算法。如果我们想要尝试在一个新的环境中使用强化学习算法,那么 PPO 就属于可以首先尝试的算法。
回忆一下 TRPO 的优化目标:
maxθEs∼νπθkEa∼πθk(⋅∣s)[πθ(a∣s)πθk(a∣s)Aπθk(s,a)]s.t. Es∼νπθk[DKL(πθk(⋅∣s)∣∣πθ(⋅∣s))]≤δ\begin{aligned} & \max_{\theta} \mathbb{E}_{s\sim \nu^{\pi_{\theta_k}}} \mathbb{E}_{a\sim \pi_{\theta_k}(\cdot|s)} \bigg[ \dfrac{\pi_{\theta}(a|s)}{\pi_{\theta_k}(a|s)} A^{\pi_{\theta_k}}(s,a) \bigg]\\ & \text{s.t. } \mathbb{E}_{s\sim \nu^{\pi_{\theta_k}}} \bigg[ D_{KL}\Big(\pi_{\theta_k}(\cdot|s) || \pi_{\theta}(\cdot|s)\Big) \bigg] \le \delta \end{aligned} θmaxEs∼νπθkEa∼πθk(⋅∣s)[πθk(a∣s)πθ(a∣s)Aπθk(s,a)]s.t. Es∼νπθk[DKL(πθk(⋅∣s)∣∣πθ(⋅∣s))]≤δ
TRPO 使用泰勒展开近似、共轭梯度、线性搜索等方法直接求解。PPO 的优化目标与 TRPO 相同,但 PPO 用了一些相对简单的方法来求解。具体来说,PPO 有两种形式,一是 PPO-惩罚,二是 PPO-截断,我们接下来对这两种形式进行介绍。
12.2 PPO-惩罚
PPO-惩罚(PPO-Penalty)用拉格朗日乘数法直接将 KL 散度的限制放进了目标函数中,这就变成了一个无约束的优化问题,在迭代的过程中不断更新 KL 散度前的系数。即:
arg maxθEs∼νπθkEa∼πθk(⋅∣s)[πθ(a∣s)πθk(a∣s)Aπθk(s,a)−βDKL[πθk(⋅∣s),πθ(⋅∣s)]]\underset{\theta}{\argmax} \mathbb{E}_{s\sim \nu^{\pi_{\theta_k}}} \mathbb{E}_{a\sim \pi_{\theta_k}(\cdot|s)} \bigg[ \dfrac{\pi_{\theta}(a|s)}{\pi_{\theta_k}(a|s)} A^{\pi_{\theta_k}}(s,a) - \beta D_{KL}\Big[\pi_{\theta_k}(\cdot|s), \pi_{\theta}(\cdot|s)\Big] \bigg] θargmaxEs∼νπθkEa∼πθk(⋅∣s)[πθk(a∣s)πθ(a∣s)Aπθk(s,a)−βDKL[πθk(⋅∣s),πθ(⋅∣s)]]
令dk=DKLνπθk(πθk,πθ)d_k=D_{KL}^{\nu^{\pi_{\theta_k}}}(\pi_{\theta_k}, \pi_\theta)dk=DKLνπθk(πθk,πθ), β\betaβ的更新规则如下:
- 如果,那么dk<δ1.5d_k < \dfrac{\delta}{1.5}dk<1.5δ,那么βk+1=βk2\beta_{k+1} = \dfrac{\beta_k}{2}βk+1=2βk
- 如果dk>δ×1.5d_k > \delta \times 1.5dk>δ×1.5,那么βk+1=βk×2\beta_{k+1} = \beta_k \times 2βk+1=βk×2
- 否则βk+1=βk\beta_{k+1}=\beta_kβk+1=βk
其中,δ\deltaδ是事先设定的一个超参数,用于限制学习策略和之前一轮策略的差距。
12.3 PPO-截断
PPO 的另一种形式 PPO-截断(PPO-Clip)更加直接,它在目标函数中进行限制,以保证新的参数和旧的参数的差距不会太大,即:
arg maxθEs∼νπθkEa∼πθk(⋅∣s)[min(πθ(a∣s)πθk(a∣s)Aπθk(s,a),clip(πθ(a∣s)πθk(a∣s),1−ϵ,1+ϵ)Aπθk(s,a))]\argmax_{\theta} \mathbb{E}_{s\sim\nu^{\pi_{\theta_k}}} \mathbb{E}_{a\sim\pi_{\theta_k}(\cdot|s)} \bigg[ \min \bigg( \dfrac{\pi_{\theta}(a|s)}{\pi_{\theta_k}(a|s)} A^{\pi_{\theta_k}}(s,a), \operatorname{clip}\Big( \dfrac{\pi_{\theta}(a|s)}{\pi_{\theta_k}(a|s)}, 1-\epsilon, 1+\epsilon \Big)A^{\pi_{\theta_k}}(s,a) \bigg) \bigg] θargmaxEs∼νπθkEa∼πθk(⋅∣s)[min(πθk(a∣s)πθ(a∣s)Aπθk(s,a),clip(πθk(a∣s)πθ(a∣s),1−ϵ,1+ϵ)Aπθk(s,a))]
其中clip(x,l,r):=max(min(x,r),l)\operatorname{clip}(x,l,r):=\max(\min(x,r),l)clip(x,l,r):=max(min(x,r),l),即把xxx限制在[l,r][l,r][l,r]内。上式中ϵ\epsilonϵ是一个超参数,表示进行截断(clip)的范围。
如果Aπθk(s,a)>0A^{\pi_{\theta_k}}(s,a) > 0Aπθk(s,a)>0,说明这个动作的价值高于平均,最大化这个式子会增大πθ(a∣s)πθk(a∣s)\dfrac{\pi_{\theta}(a|s)}{\pi_{\theta_k}(a|s)}πθk(a∣s)πθ(a∣s),但不会让其超过1+ϵ1+\epsilon1+ϵ。反之,如果Aπθk(s,a)<0A^{\pi_{\theta_k}}(s,a) < 0Aπθk(s,a)<0,最大化这个式子会减小πθ(a∣s)πθk(a∣s)\dfrac{\pi_{\theta}(a|s)}{\pi_{\theta_k}(a|s)}πθk(a∣s)πθ(a∣s),但不会让其超过1−ϵ1-\epsilon1−ϵ。如图 12-1 所示。
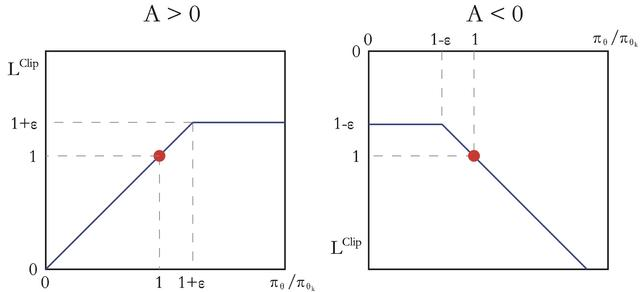
12.4 PPO 代码实践
与 TRPO 相同,我们仍然在车杆和倒立摆两个环境中测试 PPO 算法。大量实验表明,PPO-截断总是比 PPO-惩罚表现得更好。因此下面我们专注于 PPO-截断的代码实现。
首先导入一些必要的库,并定义策略网络和价值网络。
import gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
import rl_utils
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
class ValueNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim):
super(ValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
class PPO:
''' PPO算法,采用截断方式 '''
def __init__(
self,
state_dim,
hidden_dim,
action_dim,
actor_lr,
critic_lr,
lmbda,
epochs,
eps,
gamma,
device
):
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device)
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
self.lmbda = lmbda
self.epochs = epochs # 一条序列的数据用来训练轮数
self.eps = eps # PPO中截断范围的参数
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones)
td_delta = td_target - self.critic(states)
advantage = rl_utils.compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device)
old_log_probs = torch.log(self.actor(states).gather(1, actions)).detach()
for _ in range(self.epochs):
log_probs = torch.log(self.actor(states).gather(1, actions))
ratio = torch.exp(log_probs - old_log_probs)
surr1 = ratio * advantage
surr2 = torch.clamp(ratio, 1 - self.eps, 1 + self.eps) * advantage # 截断
actor_loss = torch.mean(-torch.min(surr1, surr2)) # PPO损失函数
critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward()
critic_loss.backward()
self.actor_optimizer.step()
self.critic_optimizer.step()
接下来在车杆环境中训练 PPO 算法。
actor_lr = 1e-3
critic_lr = 1e-2
num_episodes = 500
hidden_dim = 128
gamma = 0.98
lmbda = 0.95
epochs = 10
eps = 0.2
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = PPO(
state_dim,
hidden_dim,
action_dim,
actor_lr,
critic_lr,
lmbda,
epochs,
eps,
gamma,
device
)
return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
Iteration 0: 100%|██████████| 50/50 [00:02<00:00, 19.41it/s, episode=50, return=183.200]
Iteration 1: 100%|██████████| 50/50 [00:03<00:00, 13.49it/s, episode=100, return=184.900]
Iteration 2: 100%|██████████| 50/50 [00:03<00:00, 12.64it/s, episode=150, return=200.000]
Iteration 3: 100%|██████████| 50/50 [00:03<00:00, 12.64it/s, episode=200, return=200.000]
Iteration 4: 100%|██████████| 50/50 [00:03<00:00, 12.81it/s, episode=250, return=200.000]
Iteration 5: 100%|██████████| 50/50 [00:03<00:00, 12.63it/s, episode=300, return=200.000]
Iteration 6: 100%|██████████| 50/50 [00:03<00:00, 12.83it/s, episode=350, return=200.000]
Iteration 7: 100%|██████████| 50/50 [00:03<00:00, 12.58it/s, episode=400, return=200.000]
Iteration 8: 100%|██████████| 50/50 [00:03<00:00, 12.78it/s, episode=450, return=200.000]
Iteration 9: 100%|██████████| 50/50 [00:03<00:00, 12.59it/s, episode=500, return=187.200]
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('PPO on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('PPO on {}'.format(env_name))
plt.show()
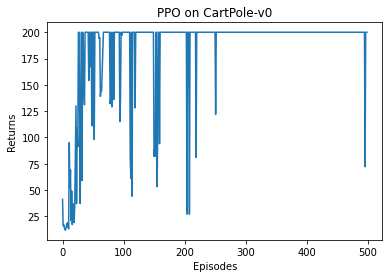
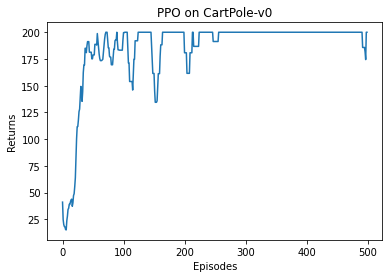
倒立摆是与连续动作交互的环境,同 TRPO 算法一样,我们做一些修改,让策略网络输出连续动作高斯分布(Gaussian distribution)的均值和标准差。后续的连续动作则在该高斯分布中采样得到。
class PolicyNetContinuous(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc_mu = torch.nn.Linear(hidden_dim, action_dim)
self.fc_std = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
mu = 2.0 * torch.tanh(self.fc_mu(x))
std = F.softplus(self.fc_std(x))
return mu, std
class PPOContinuous:
''' 处理连续动作的PPO算法 '''
def __init__(
self,
state_dim,
hidden_dim,
action_dim,
actor_lr,
critic_lr,
lmbda,
epochs,
eps,
gamma,
device
):
self.actor = PolicyNetContinuous(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device)
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
self.lmbda = lmbda
self.epochs = epochs
self.eps = eps
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
mu, sigma = self.actor(state)
action_dist = torch.distributions.Normal(mu, sigma)
action = action_dist.sample()
return [action.item()]
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = (rewards + 8.0) / 8.0 # 和TRPO一样,对奖励进行修改,方便训练
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones)
td_delta = td_target - self.critic(states)
advantage = rl_utils.compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device)
mu, std = self.actor(states)
action_dists = torch.distributions.Normal(mu.detach(), std.detach())
# 动作是正态分布
old_log_probs = action_dists.log_prob(actions)
for _ in range(self.epochs):
mu, std = self.actor(states)
action_dists = torch.distributions.Normal(mu, std)
log_probs = action_dists.log_prob(actions)
ratio = torch.exp(log_probs - old_log_probs)
surr1 = ratio * advantage
surr2 = torch.clamp(ratio, 1 - self.eps, 1 + self.eps) * advantage
actor_loss = torch.mean(-torch.min(surr1, surr2))
critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach()))
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward()
critic_loss.backward()
self.actor_optimizer.step()
self.critic_optimizer.step()
创建环境Pendulum-v0,并设定随机数种子以便重复实现。接下来我们在倒立摆环境中训练 PPO 算法。
actor_lr = 1e-4
critic_lr = 5e-3
num_episodes = 2000
hidden_dim = 128
gamma = 0.9
lmbda = 0.9
epochs = 10
eps = 0.2
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'Pendulum-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0] # 连续动作空间
agent = PPOContinuous(
state_dim,
hidden_dim,
action_dim,
actor_lr,
critic_lr,
lmbda,
epochs,
eps,
gamma,
device
)
return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
Iteration 0: 100%|██████████| 200/200 [00:22<00:00, 9.02it/s, episode=200, return=-1000.354]
Iteration 1: 100%|██████████| 200/200 [00:22<00:00, 8.78it/s, episode=400, return=-922.780]
Iteration 2: 100%|██████████| 200/200 [00:20<00:00, 9.63it/s, episode=600, return=-483.957]
Iteration 3: 100%|██████████| 200/200 [00:20<00:00, 9.80it/s, episode=800, return=-472.933]
Iteration 4: 100%|██████████| 200/200 [00:20<00:00, 9.54it/s, episode=1000, return=-327.589]
Iteration 5: 100%|██████████| 200/200 [00:20<00:00, 9.63it/s, episode=1200, return=-426.262]
Iteration 6: 100%|██████████| 200/200 [00:20<00:00, 9.73it/s, episode=1400, return=-224.806]
Iteration 7: 100%|██████████| 200/200 [00:21<00:00, 9.49it/s, episode=1600, return=-279.722]
Iteration 8: 100%|██████████| 200/200 [00:20<00:00, 9.62it/s, episode=1800, return=-428.538]
Iteration 9: 100%|██████████| 200/200 [00:20<00:00, 9.81it/s, episode=2000, return=-235.771]
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('PPO on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 21)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('PPO on {}'.format(env_name))
plt.show()
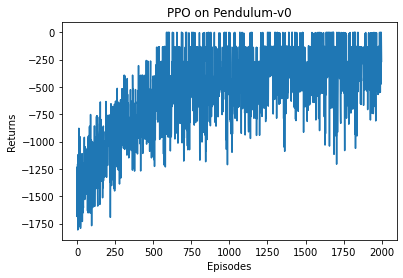

12.5 总结
PPO 是 TRPO 的一种改进算法,它在实现上简化了 TRPO 中的复杂计算,并且它在实验中的性能大多数情况下会比 TRPO 更好,因此目前常被用作一种常用的基准算法。需要注意的是,TRPO 和 PPO 都属于在线策略学习算法,即使优化目标中包含重要性采样的过程,但其只是用到了上一轮策略的数据,而不是过去所有策略的数据。
PPO 是 TRPO 的第一作者 John Schulman 从加州大学伯克利分校博士毕业后在 OpenAI 公司研究出来的。通过对 TRPO 计算方式的改进,PPO 成为了最受关注的深度强化学习算法之一,并且其论文的引用量也超越了 TRPO。
12.6 参考文献
[1] SCHULMAN J, FILIP W, DHARIWAL P, et al. Proximal policy optimization algorithms [J]. Machine Learning, 2017.
13 DDPG 算法
13.1 简介
之前的章节介绍了基于策略梯度的算法 REINFORCE、Actor-Critic 以及两个改进算法——TRPO 和 PPO。这类算法有一个共同的特点:它们都是在线策略算法,这意味着它们的样本效率(sample efficiency)比较低。我们回忆一下 DQN 算法,DQN 算法直接估计最优函数 Q,可以做到离线策略学习,但是它只能处理动作空间有限的环境,这是因为它需要从所有动作中挑选一个QQQ值最大的动作。如果动作个数是无限的,虽然我们可以像 8.3 节一样,将动作空间离散化,但这比较粗糙,无法精细控制。那有没有办法可以用类似的思想来处理动作空间无限的环境并且使用的是离线策略算法呢?本章要讲解的深度确定性策略梯度(deep deterministic policy gradient,DDPG)算法就是如此,它构造一个确定性策略,用梯度上升的方法来最大化QQQ值。DDPG 也属于一种 Actor-Critic 算法。我们之前学习的 REINFORCE、TRPO 和 PPO 学习随机性策略,而本章的 DDPG 则学习一个确定性策略。
13.2 DDPG 算法
之前我们学习的策略是随机性的,可以表示为a∼πθ(⋅∣s)a \sim\pi_{\theta}(\cdot|s)a∼πθ(⋅∣s);而如果策略是确定性的,则可以记为a=μθ(s)a=\mu_\theta(s)a=μθ(s)。与策略梯度定理类似,我们可以推导出确定性策略梯度定理(deterministic policy gradient theorem):
∇θJ(πθ)=Es∼νπβ[∇θμθ(s)∇aQωμ(s,a)∣a=μθ(s)]\nabla_\theta J(\pi_\theta) = \mathbb{E}_{s\sim\nu^{\pi_\beta}} \Big[ \nabla_\theta \mu_\theta (s) \nabla_a Q_\omega^\mu (s,a) | a=\mu_\theta(s) \Big] ∇θJ(πθ)=Es∼νπβ[∇θμθ(s)∇aQωμ(s,a)∣a=μθ(s)]
其中,πβ\pi_\betaπβ是用来收集数据的行为策略。我们可以这样理解这个定理:假设现在已经有函数QQQ,给定一个状态sss,但由于现在动作空间是无限的,无法通过遍历所有动作来得到值最大的动作QQQ,因此我们想用策略μ\muμ找到使Q(s,a)Q(s,a)Q(s,a)值最大的动作aaa,即μ(s)=arg maxaQ(s,a)\mu(s) = \underset{a}{\argmax}Q(s,a)μ(s)=aargmaxQ(s,a)。此时,QQQ就是 Critic,μ\muμ就是 Actor,这是一个 Actor-Critic 的框架,如图 13-1 所示。
那如何得到这个μ\muμ呢?首先用QQQ对μθ\mu_\thetaμθ求导∇θQ(s,μθ(s))\nabla_\theta Q(s,\mu_\theta(s))∇θQ(s,μθ(s)),其中会用到梯度的链式法则,先对aaa求导,再对θ\thetaθ求导。然后通过梯度上升的方法来最大化函数QQQ,得到QQQ值最大的动作。具体的推导过程可参见 13.5 节。

图13-1 DDPG 中的 Actor 网络和 Critic 网络,以倒立摆环境为例
下面我们来看一下 DDPG 算法的细节。DDPG 要用到444个神经网络,其中 Actor 和 Critic 各用一个网络,此外它们都各自有一个目标网络。至于为什么需要目标网络,读者可以回到第 7 章去看 DQN 中的介绍。DDPG 中 Actor 也需要目标网络因为目标网络也会被用来计算目标QQQ值。DDPG 中目标网络的更新与 DQN 中略有不同:在 DQN 中,每隔一段时间将QQQ网络直接复制给目标QQQ网络;而在 DDPG 中,目标QQQ网络的更新采取的是一种软更新的方式,即让目标QQQ网络缓慢更新,逐渐接近QQQ网络,其公式为:
ω−←τω+(1−τ)ω−\omega^{-} \leftarrow \tau\omega + (1 - \tau)\omega^{-} ω−←τω+(1−τ)ω−
通常τ\tauτ是一个比较小的数,当τ=1\tau=1τ=1时,就和 DQN 的更新方式一致了。而目标μ\muμ网络也使用这种软更新的方式。
另外,由于函数QQQ存在QQQ值过高估计的问题,DDPG 采用了 Double DQN 中的技术来更新QQQ网络。但是,由于 DDPG 采用的是确定性策略,它本身的探索仍然十分有限。回忆一下 DQN 算法,它的探索主要由ε-贪婪策略的行为策略产生。同样作为一种离线策略的算法,DDPG 在行为策略上引入一个随机噪声N\mathcal{N}N来进行探索。我们来看一下 DDPG 的具体算法流程吧!
- 随机噪声可以用N\mathcal{N}N来表示,用随机的网络参数ω\omegaω和θ\thetaθ分别初始化 Critic 网络Qω(s,a)Q_\omega(s,a)Qω(s,a)和 Actor 网络μθ(s)\mu_\theta(s)μθ(s)
- 复制相同的参数ω−←ω\omega^{-}\leftarrow\omegaω−←ω和θ−←θ\theta^{-}\leftarrow\thetaθ−←θ,分别初始化目标网络Qω−Q_{\omega^{-}}Qω−和μθ−\mu_{\theta^{-}}μθ−
- 初始化经验回放池RRR
- for 序列e=1→Ee=1\rightarrow Ee=1→E do :
- 初始化随机过程N\mathcal{N}N用于动作探索
- 获取环境初始状态s1s_1s1
- for时间步t=1→Tt=1\rightarrow Tt=1→T do :
- 根据当前策略和噪声选择动作at=μθ(st)+Na_t = \mu_\theta(s_t) + \mathcal{N}at=μθ(st)+N
- 执行动作ata_tat,获得奖励rtr_trt,环境状态变为st+1s_{t+1}st+1
- 将(st,at,rt,st+1)(s_t,a_t,r_t,s_{t+1})(st,at,rt,st+1)存储进回放池RRR
- 从RRR中采样NNN个元组{(si,ai,ri,si+1)}i=1,2,⋯ ,N\Big\{ (s_i,a_i,r_i,s_{i+1}) \Big\}_{i=1,2,\cdots,N}{(si,ai,ri,si+1)}i=1,2,⋯,N
- 对每个元组,用目标网络计算yi=ri+γQω−(si+1,μθ−(si+1))y_i=r_i+\gamma Q_{\omega^{-}}(s_{i+1},\mu_{\theta^{-}}(s_{i+1}))yi=ri+γQω−(si+1,μθ−(si+1))
- 最小化目标损失L=1N∑i=1N[yi−Qω(si,ai)]2\displaystyle L = \dfrac{1}{N}\sum_{i=1}^N \Big[ y_i - Q_{\omega}(s_i, a_i) \Big]^2L=N1i=1∑N[yi−Qω(si,ai)]2,以此更新当前 Critic 网络
- 计算采样的策略梯度,以此更新当前 Actor 网络:∇θJ≈1N∑i=1N∇θμθ(si)∇aQω(si,a)∣a=μθ(si)\nabla_\theta J \approx \dfrac{1}{N} \sum_{i=1}^N \nabla_\theta \mu_\theta(s_i) \nabla_a Q_{\omega} (s_i, a)|_{a=\mu_\theta(s_i)} ∇θJ≈N1i=1∑N∇θμθ(si)∇aQω(si,a)∣a=μθ(si)
- 更新目标网络:ω−←τω+(1−τ)ω−θ−←τθ+(1−τ)θ−\begin{aligned} \omega^{-} &\leftarrow \tau\omega + (1-\tau)\omega^{-}\\ \theta^{-} &\leftarrow \tau\theta + (1 - \tau)\theta^{-} \end{aligned} ω−θ−←τω+(1−τ)ω−←τθ+(1−τ)θ−
- end for
- end for
13.3 DDPG 代码实践
下面我们以倒立摆环境为例,结合代码详细讲解 DDPG 的具体实现。
import random
import gym
import numpy as np
from tqdm import tqdm
import torch
from torch import nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
对于策略网络和价值网络,我们都采用只有一层隐藏层的神经网络。策略网络的输出层用正切函数(y=tanhxy=\tanh xy=tanhx)作为激活函数,这是因为正切函数的值域是[−1,1][-1, 1][−1,1],方便按比例调整成环境可以接受的动作范围。在 DDPG 中处理的是与连续动作交互的环境,QQQ网络的输入是状态和动作拼接后的向量,QQQ网络的输出是一个值,表示该状态动作对的价值。
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
self.action_bound = action_bound # action_bound是环境可以接受的动作最大值
def forward(self, x):
x = F.relu(self.fc1(x))
return torch.tanh(self.fc2(x)) * self.action_bound
class QValueNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(QValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
self.fc_out = torch.nn.Linear(hidden_dim, 1)
def forward(self, x, a):
cat = torch.cat([x, a], dim=1) # 拼接状态和动作
x = F.relu(self.fc1(cat))
x = F.relu(self.fc2(x))
return self.fc_out(x)
接下来是 DDPG 算法的主体部分。在用策略网络采取动作的时候,为了更好地探索,我们向动作中加入高斯噪声。在 DDPG 的原始论文中,添加的噪声符合奥恩斯坦-乌伦贝克(Ornstein-Uhlenbeck,OU)随机过程:
Δxt=θ(μ−xt−1)+σW\Delta x_t = \theta (\mu - x_{t-1}) + \sigma W Δxt=θ(μ−xt−1)+σW
其中,μ\muμ是均值,WWW是符合布朗运动的随机噪声,θ\thetaθ和σ\sigmaσ是比例参数。可以看出,当xt−1x_{t-1}xt−1偏离均值时,xtx_txt的值会向均值靠拢。OU 随机过程的特点是在均值附近做出线性负反馈,并有额外的干扰项。OU 随机过程是与时间相关的,适用于有惯性的系统。在 DDPG 的实践中,不少地方仅使用正态分布的噪声。这里为了简单起见,同样使用正态分布的噪声,感兴趣的读者可以自行改为 OU 随机过程并观察效果。
class DDPG:
''' DDPG算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device):
self.actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
self.critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
self.target_actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
self.target_critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
# 初始化目标价值网络并设置和价值网络相同的参数
self.target_critic.load_state_dict(self.critic.state_dict())
# 初始化目标策略网络并设置和策略相同的参数
self.target_actor.load_state_dict(self.actor.state_dict())
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
self.sigma = sigma # 高斯噪声的标准差,均值直接设为0
self.tau = tau # 目标网络软更新参数
self.action_dim = action_dim
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.actor(state).item()
# 给动作添加噪声,增加探索
action = action + self.sigma * np.random.randn(self.action_dim)
return action
def soft_update(self, net, target_net):
for param_target, param in zip(target_net.parameters(), net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - self.tau) + param.data * self.tau)
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
next_q_values = self.target_critic(next_states, self.target_actor(next_states))
q_targets = rewards + self.gamma * next_q_values * (1 - dones)
critic_loss = torch.mean(F.mse_loss(self.critic(states, actions), q_targets))
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
actor_loss = -torch.mean(self.critic(states, self.actor(states)))
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
self.soft_update(self.actor, self.target_actor) # 软更新策略网络
self.soft_update(self.critic, self.target_critic) # 软更新价值网络
接下来我们在倒立摆环境中训练 DDPG,并绘制其性能曲线。
actor_lr = 3e-4
critic_lr = 3e-3
num_episodes = 200
hidden_dim = 64
gamma = 0.98
tau = 0.005 # 软更新参数
buffer_size = 10000
minimal_size = 1000
batch_size = 64
sigma = 0.01 # 高斯噪声标准差
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'Pendulum-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
action_bound = env.action_space.high[0] # 动作最大值
agent = DDPG(state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device)
return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size)
Iteration 0: 100%|██████████| 20/20 [00:11<00:00, 1.78it/s, episode=20, return=-1266.015]
Iteration 1: 100%|██████████| 20/20 [00:14<00:00, 1.39it/s, episode=40, return=-610.296]
Iteration 2: 100%|██████████| 20/20 [00:14<00:00, 1.37it/s, episode=60, return=-185.336]
Iteration 3: 100%|██████████| 20/20 [00:14<00:00, 1.36it/s, episode=80, return=-201.593]
Iteration 4: 100%|██████████| 20/20 [00:14<00:00, 1.37it/s, episode=100, return=-157.392]
Iteration 5: 100%|██████████| 20/20 [00:14<00:00, 1.39it/s, episode=120, return=-156.995]
Iteration 6: 100%|██████████| 20/20 [00:14<00:00, 1.39it/s, episode=140, return=-175.051]
Iteration 7: 100%|██████████| 20/20 [00:14<00:00, 1.36it/s, episode=160, return=-191.872]
Iteration 8: 100%|██████████| 20/20 [00:14<00:00, 1.38it/s, episode=180, return=-192.037]
Iteration 9: 100%|██████████| 20/20 [00:14<00:00, 1.36it/s, episode=200, return=-204.490]
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DDPG on {}'.format(env_name))
plt.show()
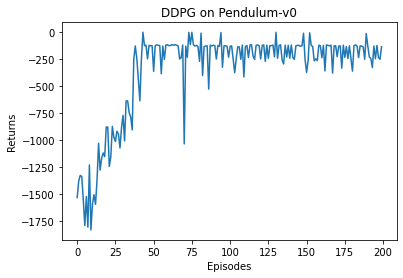

可以发现 DDPG 在倒立摆环境中表现出很不错的效果,其学习速度非常快,并且不需要太多样本。有兴趣的读者可以尝试自行调节超参数(例如用于探索的高斯噪声参数),观察训练结果的变化。
13.4 小结
本章讲解了深度确定性策略梯度算法(DDPG),它是面向连续动作空间的深度确定性策略训练的典型算法。相比于它的先期工作,即确定性梯度算法(DPG),DDPG 加入了目标网络和软更新的方法,这对深度模型构建的价值网络和策略网络的稳定学习起到了关键的作用。DDPG 算法也被引入了多智能体强化学习领域,催生了 MADDPG 算法,我们会在后续的章节中对此展开讨论。
13.5 扩展阅读:确定性策略梯度定理的证明
对于确定性策略μ\muμ,强化学习的目标函数可以写成期望的形式:
J(μθ)=∫Sνμθ(s)r(s,μθ(s))ds=Es∼νμθ[r(s,μθ(s))]J(\mu_\theta) = \int_{\mathcal{S}} \nu^{\mu_{\theta}}(s)r\Big(s,\mu_\theta(s)\Big)\mathrm{d} s = \mathbb{E}_{s\sim\nu^{\mu_\theta}}\Big[r\Big(s,\mu_\theta(s)\Big)\Big] J(μθ)=∫Sνμθ(s)r(s,μθ(s))ds=Es∼νμθ[r(s,μθ(s))]
其中,S\mathcal{S}S表示状态空间,ν\nuν是第 3 章介绍过的状态访问分布。下面的证明过程与策略梯度定理较为相似,可以对比阅读。
首先直接计算Vμθ(s)V^{\mu_\theta}(s)Vμθ(s)对θ\thetaθ的梯度。由于μθ\mu_\thetaμθ是确定性策略,因此Vμθ(s)=Qμθ(s,μθ(s))V^{\mu_\theta}(s) = Q^{\mu_\theta}(s,\mu_\theta(s))Vμθ(s)=Qμθ(s,μθ(s)),进而可以给出如下推导:
∇θVμθ(s)=∇θQμθ(s,μθ(s))=∇θ(r(s,μθ(s))+∫Sγp(s′∣s,μθ(s))Vμθ(s′)ds′)=∇θμθ(s)∇ar(s,a)∣a=μθ(s)+∇θ∫Sγp(s′∣s,μθ(s))Vμθ(s′)ds′=∇θμθ(s)∇ar(s,a)∣a=μθ(s)+∫Sγ(p(s′∣s,μθ(s))∇θVμθ(s′)+∇θμθ(s)∇ap(s′∣s,a)∣a=μθ(s)Vμθ(s′))ds′=∇θμθ(s)∇a(r(s,a)+∫Sγp(s′∣s,a)Vμθ(s′)ds′)∣a=μθ(s)+∫Sγp(s′∣s,μθ(s))∇θVμθ(s′)ds′=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫Sγp(s′∣s,μθ(s))∇θVμθ(s′)ds′\begin{aligned} \nabla_\theta V^{\mu_\theta}(s) &= \nabla_\theta Q^{\mu_\theta}(s,\mu_\theta(s)) \\ &= \nabla_\theta \bigg( r\Big(s,\mu_\theta(s)\Big) + \int_{\mathcal{S}} \gamma p\Big(s'|s,\mu_\theta(s)\Big)V^{\mu_\theta}(s')\mathrm{d}s' \bigg)\\ &= \nabla_\theta \mu_\theta (s) \nabla_a r(s,a)|_{a=\mu_\theta(s)} + \nabla_\theta \int_{\mathcal{S}} \gamma p\Big(s'|s, \mu_\theta(s)\Big) V^{\mu_\theta}(s')\mathrm{d}s'\\ &= \nabla_\theta \mu_\theta (s) \nabla_a r(s,a)|_{a=\mu_\theta(s)} + \int_{\mathcal{S}} \gamma \bigg( p\Big(s'|s, \mu_\theta(s)\Big) \nabla_\theta V^{\mu_\theta}(s') + \nabla_\theta \mu_\theta (s) \nabla_a p(s'|s, a)|_{a=\mu_\theta(s)} V^{\mu_\theta}(s')\bigg)\mathrm{d}s'\\ &= \nabla_\theta \mu_\theta (s) \nabla_a \bigg( r(s,a) + \int_{\mathcal{S}} \gamma p(s'|s,a) V^{\mu_\theta}(s')\mathrm{d}s' \bigg)|_{a=\mu_{\theta}(s)} + \int_{\mathcal{S}} \gamma p\Big(s'|s, \mu_\theta(s)\Big) \nabla_\theta V^{\mu_\theta}(s')\mathrm{d}s'\\ &= \nabla_\theta \mu_\theta (s) \nabla_a Q^{\mu_\theta}(s,a)|_{a=\mu_\theta(s)} + \int_{\mathcal{S}} \gamma p\Big(s'|s, \mu_\theta(s)\Big) \nabla_\theta V^{\mu_\theta}(s')\mathrm{d}s'\\ \end{aligned} ∇θVμθ(s)=∇θQμθ(s,μθ(s))=∇θ(r(s,μθ(s))+∫Sγp(s′∣s,μθ(s))Vμθ(s′)ds′)=∇θμθ(s)∇ar(s,a)∣a=μθ(s)+∇θ∫Sγp(s′∣s,μθ(s))Vμθ(s′)ds′=∇θμθ(s)∇ar(s,a)∣a=μθ(s)+∫Sγ(p(s′∣s,μθ(s))∇θVμθ(s′)+∇θμθ(s)∇ap(s′∣s,a)∣a=μθ(s)Vμθ(s′))ds′=∇θμθ(s)∇a(r(s,a)+∫Sγp(s′∣s,a)Vμθ(s′)ds′)∣a=μθ(s)+∫Sγp(s′∣s,μθ(s))∇θVμθ(s′)ds′=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫Sγp(s′∣s,μθ(s))∇θVμθ(s′)ds′
至此我们仅进行了简单的链式求导、合并同类项和代换,下面重点对等式右边的积分进行处理。积分中出现的∇θVμθ(s′)\nabla_\theta V^{\mu_\theta}(s')∇θVμθ(s′)项正是等式左边要计算的∇θVμθ(s)\nabla_\theta V^{\mu_\theta}(s)∇θVμθ(s)在状态s′s's′下的值,因此可以进行反复迭代:
∇θVμθ(s)=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫Sγp(s→s′,1,μθ)∇θVμθ(s′)ds′=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫Sγp(s→s′,1,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′+∫S(γp(s→s′,1,μθ)∫Sγp(s′→s′′,1,μθ)∇θVμθ(s′′)ds′′)ds′=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫Sγp(s→s′,1,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′+∫Sγ2p(s→s′,2,μθ)∇θVμθ(s′)ds′=⋯=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫S∑t=1∞γtp(s→s′,t,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′=∫S∑t=0∞γtp(s→s′,t,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′\begin{aligned} \nabla_\theta V^{\mu_\theta}(s) &= \nabla_\theta \mu_\theta (s) \nabla_a Q^{\mu_\theta}(s,a)|_{a=\mu_\theta(s)} + \int_{\mathcal{S}} \gamma p(s \rightarrow s', 1, \mu_\theta) \nabla_\theta V^{\mu_\theta}(s')\mathrm{d}s' \\ &= \nabla_\theta \mu_\theta (s) \nabla_a Q^{\mu_\theta}(s,a)|_{a=\mu_\theta(s)}\\ &+ \int_{\mathcal{S}} \gamma p(s \rightarrow s', 1, \mu_\theta) \nabla_\theta \mu_\theta(s') \nabla_a Q^{\mu_\theta}(s',a)|_{a=\mu_\theta(s')}\mathrm{d}s'\\ &+ \int_{\mathcal{S}} \bigg(\gamma p(s \rightarrow s', 1, \mu_\theta) \int_{\mathcal{S}}\gamma p(s' \rightarrow s'', 1, \mu_\theta)\nabla_\theta V^{\mu_\theta}(s'')\mathrm{d}s''\bigg)\mathrm{d}s'\\ &= \nabla_\theta \mu_\theta (s) \nabla_a Q^{\mu_\theta}(s,a)|_{a=\mu_\theta(s)}\\ &+ \int_{\mathcal{S}} \gamma p(s \rightarrow s', 1, \mu_\theta) \nabla_\theta \mu_\theta(s') \nabla_a Q^{\mu_\theta}(s',a)|_{a=\mu_\theta(s')}\mathrm{d}s'\\ &+ \int_{\mathcal{S}} \gamma^2 p(s \rightarrow s', 2, \mu_\theta) \nabla_\theta V^{\mu_\theta}(s')\mathrm{d}s'\\ &= \cdots \\ &= \nabla_\theta \mu_\theta (s) \nabla_a Q^{\mu_\theta}(s,a)|_{a=\mu_\theta(s)}\\ &+ \int_{\mathcal{S}} \sum_{t=1}^\infin \gamma^t p(s \rightarrow s', t, \mu_\theta) \nabla_\theta \mu_\theta(s') \nabla_a Q^{\mu_\theta}(s',a)|_{a=\mu_\theta(s')}\mathrm{d}s'\\ &= \int_{\mathcal{S}} \sum_{t=0}^\infin \gamma^t p(s \rightarrow s', t, \mu_\theta) \nabla_\theta \mu_\theta(s') \nabla_a Q^{\mu_\theta}(s',a)|_{a=\mu_\theta(s')}\mathrm{d}s'\\ \end{aligned} ∇θVμθ(s)=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫Sγp(s→s′,1,μθ)∇θVμθ(s′)ds′=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫Sγp(s→s′,1,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′+∫S(γp(s→s′,1,μθ)∫Sγp(s′→s′′,1,μθ)∇θVμθ(s′′)ds′′)ds′=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫Sγp(s→s′,1,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′+∫Sγ2p(s→s′,2,μθ)∇θVμθ(s′)ds′=⋯=∇θμθ(s)∇aQμθ(s,a)∣a=μθ(s)+∫St=1∑∞γtp(s→s′,t,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′=∫St=0∑∞γtp(s→s′,t,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′
这样就计算出了Vμθ(s)V^{\mu_\theta}(s)Vμθ(s)对θ\thetaθ的梯度。最终的优化目标累积回报函数J(μθ)J(\mu_\theta)J(μθ)的其中一种定义就是V(s)V(s)V(s)按照初始状态的分布ν0(s)\nu_0(s)ν0(s)对状态求期望:
J(μθ)=∫Sν0(s)Vμθ(s)dsJ(\mu_\theta) = \int_{\mathcal{S}} \nu_0 (s) V^{\mu_\theta}(s) \mathrm{d}s J(μθ)=∫Sν0(s)Vμθ(s)ds
计算J(μθ)J(\mu_\theta)J(μθ)对θ\thetaθ梯度并代入上面的结果,就得到
∇θJ(μθ)=∇θ∫Sν0(s)Vμθ(s)ds=∫Sν0(s)∇θVμθ(s)ds=∫Sν0(s)(∫S∑t=0∞γtp(s→s′,t,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′)ds=∫S(∫S∑t=0∞γtν0(s)p(s→s′,t,μθ)ds)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′=∫Sνμθ(s)∇θμθ(s)∇aQμθ(s′,a)∣a=μθ(s′)ds=Es∼νμθ[∇θμθ(s)∇aQμθ(s′,a)∣a=μθ(s′)]\begin{aligned} \nabla_\theta J(\mu_\theta) &= \nabla_\theta \int_{\mathcal{S}} \nu_0 (s) V^{\mu_\theta}(s) \mathrm{d}s \\ &= \int_{\mathcal{S}} \nu_0 (s) \nabla_\theta V^{\mu_\theta}(s) \mathrm{d}s \\ &= \int_{\mathcal{S}} \nu_0 (s) \bigg( \int_{\mathcal{S}} \sum_{t=0}^\infin \gamma^t p(s \rightarrow s', t, \mu_\theta) \nabla_\theta \mu_\theta(s') \nabla_a Q^{\mu_\theta}(s',a)|_{a=\mu_\theta(s')}\mathrm{d}s' \bigg) \mathrm{d}s \\ &= \int_{\mathcal{S}} \bigg( \int_{\mathcal{S}} \sum_{t=0}^\infin \gamma^t \nu_0 (s) p(s \rightarrow s', t, \mu_\theta) \mathrm{d}s \bigg) \nabla_\theta \mu_\theta(s') \nabla_a Q^{\mu_\theta}(s',a)|_{a=\mu_\theta(s')}\mathrm{d}s'\\ &= \int_{\mathcal{S}} \nu^{\mu_\theta}(s) \nabla_\theta \mu_\theta(s) \nabla_a Q^{\mu_\theta}(s',a)|_{a=\mu_\theta(s')}\mathrm{d}s\\ &= \mathbb{E}_{s\sim\nu^{\mu_\theta}}[\nabla_\theta \mu_\theta(s) \nabla_a Q^{\mu_\theta}(s',a)|_{a=\mu_\theta(s')}]\\ \end{aligned} ∇θJ(μθ)=∇θ∫Sν0(s)Vμθ(s)ds=∫Sν0(s)∇θVμθ(s)ds=∫Sν0(s)(∫St=0∑∞γtp(s→s′,t,μθ)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′)ds=∫S(∫St=0∑∞γtν0(s)p(s→s′,t,μθ)ds)∇θμθ(s′)∇aQμθ(s′,a)∣a=μθ(s′)ds′=∫Sνμθ(s)∇θμθ(s)∇aQμθ(s′,a)∣a=μθ(s′)ds=Es∼νμθ[∇θμθ(s)∇aQμθ(s′,a)∣a=μθ(s′)]
以上过程证明的是在线策略形式的 DPG 定理,期望下标明确表示s∼νμθs\sim\nu^{\mu_\theta}s∼νμθ。为了得到离线策略形式的 DPG 定理,我们只需要将目标函数写成J(θ)=∫SνβVμθ(s)ds=∫SνβQμθ(s,μθ(s))ds\displaystyle J(\theta)=\int_{\mathcal{S}} \nu^\beta V^{\mu_\theta}(s)\mathrm{d}s=\int_{\mathcal{S}} \nu^\beta Q^{\mu_\theta}(s,\mu_\theta(s))\mathrm{d}sJ(θ)=∫SνβVμθ(s)ds=∫SνβQμθ(s,μθ(s))ds,然后进行求导即可。
13.6 参考文献
[1] SILVER D, LEVER G, HEESS N, et al. Deterministic policy gradient algorithms [C]// International conference on machine learning, PMLR, 2014: 387-395.
[2] LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning [C]// International conference on learning representation, 2016.
14 SAC 算法
14.1 简介
之前的章节提到过在线策略算法的采样效率比较低,我们通常更倾向于使用离线策略算法。然而,虽然 DDPG 是离线策略算法,但是它的训练非常不稳定,收敛性较差,对超参数比较敏感,也难以适应不同的复杂环境。2018 年,一个更加稳定的离线策略算法 Soft Actor-Critic(SAC)被提出。SAC 的前身是 Soft Q-learning,它们都属于最大熵强化学习的范畴。Soft Q-learning 不存在一个显式的策略函数,而是使用一个QQQ函数的波尔兹曼分布,在连续空间下求解非常麻烦。于是 SAC 提出使用一个 Actor 表示策略函数,从而解决这个问题。目前,在无模型的强化学习算法中,SAC 是一个非常高效的算法,它学习一个随机性策略,在不少标准环境中取得了领先的成绩。
14.2 最大熵强化学习
熵(entropy)表示对一个随机变量的随机程度的度量。具体而言,如果XXX是一个随机变量,且它的概率密度函数为ppp,那么它的熵HHH就被定义为
H(X)=Ex∼p[−logp(x)]\mathcal{H}(X) = \mathbb{E}_{x\sim p}[-\log p(x)] H(X)=Ex∼p[−logp(x)]
在强化学习中,我们可以使用H(π(⋅∣s))\mathcal{H}\big(\pi(\cdot|s)\big)H(π(⋅∣s))来表示策略π\piπ在状态sss下的随机程度。
最大熵强化学习(maximum entropy RL)的思想就是除了要最大化累积奖励,还要使得策略更加随机。如此,强化学习的目标中就加入了一项熵的正则项,定义为
πMaxEnt∗=arg maxπE(st,at)∼ρ(π)∑t∞[r(st,at)+αH(π(⋅∣st))]\pi^*_{\text{MaxEnt}} = \argmax_\pi \mathbb{E}_{(s_t, a_t)\sim\rho(\pi)} \sum_t^\infin \bigg[r(s_t, a_t) + \alpha \mathcal{H}\big(\pi(\cdot|s_t)\big)\bigg] πMaxEnt∗=πargmaxE(st,at)∼ρ(π)t∑∞[r(st,at)+αH(π(⋅∣st))]
其中,α\alphaα是一个正则化的系数,用来控制熵的重要程度。
熵正则化增加了强化学习算法的探索程度,α\alphaα越大,探索性就越强,有助于加速后续的策略学习,并减少策略陷入较差的局部最优的可能性。传统强化学习和最大熵强化学习的区别如图 14-1 所示。
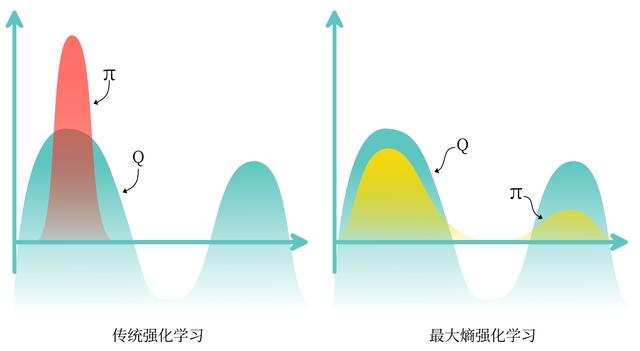
图14-1 传统强化学习和最大熵强化学习的区别
在离散的动作空间中,有:H(π(⋅∣s))=−∑atπ(at∣st)log(π(at∣st))\displaystyle \mathcal{H}\big(\pi(\cdot|s)\big) = -\sum_{a_t} \pi(a_t|s_t)\log\big(\pi(a_t|s_t)\big)H(π(⋅∣s))=−at∑π(at∣st)log(π(at∣st))
在连续的动作空间中,有:H(π(⋅∣s))=−∫atlog(π(at∣st))dat\displaystyle \mathcal{H}\big(\pi(\cdot|s)\big) = -\int_{a_t} \log\big(\pi(a_t|s_t)\big) \mathrm{d}a_tH(π(⋅∣s))=−∫atlog(π(at∣st))dat
注意到,最大熵并不是只关注当前状态sts_tst下的最大熵,而是考虑到从t时间开始的未来的所有熵的和。
基于能量的模型
基于能量的模型(energy-based model,EBM)目标:(其中 ϕ(x)\phi(x)ϕ(x)可以理解为对状态xxx的打分函数)
maxpEx∼p[ϕ(x)]+αH(p)\max_p \mathbb{E}_{x\sim p} [\phi(x)] + \alpha \mathcal{H}(p) pmaxEx∼p[ϕ(x)]+αH(p)
上述目标最终会收敛到的最优分布p∗p^*p∗称为玻尔兹曼分布(Boltzmann distribution),其中
p∗(x)∝eϕ(x)α=e−E(x)p^*(x) \propto e^{\frac{\phi(x)}{\alpha}} = e^{-\mathcal{E}(x)} p∗(x)∝eαϕ(x)=e−E(x)
称α\alphaα为温度系数。如果α\alphaα设置较大,则分布会较为平缓,如果α\alphaα设置较小,分布会陡峭,并且尽量集中在一点附近。
基于上述目标函数求解,对整个式子同除温度系数α\alphaα,然后推导可得:
maxpEx∼p[ϕ(x)]+αH(p)=maxpEx∼p[ϕ(x)]α+H(p)=maxpEx∼p[ϕ(x)α]−Ex∼p[logp(x)]=maxpEx∼p[ϕ(x)α−logp(x)]=−maxpEx∼p[logp(x)−ϕ(x)α]=minpEx∼p[logp(x)−ϕ(x)α]\begin{aligned} \max_p \mathbb{E}_{x\sim p} [\phi(x)] + \alpha \mathcal{H}(p) &= \max_p \dfrac{\mathbb{E}_{x\sim p} [\phi(x)]}{\alpha} + \mathcal{H}(p)\\ &= \max_p \mathbb{E}_{x\sim p} [\dfrac{\phi(x)}{\alpha}] - \mathbb{E}_{x\sim p}[\log p(x)]\\ &= \max_p \mathbb{E}_{x\sim p} \bigg[\dfrac{\phi(x)}{\alpha} - \log p(x)\bigg]\\ &= -\max_p \mathbb{E}_{x\sim p} \bigg[\log p(x) - \dfrac{\phi(x)}{\alpha}\bigg]\\ &= \min_p \mathbb{E}_{x\sim p} \bigg[\log p(x) - \dfrac{\phi(x)}{\alpha}\bigg]\\ \end{aligned} pmaxEx∼p[ϕ(x)]+αH(p)=pmaxαEx∼p[ϕ(x)]+H(p)=pmaxEx∼p[αϕ(x)]−Ex∼p[logp(x)]=pmaxEx∼p[αϕ(x)−logp(x)]=−pmaxEx∼p[logp(x)−αϕ(x)]=pminEx∼p[logp(x)−αϕ(x)]
其中,我们设定一个能量函数 E(x)=−ϕ(x)α\mathcal{E}(x) = -\dfrac{\phi(x)}{\alpha}E(x)=−αϕ(x),于是有ϕ(x)α=−E(x)=loge−E(x)\dfrac{\phi(x)}{\alpha} = -\mathcal{E}(x) = \log e^{-\mathcal{E}(x)}αϕ(x)=−E(x)=loge−E(x)
于是继续推导,有:
maxpEx∼p[ϕ(x)]+αH(p)=minpEx∼p[logp(x)−ϕ(x)α]=minpEx∼p[logp(x)−loge−E(x)]=minpKL(p∣∣pϕ)\begin{aligned} \max_p \mathbb{E}_{x\sim p} [\phi(x)] + \alpha \mathcal{H}(p) &= \min_p \mathbb{E}_{x\sim p} \bigg[\log p(x) - \dfrac{\phi(x)}{\alpha}\bigg]\\ &= \min_p \mathbb{E}_{x\sim p} \bigg[\log p(x) - \log e^{-\mathcal{E}(x)}\bigg]\\ &= \min_p KL(p||p_{\phi}) \end{aligned} pmaxEx∼p[ϕ(x)]+αH(p)=pminEx∼p[logp(x)−αϕ(x)]=pminEx∼p[logp(x)−loge−E(x)]=pminKL(p∣∣pϕ)
其中 pϕ(x)=e−E(x)Zp_{\phi}(x) = \dfrac{e^{-\mathcal{E}(x)}}{Z}pϕ(x)=Ze−E(x),ZZZ是归一化系数。于是我们最大化目标函数的任务,就变成最小化两个分布之间的KL Divergence。
基于能量模型的策略优化
在某个状态sss,策略优化目标为:
maxaEa∼π(⋅∣s)[Q(s,a)]+αH[π(⋅∣s)]\max_a \mathbb{E}_{a\sim\pi(\cdot|s)} [Q(s,a)] + \alpha \mathcal{H}[\pi(\cdot|s)] amaxEa∼π(⋅∣s)[Q(s,a)]+αH[π(⋅∣s)]
不难发现,如果这里没有熵的正则化项,则选择使得目标函数最大的动作aaa,就是选择maxaQ(s,a)\max_a Q(s,a)maxaQ(s,a),即 Q-learning。因此这个模型也被称作软Q-Learning,即Soft Q Learning。具体来说,对于两个选项得分分别为0.98和0.99时,QL会选择0.99摈弃0.98,而SQL会保留0.98的选项,以维护最大熵。
最终目标会收敛到最优分布p∗p^*p∗的玻尔兹曼分布(Boltzmann distribution),推导同上:
maxaEa∼π(⋅∣s)[Q(s,a)]+αH[π(⋅∣s)]=maxpEa∼π(⋅∣s)[Q(s,a)]α+H(π(⋅∣s))=maxpEa∼π(⋅∣s)[1αQ(s,a)]−Ea∼π(⋅∣s)[logπ(a∣s)]=maxpEa∼π(⋅∣s)[1αQ(s,a)−logπ(a∣s)]=−maxpEa∼π(⋅∣s)[logπ(a∣s)−1αQ(s,a)]=minpEa∼π(⋅∣s)[logπ(a∣s)−1αQ(s,a)]=minpEa∼π(⋅∣s)[logπ(a∣s)−logexp[1αQ(s,a)]]=minpKL(π∣∣pQ)\begin{aligned} \max_a \mathbb{E}_{a\sim\pi(\cdot|s)} [Q(s,a)] + \alpha \mathcal{H}[\pi(\cdot|s)] &= \max_p \dfrac{\mathbb{E}_{a\sim\pi(\cdot|s)} [Q(s,a)]}{\alpha} + \mathcal{H}(\pi(\cdot|s))\\ &= \max_p \mathbb{E}_{a\sim\pi(\cdot|s)} [\dfrac{1}{\alpha}Q(s,a)] - \mathbb{E}_{a\sim\pi(\cdot|s)}[\log \pi(a|s)]\\ &= \max_p \mathbb{E}_{a\sim\pi(\cdot|s)} \bigg[\dfrac{1}{\alpha}Q(s,a) - \log \pi(a|s)\bigg]\\ &= -\max_p \mathbb{E}_{a\sim\pi(\cdot|s)} \bigg[\log \pi(a|s) - \dfrac{1}{\alpha}Q(s,a)\bigg]\\ &= \min_p \mathbb{E}_{a\sim\pi(\cdot|s)} \bigg[\log \pi(a|s) - \dfrac{1}{\alpha}Q(s,a)\bigg]\\ &= \min_p \mathbb{E}_{a\sim\pi(\cdot|s)} \bigg[\log \pi(a|s) - \log \operatorname{exp}[\dfrac{1}{\alpha}Q(s,a)]\bigg]\\ &= \min_p KL(\pi || p_Q)\\ \end{aligned} amaxEa∼π(⋅∣s)[Q(s,a)]+αH[π(⋅∣s)]=pmaxαEa∼π(⋅∣s)[Q(s,a)]+H(π(⋅∣s))=pmaxEa∼π(⋅∣s)[α1Q(s,a)]−Ea∼π(⋅∣s)[logπ(a∣s)]=pmaxEa∼π(⋅∣s)[α1Q(s,a)−logπ(a∣s)]=−pmaxEa∼π(⋅∣s)[logπ(a∣s)−α1Q(s,a)]=pminEa∼π(⋅∣s)[logπ(a∣s)−α1Q(s,a)]=pminEa∼π(⋅∣s)[logπ(a∣s)−logexp[α1Q(s,a)]]=pminKL(π∣∣pQ)
其中 pQ(s,a)=exp[1αQ(s,a)]Zp_Q(s,a) = \dfrac{\operatorname{exp}[\dfrac{1}{\alpha}Q(s,a)]}{Z}pQ(s,a)=Zexp[α1Q(s,a)],ZZZ是归一化系数,最终的最优策略 πMaxEnt∗(a∣s)∝exp[1αQ(s,a)]\pi^{*}_{\text{MaxEnt}}(a|s)\propto\operatorname{exp}[\dfrac{1}{\alpha}Q(s,a)]πMaxEnt∗(a∣s)∝exp[α1Q(s,a)]
软价值函数 Soft Value Function
在最大熵强化学习框架中,由于目标函数发生了变化,其他的一些定义也有相应的变化。首先是状态价值函数:
V(st)=Eτ∼π[∑l=0∞γl(rt+l)]Vsoft(st)=Eτ∼π[∑l=0∞γl(rt+l+αH(πMaxEnt∗(⋅∣st+l)))]\begin{aligned} V(s_t) &= \mathbb{E}_{\tau\sim\pi} \bigg[ \sum_{l=0}^\infin \gamma^l (r_{t+l}) \bigg]\\ V_{\text{soft}}(s_t) &= \mathbb{E}_{\tau\sim\pi} \bigg[ \sum_{l=0}^\infin \gamma^l \bigg( r_{t+l} + \alpha \mathcal{H}\big( \pi^{*}_{\text{MaxEnt}}(\cdot | s_{t+l}) \big) \bigg) \bigg] \end{aligned} V(st)Vsoft(st)=Eτ∼π[l=0∑∞γl(rt+l)]=Eτ∼π[l=0∑∞γl(rt+l+αH(πMaxEnt∗(⋅∣st+l)))]
然后是动作价值函数:
Q(st,at)=Eτ∼π[∑l=0∞γl(rt+l)]Qsoft(st,at)=Eτ∼π[∑l=0∞γl(rt+l)+α(∑l=1∞γlH(πMaxEnt∗(⋅∣st+l)))]=Eτ∼π[∑l=0∞γl(rt+l+αH(πMaxEnt∗(⋅∣st+l+1)))]=Eτ∼π[∑l=0∞γl(rt+l+αH(πMaxEnt∗(⋅∣st+l)))−αH(πMaxEnt∗(⋅∣st))]=Eτ∼π[rt+∑l=1∞γl(rt+l+αH(πMaxEnt∗(⋅∣st+l)))]\begin{aligned} Q(s_t,a_t) &= \mathbb{E}_{\tau\sim\pi} \bigg[ \sum_{l=0}^\infin \gamma^l (r_{t+l}) \bigg]\\ Q_{\text{soft}}(s_t,a_t) &= \mathbb{E}_{\tau\sim\pi} \bigg[ \sum_{l=0}^\infin \gamma^l(r_{t+l}) + \alpha \bigg( \sum_{l=1}^\infin \gamma^l \mathcal{H}\big( \pi^{*}_{\text{MaxEnt}}(\cdot | s_{t+l}) \big) \bigg) \bigg]\\ &= \mathbb{E}_{\tau\sim\pi} \bigg[ \sum_{l=0}^\infin \gamma^l \bigg( r_{t+l} + \alpha \mathcal{H}\big( \pi^{*}_{\text{MaxEnt}}(\cdot | s_{t+l+1})\big) \bigg) \bigg]\\ &= \mathbb{E}_{\tau\sim\pi} \bigg[ \sum_{l=0}^\infin \gamma^l \bigg( r_{t+l} + \alpha \mathcal{H}\big( \pi^{*}_{\text{MaxEnt}}(\cdot | s_{t+l})\big) \bigg) - \alpha \mathcal{H}\big( \pi^{*}_{\text{MaxEnt}}(\cdot | s_{t})\big) \bigg]\\ &= \mathbb{E}_{\tau\sim\pi} \bigg[ r_t + \sum_{l=1}^\infin \gamma^l \bigg( r_{t+l} + \alpha \mathcal{H}\big( \pi^{*}_{\text{MaxEnt}}(\cdot | s_{t+l})\big) \bigg) \bigg]\\ \end{aligned} Q(st,at)Qsoft(st,at)=Eτ∼π[l=0∑∞γl(rt+l)]=Eτ∼π[l=0∑∞γl(rt+l)+α(l=1∑∞γlH(πMaxEnt∗(⋅∣st+l)))]=Eτ∼π[l=0∑∞γl(rt+l+αH(πMaxEnt∗(⋅∣st+l+1)))]=Eτ∼π[l=0∑∞γl(rt+l+αH(πMaxEnt∗(⋅∣st+l)))−αH(πMaxEnt∗(⋅∣st))]=Eτ∼π[rt+l=1∑∞γl(rt+l+αH(πMaxEnt∗(⋅∣st+l)))]
根据以上定义,两者的关系(贝尔曼soft方程)为:
Vsoft(st)=Eat∼π(⋅∣st)[Qsoft(st,at)]+αH(π(⋅∣st))Qsoft(st,at)=Es′∼p[rt+γVsoft(s′)]=Es′∼p,a′∼π(⋅∣s′)[rt+γ(Qsoft(s′,a′)+αH(π(⋅∣s′)))]\begin{aligned} V_{\text{soft}}(s_t) &= \mathbb{E}_{a_t \sim \pi(\cdot|s_t)} \Big[ Q_{\text{soft}}(s_t,a_t) \Big] + \alpha \mathcal{H}\big( \pi(\cdot | s_{t})\big)\\ Q_{\text{soft}}(s_t,a_t) &= \mathbb{E}_{s' \sim p} \Big[r_t + \gamma V_{\text{soft}}(s') \Big]\\ &= \mathbb{E}_{s' \sim p, a'\sim\pi(\cdot|s')} \Big[r_t + \gamma \Big(Q_{\text{soft}}(s',a') + \alpha \mathcal{H}(\pi(\cdot|s'))\Big) \Big] \end{aligned} Vsoft(st)Qsoft(st,at)=Eat∼π(⋅∣st)[Qsoft(st,at)]+αH(π(⋅∣st))=Es′∼p[rt+γVsoft(s′)]=Es′∼p,a′∼π(⋅∣s′)[rt+γ(Qsoft(s′,a′)+αH(π(⋅∣s′)))]
14.3 Soft 策略迭代
Soft 策略优化的目标:
maxπEa∼π(⋅∣s)[Qsoft(s,a)]+αH(π(⋅∣s))\max_\pi \mathbb{E}_{a\sim\pi(\cdot|s)} \Big[ Q_{\text{soft}}(s,a) \Big] + \alpha \mathcal{H}\big(\pi(\cdot|s)\big) πmaxEa∼π(⋅∣s)[Qsoft(s,a)]+αH(π(⋅∣s))
基于能量模型:
πMaxEnt∗(a∣s)∝exp(1αQsoft(s,a))\pi^{*}_{\text{MaxEnt}}(a|s) \propto \operatorname{exp}\big( \dfrac{1}{\alpha} Q_{\text{soft}}(s,a) \big) πMaxEnt∗(a∣s)∝exp(α1Qsoft(s,a))
价值迭代部分的状态值函数更新:
其中利用到了LogSumExp\operatorname{LogSumExp}LogSumExp操作,是一种平滑化的 argmax\operatorname{argmax}argmax 操作,它计算了一个加权平均值。(在连续的概率图中,可以用来找概率密度较大的第一个点)
LogSumExp(x)=离散log∑i=1nexip(x)LogSumExp(x)=连续log∫exdx\begin{aligned} \operatorname{LogSumExp} (x) &\overset{\text{离散}}{=} \log \sum_{i=1}^n e^{x_i} p(x)\\ \operatorname{LogSumExp} (x) &\overset{\text{连续}}{=} \log \int e^x dx \end{aligned} LogSumExp(x)LogSumExp(x)=离散logi=1∑nexip(x)=连续log∫exdx
收敛性保证(论文中有证明):当Q,VQ,VQ,V按照如下更新方式收敛至Qsoft∗,Vsoft∗Q^*_{\text{soft}},V^*_{\text{soft}}Qsoft∗,Vsoft∗时,π\piπ收敛至πMxEnt∗\pi^*_{\text{MxEnt}}πMxEnt∗
Qsoft(st,at)←rt+γEst+1∼p[Vsoft(st+1)],∀st,atVsoft(st)←αlog∫exp[1αQsoft(st,a′)]da′,∀st\begin{aligned} Q_{\text{soft}}(s_t,a_t) &\leftarrow r_t + \gamma \mathbb{E}_{s_{t+1}\sim p}[V_{\text{soft}}(s_{t+1})], \forall s_t, a_t\\ V_{\text{soft}}(s_t) &\leftarrow \alpha \log \int \operatorname{exp} \bigg[\dfrac{1}{\alpha} Q_{\text{soft}}(s_t,a')\bigg]\mathrm{d}a', \forall s_t \end{aligned} Qsoft(st,at)Vsoft(st)←rt+γEst+1∼p[Vsoft(st+1)],∀st,at←αlog∫exp[α1Qsoft(st,a′)]da′,∀st
当状态价值函数和动作价值函数在当前策略下收敛到最优后(完成策略评估),对应的最优策略为
πMaxEnt∗(a∣s)=exp(1α(Qsoft∗(st,at)−Vsoft∗(st)))\pi^{*}_{\text{MaxEnt}}(a|s) = \operatorname{exp}\bigg( \dfrac{1}{\alpha} \Big(Q^*_{\text{soft}}(s_t,a_t) - V^*_{\text{soft}}(s_t) \Big)\bigg) πMaxEnt∗(a∣s)=exp(α1(Qsoft∗(st,at)−Vsoft∗(st)))
根据该 Soft 贝尔曼方程,在有限的状态和动作空间情况下,Soft 策略评估可以收敛到策略π\piπ的 Soft QQQ函数。然后,根据如下 Soft 策略提升公式可以改进策略:
πnew=arg minπ′DKL(π′(⋅∣s),exp[1αQπold(s,⋅)]Zπold(s,⋅))=arg minπ′DKL(π′(⋅∣s),πMaxEnt∗(a∣s))\begin{aligned} \pi_{\text{new}} &= \argmin_{\pi'} D_{KL}\bigg( \pi'(\cdot|s), \dfrac{\operatorname{exp}[{\dfrac{1}{\alpha} Q^{\pi_{\text{old}}}(s, \cdot)}]}{Z^{\pi_{\text{old}}}(s, \cdot)} \bigg)\\ &= \argmin_{\pi'} D_{KL} \bigg( \pi'(\cdot|s), \pi^{*}_{\text{MaxEnt}}(a|s) \bigg) \end{aligned} πnew=π′argminDKL(π′(⋅∣s),Zπold(s,⋅)exp[α1Qπold(s,⋅)])=π′argminDKL(π′(⋅∣s),πMaxEnt∗(a∣s))
重复交替使用 Soft 策略评估和 Soft 策略提升,最终策略可以收敛到最大熵强化学习目标中的最优策略。但该 Soft 策略迭代方法只适用于表格型(tabular)设置的情况,即状态空间和动作空间是有限的情况。在连续空间下,我们需要通过参数化函数QQQ和策略π\piπ来近似这样的迭代。
14.4 SAC
在 SAC 算法中,我们为两个动作价值函数QQQ(参数分别为ω1\omega_1ω1和ω2\omega_2ω2)和一个策略函数π\piπ(参数为θ\thetaθ)建模。基于 Double DQN 的思想,SAC 使用两个QQQ网络,但每次用QQQ网络时会挑选一个QQQ值小的网络,从而缓解QQQ值过高估计的问题。任意一个函数QQQ的损失函数为:
LQ(ω)=E(st,at,rt,st+1)∼R[12(Qω(st,at)−(rt+γVω−(st+1)))2]=E(st,at,rt,st+1)∼R,at+1∼πθ(⋅∣st+1)[12(Qω(st,at)−(rt+γ(minj=1,2Qωj−(st+1,at+1)−αlogπ(at+1∣st+1))))2]\begin{aligned} L_Q(\omega) &= \mathbb{E}_{(s_t,a_t,r_t,s_{t+1}) \sim R} \bigg[ \dfrac{1}{2} \Big( Q_\omega(s_t,a_t) - (r_t + \gamma V_{\omega^{-}}(s_{t+1})) \Big)^2 \bigg]\\ &= \mathbb{E}_{(s_t,a_t,r_t,s_{t+1}) \sim R, a_{t+1}\sim\pi_{\theta}(\cdot|s_{t+1})} \bigg[ \dfrac{1}{2} \Big( Q_\omega(s_t,a_t) - \Big(r_t + \gamma \big( \min_{j=1,2} Q_{\omega^{-}_j}(s_{t+1}, a_{t+1}) - \alpha \log \pi (a_{t+1}|s_{t+1}) \big)\Big) \Big)^2 \bigg]\\ \end{aligned} LQ(ω)=E(st,at,rt,st+1)∼R[21(Qω(st,at)−(rt+γVω−(st+1)))2]=E(st,at,rt,st+1)∼R,at+1∼πθ(⋅∣st+1)[21(Qω(st,at)−(rt+γ(j=1,2minQωj−(st+1,at+1)−αlogπ(at+1∣st+1))))2]
其中,RRR是策略过去收集的数据,因为 SAC 是一种离线策略算法。为了让训练更加稳定,这里使用了目标QQQ网络Qω−Q_{\omega^{-}}Qω−,同样是两个目标QQQ网络,与两个QQQ网络一一对应。SAC 中目标QQQ网络的更新方式与 DDPG 中的更新方式一样。
策略π\piπ的损失函数由 KL 散度得到,化简后为:
Lπ(θ)=Est∼R,at∼πθ[αlog(πθ(at∣st))−Qω(st,at)]L_{\pi}(\theta) = \mathbb{E}_{s_t\sim R, a_t\sim \pi_\theta} \bigg[ \alpha\log\Big(\pi_\theta(a_t|s_t)\Big) - Q_\omega(s_t,a_t) \bigg] Lπ(θ)=Est∼R,at∼πθ[αlog(πθ(at∣st))−Qω(st,at)]
可以理解为最大化函数VVV,因为有V(st)=Eat∼π[Q(st,at)−αlogπ(at∣st)]V(s_t) = \mathbb{E}_{a_t \sim \pi}[Q(s_t, a_t) - \alpha \log \pi(a_t|s_t)]V(st)=Eat∼π[Q(st,at)−αlogπ(at∣st)]。
对连续动作空间的环境,SAC 算法的策略输出高斯分布的均值和标准差,但是根据高斯分布来采样动作的过程是不可导的。因此,我们需要用到重参数化技巧(reparameterization trick)。重参数化的做法是先从一个单位高斯分布N\mathcal{N}N采样,再把采样值乘以标准差后加上均值。这样就可以认为是从策略高斯分布采样,并且这样对于策略函数是可导的。我们将其表示为at=fθ(ϵt;st)a_t = f_\theta(\epsilon_t;s_t)at=fθ(ϵt;st),其中ϵt\epsilon_tϵt是一个噪声随机变量。同时考虑到两个函数QQQ,重写策略的损失函数:
Lπ(θ)=Est∼R,ϵt∼N[αlog(πθ(fθ(ϵt;st)))−minj=1,2Qωj[st,fθ(ϵt;st)]]L_\pi(\theta) = \mathbb{E}_{s_t \sim R, \epsilon_t \sim \mathcal{N}} \bigg[ \alpha \log \Big(\pi_\theta\big(f_\theta(\epsilon_t;s_t)\big)\Big) - \min_{j=1,2} Q_{\omega_j} [s_t, f_\theta(\epsilon_t;s_t)] \bigg] Lπ(θ)=Est∼R,ϵt∼N[αlog(πθ(fθ(ϵt;st)))−j=1,2minQωj[st,fθ(ϵt;st)]]
自动调整熵正则项
在 SAC 算法中,如何选择熵正则项的系数非常重要。在不同的状态下需要不同大小的熵:在最优动作不确定的某个状态下,熵的取值应该大一点;而在某个最优动作比较确定的状态下,熵的取值可以小一点。为了自动调整熵正则项,SAC 将强化学习的目标改写为一个带约束的优化问题:
maxπEπ[∑tr(st,at)]s.t. E(st,at)∼ρπ[−log(πt(at∣st))]≥H0\begin{aligned} & \max_\pi \mathbb{E}_{\pi} \bigg[ \sum_t r(s_t, a_t) \bigg]\\ & \text{s.t. } \mathbb{E}_{(s_t,a_t)\sim\rho_\pi} [-\log(\pi_t (a_t|s_t))] \ge \mathcal{H}_0 \end{aligned} πmaxEπ[t∑r(st,at)]s.t. E(st,at)∼ρπ[−log(πt(at∣st))]≥H0
也就是最大化期望回报,同时约束熵的均值大于H0\mathcal{H}_0H0。通过一些数学技巧化简后,得到α\alphaα的损失函数:
L(α)=Est∼R,at∼π(⋅∣st)[−αlogπ(at∣st)−αH0]L(\alpha) = \mathbb{E}_{s_t\sim R, a_t \sim \pi(\cdot|s_t)} [-\alpha\log\pi (a_t|s_t) - \alpha \mathcal{H}_0] L(α)=Est∼R,at∼π(⋅∣st)[−αlogπ(at∣st)−αH0]
即当策略的熵低于目标值H0\mathcal{H}_0H0时,训练目标L(α)L(\alpha)L(α)会使α\alphaα的值增大,进而在上述最小化损失函数Lπ(β)L_\pi(\beta)Lπ(β)的过程中增加了策略熵对应项的重要性;而当策略的熵高于目标值H0\mathcal{H}_0H0时,训练目标L(α)L(\alpha)L(α)会使α\alphaα的值减小,进而使得策略训练时更专注于价值提升。
至此,我们介绍完了 SAC 算法的整体思想,它的具体算法流程如下:
- 用随机的网络参数ω1\omega_1ω1,ω2\omega_2ω2和θ\thetaθ分别初始化 Critic 网络Qω1(s,a)Q_{\omega_1}(s,a)Qω1(s,a), Qω2(s,a)Q_{\omega_2}(s,a)Qω2(s,a)和 Actor 网络 πθ(s)\pi_\theta(s)πθ(s)
- 复制相同的参数ω1−←ω1\omega_1^{-}\leftarrow \omega_1ω1−←ω1,ω2−←ω2\omega_2^{-} \leftarrow \omega_2ω2−←ω2,分别初始化目标网络和Qω1−Q_{\omega_1^{-}}Qω1−和Qω2−Q_{\omega_2^{-}}Qω2−
- 初始化经验回放池RRR
- for 序列e=1→Ee=1\rightarrow Ee=1→E do
- 获取环境初始状态s1s_1s1
- for 时间步t=1→Tt=1\rightarrow Tt=1→T do
- 根据当前策略选择动作at=πθ(st)a_t=\pi_\theta(s_t)at=πθ(st)
- 执行动作ata_tat,获得奖励rtr_trt,环境状态变为st+1s_{t+1}st+1
- 将(st,at,rt,st+1)(s_t,a_t,r_t,s_{t+1})(st,at,rt,st+1)存入回放池RRR
- for 训练轮数k=1→Kk=1\rightarrow Kk=1→K do
- 从RRR中采样NNN个元组{(si,ai,ri,si+1)}i=1,⋯ ,N\{(s_i,a_i,r_i,s_{i+1})\}_{i=1,\cdots,N}{(si,ai,ri,si+1)}i=1,⋯,N
- 对每个元组,用目标网络计算yi=ri+γminj=1,2Qωj−(si+1,ai+1)−αlogπθ(ai+1∣si+1)\displaystyle y_i=r_i+\gamma\min_{j=1,2}Q_{\omega_j^{-}}(s_{i+1},a_{i+1})-\alpha\log\pi_\theta(a_{i+1}|s_{i+1})yi=ri+γj=1,2minQωj−(si+1,ai+1)−αlogπθ(ai+1∣si+1),其中ai+1∼πθ(⋅∣si+1)a_{i+1} \sim \pi_\theta(\cdot|s_{i+1})ai+1∼πθ(⋅∣si+1)
- 对两个 Critic 网络都进行如下更新:对j=1,2j=1,2j=1,2,最小化损失函数L=1N∑i=1N(yi−Qωj(si,ai))2\displaystyle L=\dfrac{1}{N} \sum_{i=1}^N (y_i - Q_{\omega_j}(s_i,a_i))^2L=N1i=1∑N(yi−Qωj(si,ai))2
- 用重参数化技巧采样动作a~\tilde{a}a~,然后用以下损失函数更新当前 Actor 网络:
Lπ(θ)=1N∑i=1N(αlogπθ(a~i∣si)−minj=1,2Qωj(si,a~i))L_\pi(\theta) = \dfrac{1}{N} \sum_{i=1}^N \bigg( \alpha\log\pi_\theta(\tilde{a}_i|s_i) - \min_{j=1,2} Q_{\omega_j}(s_i,\tilde{a}_i) \bigg) Lπ(θ)=N1i=1∑N(αlogπθ(a~i∣si)−j=1,2minQωj(si,a~i))
- 更新熵正则项的系数α\alphaα
- 更新目标网络:
ω1−←τω1+(1−τ)ω1−ω2−←τω2+(1−τ)ω2−\begin{aligned} \omega_1^{-} &\leftarrow \tau\omega_1 + (1-\tau)\omega_1^{-}\\ \omega_2^{-} &\leftarrow \tau\omega_2 + (1-\tau)\omega_2^{-}\\ \end{aligned} ω1−ω2−←τω1+(1−τ)ω1−←τω2+(1−τ)ω2−
- end for
- end for
- end for
14.5 SAC 代码实践
我们来看一下 SAC 的代码实现,首先在倒立摆环境下进行实验,然后再尝试将 SAC 应用到与离散动作交互的车杆环境。
首先我们导入需要用到的库。
import random
import gym
import numpy as np
from tqdm import tqdm
import torch
import torch.nn.functional as F
from torch.distributions import Normal
import matplotlib.pyplot as plt
import rl_utils
接下来定义策略网络和价值网络。由于处理的是与连续动作交互的环境,策略网络输出一个高斯分布的均值和标准差来表示动作分布;而价值网络的输入是状态和动作的拼接向量,输出一个实数来表示动作价值。
class PolicyNetContinuous(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
super(PolicyNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc_mu = torch.nn.Linear(hidden_dim, action_dim)
self.fc_std = torch.nn.Linear(hidden_dim, action_dim)
self.action_bound = action_bound
def forward(self, x):
x = F.relu(self.fc1(x))
mu = self.fc_mu(x)
std = F.softplus(self.fc_std(x))
dist = Normal(mu, std)
normal_sample = dist.rsample() # rsample()是重参数化采样
log_prob = dist.log_prob(normal_sample)
action = torch.tanh(normal_sample)
# 计算tanh_normal分布的对数概率密度
log_prob = log_prob - torch.log(1 - torch.tanh(action).pow(2) + 1e-7)
action = action * self.action_bound
return action, log_prob
class QValueNetContinuous(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(QValueNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
self.fc_out = torch.nn.Linear(hidden_dim, 1)
def forward(self, x, a):
cat = torch.cat([x, a], dim=1)
x = F.relu(self.fc1(cat))
x = F.relu(self.fc2(x))
return self.fc_out(x)
然后我们来看一下 SAC 算法的主要代码。如 14.4 节所述,SAC 使用两个 Critic 网络Qω1Q_{\omega_1}Qω1和Qω2Q_{\omega_2}Qω2来使 Actor 的训练更稳定,而这两个 Critic 网络在训练时则各自需要一个目标价值网络。因此,SAC 算法一共用到 5 个网络,分别是一个策略网络、两个价值网络和两个目标价值网络。
class SACContinuous:
''' 处理连续动作的SAC算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, action_bound,
actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma,
device):
self.actor = PolicyNetContinuous(state_dim, hidden_dim, action_dim,
action_bound).to(device) # 策略网络
self.critic_1 = QValueNetContinuous(state_dim, hidden_dim,
action_dim).to(device) # 第一个Q网络
self.critic_2 = QValueNetContinuous(state_dim, hidden_dim,
action_dim).to(device) # 第二个Q网络
self.target_critic_1 = QValueNetContinuous(state_dim,
hidden_dim, action_dim).to(
device) # 第一个目标Q网络
self.target_critic_2 = QValueNetContinuous(state_dim,
hidden_dim, action_dim).to(
device) # 第二个目标Q网络
# 令目标Q网络的初始参数和Q网络一样
self.target_critic_1.load_state_dict(self.critic_1.state_dict())
self.target_critic_2.load_state_dict(self.critic_2.state_dict())
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
lr=actor_lr)
self.critic_1_optimizer = torch.optim.Adam(self.critic_1.parameters(),
lr=critic_lr)
self.critic_2_optimizer = torch.optim.Adam(self.critic_2.parameters(),
lr=critic_lr)
# 使用alpha的log值,可以使训练结果比较稳定
self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float)
self.log_alpha.requires_grad = True # 可以对alpha求梯度
self.log_alpha_optimizer = torch.optim.Adam([self.log_alpha],
lr=alpha_lr)
self.target_entropy = target_entropy # 目标熵的大小
self.gamma = gamma
self.tau = tau
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.actor(state)[0]
return [action.item()]
def calc_target(self, rewards, next_states, dones): # 计算目标Q值
next_actions, log_prob = self.actor(next_states)
entropy = -log_prob
q1_value = self.target_critic_1(next_states, next_actions)
q2_value = self.target_critic_2(next_states, next_actions)
next_value = torch.min(q1_value,
q2_value) + self.log_alpha.exp() * entropy
td_target = rewards + self.gamma * next_value * (1 - dones)
return td_target
def soft_update(self, net, target_net):
for param_target, param in zip(target_net.parameters(),
net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - self.tau) +
param.data * self.tau)
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'],
dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
# 和之前章节一样,对倒立摆环境的奖励进行重塑以便训练
rewards = (rewards + 8.0) / 8.0
# 更新两个Q网络
td_target = self.calc_target(rewards, next_states, dones)
critic_1_loss = torch.mean(
F.mse_loss(self.critic_1(states, actions), td_target.detach()))
critic_2_loss = torch.mean(
F.mse_loss(self.critic_2(states, actions), td_target.detach()))
self.critic_1_optimizer.zero_grad()
critic_1_loss.backward()
self.critic_1_optimizer.step()
self.critic_2_optimizer.zero_grad()
critic_2_loss.backward()
self.critic_2_optimizer.step()
# 更新策略网络
new_actions, log_prob = self.actor(states)
entropy = -log_prob
q1_value = self.critic_1(states, new_actions)
q2_value = self.critic_2(states, new_actions)
actor_loss = torch.mean(-self.log_alpha.exp() * entropy -
torch.min(q1_value, q2_value))
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# 更新alpha值
alpha_loss = torch.mean(
(entropy - self.target_entropy).detach() * self.log_alpha.exp())
self.log_alpha_optimizer.zero_grad()
alpha_loss.backward()
self.log_alpha_optimizer.step()
self.soft_update(self.critic_1, self.target_critic_1)
self.soft_update(self.critic_2, self.target_critic_2)
接下来我们就在倒立摆环境上尝试一下 SAC 算法吧!
env_name = 'Pendulum-v0'
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
action_bound = env.action_space.high[0] # 动作最大值
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
actor_lr = 3e-4
critic_lr = 3e-3
alpha_lr = 3e-4
num_episodes = 100
hidden_dim = 128
gamma = 0.99
tau = 0.005 # 软更新参数
buffer_size = 100000
minimal_size = 1000
batch_size = 64
target_entropy = -env.action_space.shape[0]
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = SACContinuous(state_dim, hidden_dim, action_dim, action_bound,
actor_lr, critic_lr, alpha_lr, target_entropy, tau,
gamma, device)
return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes,
replay_buffer, minimal_size,
batch_size)
Iteration 0: 100%|██████████| 10/10 [00:09<00:00, 1.03it/s, episode=10, return=-1534.655]
Iteration 1: 100%|██████████| 10/10 [00:18<00:00, 1.83s/it, episode=20, return=-1085.715]
Iteration 2: 100%|██████████| 10/10 [00:15<00:00, 1.60s/it, episode=30, return=-364.507]
Iteration 3: 100%|██████████| 10/10 [00:13<00:00, 1.37s/it, episode=40, return=-222.485]
Iteration 4: 100%|██████████| 10/10 [00:13<00:00, 1.36s/it, episode=50, return=-157.978]
Iteration 5: 100%|██████████| 10/10 [00:13<00:00, 1.37s/it, episode=60, return=-166.056]
Iteration 6: 100%|██████████| 10/10 [00:13<00:00, 1.38s/it, episode=70, return=-143.147]
Iteration 7: 100%|██████████| 10/10 [00:13<00:00, 1.37s/it, episode=80, return=-127.939]
Iteration 8: 100%|██████████| 10/10 [00:14<00:00, 1.42s/it, episode=90, return=-180.905]
Iteration 9: 100%|██████████| 10/10 [00:14<00:00, 1.41s/it, episode=100, return=-171.265]
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()
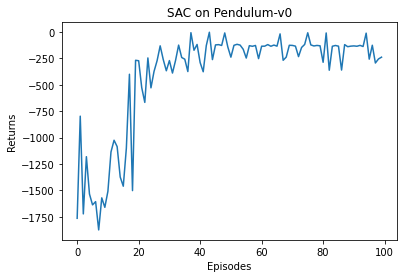
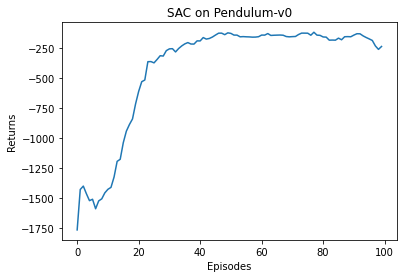
可以发现,SAC 在倒立摆环境中的表现非常出色。SAC 算法原本是针对连续动作交互的环境提出的,那一个比较自然的问题便是:SAC 能否处理与离散动作交互的环境呢?答案是肯定的,但是我们要做一些相应的修改。首先,策略网络和价值网络的网络结构将发生如下改变:
- 策略网络的输出修改为在离散动作空间上的 softmax 分布;
- 价值网络直接接收状态和离散动作空间的分布作为输入。
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
class QValueNet(torch.nn.Module):
''' 只有一层隐藏层的Q网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(QValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
该策略网络输出一个离散的动作分布,所以在价值网络的学习过程中,不需要再对下一个动作at+1a_{t+1}at+1进行采样,而是直接通过概率计算来得到下一个状态的价值。同理,在α\alphaα的损失函数计算中,也不需要再对动作进行采样。
class SAC:
''' 处理离散动作的SAC算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
alpha_lr, target_entropy, tau, gamma, device):
# 策略网络
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
# 第一个Q网络
self.critic_1 = QValueNet(state_dim, hidden_dim, action_dim).to(device)
# 第二个Q网络
self.critic_2 = QValueNet(state_dim, hidden_dim, action_dim).to(device)
self.target_critic_1 = QValueNet(state_dim, hidden_dim,
action_dim).to(device) # 第一个目标Q网络
self.target_critic_2 = QValueNet(state_dim, hidden_dim,
action_dim).to(device) # 第二个目标Q网络
# 令目标Q网络的初始参数和Q网络一样
self.target_critic_1.load_state_dict(self.critic_1.state_dict())
self.target_critic_2.load_state_dict(self.critic_2.state_dict())
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
lr=actor_lr)
self.critic_1_optimizer = torch.optim.Adam(self.critic_1.parameters(),
lr=critic_lr)
self.critic_2_optimizer = torch.optim.Adam(self.critic_2.parameters(),
lr=critic_lr)
# 使用alpha的log值,可以使训练结果比较稳定
self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float)
self.log_alpha.requires_grad = True # 可以对alpha求梯度
self.log_alpha_optimizer = torch.optim.Adam([self.log_alpha],
lr=alpha_lr)
self.target_entropy = target_entropy # 目标熵的大小
self.gamma = gamma
self.tau = tau
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
# 计算目标Q值,直接用策略网络的输出概率进行期望计算
def calc_target(self, rewards, next_states, dones):
next_probs = self.actor(next_states)
next_log_probs = torch.log(next_probs + 1e-8)
entropy = -torch.sum(next_probs * next_log_probs, dim=1, keepdim=True)
q1_value = self.target_critic_1(next_states)
q2_value = self.target_critic_2(next_states)
min_qvalue = torch.sum(next_probs * torch.min(q1_value, q2_value),
dim=1,
keepdim=True)
next_value = min_qvalue + self.log_alpha.exp() * entropy
td_target = rewards + self.gamma * next_value * (1 - dones)
return td_target
def soft_update(self, net, target_net):
for param_target, param in zip(target_net.parameters(),
net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - self.tau) +
param.data * self.tau)
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device) # 动作不再是float类型
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
# 更新两个Q网络
td_target = self.calc_target(rewards, next_states, dones)
critic_1_q_values = self.critic_1(states).gather(1, actions)
critic_1_loss = torch.mean(
F.mse_loss(critic_1_q_values, td_target.detach()))
critic_2_q_values = self.critic_2(states).gather(1, actions)
critic_2_loss = torch.mean(
F.mse_loss(critic_2_q_values, td_target.detach()))
self.critic_1_optimizer.zero_grad()
critic_1_loss.backward()
self.critic_1_optimizer.step()
self.critic_2_optimizer.zero_grad()
critic_2_loss.backward()
self.critic_2_optimizer.step()
# 更新策略网络
probs = self.actor(states)
log_probs = torch.log(probs + 1e-8)
# 直接根据概率计算熵
entropy = -torch.sum(probs * log_probs, dim=1, keepdim=True) #
q1_value = self.critic_1(states)
q2_value = self.critic_2(states)
min_qvalue = torch.sum(probs * torch.min(q1_value, q2_value),
dim=1,
keepdim=True) # 直接根据概率计算期望
actor_loss = torch.mean(-self.log_alpha.exp() * entropy - min_qvalue)
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# 更新alpha值
alpha_loss = torch.mean(
(entropy - target_entropy).detach() * self.log_alpha.exp())
self.log_alpha_optimizer.zero_grad()
alpha_loss.backward()
self.log_alpha_optimizer.step()
self.soft_update(self.critic_1, self.target_critic_1)
self.soft_update(self.critic_2, self.target_critic_2)
actor_lr = 1e-3
critic_lr = 1e-2
alpha_lr = 1e-2
num_episodes = 200
hidden_dim = 128
gamma = 0.98
tau = 0.005 # 软更新参数
buffer_size = 10000
minimal_size = 500
batch_size = 64
target_entropy = -1
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = SAC(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, alpha_lr,
target_entropy, tau, gamma, device)
return_list = rl_utils.train_off_policy_agent(env, agent, num_episodes,
replay_buffer, minimal_size,
batch_size)
Iteration 0: 100%|██████████| 20/20 [00:00<00:00, 148.74it/s, episode=20, return=19.700]
Iteration 1: 100%|██████████| 20/20 [00:00<00:00, 28.35it/s, episode=40, return=10.600]
Iteration 2: 100%|██████████| 20/20 [00:00<00:00, 24.96it/s, episode=60, return=10.000]
Iteration 3: 100%|██████████| 20/20 [00:00<00:00, 24.87it/s, episode=80, return=9.800]
Iteration 4: 100%|██████████| 20/20 [00:00<00:00, 26.33it/s, episode=100, return=9.100]
Iteration 5: 100%|██████████| 20/20 [00:00<00:00, 26.30it/s, episode=120, return=9.500]
Iteration 6: 100%|██████████| 20/20 [00:09<00:00, 2.19it/s, episode=140, return=178.400]
Iteration 7: 100%|██████████| 20/20 [00:15<00:00, 1.30it/s, episode=160, return=200.000]
Iteration 8: 100%|██████████| 20/20 [00:15<00:00, 1.30it/s, episode=180, return=200.000]
Iteration 9: 100%|██████████| 20/20 [00:15<00:00, 1.29it/s, episode=200, return=197.600]
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('SAC on {}'.format(env_name))
plt.show()
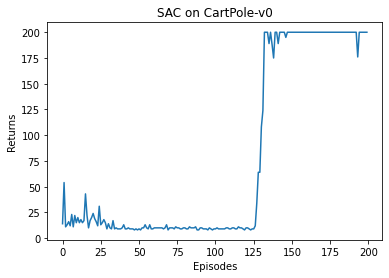
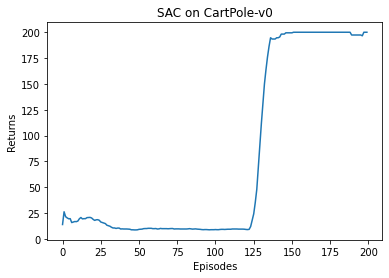
可以发现,SAC 在离散动作环境车杆下具有完美的收敛性能,并且其策略回报的曲线十分稳定,这体现出 SAC 可以在离散动作环境下平衡探索与利用的优秀性质。
14.6 小结
本章首先讲解了什么是最大熵强化学习,并通过控制策略所采取动作的熵来调整探索与利用的平衡,可以帮助读者加深对探索与利用的关系的理解;然后讲解了 SAC 算法,剖析了它背后的原理以及具体的流程,最后在连续的倒立摆环境以及离散的车杆环境中进行了 SAC 算法的代码实践。 由于有扎实的理论基础和优秀的实验性能,SAC 算法已经成为炙手可热的深度强化学习算法,很多新的研究基于 SAC 算法,第 17 章将要介绍的基于模型的强化学习算法 MBPO 和第 18 章将要介绍的离线强化学习算法 CQL 就是以 SAC 作为基本模块构建的。
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2023-04-15,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

