微软 & 麻省理工 | 实验结果表明：代码自修复能力仅存在GPT-4！GPT-3.5不具备该能力

大型语言模型（LLMs）在代码生成方面展现出了卓越的能力，但在具有挑战性的编程任务上仍然存在困难，目前使用大模型实现代码自我修复是一个比较流行的研究方法。今天给大家分享的这篇文章，作者探讨了GPT自修复在代码生成中的应用，具体研究了GPT-3.5和GPT-4在调试和修复其自动生成的代码中的效果，在此过程中，作者引入了一种名为"pass@t"的评估策略，通过对比实验发现，自我修复的有效性仅在GPT-4中可见，GPT-3.5不具备代码自修复能力。

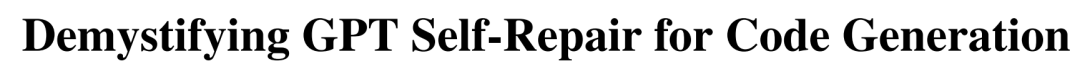
Paper：https://arxiv.org/pdf/2306.09896.pdf

背景介绍

 大型语言模型(LLM)已经被证明能够从自然语言规范中生成代码片段，但当面对复杂的编码任务时仍然存在一定的挑战，例如在编码竞赛、软件工程面试中。最新的研究工作试图利用大模型的自我修复来提高LLM在复杂编码任务场景下的性能。下图是一个典型的自我修复方法工作流。

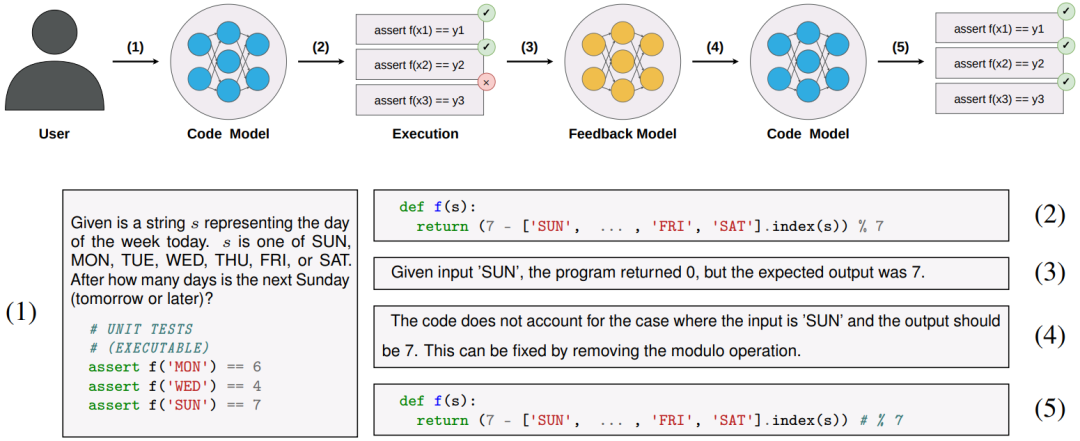
其中：

• 首先，用户需要给定一个规范，该规范包含文本提示和一组单元测试示例;
• 然后，代码生成模型根据文本提示实现代码生成，并利用单元测试示例对生成代码进行测试，如果测试失败，则将错误信息和问题代码给到反馈模型，该模型会输出代码运行失败的原因解释。
• 最后，将错误原因解释反馈给代码生成模型，进而实现代码自修复。

从表面上看，这是一个非常有吸引力的想法。它可以使系统克服解码过程中由于采样不准确而导致的错误；在修复阶段轻松合并来自符号系统（例如编译器、静态分析工具和执行引擎）的反馈；并模仿人类软件工程师编写代码的试错方式。然而，在此过程中，代码自修复的有效性不仅取决于模型生成代码的能力，而且还取决于它识别代码与任务规范有关的错误的能力。截至目前，并没有对此过程做更加细致的研究。

基于以上背景，本文作者研究了GPT-3.5和GPT-4在解决竞赛级代码生成任务时自我修复的有效性，提出一种名为pass@t的评估策略，根据从模型中采样的Token总数来权衡获得正确代码（相对于给定单元测试）的可能性。与传统的pass@k指标相比，本文评估策略能够准确地将通过自我修复获得的性能与模型在生成反馈和执行修复时所做的任何额外工作进行比较。

代码自修复过程

按照上图代码自修复流程，其主要分为四个步骤：代码生成、代码执行、反馈生成、代码自修复等。

「代码生成」给定一个规范

，代码模型

首先生成

个样本（符合独立同分布，i.d.d），每个样本用

表示，总体可表示为：

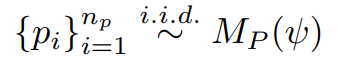
「代码执行」结合单元测试样例，对

个生成的代码样本进行回归测试。如果有样本通过了测试，那么就会停止。如果没有通过测试，将会收集测试返回的消息

，这些错误消息要么包含编译/运行时错误信息，要么包含程序输出与预期输出不同的示例输入。

「反馈生成」由于执行测试遇到的错误消息等级非常高，提供的修复信息提示也相对比较少。因此，作为中间步骤，本文使用反馈模型来对出现的问题进行更详细的解释。在此过程中，每个错误程序代码

生成的

个反馈字符串为：

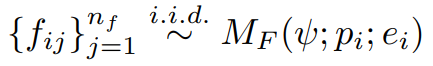
「代码修复」对于每个初始程序

和反馈

，通过代码修复模型生成

个候选修复程序代码。

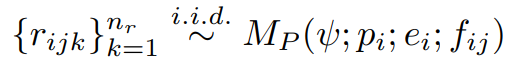
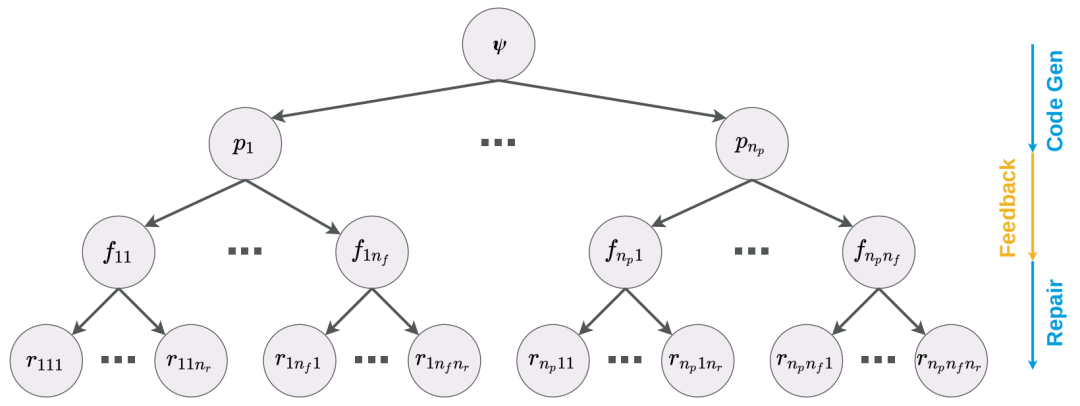
「修复树」根据上面四个过程，作者将生成的代码、反馈生成的错误字符、修复的程序代码组成的树，成为修复树，如下图所示。该树源于规范ψ，然后分支成初始程序

，每个初始程序分支成反馈

，然后修复

。

pass@t评估

由于代码自修复需要调用多个模型，并且每个模型的调用时间并不相同。因此，在这种情况下，pass@k主要是指在k个样本中获得正确程序代码的可能性，而不是比较和评估自我修复的各种超参数选择的合适度量。相反，本文将通过率作为从模型中采样的Token总数的函数来度量，本文称之为pass@t。

具体地，假设有一个数据集

和一组选定的超参数

。假设

表示一棵修复树，它是对任务

进行采样得到的，令

表示修复树中程序代码token和反馈token的总数;并且

为真当且仅当

至少有一个叶程序满足规范

中的单元测试。然后，这种超参数选择的pass@t指标被定义为您期望使用这种超参数选择生成的令牌数量的预期通过率:

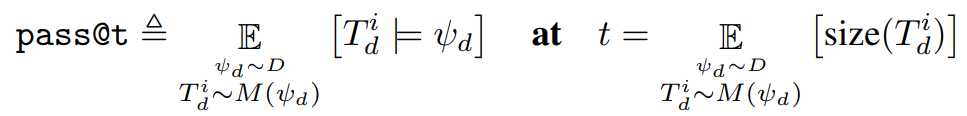
实验过程中，作者绘制了这两个变量的估计值。为了获得这些数据，首先为每个任务规范生成一个非常大的修复树，其中：

初始程序样本；

每个错误代码反馈字符串；

每个反馈字符串的修复候选。给定

的设置，然后我们从这个冻结数据集中对

个不同的修复树进行子采样（带替换）。最后，计算这

棵树的通过率和树大小的样本均值和标准差。以这种方式估计pass@t大大降低了计算成本，因为可以重用相同的初始数据集来计算

、

和

的所有各种选择的估计。

实验结果

基于APPS数据集和本文pass@t评估方法。GPT-3.5及GPT-4的代码自修复结果分别如下图所示。其中左侧子图中每个点的颜色表示初始样本的数量

，而其形状表示反馈修复样本的数量

。在右侧图中，显示了沿轴具有两个超参数的热图。

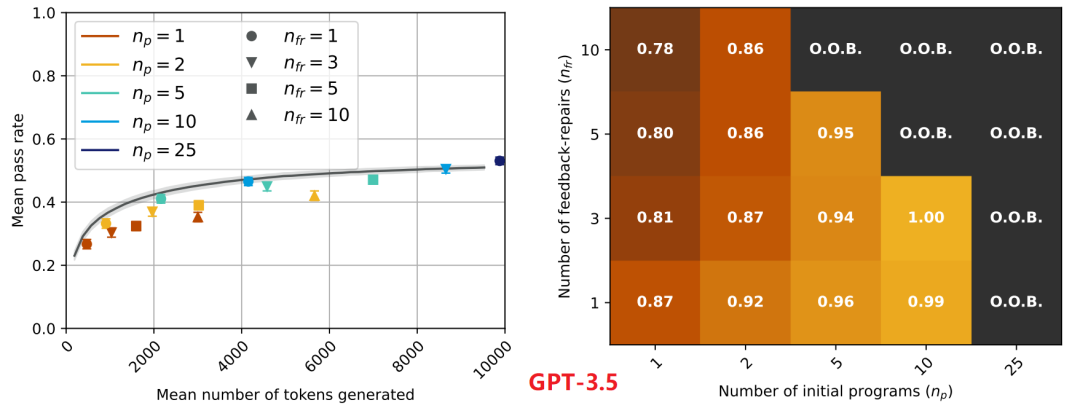
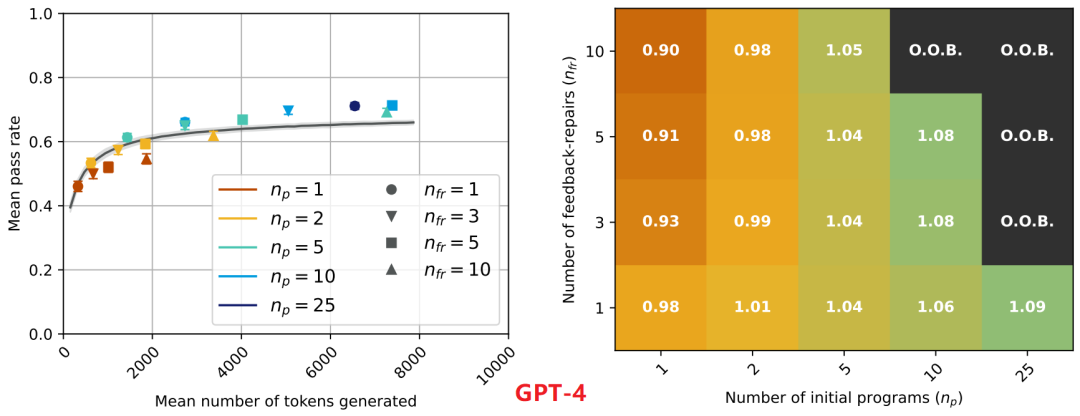
通过上图对比可以发现，GPT-3.5自我修复的通过率低于或等于基线，其代码自修复的能力有限，而GPT-4自我修复的通过率明显优于基线，其具备代码自修复能力。