斯特林公式(Stirling's approximation)
斯特林公式(Stirling’s approximation)是一条用来取n的阶乘的近似值的数学公式。
简介
斯特林公式(Stirling’s approximation)是一条用来取 n 的阶乘的近似值的数学公式。一般来说,阶乘的计算复杂度为线性。当要为某些极大的 n 求阶乘时,常见的方法复杂度不可接受。斯特林公式能够将求解阶乘的复杂度降低到对数级。而且,即使在 n 很小的时候,斯特林公式的取值已经十分准确。
公式
极限形式
证明
取对数
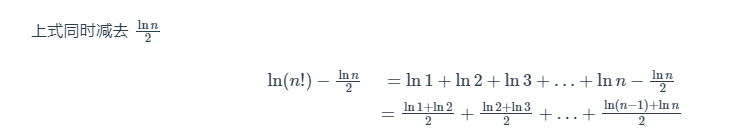
之所以构造这个形式是为了构造积分梯形法则,考虑函数 f(x)=\ln x ,在其中做梯形面积累加:

令梯形面积和为 G(n)=\ln (n !)-\frac{\ln n}{2}
令积分面积和为:

为

即
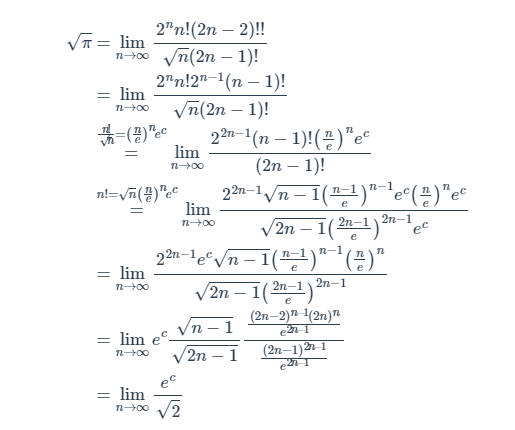
因此
得斯特林公式, 时
斯特林公式的精度
斯特林公式在 n 不大的时候已经很精准了,我们尝试计算其精度
上界
根据上文的梯形法则计算原理,结合\ln x 函数二阶导为负数的事实,可以知道 [1,n] 内梯形面积和永远小于原始函数积分面积,因此有:

下界
考虑传统的 积分放缩法

可以得到:
但是由这个不等式推出的结论不够紧致,为了得到更紧致的估计,我们将所有的矩形向右平移 0.5

这样对于每个矩形区域,矩形面积和在该矩形横坐标覆盖范围内的积分的大小关系取决于图中同一个矩形内 蓝色 和 绿色 面积的大小关系。
由于 \ln x 的二阶导为负数,以矩形中点为界,向左、向右的两个面积区域中,距离中点距离相等的两个点来说,蓝色区域内的高度会大于绿色区域内的高度。
因此对于每个矩形,形成的蓝色面积要大于绿色面积,因此矩形面积大于积分面积,有:

参考资料
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2023-11-14,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录


