深度学习500问——Chapter03：深度学习基础（2）

3.3 超参数

3.3.1 什么是超参数

超参数：在机器学习的上下文中，超参数是在开始学习过程之前设置值的参数，而不是通过训练得到的参数数据。通常情况下，需要对超参数进行优化，给学习机选择一组最优超参数，以提高学习的性能和效果。

超参数通常在于：

1. 定义关于模型的更高层次的概念，如复杂性或学习能力。
2. 不能直接从标准模型培训过程中的数据中学习，需要预先定义。
3. 可以通过设置不同的值，训练不同的模型和选择更好的测试值来决定。

超参数具体来讲比如算法中的学习率（learning rate）、梯度下降法迭代的数量（iterations）、隐藏层数目（hidden layers）、隐藏层单元数目、激活函数（activation function）都需要根据实际情况来设置，这些数字实际上控制了最后的参数和的值，所以它们被称作超参数。

3.3.2 如何寻找超参数的最优值

在使用机器学习算法时，总有一些难调的超参数。例如权重衰减大小，高斯核宽度等等。这些参数需要人为设置，设置的值对结果产生较大影响。常见设置超参数的方法有：

1. 猜测和检查：根据经验或直觉，选择参数，一直迭代。
2. 网格搜素：让计算机尝试在一定范围内均匀分布的一组值。
3. 随机搜素：让计算机随机挑选一组值。
4. 贝叶斯优化：使用贝叶斯优化超参数，会遇到贝叶斯优化算法本身就需要很多参数的困难。
5. MITIE方法，初始猜测的前提下进行局部优化。它使用BOBYQA算法，并有一个精心选择的起始点。由于BOBYQA只寻找最近的局部最优解，所以这个方法是否成功很大程度上取决于是否有一个好的起点。在MITIE的情况下，我们知道一个好的起点，但这不是一个普遍的解决方案，因为通常你不会知道好的起点在哪里。从好的方面来说，这种方法非常适合寻找局部最优解。稍后我会再讨论这一点。
6. 最新提出的LIPO的全局优化方法。这个方法没有参数，而且经验证比随机搜索方法好。

3.3.3 超参数搜索一般过程

超参数搜索一般过程：

1. 将数据集划分为训练集、验证集和测试集。
2. 在训练集上根据模型的性能指标对模型参数进行优化。
3. 在验证集上根据模型的性能指标对模型的超参数进行搜索。
4. 步骤2和步骤3交替迭代，最终确定模型的参数和超参数，在测试集中验证评价模型的优劣。

其中，搜索过程需要搜索算法，一般有：网格搜索、随机搜索、启发式智能搜索、贝叶斯搜索。

3.4 激活函数

3.4.1 为什么需要非线性激活函数

为什么需要激活函数？

1. 激活函数对模型学习、理解非常复杂和非线性的函数具有重要作用。
2. 激活函数可以引入非线性因素。如果不使用激活函数，则输出信号仅是一个简单的线性函数。线性函数是一个一级多项式，线性方程的复杂度有限，从数据中学习复杂函数映射的能力很小。没有激活函数，神经网络将无法学习和模拟其他复杂类型的数据，例如图像、视频、音频、语音等。
3. 激活函数可以把当前特征空间通过一定的线性映射转换到另一个空间，让数据能够更好的被分类。

为什么激活函数需要非线性函数？

1. 假若网络中全部是线性部件，那么线性的组合还是线性，与单独一个线性分类器无异。这样就做不到用非线性来逼近任意函数。
2. 使用非线性激活函数，以便使网络更加强大，增加它的能力，使它可以学习复杂的事物，复杂的表单数据，以及表示输入输出之间非线性的复杂的任意函数映射。使用非线性激活函数，能够从输入输出之间生成非线性映射。

3.4.2 常见的激活函数及图像

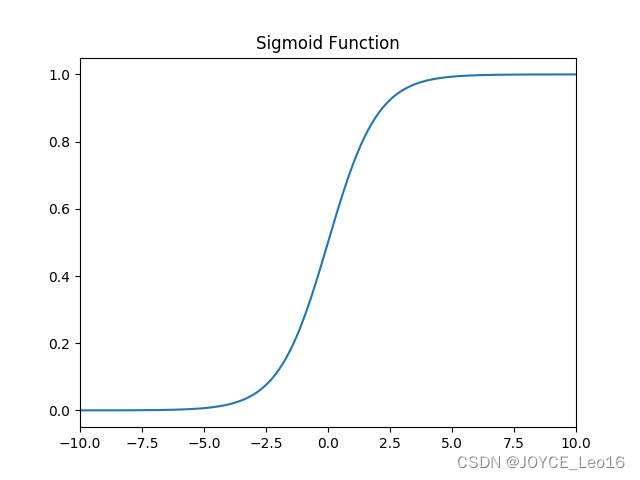
1. sigmoid 激活函数

函数的定义为：

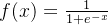
，其值域为

。

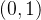
函数图像如下：

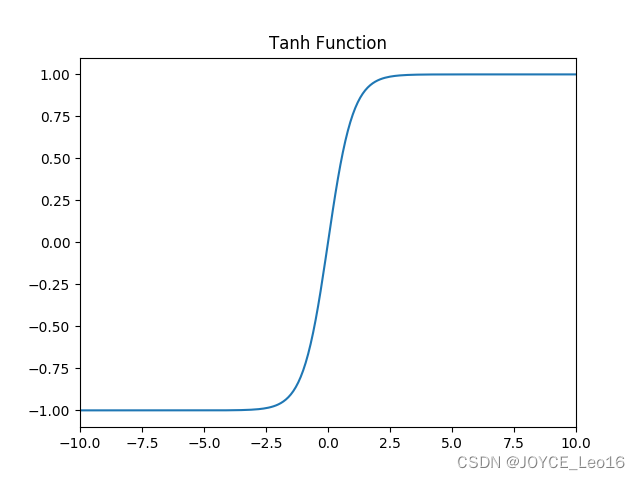
2. tanh 激活函数

函数的定义为：

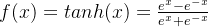
，值域为

。

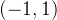
函数图像如下：

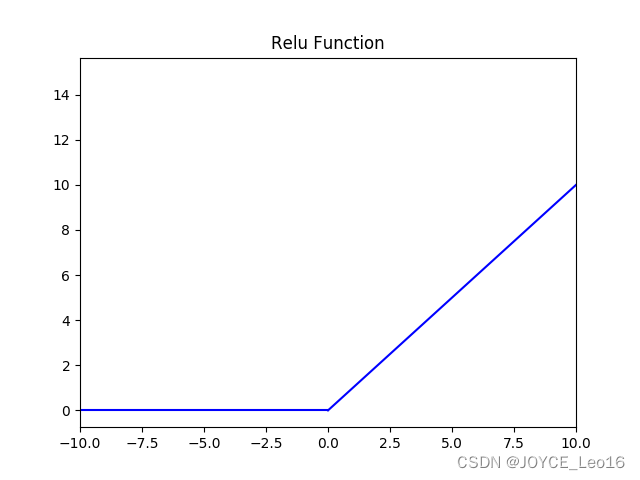
3. Relu 激活函数

函数的定义为：

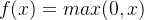
，值域为

[0,+∞)。

函数图像如下：

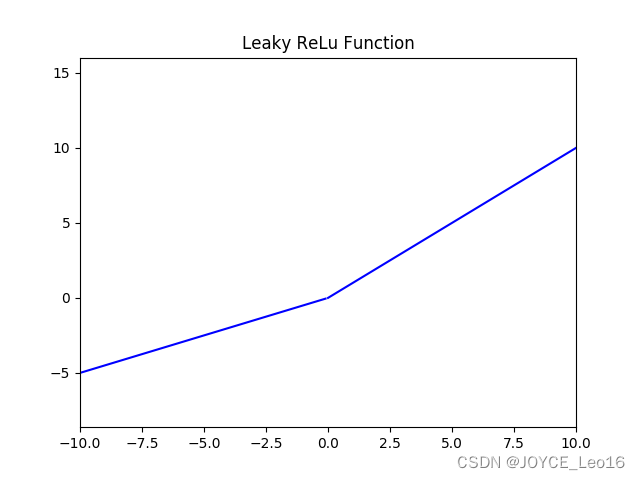
4. Leak Relu 激活函数

函数定义为：

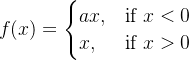
，值域为 (-∞,+∞)。

函数图像如下（

）：

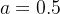
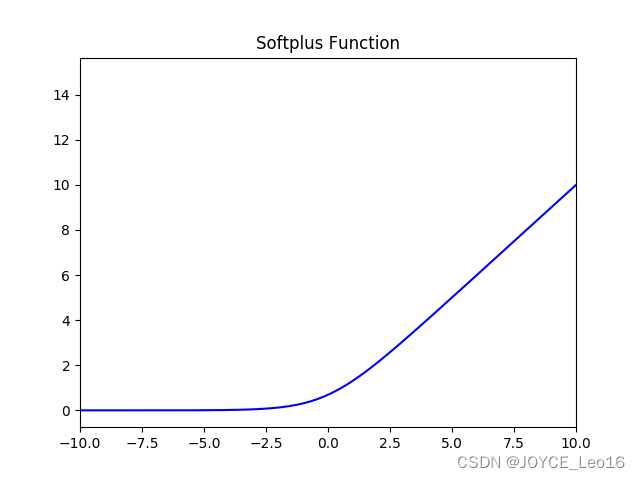
5. SoftPlus 激活函数

函数的定义为：

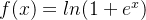
，值域为 (0,+∞)。

函数图像如下：

6. softmax 激活函数

函数定义为：

。

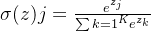
Softmax 多用于多分类神经网络输出。

3.4.3 常见激活函数的导数计算

对常见激活函数，导数计算如下：

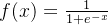
3.4.4 激活函数有哪些性质

1. 非线性：当激活函数是非线性的，一个两层的神经网络就可以基于上逼近所有的函数。但如果激活函数是恒等激活函数的时候，即

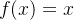
，就不能满足这个性质，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的。

1. 可微性：当优化方法是基于梯度的时候，就体现了该性质。
2. 单调性：当激活函数是单调的时候，单层网络能够保证是凸函数。

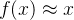
：当激活函数满足这个性质的时候，如果参数的初始化是随机的较小值，那么神经网络的训练将会很有高效；如果不满足这个性质，那么就需要详细地去设置初始值。

1. 输出值的范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况下，一般需要更小的 Learning Rate。

3.4.5 如何选择激活函数

选择一个适合的激活函数并不容易，需要考虑很多因素，通常的做法是，如果不确定哪一个激活函数效果更好，可以把它们都试试，然后在验证集或者测试集上进行评价。然后看哪一种表现更好，就去使用它。

以下是常见的选择情况：

1. 如果输出是0、1值（二分类问题），则输出层选择 sigmoid 函数，然后其他的所有的单元都选择 Relu 函数。
2. 如果在隐藏层上不确定使用哪个激活函数，那么通常会使用 Relu 激活函数。有时，也会使用 tanh 激活函数，但 Relu 的一个优点是：当是负值的时候，导数等于0。
3. sigmoid 激活函数：除了输出层是一个二分类问题基本不会用它。
4. tanh 激活函数：tanh是非常优秀的，几乎适合所有场合。
5. Relu 激活函数：最常见的默认函数，如果不确定用哪个激活函数，就使用 Relu 或 Leaky Relu，再去尝试其他的激活函数。
6. 如果遇到了一些死的神经元，我们可以使用 Leaky ReLU 函数。

3.4.6 使用 ReLu 激活函数的优点

1. 在区间变动很大的情况下，Relu 激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个 if-else 语句，而 sigmoid 函数需要进行浮点四则运算，在实践中，使用Relu激活函数神经网络通常会比使用 sigmoid或者 tanh激活函数学习的更快。
2. sigmoid 和 tanh 函数的导数在负饱和区的梯度都接近于0，这会造成梯度弥散，而Relu 和 Leaky Relu函数大于0部分都为常数，不会产生梯度弥散现象。
3. 需注意，Relu进入负半区的时候，梯度为0，神经元此时不会训练，产生所谓的稀疏性，而Leaky Relu不会产生这个问题。

3.4.7 什么时候可以用线性激活函数

1. 输出层，大多使用线性激活函数。
2. 在隐含层可能会使用一些线性激活函数。
3. 一般用到的线性激活函数很少。

3.4.8 怎样理解 Relu（<0时）是非线性激活函数

Relu激活函数图像如下：

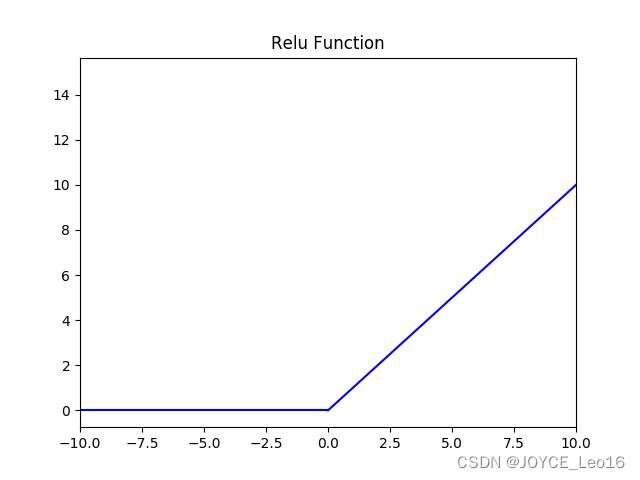
根据图像可以看出具有如下特点：

1. 单侧抑制；
2. 相对宽阔的兴奋边界；
3. 稀疏激活性；

ReLU函数从图像上看，是一个分段线性函数，把所有的负值都变为0，而正值不变，这样就成为单侧抑制。

因为有了这单侧抑制，才使得神经网络中的神经元也具有了稀疏激活性。

稀疏激活性：从信号方面来看，即神经元同时只对输入信号的少部分选择性响应，大量信号被刻意的屏蔽了，这样可以提高学习的精度，更好更快地提取稀疏特征。当

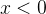
时，ReLU硬饱和，而当

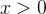
时，则不存在饱和问题。ReLU能够在

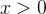
时保持梯度不衰减，从而缓解梯度消失问题。

3.4.9 Softmax 定义及作用

Softmax是一种形如下式的函数：

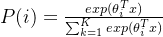
其中，

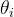
和

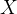
是列向量，

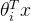
可能被换成函数关于

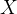
的函数

。

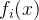
通过softmax函数，可以使得

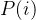
的范围在[0,1]之间。在回归和分类问题中，通常

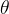
是待求参数，通过寻找使得

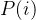
最大的

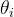
作为最佳参数。

但是，使得范围在 [0,1] 之间的方法有很多，为啥要在前面加上以

的幂函数的形式呢？参考 logistic函数：

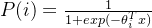
，这个函数的作用就是使得

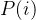
在负无穷到0的区间趋向于0，在0到正无穷的区间趋向1。同样 softmax函数加入了

的幂函数正是为了两极化：正样本的结果将趋近于1，而负样本的结果趋近于0。这样为多类别提供了方便（可以把

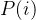
看作是样本属于类别的概率）。可以说，Softmax函数就是 logistic函数的一种泛化。

softmax函数可以把它的输入，通常被称为 logits 或者 logit scores，处理成0到1之间，并且能够把输出归一化到和为1。这意味着 softmax函数与分类的概率分布等价。它是一个网络预测多分类问题的最佳输出激活函数。

3.4.10 Softmax函数如何应用于多分类

softmax用于多分类过程，它将多个神经元的输出，映射到（0，1）区间内，可以看成概率来理解，从而来进行多分类。

假设我们有一个数组，

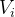
表示

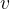
中的第

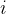
个元素，那么这个元素的 softmax 值就是：

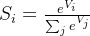
从下图看，神经网络中包含了输入层，然后通过两个特征层处理，最后通过softmax分析器就能得到不同条件下的概率，这里需要分成三个类别，最终会得到

的概率值。

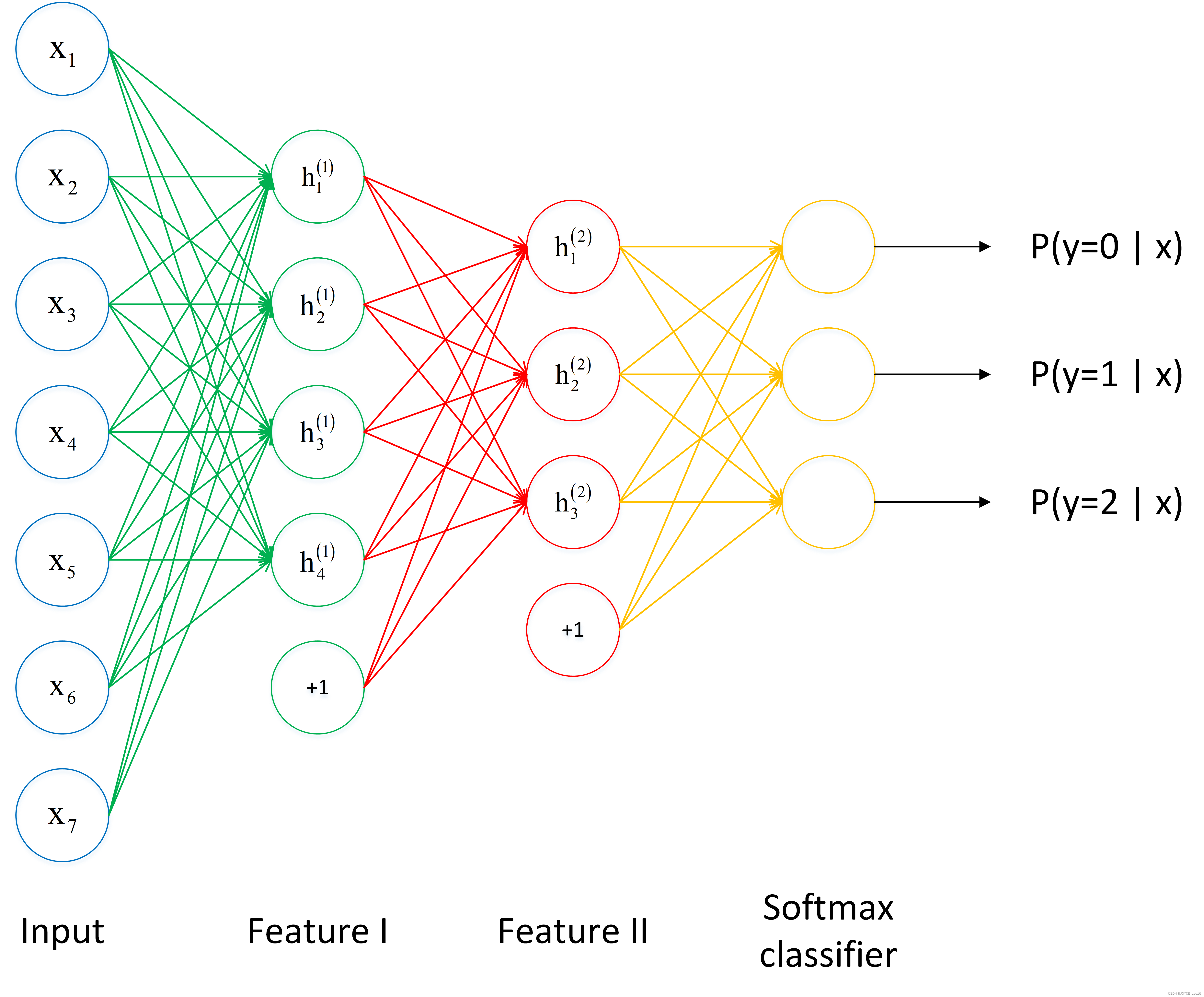
继续看下面的图，三个输入通过 softmax 后得到一个数组

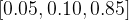
，这就是 soft 的功能。

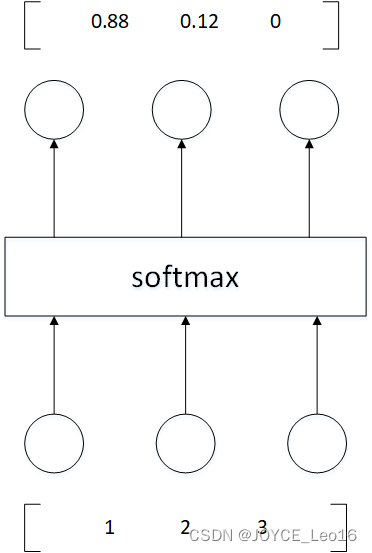
更形象的映射过程如下图所示：

softmax直白来说就是将原来输出是

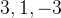
通过 softmax函数一作用，就映射成为（0，1）的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！

3.4.11 交叉熵代价函数定义及其求导推导

神经元的输出就是

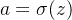
，其中

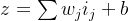
就是输入的带权和。

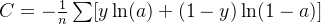
其中，

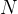
是训练数据的总数，求和是在所有的训练输入

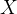
上进行的，

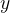
是对应的目标输出。

表达式是否解决学习缓慢的问题并不明显。实际上，甚至将这个定义看作是代价函数也不是显而易见的！在解决学习缓慢前，我们来看看交叉熵为何能够解释成一个代价函数。

将交叉熵看作是代价函数有两点原因：

第一，它是非负的，C>0。可以看出：式子中的求和中的所有独立的项都是负数的，因为对数函数的定义域是(0,1)，并且求和前面有一个负号，所以结果是非负。

第二，如果对于所有的训练输入x，神经元实际的输出接近目标值，那么交叉熵将接近0。

假设在这个例子中，y=0而

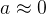
。这是我们想要得到的结果。我们看到公式中的第一个项就消去了，因为y=0，而第二项实际上就是− ln(1 − a) ≈ 0。反之，y = 1 ⽽ a ≈ 1。所以在实际输出和⽬标输出之间的差距越⼩，最终的交叉熵的值就越低了。（这里假设输出结果不是0，就是1，实际分类也是这样的）。

​ 综上所述，交叉熵是非负的，在神经元达到很好的正确率的时候会接近 0。这些其实就是我们想要的代价函数的特性。其实这些特性也是⼆次代价函数具备的。所以，交叉熵就是很好的选择了。但是交叉熵代价函数有⼀个⽐⼆次代价函数更好的特性就是它避免了学习速度下降的问题。为了弄清楚这个情况，我们来算算交叉熵函数关于权重的偏导数。我们将a={\varsigma}(z)代⼊到 公式中应⽤两次链式法则，得到：

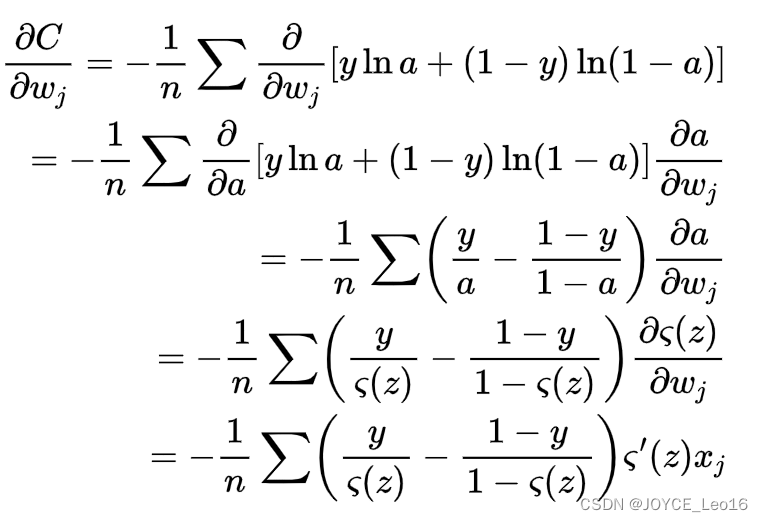
​ 根据

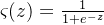
的定义，和⼀些运算，我们可以得到

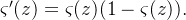
。化简后可得：

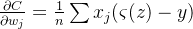
​ 这是⼀个优美的公式。它告诉我们权重学习的速度受到

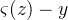
，也就是输出中的误差的控制。更⼤的误差，更快的学习速度。这是我们直觉上期待的结果。特别地，这个代价函数还避免了像在⼆次代价函数中类似⽅程中

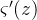
导致的学习缓慢。当我们使⽤交叉熵的时候，

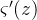
被约掉了，所以我们不再需要关心它是不是变得很小。这种约除就是交叉熵带来的特效。实际上，这也并不是⾮常奇迹的事情。我们在后⾯可以看到，交叉熵其实只是满⾜这种特性的⼀种选择罢了。

​ 根据类似的方法，我们可以计算出关于偏置的偏导数。我这⾥不再给出详细的过程，你可以轻易验证得到：

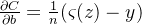
​ 再⼀次, 这避免了⼆次代价函数中类似

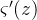
项导致的学习缓慢。

3.4.12 为什么Tanh收敛速度比Sigmoid快

首先看如下两个函数的求导：

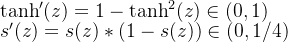
由上面两个公式可知tanh(x)梯度消失的问题比sigmoid轻，所以Tanh收敛速度比Sigmoid快。

注：梯度消失（gradient vanishing）或者爆炸（gradient explosion）是激活函数以及当前权重耦合产生的综合结果：​ 设任意激活函数为

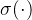
，k+1层网络输出为

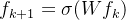
，求导得到

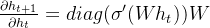
。可见求导结果同时会受到权重

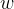
和激活函数的导数

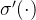
的影响，以sigmoid函数

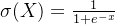
为例，其导数为

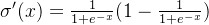
，其值恒大于零小于1，用链式法则求梯度回传时连续相乘使得结果趋于0，但是如果权重

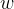
是较大的数值，使得

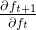
相乘结果大于1，则梯度回传时连续相乘则不会发生梯度消失。 综上，在讨论激活函数收敛速度或与梯度消失或者爆炸相关时，应同时考虑当前权重

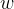
数值的影响。

3.4.13 内聚外斥 - Center Loss

在计算机视觉任务中, 由于其简易性, 良好的表现, 与对分类任务的概率性理解, Cross Entropy Loss (交叉熵代价) + Softmax 组合被广泛应用于以分类任务为代表的任务中. 在此应用下, 我们可将其学习过程进一步理解为: 更相似(同类/同物体)的图像在特征域中拥有“更近的距离”, 相反则”距离更远“. 换而言之, 我们可以进一步理解为其学习了一种低类内距离(Intra-class Distance)与高类间距离(Inter-class Distance)的特征判别模型. 在此Center Loss则可以高效的计算出这种具判别性的特征. 不同于传统的Softmax Loss, Center Loss通过学习“特征中心”从而最小化其类内距离. 其表达形式如下:

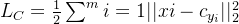
其中

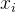
表示FCN(全连接层)之前的特征,

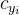
表示

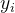
个类别的特征中心,

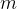
表示mini-batch的大小. 我们很清楚的看到

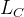
的终极目标为最小化每个特征与其特征中心的方差, 即最小化类内距离. 其迭代公式为:

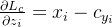
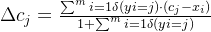
其中，

。

结合Softmax, 我们可以搭配二者使用, 适当平衡这两种监督信号. 在Softmax拉开类间距离的同时, 利用Center Loss最小化类内距离. 例如:

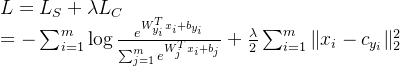
即便如此, Center Loss仍有它的不足之处: 其特征中心为存储在网络模型之外的额外参数, 不能与模型参数一同优化. 这些额外参数将与记录每一步特征变化的自动回归均值估计(autoregressive mean estimator)进行更迭. 当需要学习的类别数量较大时, mini-batch可能无力提供足够的样本进行均值估计. 若此Center Loss将需要平衡两种监督损失来以确定更迭, 其过程需要一个对平衡超参数的搜索过程, 使得其择值消耗昂贵.