双目视觉理论篇
相机模型与四种参考坐标系
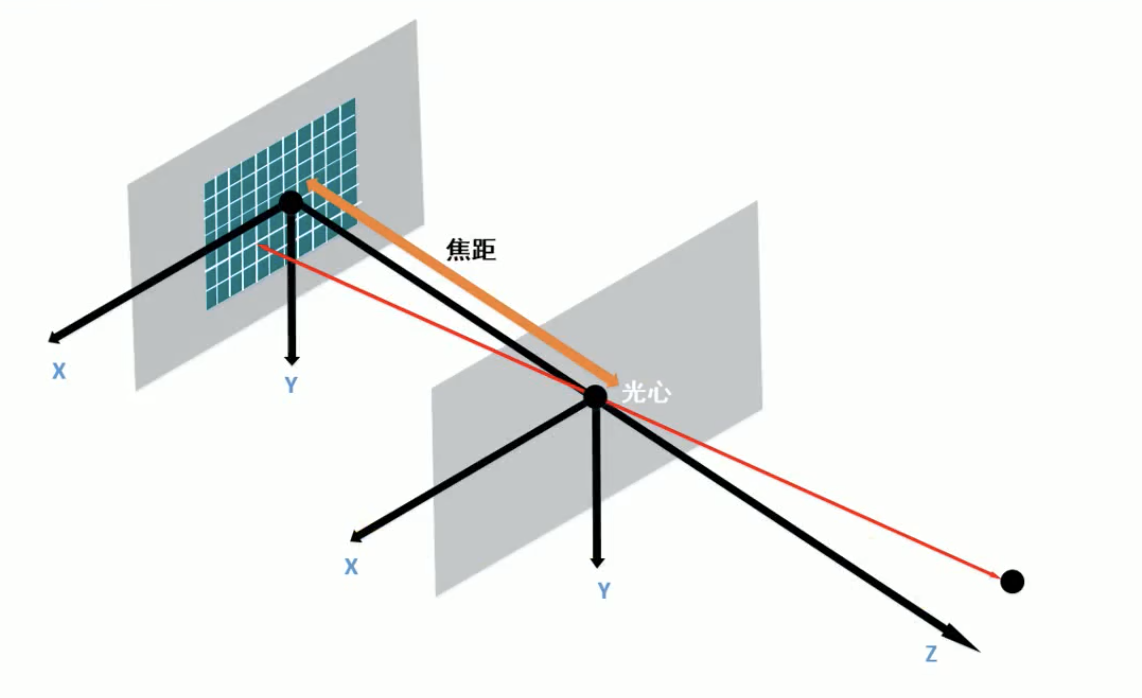
上图中右下角的黑点是真实世界的一个点，最左边的灰色部分是一张数字照片，称为像平面，单位为毫米(mm)。青色的格子则是像平面中一个一个的像素。我们现在需要知道的是黑色的点是如何变成像平面中的一个像素。中间的灰色部分是相机的透镜，而该部分中心点称为光心。真实世界的黑点会经过各种模型(线性或非线性的)，通过光心在像平面中得到一个像素点。
像素坐标系
我们会在像平面中建立一个直角坐标系，称为像素坐标系。
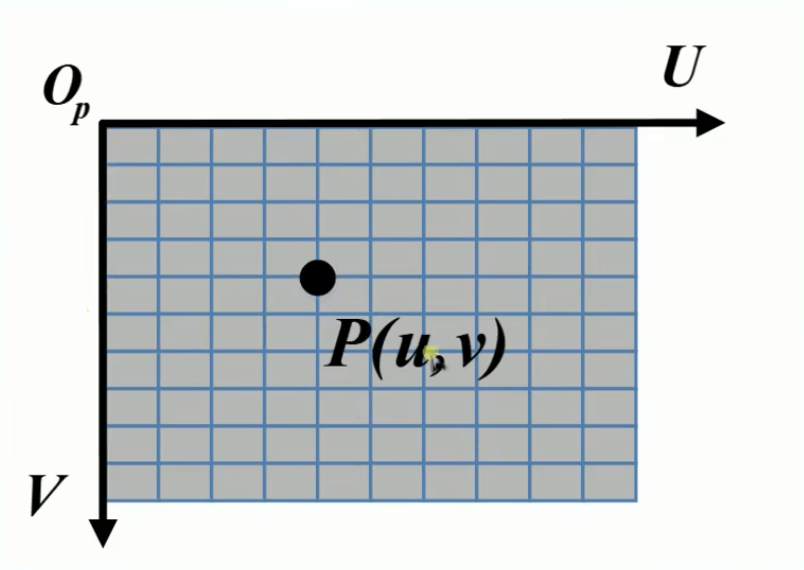
整个像平面是一个高*宽(H*W)的数组，图像的左上角定义为原点(O_p)，横轴为U，纵轴为V，该坐标系中的一点P(u,v)代表第u列，第v行的一个像素。但是这里会有一个问题，那就是像素坐标系是以像素为单位的，而图像坐标系是以mm为单位的，它们之间存在一个转换关系。
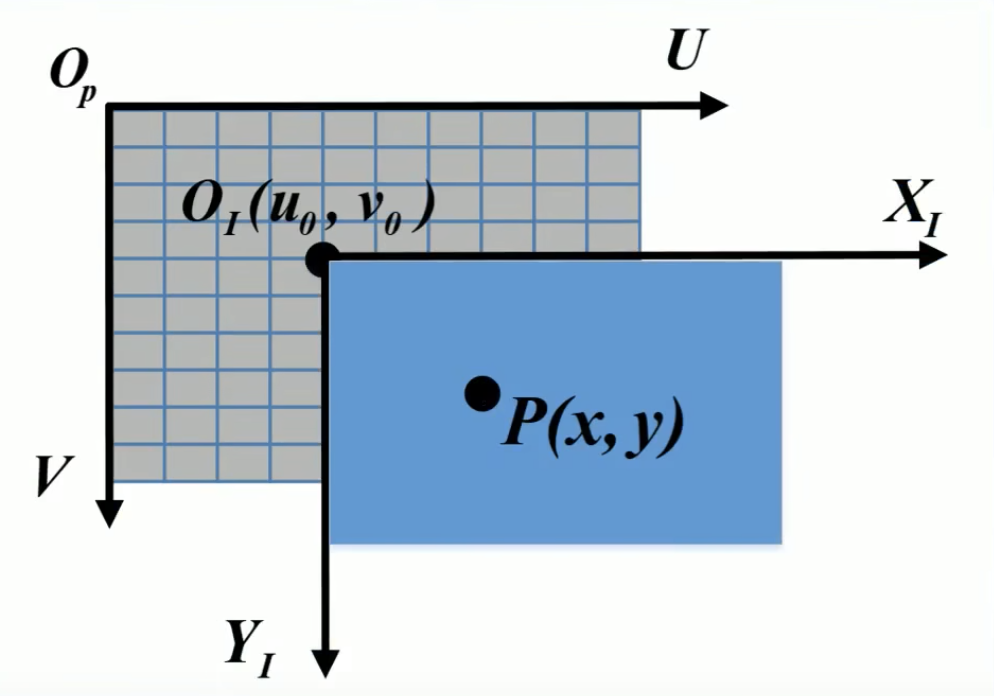
上图中(O_p)是像素坐标系的原点，(O_I(u_0,v_0))是图像坐标系的原点，它是像素坐标系的中点，但有时候也会发生一些偏离，不完全在中点上，它的单位既为mm。当我们有了P(x,y)在图像坐标系上的坐标以后就可以得到像素坐标系的坐标，转换关系如下
- (u={x\over dx}+u_0)
- (v={y\over dy}+v_0)
上式中x、y是P点在图像坐标系中的坐标，单位为mm，dx、dy是一个像素的宽度和高度，单位也为mm，(u_0、v_0)是图像坐标系原点在像素坐标系中的坐标，单位是像素。上式用矩阵运算的形式来表达为
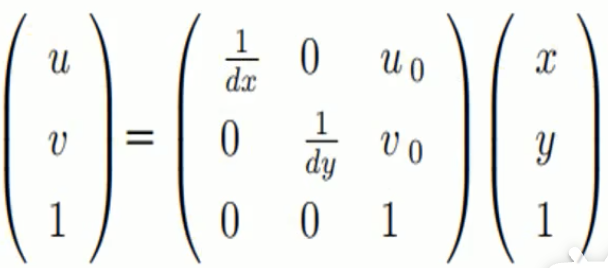
左边的部分是P点在像素坐标系中的坐标，最右边的部分是P点在图像坐标系中的坐标，中间的矩阵则为图像坐标系坐标变换为像素坐标系坐标的变换矩阵。
相机坐标系
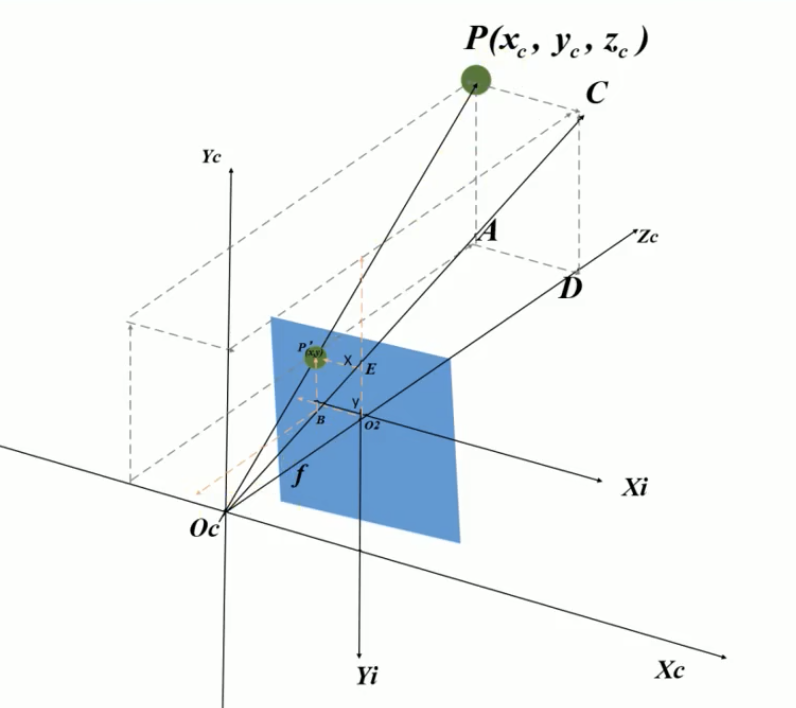
上图中的蓝色块为像平面的坐标系，(O_c)是相机坐标系的原点，(Y_c)是纵轴，(X_c)是横轴，(Z_c)是深度轴，也就是说相机坐标系是一个空间三维坐标系。(P(x_c,y_c,z_c))是真实世界的一个点在相机坐标系中的坐标，
(PO_c)与像平面相交于P'，A是P点在(X_cZ_c)平面上的投影，其坐标即为(A(x_c,0,z_c))，(AO_c)与像平面相交于B，P'B=y，那么很明显
(△PO_cA∽△P'O_cB) (三角形(PO_cA)与三角形(P'O_cB)相似) => ({y_c\over y}={PO_c\over P'O_c}={AO_c\over BO_c})
C是P点在(Y_cZ_c)平面上的投影，其坐标即为(C(0,y_c,z_c))，(CO_c)与像平面相交于E，P'E=x，那么很明显
(△PO_cC∽△P'O_cE) => ({x_c\over x}={PO_c\over P'O_c}={CO_c\over EO_c})
D是P点在(Z_c)轴上的投影，其坐标即为(D(0,0,z_c))，(DO_c)与像平面相交于像平面坐标系原点(O_I)，(O_cO_I=f)，(EO_I=y)，这个f我们称为焦距，那么很明显
(△DO_cC∽△O_IO_cE) => ({z_c\over f}={y_c\over y}={CO_c\over EO_c})
由以上的关系，我们可以得到
- ({x_c\over x}={z_c\over f}) => (x={fx_c\over z_c})
- ({y_c\over y}={z_c\over f}) => (y={fy_c\over z_c})
这里的x,y就是P点在像平面的图像坐标系中成像的坐标。用矩阵乘法来表示就为
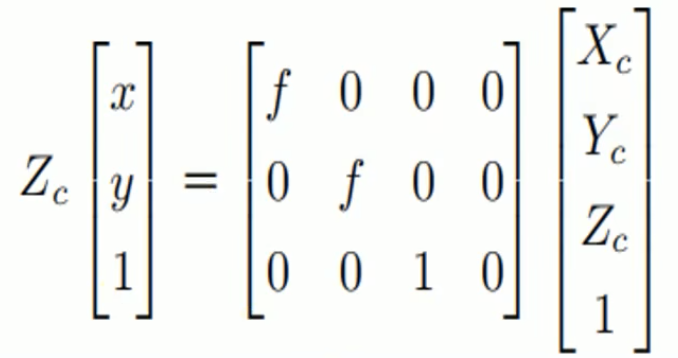
左边的x,y就是P点在像平面成像的图像坐标系中的坐标，单位为mm，最右边的(X_c、Y_c、Z_c)就是P点在相机坐标系中的坐标。再转为像素坐标系就有
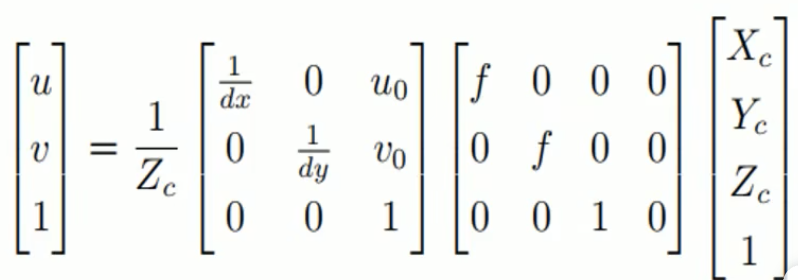
就得到最终像素坐标系中的坐标(u,v)。当然也可以简化为
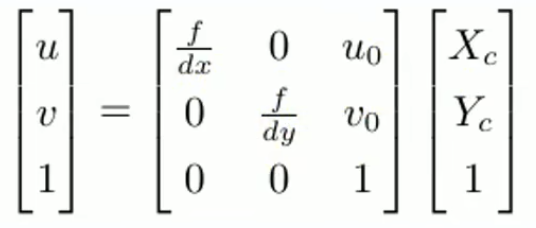
世界坐标系
为了知道相机在三维空间中的坐标，因此我们还需要引入一个世界坐标系，相机坐标系到世界坐标系的变换可以看作是刚体变换，由旋转和平移决定。对于旋转因子，我们可以将刚体在三维空间的三维旋转看作是三个方向上的二维旋转：(有关三维旋转的内容可以参考机械臂运动学整理 中的旋转矩阵与转角)
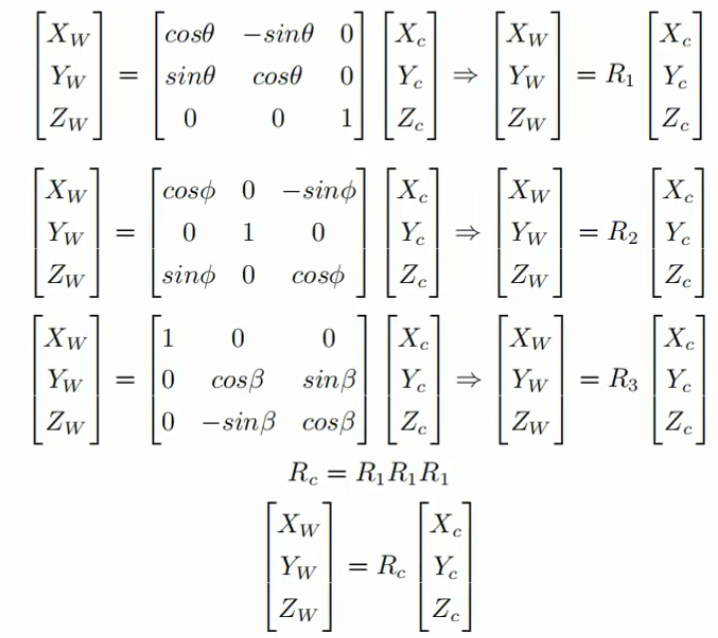
上式中的第一个式子表示相机坐标系围绕相机坐标系的自己的Z轴逆时针进行旋转了θ角得到了P点在新的相机坐标系中的坐标((X_W,Y_W,Z_W))；第二个式子表示相机坐标系围绕相机坐标系的自己的Y轴逆时针进行旋转了φ角得到了P点在新的相机坐标系中的坐标((X_W,Y_W,Z_W))；第三个式子表示相机坐标系围绕相机坐标系的自己的X轴逆时针进行旋转了β角得到了P点在新的相机坐标系中的坐标((X_W,Y_W,Z_W))。其中(R_1、R_2、R_3)分别是这三种旋转的旋转矩阵。
第四个式子表示(这里的(R_c)有问题，改为(R_c=R_1R_2R_3))依次围绕X、Y、Z轴旋转β、φ、θ角后得到最终的P点在新的相机坐标系中的坐标((X_W,Y_W,Z_W))。
以上是旋转的部分，那么对于平移因子，我们可以把刚体在三维空间的三维平移分解到三个方向上的一维向量平移：
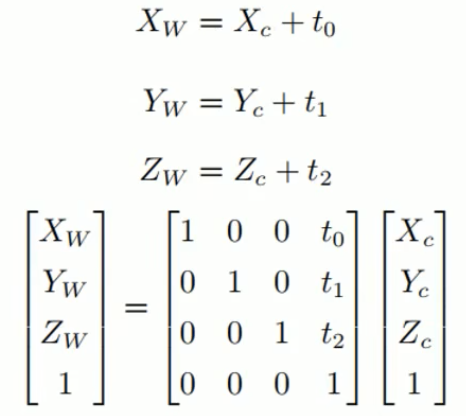
上面的式子中，(t_0)为相机坐标系沿着相机坐标系自己的X轴移动的距离； (t_1)为相机坐标系沿着相机坐标系自己的Y轴移动的距离； (t_2)为相机坐标系沿着相机坐标系自己的Z轴移动的距离。最后一个式子就是该变换的矩阵运算表示。
整合旋转与平移就有
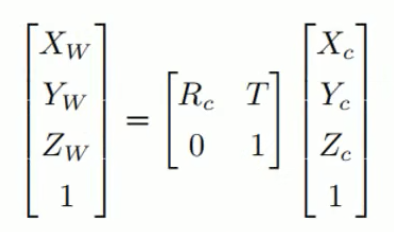
其中(R_c)是3*3的旋转矩阵，T是3*1的平移向量。最后可以得出从世界坐标系到像素坐标系的变换
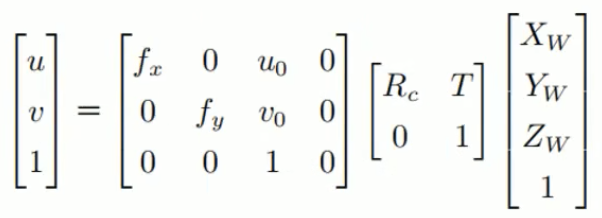
其中(f_x、f_y)为X和Y方向的坐标尺度因子，为焦距f与dx、dy的比值，即为(f_x={f\over dx})、(f_y={f\over dy})。
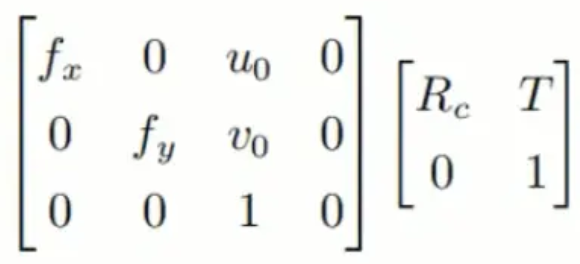
的结合矩阵称为投影矩阵，又叫M矩阵。
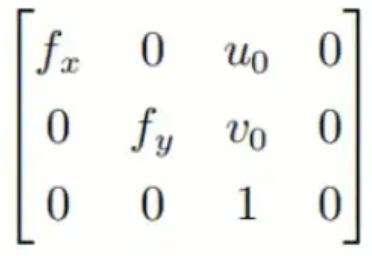
叫(M_1)矩阵，又叫内参矩阵，由相机出厂确定；
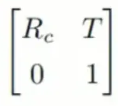
叫(M_2)矩阵，又叫外参矩阵，由相机相对于世界坐标系的方位决定。我们确定M矩阵的过程称为摄像机的标定。