Prometheus 指标值不准:是 feature,还是 bug?
Prometheus 指标值不准:是 feature,还是 bug?

引子
有一天,你打算试用 Prometheus,监控你的业务系统。
你来到腾讯云,仅需几次点击,指标便从四面八方来,汇聚成 Grafana 上的优雅曲线。
“不愧是云原生监控一哥,容器集成十分顺滑!交给云托管则更省心,连云产品也一键监控了。”
手握丰富的 Grafana 大盘,和适时的告警通知,你深感满意。

然而,没过多久,你发现不对劲:
——“32 核的 CPU,监控出来是 44.3 核?”
——“P99 百分位的值,竟比最大值还高?”
——”用不同时间范围计算 rate,出来的曲线天壤之别?“
——……

你搜索全网、询问 ChatGPT 老师、向腾讯云提工单,得到的答复干脆而统一:“Prometheus 的指标值,并非 100% 准确”。
你刨根问底,却碰上“外推”、“插值”、“窗口对齐”……等晦涩的概念。于是,你跳过解题步骤,直接背诵了答案:“Prometheus 的指标值,并非 100% 准确”。
然而,一些灵魂拷问在你脑中浮现:
——既然大家都知道它不准,为何人人还都安利它?
——现在我也知道它不准了,还值得继续用下去吗?

以上内容,纯属虚构;如有雷同,那必然是关于 Prometheus 的“谜团”太多,而“解谜”太少。
而本文正打算以一种不烧脑、能秒懂的方式,分析一些最常见的案例。
概述
长话短说,结论先行:Prometheus 指标值不准的“怪现象”,其实是在下面的“不可能三角”中,做出了取舍——为保全效率和可用性,舍弃了精度:
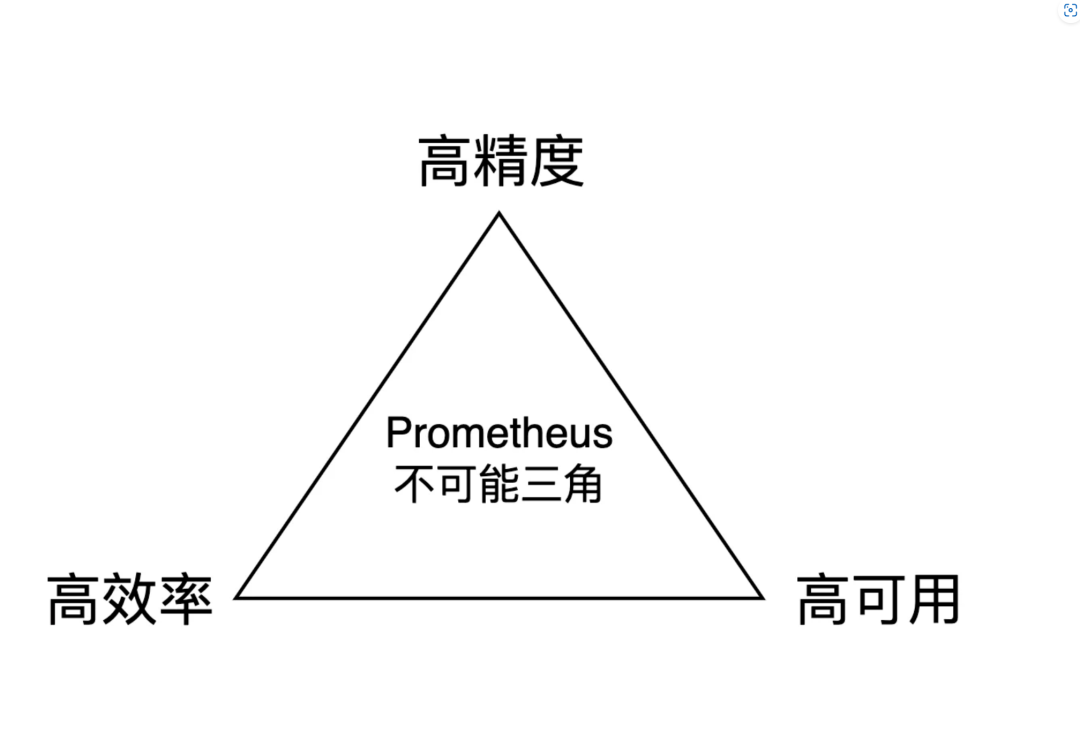
为何精度会被 Prometheus 舍弃?
归根结底,在可观测的世界里,metrics(指标)、log(日志)、trace(调用链) 三足鼎立。
而 Prometheus 所在的 metrics(指标) 领域,其目标是诊断整体健康状况,其手段通常是对原始数据先采样、再聚合,利用有限的信息,分析变化趋势;而并非像 log(日志)那样,翔实精确、事无巨细地,记录每一桩事件、每一条原始数据。
我们不妨用心脏监测来做类比:

- metrics(指标)好似运动手表:24小时采样心率,并在心率超限时告警;
- log(日志)好似详细体检:输出厚厚一沓严密、精确的权威报告;
- trace(调用链)好似血管灌注:哪段血管堵了,只需看灌注造影,一目了然。
如此看来,运动手表监测心率虽不精确,但胜在方便高效:不用跑到医院,就能 24 小时持续监控,还能自行设置告警阈值。在日常观测健康趋势方面,已然十分够用了。
除了 metrics 领域自身的特性,Prometheus 毕竟处在一个条件有限的真实世界,它还要随时面临以下困难:
- 自身硬件有限:不敢拼命计算,不敢无限存储;
- 采样统计的局限性:稀稀拉拉、分布未知的样本;
- 分布式的局限性:丢数据的网络、不靠谱的对端;
- ……
Prometheus 需要在上述限制下,交出 not perfect、但是 good enough 的指标。于是就有了下述设计:
- 单次采样不重要,多次采样组成的时间序列才重要。所以,单次采样受阻,是可以无需重试、直接丢弃的。
- 单点数值不重要,多点数值汇聚的变化趋势才重要。所以,单点数值是可以“无中生有”、"脑补"估算的。
接下来,让我们观察几种最常见的案例,代入 Prometheus 的第一视角,体会它是如何在条件有限中,做出抉择的。
案例
失真的 rate/increase
在使用 rate 或者 increase 观测 counter 类型的指标增量时,经常碰到以下问题:
- 每分钟新增的请求数,竟然是个小数?
- 不仅是个小数,还比真实增量更大?
- ……
而一种最常见的原因,就是线性外推(linear extrapolation)。
简单粗暴解释:rate/increase[时间范围] 在计算该时间范围内的增量时,第一步要拿到该时间范围边界上(开始时刻和结束时刻)的样本点,相减得到差值。
然而事与愿违的是:在当前时间范围的边界,并不一定那么凑巧地有样本点存在。
此时 Prometheus 的选择是:naive 地假设所有样本点在该时间范围内是均匀分布的,然后按照这个均匀分布的线性规律,“脑补”估算出边界上的采样点。
那么,既然是 “脑补”,“补”出来一些不准确的值,也就不足为奇了。
假设有一个 counter 类型的指标 errors_total ,用于监控业务系统报错的次数。Prometheus 以 15 秒的间隔采样,采集到了如下样本:
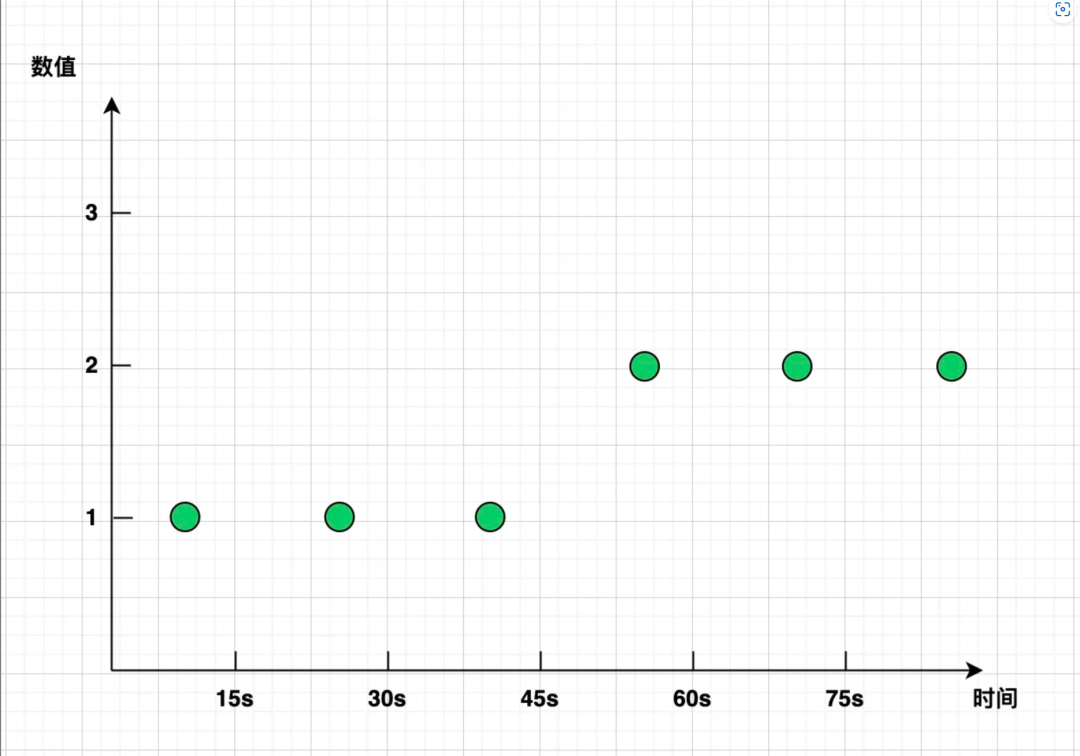
现在需要计算一分钟之内,errors_total 值的增量,也即 increase(errors_total[1m])。(此处为方便起见,仅以 increase 为例。而 rate 本质上是一样的,只是将 increase 在 [时间范围] 内的总增量除以 [时间范围] 的秒数,得到了速率/按秒增量。例如本例中 rate 值就是 increase 值除以 60 秒)。
要计算 [1m] 的时间范围/取样窗口内的 increase,在最理想的情况下,Prometheus 根本不想关心这个窗口内的其他数据,而只需从窗口左边界取第一个点,右边界取最后一个点,相减即可:
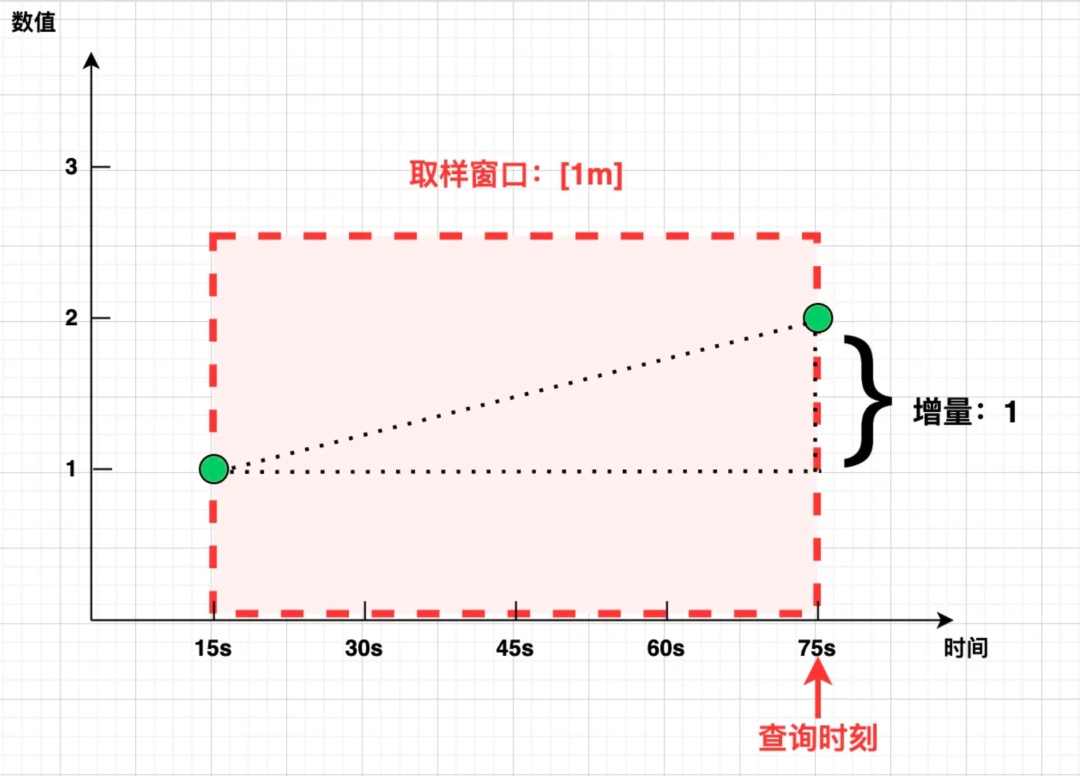
然而在真实的世界中,[1m] 窗口的左右边界却很少能精准“踩中”样本点,而是像下图这样:
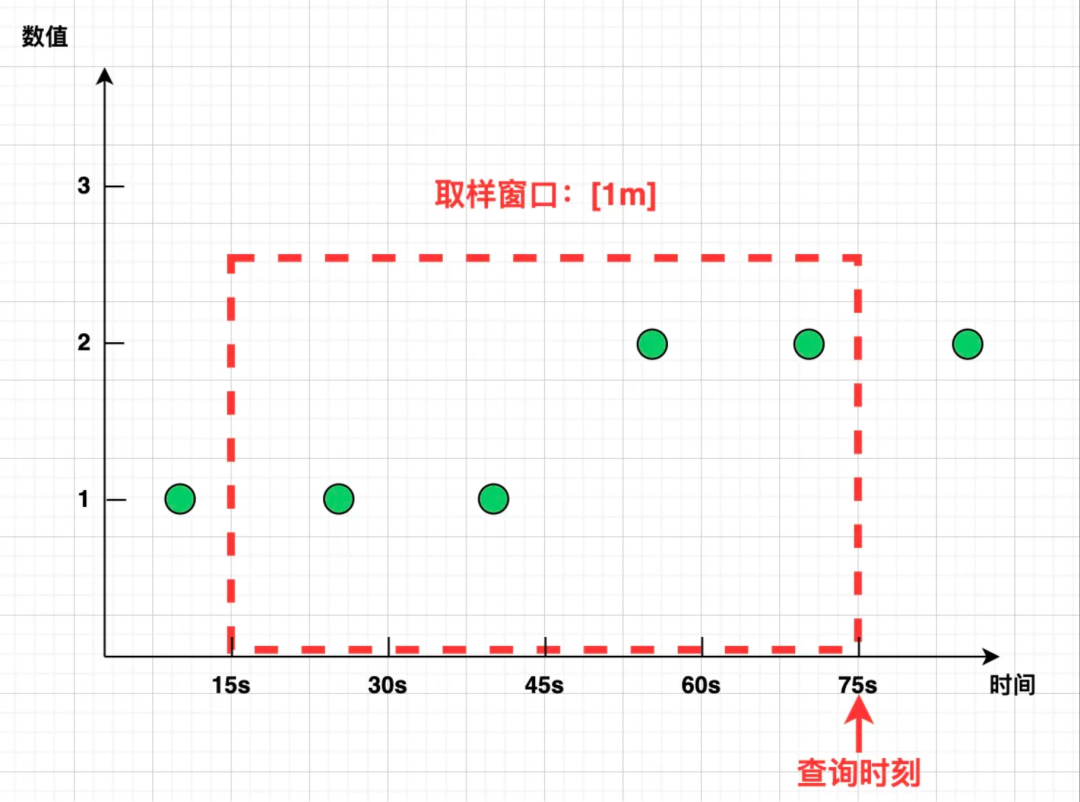
那么问题来了:这 1 分钟的增量该怎么算呢?
Prometheus 选择了一种简易的线性外推算法:取窗口覆盖范围内的第一个点和最后一个点,计算斜率,并按照该斜率将直线延伸至窗口边界,无中生有地“脑补”出虚拟的两个“样本点”,即可相减计算 increase 了:
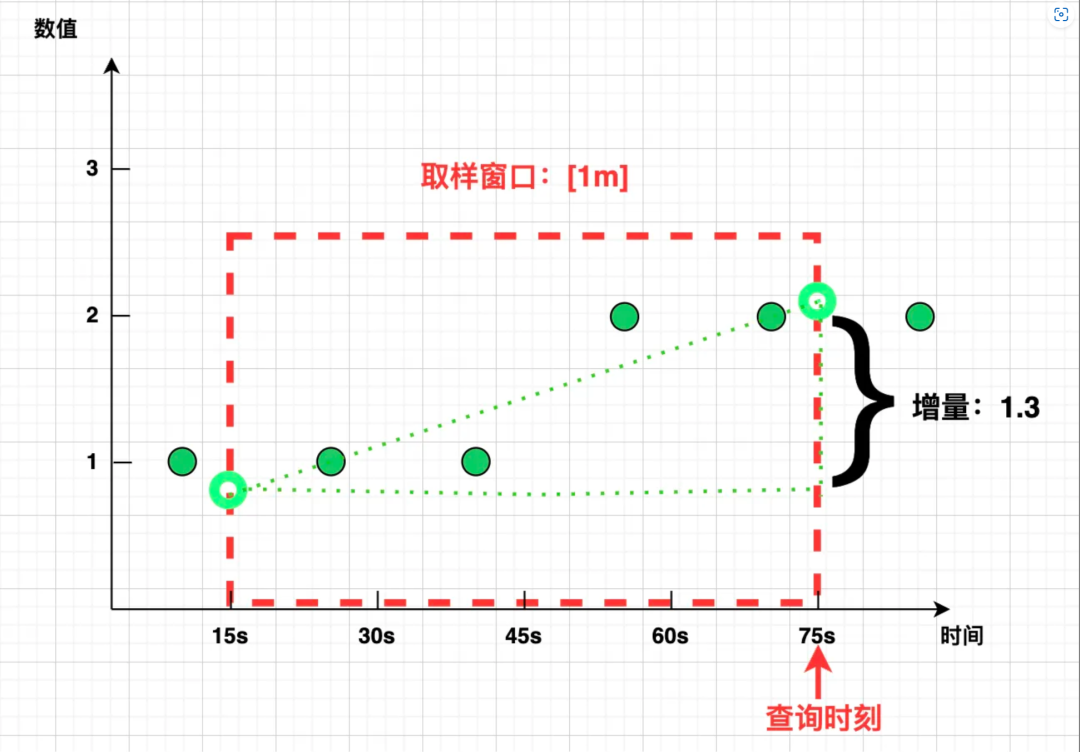
如上所示,用绿圈圈所代表的“虚拟样本”相减,得到的 increase 1.3 不仅是个小数,还比实际值偏大,也就不足为奇了。
离谱的 histogram
每当采集到的样本与 Prometheus 八字不合,P99 往往好似在告诉我们:“在全人类当中,99% 的人月收入少于一万亿。”——没毛病,但也大可不必。
此处就不得不提一个真实历史事件了:我们团队除了有腾讯云 Prometheus,还有个宝藏产品叫 PTS 云压测,能以海量并发向服务端发起请求,来观测服务端在压力下的响应状况。
比如,在压测出来的报告里,与响应时间相关的图表长这样:
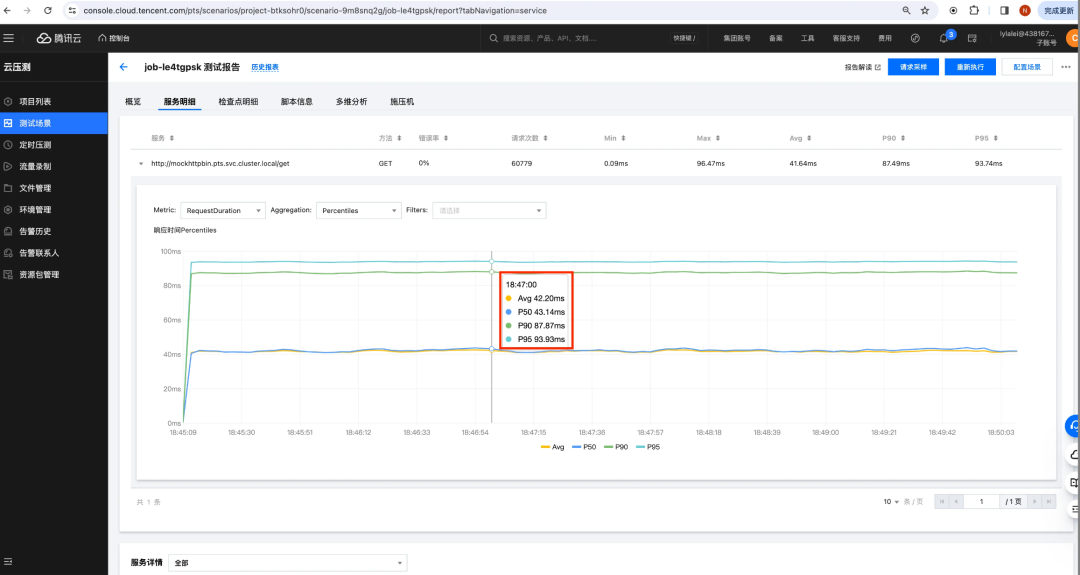
可以看到,PTS 搜集了响应时间的平均值、P50、P90、P95——但就是没有 P99。
其实,最早的时候是有的——毕竟,谁不想用 P99 来做 SLA 啊。
但是,云压测背后的指标存取,还是用的 Prometheus。
于是,在 PTS 还拥有 P99 的那些年,我们三番五次、屡屡破防,最终忍痛拿掉了 P99:

histogram 百分位(percentile)不准,这是为啥呢?这就不得不提线性插值(linear interpolation) 了。
下面以 P99 为例说明(其他百分位也不一定准,但 P99 经常离最大的谱)。
首先,搬运 ChatGPT 老师对 P99 的概念介绍:
P99 是一个统计术语,代表着第99百分位数(99th percentile)。在性能监控和服务质量评估中,P99 常用来衡量响应时间或延迟的指标。具体来说,P99 的含义是在所有测量值中,有 99% 的数据点小于或等于这个值,而只有 1% 的数据点大于这个值。
例如,如果一个网络服务的响应时间的 P99 是 200 毫秒,这意味着在所有的请求中,99% 的请求的响应时间都不会超过 200 毫秒,只有 1% 的请求的响应时间会超过这个数值。这是一个衡量系统在高负载下性能的重要指标,因为它可以告诉你绝大多数用户的体验如何。
简单理解 P99 是怎么得来的:把样本按值的大小依序排队,队伍里第 99% 个样本的值,就是 P99。
那么 Prometheus 在用 histogram 计算 P99 的时候,是否要保存全部哪怕一亿个请求样本的耗时值,才能知道第 99% 的请求所用的时间呢?
显然这不是 Prometheus 的风格。Prometheus 的风格是:宁愿“脑补”,也不愿低效。
于是,跟上面 rate/increase 类似:先从茫茫多的原始数据中采样出样本点,放到各个 bucket(桶)里;然后 naive 地假设所有样本是均匀分布的,据此做线性插值,“无中生有”出所需的“样本点”。
让我们看一个简单案例,模拟每秒产生一个新的 HTTP 请求耗时的观察值,然后计算其 P99。
下面程序为了埋点生成 http_response_time_seconds 这一 histogram 指标,每秒钟暴露一个观察值:
- 有 50% 的概率,样本值大小在 [0.1, 0.5) 范围内。
- 有 50% 的概率,样本值大小在 [0.5, 1.0) 范围内。
package main
import (
"math/rand"
"net/http"
"time"
"github.com/prometheus/client_golang/prometheus"
"github.com/prometheus/client_golang/prometheus/promhttp"
)
var (
httpDuration = prometheus.NewHistogram(prometheus.HistogramOpts{
Name: "http_response_time_seconds",
Help: "HTTP response time distribution",
Buckets: []float64{0.1, 0.5, 100}, // 划分四个桶: <= 0.1、<=0.5、<=100、<=正无穷
})
)
func init() {
prometheus.MustRegister(httpDuration)
}
func main() {
go func() {
for {
// 每秒添加一个新的观察值,是个随机数
// 其值大小有 50% 概率落在 [0.1, 0.5);50% 概率落在 [0.5, 1)
if rand.Float64() < 0.5 {
httpDuration.Observe(rand.Float64()*0.4 + 0.1)
} else {
httpDuration.Observe(rand.Float64()*0.5 + 0.5)
}
time.Sleep(time.Second)
}
}()
http.Handle("/metrics", promhttp.Handler())
http.ListenAndServe(":8080", nil)
}为了卡 Prometheus 的 feature(bug),我们这里划分桶的时候,是相当 naive、相当不合理的:划分四个桶: <= 0.1、<=0.5、<=100、<=正无穷。(对一群不超过 1 的针尖大小的样本值,特地划分一个 0.5 ~ 100 这样宽如黄浦江的 bucket 段,笔者也真是没安好心……)
histogram 的 http_response_time_seconds_bucket 指标是 counter 型,会统计采样到的观察值的样本,落在各个桶内的数量。
还记得我们代码逻辑把一半数值落在 [0.1, 0.5),一半在 [0.5, 1.0) 吗?程序运行一段时间后,将所有样本按值的大小依序排开,观察它们在各个桶内的分布,大致示意如下:
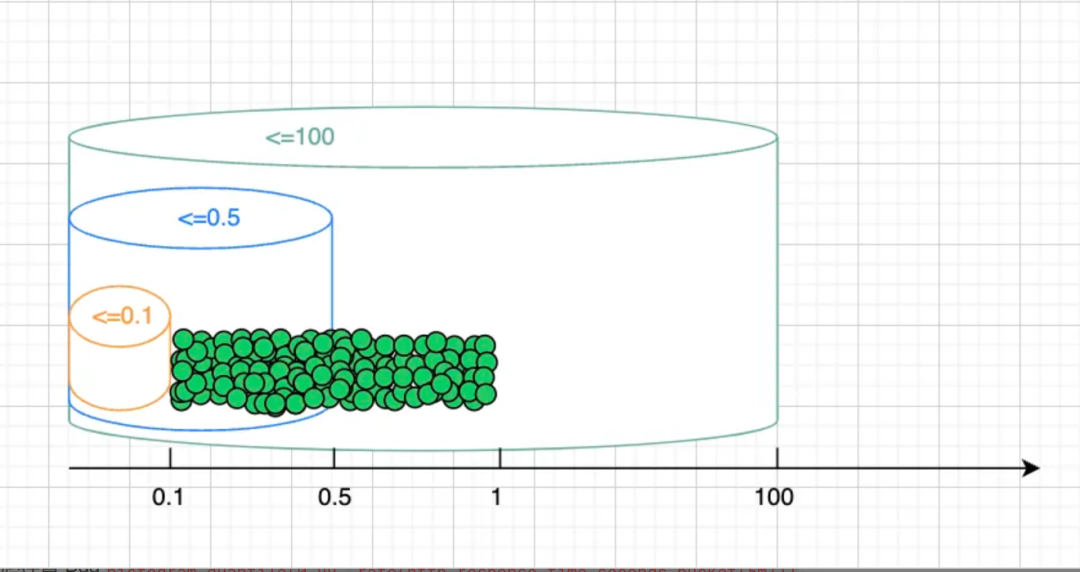
好了,现在要开始计算 P99 histogram_quantile(0.99, rate(http_response_time_seconds_bucket[5m])) 了。
假设现在总共采集到 100 个样本,其中:
- 50% 的样本值大小在 [0.1, 0.5) 范围,那么在 100 个样本中,会有 50 个样本落在 0.1~0.5 bucket 段。
- 50% 的样本值大小在 [0.5, 1) 范围,那么在 100 个样本中,会有 50 个样本会落在 0.5~100 bucket 段。
将样本值从小到大排列,落在 0.1~0.5 bucket 段里的,我们叫它第 1号 ~ 50 号样本;落在 0.5~100 bucket 段里的,我们叫它第 51 号 ~ 第 100号样本。
P99 的计算逻辑如下:
- 根据样本总数和所求分位值,得出目标样本落在第几个 bucket 段:99% 分位 * 总数 100 = 第 99 号。而这第 99 号样本,显然在 0.5~100 bucket 段(因为这个 bucket 段包含第 51 号 ~ 第 100 号样本)。
- 根据本 bucket 段内的样本数和所求分位值,算出目标样本在本 bucket 段内的排行:第 99 号样本在 0.5~100 bucket 段的第 51 号 ~ 第 100 号样本当中,排行 49。
- 根据第 2 步锁定的目标 bucket 段,以及目标样本在该 bucket 段的排行,估算目标样本的值,也即所求分位值。
最终计算分位值公式时,问题就来了。
Prometheus 只知道:
- 有 50 个样本落在 0.5~100 bucket 段。
- 排行第一和排行最末的的样本值之差最大可达 100-0.5(bucket 段的左右边界之差)。
- 目标样本在这个 bucket 段里排行 49。
然而,它并不知道:
- 这个 bucket 段左右边界的差值 100 - 0.5 是否完全分布到了这 50 个样本头上。
- bucket 段内的差值是如何分布到这 50 个样本头上的。
again,Prometheus “脑补” bucket 段内的全额差值,被均匀、线性地,分到了所有样本头上。
因为这样就又可以用线性插值的方式,来计算分位值了:
所求分位值 = bucket 段左边界值 + (bucket 段右边界值 - bucket 段左边界值) * (目标样本在本 bucket 段的排行 / 本 bucket 段的样本总数)。
抛开桶不桶、样本不样本的不谈,在我们的例子中,从目标 bucket 段内求目标样本值的问题,就被简化成了下图所示的形式,直接梦回中学数学课堂,给它一个解:
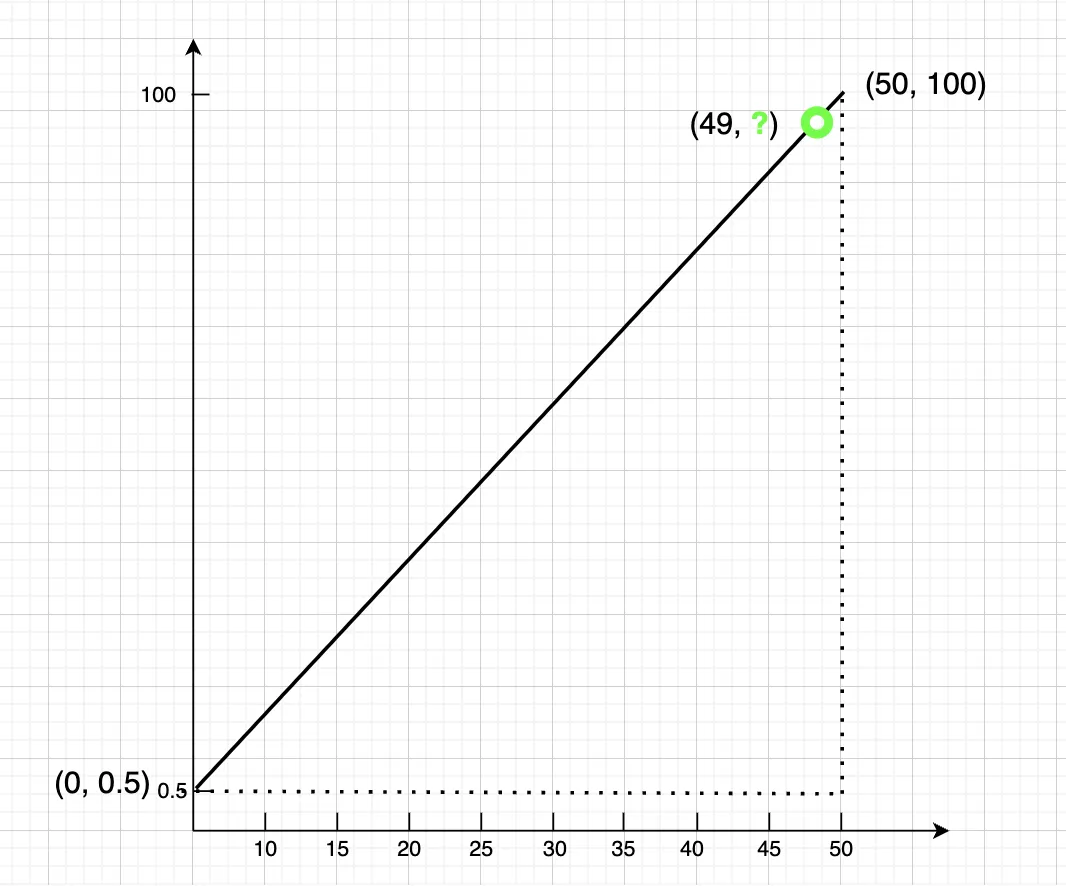
也即:P99 = 0.5 + (100 - 0.5) * (49/50) = 98.01。
给一群不超过 1 的值算出来接近 100 的 P99,其根因也就在于 Prometheus 的“脑补”,与我的桶划分和样本分布,八字不合。
如下图所示:上面的实心绿点代表一群值不超过 1 的真实样本,而由于桶的划分不太合理,导致 Prometheus 线性插值“脑补”出下面那群荧光绿圈,与实际分布偏差很大,最终估算出的 P99 值高达 98+,也就不足为奇了。
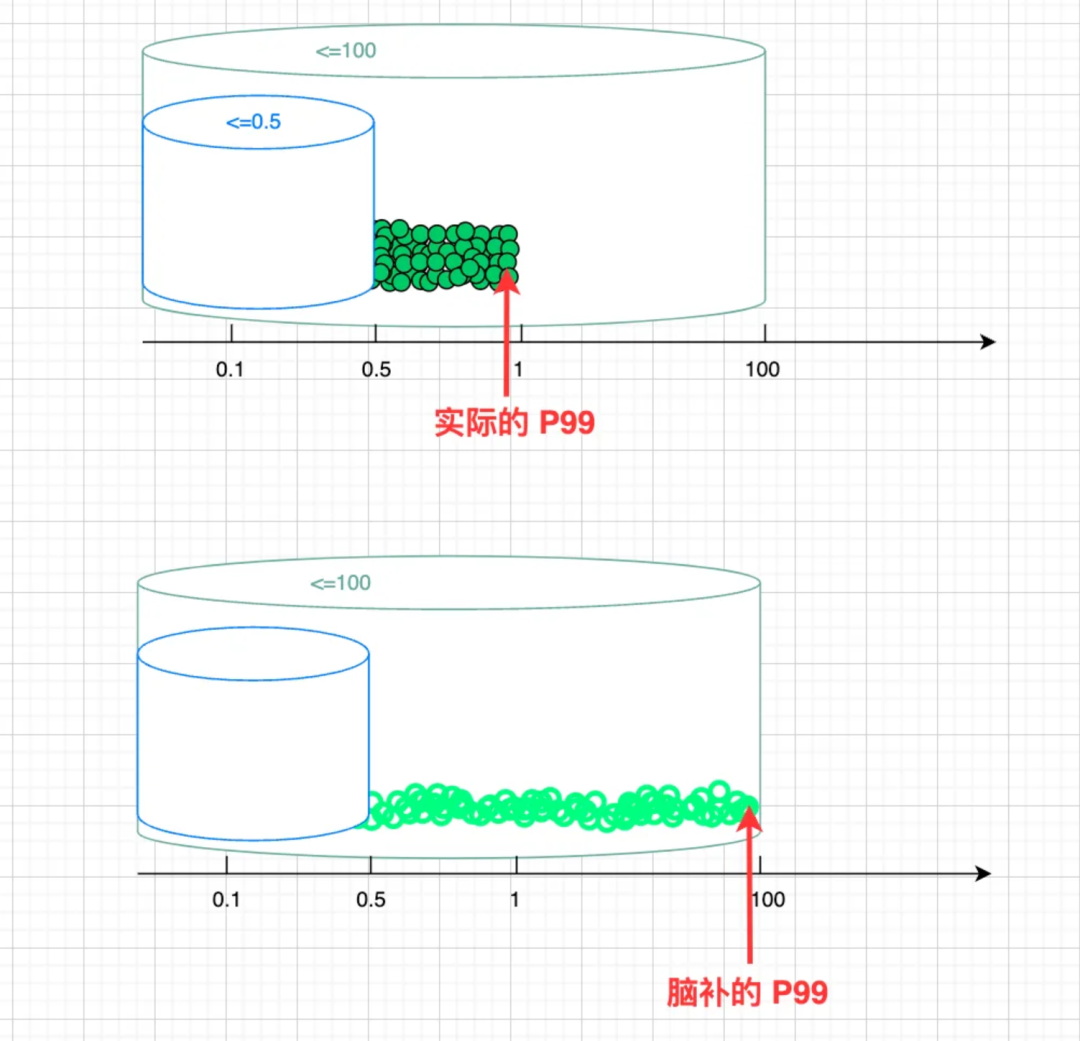
由此可以看出,若想用 histogram 获得较为准确的分位值,则需对样本分布有一定的了解,再根据这个分布,设置合理的 bucket 边界。(PS:若对分位值有较高精度要求、又不了解样本分布、对性能开销和聚合灵活度要求不高,则可考虑使用 summary 代替 histogram。)
薛定谔的 range
当我们选择 rate 的 range 时,我们在选择什么?
仍以上述 rate(errors_total[时间范围]) 为例,若我们分别选时间范围 [30s]、[1m]、[5m],看一眼三者的 Grafana 图表,这不能说一模一样,只能说是毫不相关:随着时间范围扩大,主打一个逐渐平滑、失去尖峰……
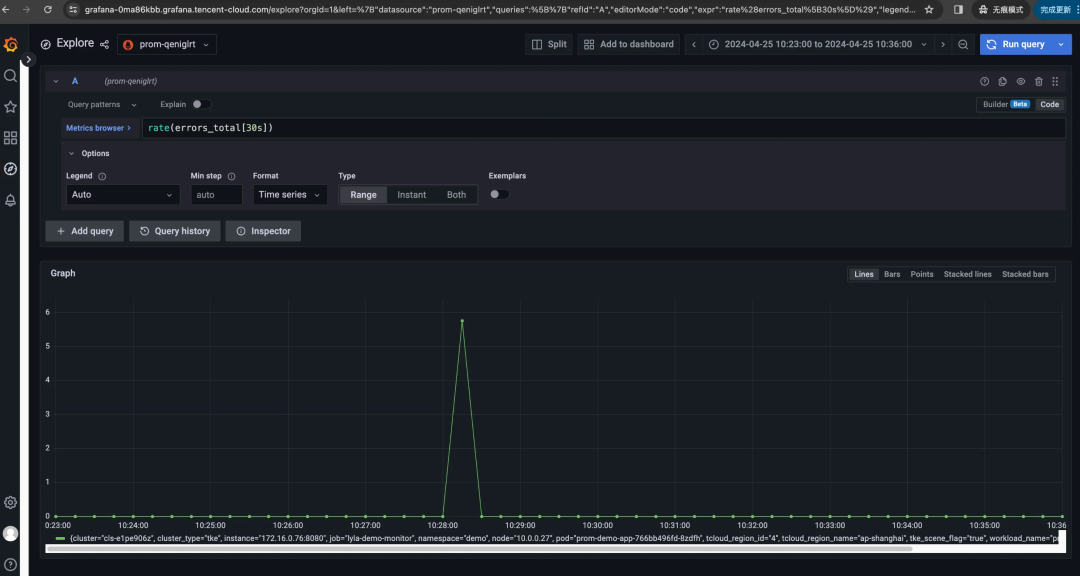
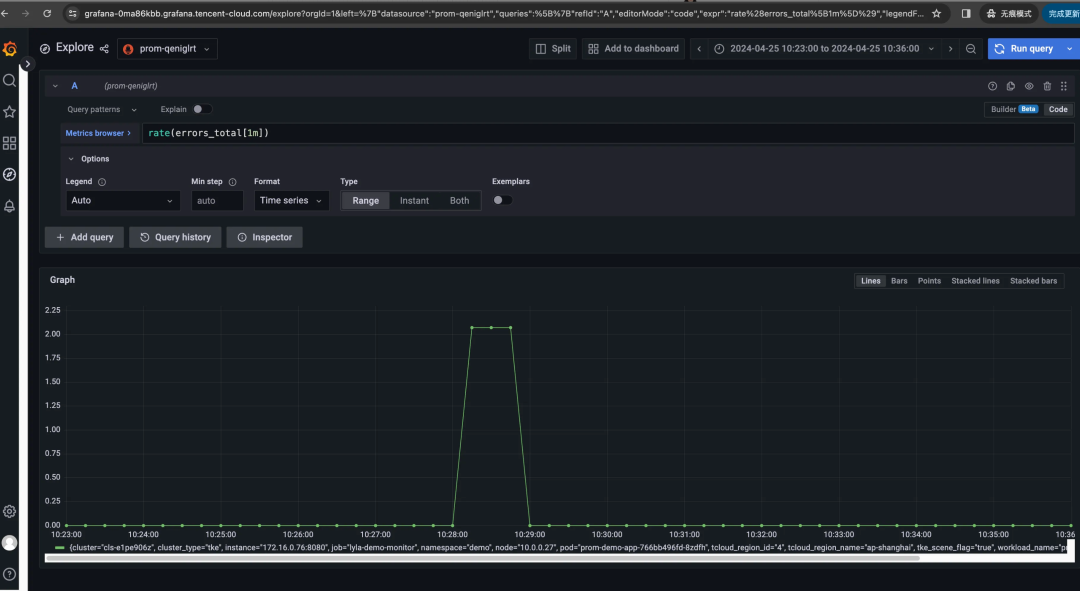
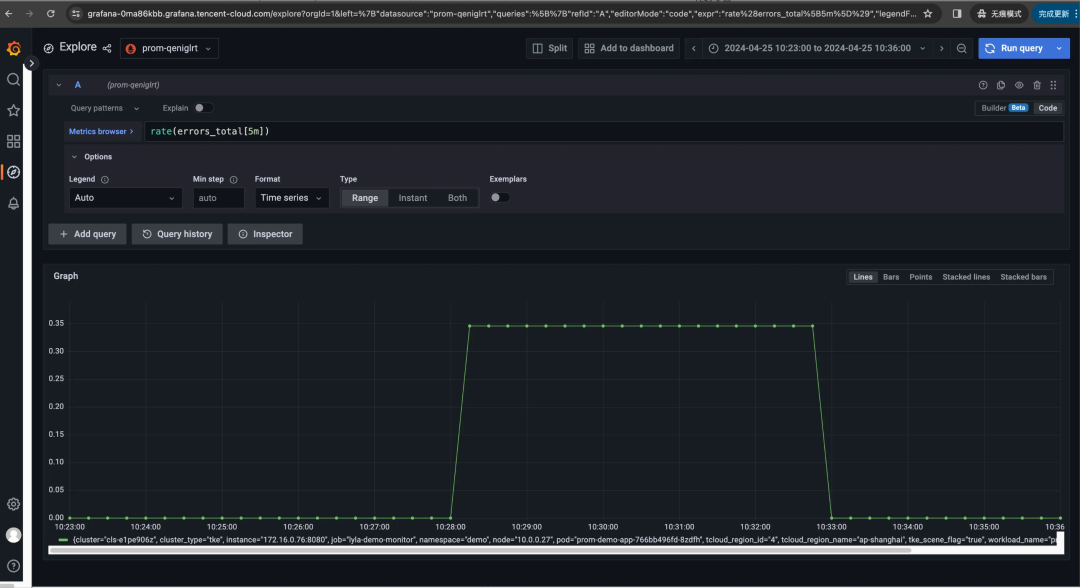
有一说一,rate 不就是速率,速率不就是每秒增量吗?为啥时间范围窗口不同,差异如此之大?区别在于它们计算平均速率的时间窗口不同:
rate[30s]计算过去 30 秒内的平均速率。rate[1m]计算过去 1 分钟内的平均速率。rate[5m]计算过去 5 分钟内的平均速率。
上面这段废话,其实大有深意:同一个尖峰,以不同的形式“被平均”了。
假设我们系统的错误数长期为0,而在某时刻暴增100(如下图日志所示)。
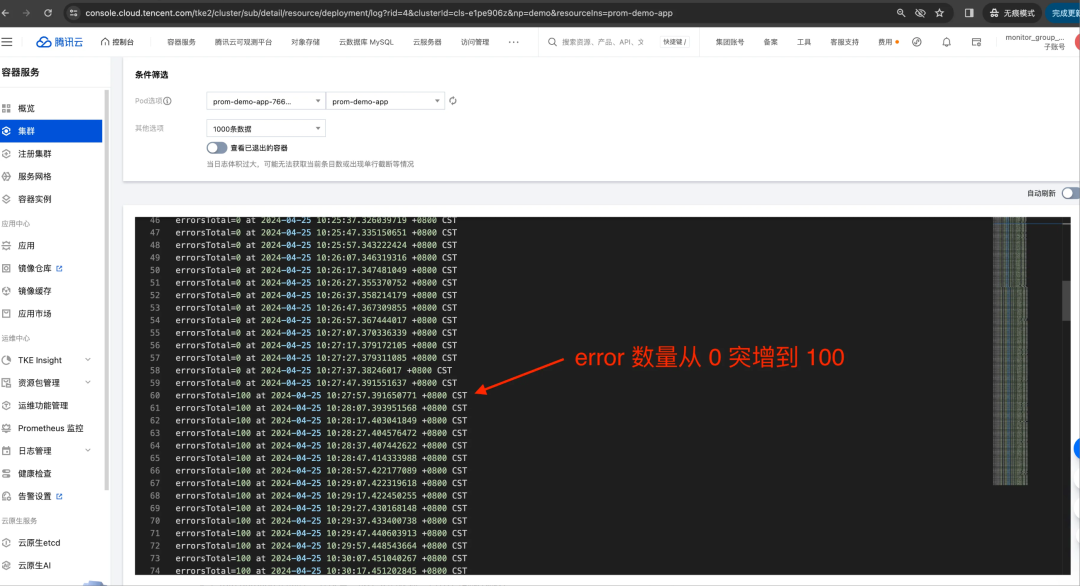
那么上述三种时间范围窗口,意味着将这 100 均分到 30秒,还是 60 秒,还是300秒;那么答案也显而易见:分母越大,按秒平均后的增量则越平滑。
而这就是上述三个 Grafana 曲线随 rate 窗口而峰值和形态大变的原因:
- 窗口小则更加敏感,能够捕捉到更短时间内的变化。这意味着如果有突发事件或者短期波动,它会在曲线上表现得更明显。
- 窗口大会更加平滑,因为它平均了更长时间内的数据。这样可以减少短期波动的影响,但也可能掩盖掉短时间内的突发事件。
关于 rate duration 的选择,并没有一成不变的规则,它并不是越小越好。
选择较小的时间范围可以让你更快地发现问题,但也可能会让你的图表出现很多噪音,特别是在高变化的指标上。
相反,较大的时间范围可以提供更平滑的数据视图,但可能会延迟发现问题。
所以,在选择合适的时间范围时,应考虑以下因素:
- 指标的特性:对于波动较大的指标,可能需要一个较短的时间范围来快速发现问题。对于相对平稳的指标,较长的时间范围可以提供更清晰的趋势。
- 监控目标:如果你需要实时监控和快速响应,短时间范围可能更合适。如果关注长期趋势,那么长时间范围会更有帮助。
- Prometheus 抓取间隔:时间范围应该至少是 Prometheus 抓取间隔的两倍,这样才能确保有足够的数据点来计算速率。
最终,选择合适的时间范围需根据具体情况,进行实验和调整,不断优化这个参数。
结语
以上列举的最典型案例,旨在解释为何 Prometheus 会出现指标值不准的“怪现象”,以及探究它背后的设计原理。
为了言简意赅、去粗存精地解说,上述论述仍然处于最核心、但也经过了简化的场景。
而 Prometheus 在实际使用中的情形,是影响因素更多、也更为复杂的。聊举几例:
- 在一个分布式的世界,网络抖动、对端延迟等引起的数据丢失问题,会给本就不精确的 Prometheus 指标值雪上加霜。 例如:虽则 rate 计算斜率需要至少两个点,但最佳实践建议将 rate 的时间范围至少设为 Prometheus scrape interval(抓取周期/间隔)的 4 倍。这将确保即使抓取速度缓慢、且发生了一次抓取故障,也始终可以使用两个样本。 再例如:网络抖动可能导致丢点,也可能导致点的延迟。那么当延迟的点到达时,它就出现在了本不属于它的统计周期内。这可能导致 rate 出现波动,尤其是在监控较短时间范围的 rate 时。
- 文章里只关注了对 PromQL 的一次查询/evaluation。而在现实中对 Prometheus 使用范围查询(range query),就必然涉及 step(步长)。 比如 Grafana 需要渲染整条曲线,可以理解为 Grafana 在时间轴上按 step 每走一步,就要做一次查询/evaluation,得到一个值,生成曲线上的一个点。那么当 step 的步长,叠加 Prometheus scrape interval,再叠加 PromQL 里的 range 时间范围窗口……可以设想,这几个参数不同的排列组合,会导致曲线更加充满惊喜意外……
- Prometheus 的增量外推(extrapolation),其实也不是纯粹地无脑外推;它有时还会考虑到距离窗口边界的距离,而做一些其他微调。
- 本文未涉及 Prometheus counter 重置(reset)对 increase/rate 准确度的影响。也即:counter 如遇归零(如服务器重启导致),Prometheus 会有应对机制自动来处理,正常情况下不用担心。但若好巧不巧,数据点存在乱序,则可能因为数值下降而误触 Prometheus 重置后的补偿机制,被“脑补”计算出一个极大的异常 increase/rate。
- ……
如此种种,挂一漏万,难以尽述。
总而言之,本文聚焦在最常见、最核心的场景,解析为何 Prometheus 的值不准——而它真的是一个 feature,不是一个 bug。
而围绕着 Prometheus 宇宙,当然有更复杂、更深入的问题亟待探讨。
欲知后事如何,欢迎强势关注腾讯云可观测公众号,以及试用腾讯云可观测平台的 Prometheus 产品。它不仅提供 Prometheus 的原生能力,还能与可观测平台的告警能力强强联合,大大减少您的开发及运维成本。
更多详情欢迎大家微信关注,不仅能限时免费体验产品,还能加入交流群与大佬一起探讨技术。让我们携手不断升级中的腾讯云 Prometheus,一起 stay hungry, stay foolish;持续发掘、持续求索。
