【深度学习】Pytorch教程（八）：PyTorch数据结构：2、张量的数学运算（6）：高维张量：乘法、卷积（conv2d~四维张量；conv3d~五维张量）

Qomolangma

发布于 2024-07-30 11:12:29

59600

代码可运行

文章被收录于专栏：深度学习深度学习

运行总次数：0

代码可运行

一、前言

卷积运算是一种在信号处理、图像处理和神经网络等领域中广泛应用的数学运算。在图像处理和神经网络中，卷积运算可以用来提取特征、模糊图像、边缘检测等。在信号处理中，卷积运算可以用来实现滤波器等操作。

二、实验环境

本系列实验使用如下环境

conda create -n DL python==3.11

conda activate DL

conda install pytorch torchvision torchaudio pytorch-cuda=12.1 -c pytorch -c nvidia

三、PyTorch数据结构

1、Tensor（张量）

Tensor（张量）是PyTorch中用于表示多维数据的主要数据结构，类似于多维数组，可以存储和操作数字数据。

1. 维度（Dimensions）

Tensor（张量）的维度（Dimensions）是指张量的轴数或阶数。在PyTorch中，可以使用size()方法获取张量的维度信息，使用dim()方法获取张量的轴数。

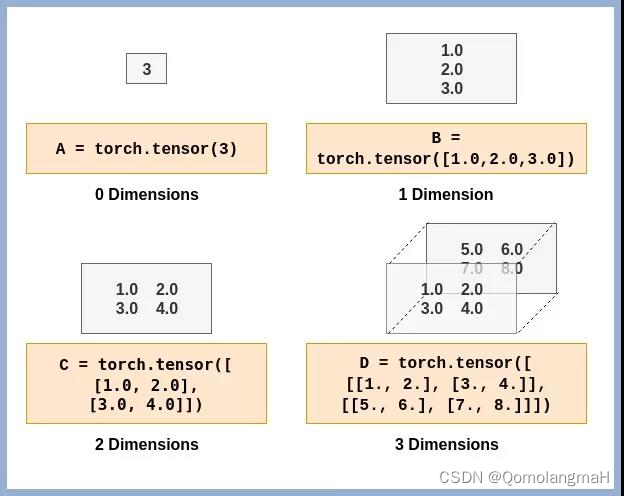
2. 数据类型（Data Types）

PyTorch中的张量可以具有不同的数据类型：

torch.float32或torch.float：32位浮点数张量。
torch.float64或torch.double：64位浮点数张量。
torch.float16或torch.half：16位浮点数张量。
torch.int8：8位整数张量。
torch.int16或torch.short：16位整数张量。
torch.int32或torch.int：32位整数张量。
torch.int64或torch.long：64位整数张量。
torch.bool：布尔张量，存储True或False。

【深度学习】Pytorch 系列教程（一）：PyTorch数据结构：1、Tensor（张量）及其维度（Dimensions）、数据类型（Data Types）

3. GPU加速（GPU Acceleration）

【深度学习】Pytorch 系列教程（二）：PyTorch数据结构：1、Tensor（张量）： GPU加速（GPU Acceleration）

2、张量的数学运算

PyTorch提供了丰富的操作函数，用于对Tensor进行各种操作，如数学运算、统计计算、张量变形、索引和切片等。这些操作函数能够高效地利用GPU进行并行计算，加速模型训练过程。

6. 高维张量

torch.matmul VS torch.mul

torch.matmul：用于执行两个张量的矩阵乘法操作，它要求两个张量的维度需要满足矩阵乘法的规则，例如对于两个三维张量，torch.matmul将在最后两个维度上执行矩阵乘法。

import torch

# 创建两个张量
tensor1 = torch.randn(3, 4) 
tensor2 = torch.randn(4, 5)  

# 矩阵乘法
result = torch.matmul(tensor1, tensor2) 
print(result.shape)

torch.mul：用于对两个张量进行逐元素相乘，即*运算符，会将两个张量的每个元素进行相乘。要求两个张量的形状需要一致或者满足广播规则。
对比

import torch


tensor1 = torch.tensor([[1, 2, 3],
                        [4, 5, 6]])  # shape: (2, 3)

tensor2 = torch.tensor([[7, 8],
                        [9, 10],
                        [11, 12]])  # shape: (3, 2)

# 使用 torch.matmul 进行矩阵乘法
result_matmul = torch.matmul(tensor1, tensor2)  # 结果为 shape (2, 2)
print("Matmul result:")
print(result_matmul)

# 使用 torch.mul 进行逐元素相乘
result_mul = torch.mul(tensor1, tensor2.T)  # 结果为逐元素相乘后的张量
print("\nMul result:")
print(result_mul)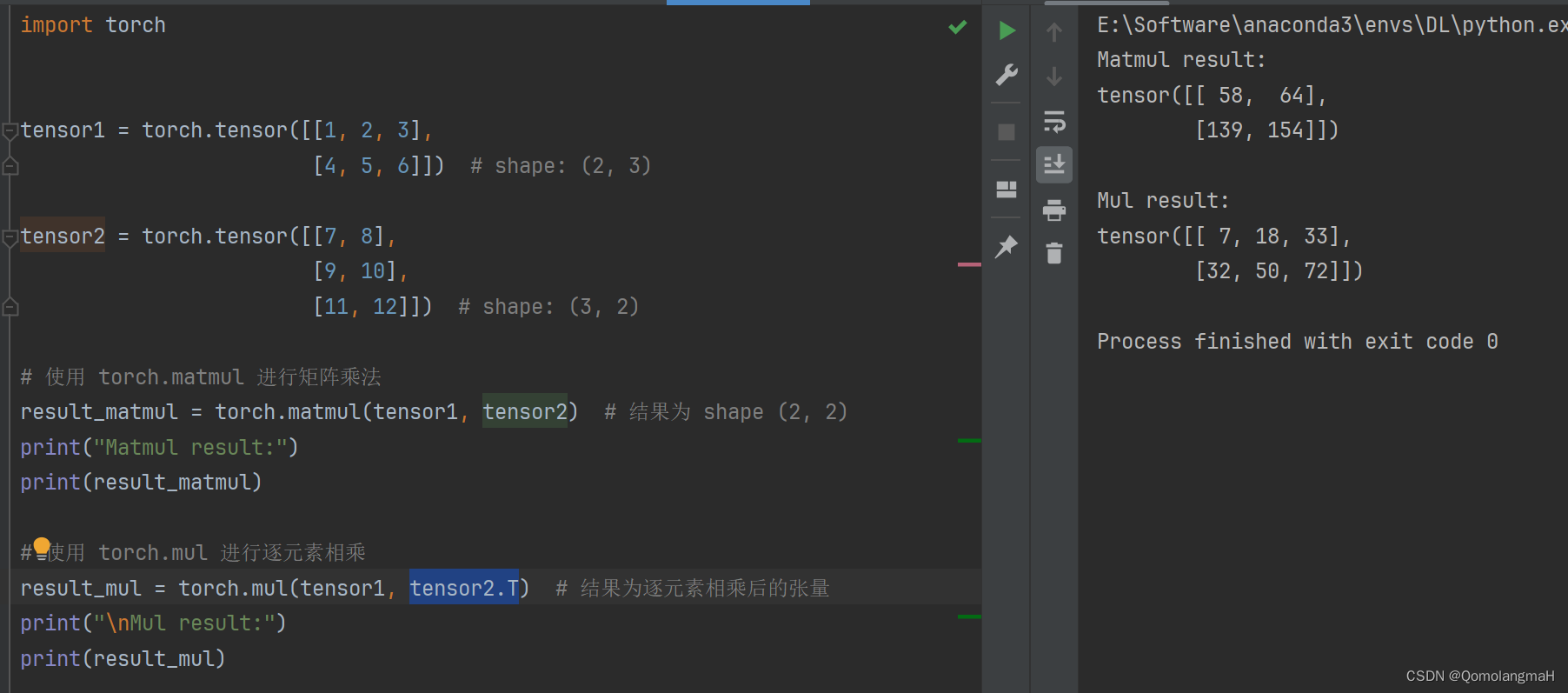

乘法计算原则

张量的维度匹配：两个张量进行乘法操作时，需要保证它们的维度匹配。例如，两个张量的维度分别为（a，b，c）和（c，d），那么它们可以进行乘法操作。
批量乘法：如果两个张量的维度不完全匹配，但它们在最后一维上相符，那么可以进行批量乘法。这意味着两个张量的前面维度需要匹配，并且其中一个张量的维度需要和另一个张量的倒数第二个维度相匹配。

import torch


tensor1 = torch.randn(3, 4, 5)  # 维度为 (3, 4, 5)
tensor2 = torch.randn(3, 5, 6)  # 维度为 (3, 5, 6)
result = torch.matmul(tensor1, tensor2)

print(result.size())  # 输出为 (3, 4, 6)，说明两个张量进行了批量乘法

广播机制：如果两个张量的维度不完全匹配，但是可以通过广播机制进行维度的扩展以匹配，那么可以进行乘法操作。广播机制会自动将维度较小的张量扩展到维度较大的张量上。

import torch


tensor1 = torch.tensor([[1, 2, 3],
                        [4, 5, 6]])  # shape: (2, 3)

tensor2 = torch.tensor([[7, 8],
                        [9, 10],
                        [11, 12]])  # shape: (3, 2)

tensor3 = torch.cat([tensor1, tensor1], dim=1)

# 通过 unsqueeze 添加新的维度来复制成三维张量
# tensor1_3d = tensor1.unsqueeze(0)  # 在第一个维度上添加新的维度
# print(tensor1_3d.shape)  # 输出：(1, 2, 3)
tensor1_3d = tensor1.expand(2, 2, 3)  # 扩展维度
print(tensor1_3d.shape)  # 输出：(2, 2, 3)
print(tensor1_3d)

result_matmul1 = torch.matmul(tensor1, tensor2)
print(f"{tensor1.size()}*{tensor2.size()}={result_matmul1.size()}")
print(result_matmul1)

result_matmul2 = torch.matmul(tensor1_3d, tensor2)
print(f"{tensor1_3d.size()}*{tensor2.size()}={result_matmul2.size()}")
print(result_matmul2)

result_matmul3 = torch.matmul(tensor2, tensor1)
print(f"{tensor2.size()}*{tensor1.size()}={result_matmul3.size()}")
print(result_matmul3)

result_matmul4 = torch.matmul(tensor2, tensor1_3d)
print(f"{tensor2.size()}*{tensor1_3d.size()}={result_matmul4.size()}")
print(result_matmul4)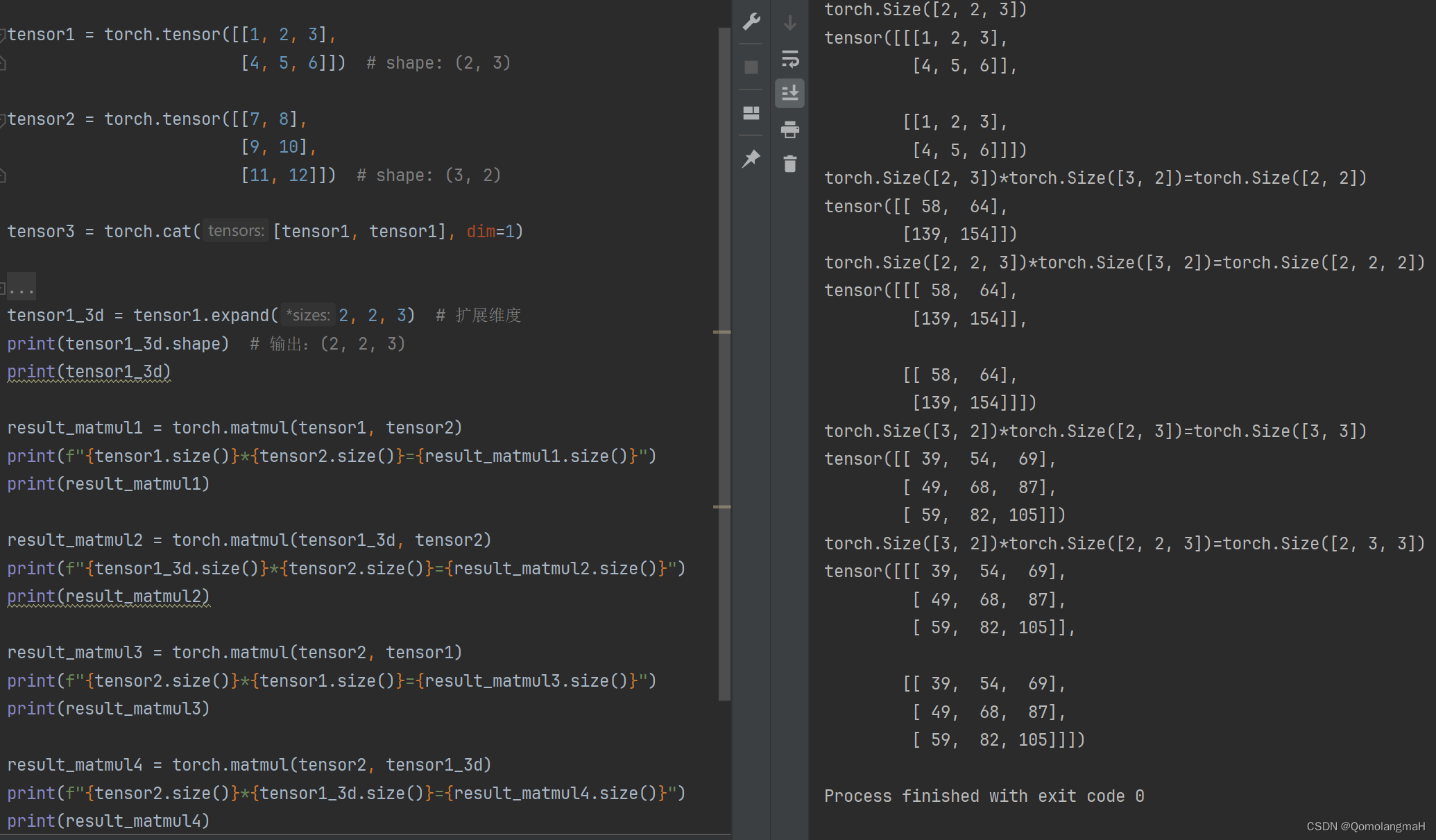

二维卷积conv2d（四维张量）

import torch
import torch.nn.functional as F

# batch_size=2, channel=3, height=32, width=32
input_tensor = torch.randn(2, 3, 32, 32)

# out_channels=4, in_channels=3, kernel_height=3, kernel_width=3
conv_kernel = torch.randn(4, 3, 3, 3)

# 执行卷积操作
output = F.conv2d(input_tensor, conv_kernel, padding=1)

print(output.size())  # 输出为 (2, 4, 32, 32)

通道匹配：卷积核的输入通道数必须与输入张量的通道数相同（

3=3

），这样才能进行逐通道的卷积操作。

大小匹配：卷积核的大小必须小于或等于输入张量的大小（

3<32

），否则无法在输入张量上进行卷积操作。

卷积参数：

- **步长**：卷积时的步长参数需要考虑输入张量的大小；
- **填充**：填充参数可以用来控制卷积操作的输出尺寸，用于保持输入和输出的尺寸一致。

三维卷积conv3d（五维张量）

import torch
import torch.nn.functional as F


#batch_size=2, channel=3, depth=10, height=32, width=32
input_tensor = torch.randn(2, 3, 10, 32, 32)

# out_channels=4, in_channels=3, kernel_depth=3, kernel_height=3, kernel_width=3
conv_kernel = torch.randn(4, 3, 3, 3, 3)
# 执行三维卷积操作
output = F.conv3d(input_tensor, conv_kernel, padding=1)

print(output.size())  # 输出为 (2, 4, 10, 32, 32)

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2024-07-29，如有侵权请联系 cloudcommunity@tencent.com 删除

pytorch